Finite Differenzen Methode
- pDGL wird in Differenzensterne umgewandelt, welche zu algebraischen Gleichungen in den Unbekannten an den Knoten (nicht unbedingt äquidistant) führen
- Ableitungen durch Differenzenausdrücke approximiert
- Taylorreihenentwicklung
- Vorwärts-, Rückwärts-, Zentrale Differenzen bilden
Zeitdiskretisierungsmethoden
Explizites Euler-Verfahren (Euler-Vorwärts-Verfahren):  Implizites Euler-Verfahren (Euler-Rückwärts-Verfahren):
Implizites Euler-Verfahren (Euler-Rückwärts-Verfahren): 
- Vorwärtsdifferenzen
- räumliche Ableitung zum Zeitpunkt n auswerten
- 1. Ordnung genau
- bedingt stabil, zwei Stützstellen
 Implizites Euler-Verfahren (Euler-Rückwärts-Verfahren):
Implizites Euler-Verfahren (Euler-Rückwärts-Verfahren): - Rückwärtsdifferenzen
- räumliche Ableitung zum Zeitpunkt n+1 auswerten
- Gleichungssystem muss für jeden Zeitschritt gelöst werden
- 1. Ordnung genau
- unbeschränkt stabil, zwei Stützstellen

Galerkin-Methode
Gemäß der Galerkin Methode werden die Testfunktionen gleich den Interpolationsfunktionen gesetzt:
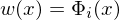
Die Testfunktionen sorgen dafür, dass wir in unserem
Gleichungssystem genügend Gleichungen zur Verfügung haben.
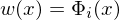
Die Testfunktionen sorgen dafür, dass wir in unserem
Gleichungssystem genügend Gleichungen zur Verfügung haben.
- Qualität der Approximation hängt von Basis- und Testfunktion ab
- Bei Dirichlet-RB treten keine Randterme auf, da
 und
und 
Explizite vs. implizite Methoden
- Explizite Methoden sind einfacher, aber nur bedingt stabil
- Beschränkung der Zeitschrittweite für Euler-Vorwärts Diskretisierung
- Von Neumann Zahl r beschränkt die Ausbreitung in einem Zeitschritt!
- Implizite Methoden stabil, aber erfordern die Lösung eines Matrix-Systems
Gittertypen
Strukturierte Gitter:
Unstrukturierte Gitter: (Verwendung in Realität)
- Regelmäßige Konnektivität: Anzahl benachbarter Knoten konstant
- In 2D ist der zugehörige Elementtyp ein Rechteck
- weniger Speicherbedarf
- Zelldichte schwer anpassbar
- für einfache Gebiete leicht zu erzeugen
Unstrukturierte Gitter: (Verwendung in Realität)
- Unregelmäßige Konnektivität: Anzahl benachbarter Knoten variabel
- In 2D ist der zugehörige Elementtyp z.B. ein Dreieck
- höherer Speicherbedarf
- Zelldichte leicht anpassbar
- gleicher Generierungsaufwand, unabhängig vom Gebiet (automatisch)
Finite-Elemente-Methode
- Das Problem wird in die schwache Form umformuliert
- Generierung des Rechengitters
- Definition der Interpolationsfunktionen
- elementweise Berechnung von Matrizen: Galerkin, Hutfunktion (Interpolationsfunktion)
- Transformation der Integrationsgebiete auf Referenzgebiete
- Assemblierung der Elementmatrizen zur globalen Matrix
- numerische Integration mittels Gaußquadratur
Fehlerarten
Modellierungsfehler:
mathematisches Modell nicht angemessen bzw. zu stark vereinfacht, falsche Annahmen oder ein falsches Modell
Interpolationsfehler:
Diskretisierungsfehler:
mathematisches Modell nicht angemessen bzw. zu stark vereinfacht, falsche Annahmen oder ein falsches Modell
Interpolationsfehler:
- numerische Lösung auf kleine Menge zulässiger Lösungen beschränkt, unzureichende Gitterauflösung
- Differenz zwischen der exakten Lösung und ihrer Interpolante
Diskretisierungsfehler:
- Diskretisierung (FD, FE, FV) kann größere Fehler als den Interpolationsfehler einführen, enthält den Interpolationsfehler
- Diskretisierungsfehler e ist die Differenz zwischen der exakten Lösung und der diskreten Lösung
Interpolationsfehler
- Die Interpolante kann als die beste diskrete Lösung betrachtet werden
- Per Definition ist der Interpolationsfehler an den Knoten Null
- Abhängig von der Gitterschrittweite (je kleiner, desto geringer wird der Interpolationsfehler), Ordnung der Interpolation (höher = besser) (gilt auch für Diskretisierungsfehler)
- Interpolante aus Ansatzfunktionen: stückweise linear, stückweise quadratisch, unstetig stückweise linear, stückweise konstant
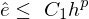
Konsistenz
- Wird die analytische Lösung der Differentialgleichung an den Gitterpunkten ausgewertet und in das diskrete Verfahren eingesetzt, ist die diskrete Gleichung oft nicht erfüllt
- konsistent, wenn diese Abweichung in einer Grenzwertanalyse verschwindet
- diskreter Operator
 nähert sich
nähert sich  mit
mit 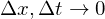

Upwinding
- Verwendung der Rückwärts-Differenzen wird Upwinding genannt: die Ableitung wird nur mit Hilfe der Nachbarwerte stromauf im Sinne der Advektions-Richtung berechnet
- Upwinding fügt dem diskreten System, welches unter den Effekten von negativer numerischer Diffusion leidet, künstliche Diffusion hinzu
Herausforderungen von Advektion
- Advektion stellt eine Herausforderung für numerische Methoden dar
- zentrale Differenzen führen negative numerische Diffusion ein; numerische Lösung zeigt unphysikalische Oszillationen
- Upwinding fügt zu viel künstliche Diffusion hinzu; numerische Lösung zeigt nun unphysikalische Verschmierung
- Optimale Upwinding notwendig bei FD, FE und FV
Zweite Ableitung der Wärmeleitungsgleichung
- die Änderungsrate von T an einem beliebigen Punkt im Stab ist proportional zur zweiten Ortsableitung von T
- Die Proportionalitätskonstante ist eine physikalische Materialeigenschaft und heißt Temperaturleitfähigkeit
- gibt an, wie schnell sich Temperaturänderungen im Stab ausbreiten
Flashcard set info:
Author: CoboCards-User
Main topic: Simulationstechnik RWTH
Topic: CATS
Published: 25.05.2018
Card tags:
All cards (46)
no tags



















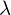 : Wärmeleitfähigkeit
: Wärmeleitfähigkeit