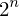Welche Implikationsbeziehungen bestehen zwischen numerischen und reellen Zufallsvariablen?
Jede reelle Zufallsvariable ist auch eine numerische. Die Umkehrung gilt jedoch nicht, denn eine numerische Zufallsvariable, die auch die Werte + ∞ oder − ∞ annehmen kann, ist keine reelle Zufallsvariable.
Tags:
Source: Steyer, Wahrscheinlichkeit und Regression, Kapitel 4, Seite 54f
Source: Steyer, Wahrscheinlichkeit und Regression, Kapitel 4, Seite 54f
Was ist die Kovarianz?
Die Kovarianz zweier Zufallsvariablen X und Y ist ein Kennwert für eine bestimmte Art ihrer stochastischen Abhängigkeit. Sie ist definiert als Erwartungswert der Produktvariablen E([X – E(X)] ⋅ [Y – E(Y)])
Tags:
Source: Steyer, Wahrscheinlichkeit und Regression, Kapitel 5, Seite 71
Source: Steyer, Wahrscheinlichkeit und Regression, Kapitel 5, Seite 71
Der Wahrscheinlichkeitsraum  repräsentiert das bertrachtete Zufallsexperiment. Was sind dabei
repräsentiert das bertrachtete Zufallsexperiment. Was sind dabei  ,
,  und
und 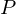 ?
?
 repräsentiert das bertrachtete Zufallsexperiment. Was sind dabei
repräsentiert das bertrachtete Zufallsexperiment. Was sind dabei  ,
,  und
und 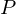 ?
?-
 = Menge der möglichen Ergebnisse
= Menge der möglichen Ergebnisse -
 = Menge der möglichen Ereignisse
= Menge der möglichen Ereignisse 
-
 = ein Wahrscheinlichkeitsmaß auf
= ein Wahrscheinlichkeitsmaß auf 
Tags:
Source: Definitionen.pdf
Source: Definitionen.pdf
Wie berechnet man den t-Wert?

Sichprobenmittelwert
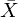
Referenzwert

Schätzer für Standardabweichung

Stichprobengröße

Schätzer für Standardfehler

Tags:
Source: Übung 3_folien, folie 7
Source: Übung 3_folien, folie 7
Tags:
Source: Übung 3_folien, folie 7
Source: Übung 3_folien, folie 7
Wovon wird der Standardfehler des Mittelwertes  beeinflusst?
beeinflusst?
 beeinflusst?
beeinflusst?Der Standardfehler des Mittelwertes  wird beeinflusst von …
wird beeinflusst von …
 wird beeinflusst von …
wird beeinflusst von …- der Standardabweichung der einzelnen Zufallsvariablen in den Stichproben (je größer die Standardabweichung, desto größer der Standardfehler) und
- der Größe der Stichproben (je größer der Stichprobenumfang
 , desto kleiner der Standardfehler).
, desto kleiner der Standardfehler).
Tags:
Source: Übung 3_folien, folie 8
Source: Übung 3_folien, folie 8
Was ist ein Standardfehler des Kennwertes?
Die Standardabweichung der Kennwerteverteilung
(z.B. Standardabweichung der Verteilung der Mittelwerte)
(z.B. Standardabweichung der Verteilung der Mittelwerte)
Tags:
Source: Übung 3_folien, folie 13
Source: Übung 3_folien, folie 13
Welche Entscheidung(sfehler) sind beim Testen möglich?
| in Realität | ||
| Entscheidung |  |  |
 | 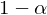 |  , Fehler 2. Art , Fehler 2. Art |
 |  , Fehler 1. Art , Fehler 1. Art |  Teststärke Teststärke |
Tags:
Source: Übung 3_folien, folie 17
Source: Übung 3_folien, folie 17
Was ist eine Prüfverteilung?
Die Verteilung einer Teststatistik unter Gültigkeit der Nullhypothese
nennt man auch eine Prüfverteilung.
(Teststatistik wird als auch Prüfgröße bezeichnet. Anhand der
konkreten Stichprobe wird ein konkreter Wert der Prüfgröße ermittelt)
nennt man auch eine Prüfverteilung.
(Teststatistik wird als auch Prüfgröße bezeichnet. Anhand der
konkreten Stichprobe wird ein konkreter Wert der Prüfgröße ermittelt)
Tags:
Source: Übung 4_folien, folie 3
Source: Übung 4_folien, folie 3
Was ist der  -Wert?
-Wert?
 -Wert?
-Wert?Der  -Wert ist die Wahrscheinlichkeit, dass eine Prüfgröße
-Wert ist die Wahrscheinlichkeit, dass eine Prüfgröße
vorgefunden werden kann, die gleich der ermittelten Prüfgröße oder
extremer als diese ist – vorausgesetzt, die Nullhypothese gilt.
 -Wert ist die Wahrscheinlichkeit, dass eine Prüfgröße
-Wert ist die Wahrscheinlichkeit, dass eine Prüfgröße vorgefunden werden kann, die gleich der ermittelten Prüfgröße oder
extremer als diese ist – vorausgesetzt, die Nullhypothese gilt.
Tags:
Source: Übung 4_folien, folie 3
Source: Übung 4_folien, folie 3
Nenne jeweils ein Beispiel für eine (un)abhändige Stichprobe.
Beispiele für abhängige Stichproben
• Vorher-Nachher-Messung
• Messungen an Paaren (Ehepaare, Geschwisterpaare)
Beispiel für unabhängige Stichproben
• getrennte Gruppen (2 Übungsgruppen ohne „Überschneidung“)
• Vorher-Nachher-Messung
• Messungen an Paaren (Ehepaare, Geschwisterpaare)
Beispiel für unabhängige Stichproben
• getrennte Gruppen (2 Übungsgruppen ohne „Überschneidung“)
Tags:
Source: Übung 4_folien, folie 4
Source: Übung 4_folien, folie 4
Was sind Unterschiede zwischen abhängiger und unabhängiger Stichprobe? Wo finden sich welche?
| abhängige | unabhängige |
 |  |
 |  |
Unterschiede finden sich bei
• Beschreibung des zugrundeliegenden Single-Unit-Trial
• Fragestellung (Bedeutung der µ in den Hypothesen)
• Planung der Untersuchung
• Erhobene Daten (Datensatz)
• Berechung des t-Wertes und der Anzahl der Freiheitsgrade
Tags:
Source: Übung 4_folien, folie 4
Source: Übung 4_folien, folie 4
Was sind Voraussetzungen für einen t-test für abhängige Stichproben?
Voraussetzungen:
- Stichprobe „gepaarter“/abhängiger Zufallsvariablen X1 und X2
- Normalverteilung der Differenzen der Zufallsvariablen und/oder ausreichend große Stichprobe
Tags:
Source: Übung 4_folien, folie 7
Source: Übung 4_folien, folie 7
Was ist die Prüfgröße bei einem t-test für abhängige Stichproben?
Prüfgröße
Differenz bilden

t-Wert:

Differenz bilden

t-Wert:

Tags:
Source: Übung 4_folien, folie 7
Source: Übung 4_folien, folie 7
Prüfverteilung bei einem t-test für abhängige Stichproben?
Prüfverteilung:
t-Verteilung mit
t-Verteilung mit

Tags:
Source: Übung 4_folien, folie 7
Source: Übung 4_folien, folie 7
Was sind die Voraussetzungen um einen t-Test bei einer Stichprobe durchführen zu können?
- Fragestellung: E(X) mit vorgegebenen Wert vergleichen
- EINE Zufallsstichprobe
- Normalverteilung der Zufallsvariablen oder ausreichend große Stichprobe
Tags:
Source: Übung 3_folien, folie 7
Source: Übung 3_folien, folie 7
Was ist eine Zufallsvariable?
- sind Abbildungen

- ordnet jedem Ereignis des betrachteten Zufallsexperiments einen Wert zu
- Werte: Zahlen/Elemente beliebiger Mengen
- Zufallsvariablen haben immer eine Verteilung
Tags:
Source: Steyer
Source: Steyer
Was ist die Verteilung  ?
?
 ?
?- Verteilung
 ist eine Wahrscheinlichkeitsmaß auf
ist eine Wahrscheinlichkeitsmaß auf 

 heißt Verteilung von X
heißt Verteilung von X
Tags:
Source: steyer
Source: steyer
Welche 3 Bedingungen muss eine Sigma-Algebra erfüllen?
-

-

- alle Vereinigungen aller Elemente müssen enthalten sein
Tags:
Source: Steyer, Wahrscheinlichkeit und Regression, Kapitel 2, Seite 31
Source: Steyer, Wahrscheinlichkeit und Regression, Kapitel 2, Seite 31
Was ist die kumulative oder Verteilungsfunktion von X?
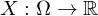 (d.h. reelwertige Zufallsvariablen)
(d.h. reelwertige Zufallsvariablen)Funktion:
 ,
,also die Wahrscheinlichkeit, dafür dass
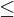 x eintritt
x eintrittTags:
Source: steyer wahrscheinlichkeitstheorie
Source: steyer wahrscheinlichkeitstheorie
Was ist eine diskrete Zufallsvariable?
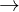 höchstens abzählbar unendliche Menge
höchstens abzählbar unendliche MengeSteyer sagt: Sei X: Ω → Ω′ eine Zufallsvariable auf {Ω, A, P}, dann ist die Menge X(Ω) der Werte von X höchstens abzählbar unendlich, so heißt X diskret.
Im diskreten Fall enthält die Verteilung der diskreten Zufallsvariable auch die Wahrscheinlichkeiten P(X = x), dass die betrachtete Zufallsvariable jeweils einen bestimmten Wert x annimmt.
Tags:
Source: steyer
Source: steyer
Was ist ein Faktor/eine Stufe bei der ANOVA?
Faktor: unabhängige Variable
Stufe: Ausprägungen des Faktors
Stufe: Ausprägungen des Faktors
Tags:
Source: Übung 5_folien, folie 9
Source: Übung 5_folien, folie 9
Was sind Vorraussetzungen für eine ANOVA?
- Mehrere unabhängige Stichproben
- Varianzhomogenität
- Normalverteilung und/oder ausreichend große Stichprobe
- Varianzhomogenität
- Normalverteilung und/oder ausreichend große Stichprobe
Tags:
Source: Ü5, Folie 9
Source: Ü5, Folie 9
Was sind die Vorraussetzungen für einen t-Test für unabhängige Stichproben?
Voraussetzungen:
- 2 unabhängige Stichproben mit den Umfängen
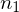 und
und 
- Varianzhomogenität

- Normalverteilung der Zufallsvariablen und/oder ausreichend große Stichprobe
Tags:
Source: Übung 4_folien, folie 12
Source: Übung 4_folien, folie 12
Was ist die Prüfgröße für eine t-test für unabhängige Stichproben?
t-Wert:
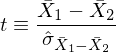
 Zufallsvariable X der Gruppe 1
Zufallsvariable X der Gruppe 1
 Zufallsvariable X der Gruppe 2
Zufallsvariable X der Gruppe 2
 Schätzer für die Standardabweichung
Schätzer für die Standardabweichung
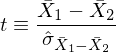
 Zufallsvariable X der Gruppe 1
Zufallsvariable X der Gruppe 1 Zufallsvariable X der Gruppe 2
Zufallsvariable X der Gruppe 2 Schätzer für die Standardabweichung
Schätzer für die StandardabweichungTags:
Source: Übung 4_folien, folie 12
Source: Übung 4_folien, folie 12
Was ist die Prüfverteilung für eine t-test für unabhängige Stichproben
t-Verteilung mit


Tags:
Source: Übung 4_folien, folie 12
Source: Übung 4_folien, folie 12
Wie wird bei einem t-test für unabhängige Stichproben die Varianzhomogenität geprüft? Was wird gemacht, wenn keine Varianzhomogenität vorliegt?
Beim t-Test für unabhängige Stichproben wird angenommen, dass
gleiche Varianzen in den verschiedenen Gruppen vorliegen.
gleiche Varianzen in den verschiedenen Gruppen vorliegen.
- Die Nullhypothese
 wird in SPSS (automatisch) mit dem Levene-Test geprüft
wird in SPSS (automatisch) mit dem Levene-Test geprüft - Kann beim Levene-Test die Nullhypothese verworfen werden, dann wird für den Gruppenvergleich der Welch-Test verwendet. Standardfehler und Freiheitsgrade werden dann anders berechnet.
- Die Ergebnisse des Welch-Tests befinden sich im SPSS-Output in der 2. Zeile der Tabelle „Test bei unabhängigen Stichproben“
Tags:
Source: Übung 4_folien, folie 13
Source: Übung 4_folien, folie 13
Tags:
Source: Übung 4_folien, folie 7
Source: Übung 4_folien, folie 7
Warum macht man bei dem Vergleich mehreren Gruppen eine Varianzanalyse statt t-test's?
- mit t-Test nur Vergleich von zwei Gruppenmittelwerten möglich
- man könnte bei drei und mehr Gruppen mehrere t-Tests durchführen → „α-Fehler-Inflation“ → α-Niveau adjustieren
Tags:
Source: Übung 5_folien, folie 5
Source: Übung 5_folien, folie 5
Was ist das Ziel einer Analysis of Variance (ANOVA)?
- Gleichen sich die Erwartungswerte (von Y) bei mehreren Gruppen? Oder gibt es Unterschiede?
- insbesondere wenn mehr als zwei Gruppen verglichen werden
Tags:
Source: Übung 5_folien, folie 6
Source: Übung 5_folien, folie 6
Tags:
Source: steyer
Source: steyer
Welche Varianten des  -test gibt es?
-test gibt es?
 -test gibt es?
-test gibt es?- Vergleich der Verteilungen einer ZV mit einer vorgegebenen Verteilung (z.B. der Gleichverteilung)
- Vergleich zweier diskreter ZV (z.B. Prüfen von stochastischer Unabhängigkeit zweier dichotomer Zufallsvariablen)
- zur Modellgeltungskontrolle in der Testtheorie (4. Semester)
Tags:
Source: Ü6 Folie 5
Source: Ü6 Folie 5
Was sind die Vorraussetzungen für einen  -test auf Gleichverteilung?
-test auf Gleichverteilung?
 -test auf Gleichverteilung?
-test auf Gleichverteilung?- Eindeutige Zuordnung zu den Kategorien
- Ausreichend große Stichprobe (erwartete absolute Häufigkeiten in jeder Zelle sind mindestens 5, bei 2 Gruppen mindestens 10)
Tags:
Source: Ü6 Folie 9
Source: Ü6 Folie 9
Wie wird X²-Test auf Gleichverteilung berechnet?
1. Berechne die erwarteten Häufigkeiten unter der  mit Hilfe von
mit Hilfe von
– Vorwissen (Anzahl der Gruppen)
– Angaben aus den Daten (Stichprobengröße) und
– Annahmen aus der Nullhypothese (Gleichverteilung)
2 . Berechne X²-Wert.
Hinweis: Je stärker erwartete und beobachtete Häufigkeiten abweichen, desto größer wird der berechnete X²-Wert und umso eher wird der Test signifikant.
 mit Hilfe von
mit Hilfe von – Vorwissen (Anzahl der Gruppen)
– Angaben aus den Daten (Stichprobengröße) und
– Annahmen aus der Nullhypothese (Gleichverteilung)
2 . Berechne X²-Wert.
Hinweis: Je stärker erwartete und beobachtete Häufigkeiten abweichen, desto größer wird der berechnete X²-Wert und umso eher wird der Test signifikant.
Tags:
Source: Ü6 f11
Source: Ü6 f11
Was ist ein Erwartungswert?
Ein Kennwert einer Verteilung von Zufallsvariablen
Der Mittelwert ist ein empirischer Schätzer des Erwartungswertes
der wahre mittelwert
Der Mittelwert ist ein empirischer Schätzer des Erwartungswertes
der wahre mittelwert
Tags:
Source: Ü1f24
Source: Ü1f24
Tags:
Source: Steyer
Source: Steyer
Wie wird eine Korrelation (Corr (X,Y)) berechnet?
die Kovarianzen von X, Y difidiert durch das Produkt der SD's

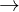 SD's müssen positiv sein
SD's müssen positiv sein

für SD(X), SD(Y) > 0

 SD's müssen positiv sein
SD's müssen positiv sein 
für SD(X), SD(Y) > 0
Tags:
Source: Steyer
Source: Steyer
Welcher Zusammenhang besteht zwischen dem Signifikanzniveau,  und
und  Fehler ?
Fehler ?
 und
und  Fehler ?
Fehler ? Signifikanzniveau gibt die Whk an, einen  Fehler zu begehen, falls die
Fehler zu begehen, falls die  gilt.
gilt.
einen deterministischen Zh zw Signifikanzniveau und Fehler gibt es nicht, aber es gilt, je kleiner der
Fehler gibt es nicht, aber es gilt, je kleiner der  Fehler, desto größer der
Fehler, desto größer der  Fehler, wenn alles andere konstant bleibt.
Fehler, wenn alles andere konstant bleibt.
 Fehler zu begehen, falls die
Fehler zu begehen, falls die  gilt.
gilt. einen deterministischen Zh zw Signifikanzniveau und
 Fehler gibt es nicht, aber es gilt, je kleiner der
Fehler gibt es nicht, aber es gilt, je kleiner der  Fehler, desto größer der
Fehler, desto größer der  Fehler, wenn alles andere konstant bleibt.
Fehler, wenn alles andere konstant bleibt.Tags:
Source: Übungszettel 4, seite 3
Source: Übungszettel 4, seite 3
Was ist ein Standardfehler?
(a) Die Streuung der einzelnen Messwerte einer Stichprobe.
(b) Die Streuung der Messwerte um die Regressionsgerade.
(c) Die Standardabweichung der Stichprobenkennwerte.
(d) Ein theoretischer Wert, dessen Schätzung je nach Stichprobe schwanken kann.
(a) Die Streuung der einzelnen Messwerte einer Stichprobe.
(b) Die Streuung der Messwerte um die Regressionsgerade.
(c) Die Standardabweichung der Stichprobenkennwerte.
(d) Ein theoretischer Wert, dessen Schätzung je nach Stichprobe schwanken kann.
c,d
Tags:
Source: Übungszettel 6, seite 1
Source: Übungszettel 6, seite 1
Wie berechnet sich die Teststärke?

(ist also die Power des Test die
 zu erkennen und die
zu erkennen und die  exakterweise zu verwerfen)
exakterweise zu verwerfen)Tags:
Source: Ü3f17
Source: Ü3f17
Wann ist ein Schätzer erwartungstreu?
Wenn der Erwartungswert des Schätzer dem wahren Wert entspricht.
Tags:
Source: Ü7f11
Source: Ü7f11
Der  -Wert ist...
-Wert ist...
 -Wert ist...
-Wert ist...die Wahrscheinlichkeit, dass ein Wert auftritt, der gleich der ermittelnden Prüfgröße oder extremer als diese ist - vorrausgesetzt die  gilt
gilt
 gilt
giltTags:
Source: Ü7f11
Source: Ü7f11
Welche Faktoren beeinflussen den β-Fehler? Wie?
- stichprobengröße, je größer, desto kleiner β-Fehler
- standardabweichung, je größer, desto größer β-Fehler
- Alphaniveau, je niedriger, desto größer β-Fehler
- true difference
Tags:
Source: Ü7f11
Source: Ü7f11
 verwendet man beim t-Test für...
verwendet man beim t-Test für...abhängige Stichproben
(bspw. die Differenz der Zufallsvariablen zu zwei Messzeitpunkten)
(bspw. die Differenz der Zufallsvariablen zu zwei Messzeitpunkten)
Tags:
Source: Ü7f14
Source: Ü7f14
Die Gleichungen für die Berechnung der Prüfgröße ähneln sich bei allen vorgestellten Varianten des t-Test. Was wird durch was geteilt?
Mittelwerstdifferenz durch den Schätzer für den Standardfehler (Standabweichung durch die Wurzel aus  )
)
 )
)Tags:
Source: Ü7f14
Source: Ü7f14
Die Prüfgröße bei der ANOVA ist...
die Varianz zwischen geteilt durch die Varianz innerhalb der Gruppen.
Tags:
Source: Ü11f16
Source: Ü11f16
Die „Varianz zwischen“ ist (bei der ANOVA)...
die gewichtete Summe der Abweichungsquadrate von Gruppenmittelwerten und Gesamtmittelwert geteilt durch df (= p-1)
Tags:
Source: Ü7f16
Source: Ü7f16
Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Tags:
Source: Übungszettel 4, seite 2
Source: Übungszettel 4, seite 2
Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Tags:
Source: Übungszettel 4, seite 2
Source: Übungszettel 4, seite 2
Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Tags:
Source: Übungszettel 4, seite 2
Source: Übungszettel 4, seite 2
Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Tags:
Source: Übungszettel 4, seite 2
Source: Übungszettel 4, seite 2
Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Tags:
Source: Übungszettel 4, seite 2
Source: Übungszettel 4, seite 2
Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Tags:
Source: Übungszettel 4, seite 2
Source: Übungszettel 4, seite 2
Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Tags:
Source: Übungszettel 4, seite 2
Source: Übungszettel 4, seite 2
Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Tags:
Source: Übungszettel 4, seite 2
Source: Übungszettel 4, seite 2
Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Tags:
Source: Übungszettel 4, seite 2
Source: Übungszettel 4, seite 2
Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Tags:
Source: Übungszettel 4, seite 2
Source: Übungszettel 4, seite 2
Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Tags:
Source: Übungszettel 4, seite 2
Source: Übungszettel 4, seite 2
Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Tags:
Source: Übungszettel 4, seite 2
Source: Übungszettel 4, seite 2
Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Tags:
Source: Übungszettel 4, seite 2
Source: Übungszettel 4, seite 2
Was ist ein 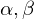 -Fehler?
-Fehler?
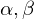 -Fehler?
-Fehler?
wenn die
 verworfen wird, obwohl sie in Realität zutrifft
verworfen wird, obwohl sie in Realität zutrifft
wenn die
 beibehalten wird, obwohl die
beibehalten wird, obwohl die  in Realität zutrifft
in Realität zutrifftTags:
Source: Übung/steyer
Source: Übung/steyer
Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Tags:
Source: Übungaszettel 4, seite 3
Source: Übungaszettel 4, seite 3
Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Tags:
Source: Übungaszettel 4, seite 3
Source: Übungaszettel 4, seite 3
Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Tags:
Source: Übungaszettel 4, seite 3
Source: Übungaszettel 4, seite 3
Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Tags:
Source: Übungaszettel 4, seite 3
Source: Übungaszettel 4, seite 3
Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Tags:
Source: Übungaszettel 4, seite 3
Source: Übungaszettel 4, seite 3
Welcher Zusammenhang besteht zwischen einerseits dem Signi
kanzniveau und andererseits dem  - und
- und
 -Fehler?
-Fehler?
 - und
- und -Fehler?
-Fehler?Bei statstischen Test wird im Vorab das Signi
kanzniveau festgelegt. Es gibt die Wahrscheinlichkeit an, einen  -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt.
Einen deterministischen Zh zw Signifikanzniveau und -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.
 -Fehler zu begehen, falls die
-Fehler zu begehen, falls die  gilt.
gilt. Einen deterministischen Zh zw Signifikanzniveau und
 -Fehler gibt es nicht. Es gilt aber, je kleiner der
-Fehler gibt es nicht. Es gilt aber, je kleiner der  -Fehler, desto größer der
-Fehler, desto größer der  -Fehler wenn alle anderen Bedingungen konstant gehalten werden.
-Fehler wenn alle anderen Bedingungen konstant gehalten werden.Tags:
Source: Übungaszettel 4, seite 3
Source: Übungaszettel 4, seite 3
Tags:
Source: Steyer 2011-04-07_folien.pdf, folie 16
Source: Steyer 2011-04-07_folien.pdf, folie 16
Welches Testverfahren verwendet man für (mehr als) 2 Stichproben?
2 Stichproben: t-test
>2 Stichproben: ANOVA
>2 Stichproben: ANOVA
Tags:
Source: Übung 1_folien, folie 18
Source: Übung 1_folien, folie 18
Welche Teststatistik wird bei einem t-Tests, ANOVA, X²-Vierfelder-Test verwendet?
- t-Wert (t-Tests)
- f-Wert (ANOVA)
- X²-Wert (X²-Vierfelder-Test)
Tags:
Source: Übung 1_Folien, Folie 20
Source: Übung 1_Folien, Folie 20
Tags:
Source: Übung 1_Folien, Folie 21
Source: Übung 1_Folien, Folie 21
Tags:
Source: Übung 1_Folien, Folie 24
Source: Übung 1_Folien, Folie 24
Tags:
Source: Übung 1, Folie 25
Source: Übung 1, Folie 25
Was ist eine Teststatistik?
Synonym: Prüfgröße
Praktisch: Ein Wert, der aus den Stichprobendaten berechnet wird und die Grundlage für eine statistische Entscheidung bildet
Theoretisch: Eine Zufallsvariable, deren Verteilung unter bestimmten Annahmen bekannt ist Prüfgröße hat eine Verteilung
Prüfgröße hat eine Verteilung
Praktisch: Ein Wert, der aus den Stichprobendaten berechnet wird und die Grundlage für eine statistische Entscheidung bildet
Theoretisch: Eine Zufallsvariable, deren Verteilung unter bestimmten Annahmen bekannt ist
 Prüfgröße hat eine Verteilung
Prüfgröße hat eine VerteilungTags:
Source: Übung 1, Folie 28
Source: Übung 1, Folie 28
Welche Kennwerte hat die Standard-Normalverteilung?
E(X) = 0

Zudem:
X-Achse: Ausprägung der ZV, Y-Achse: Dichte

Zudem:
X-Achse: Ausprägung der ZV, Y-Achse: Dichte
Tags:
Source: Übung 1, Folie 30
Source: Übung 1, Folie 30
Wie lautet der Faktorisierungssatz?
Wenn P(A1)> 0, dann gilt:
P(A1 ∩ A2) = P(A1)*P(A2 | A1)
Wenn P(A1 ∩. . .∩ An−1) > 0, dann gilt:
P(A1 ∩ . . . ∩ An) =
P(A1)*P(A2 | A1)*P(A3 | A1 ∩ A2) *. . . *P(An | A1 ∩ . . . ∩ An−1)
Tags:
Source: Steyer 2011-04-07_folien.pdf
Source: Steyer 2011-04-07_folien.pdf
Was ist das zweite Axiom von Kolmogoroff?
- wenn
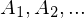 eine Folge paarweise disjunkter Mengen
eine Folge paarweise disjunkter Mengen  ist
ist - dann gilt:

Tags:
Source: Definitionen.pdf
Source: Definitionen.pdf
Tags:
Source: http://de.wikipedia.org/wiki/Datei:Venn0111.svg
Source: http://de.wikipedia.org/wiki/Datei:Venn0111.svg
Flashcard set info:
Author: Finn
Main topic: Statistik
School / Univ.: Friedrich-Schiller-Universität
City: Jena
Published: 14.09.2011
Card tags:
All cards (94)
no tags




 ?
?


 = Schätzer für die Standardabweichung
= Schätzer für die Standardabweichung



 berechnet?
berechnet? 

 stochastische unabhängig?
stochastische unabhängig? ,
,



 = relative Häufigkeit
= relative Häufigkeit  ?
?
 , für alle
, für alle 

 ausgesprochen?
ausgesprochen? ausgesprochen?
ausgesprochen?
 ausgesprochen?
ausgesprochen?
 ausgesprochen?
ausgesprochen?