Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
11
Def.: kompakt
Die Menge  heißt (folgen-)kompakt, wenn jede Folge aus
heißt (folgen-)kompakt, wenn jede Folge aus  eine konvergente Teilfolge mit Grenzwert in
eine konvergente Teilfolge mit Grenzwert in  besitzt.
besitzt.
Jede kompakte Menge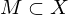 ist beschränkt und abgeschlossen bezüglich der Metrik
ist beschränkt und abgeschlossen bezüglich der Metrik 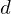 von
von 
 heißt (folgen-)kompakt, wenn jede Folge aus
heißt (folgen-)kompakt, wenn jede Folge aus  eine konvergente Teilfolge mit Grenzwert in
eine konvergente Teilfolge mit Grenzwert in  besitzt.
besitzt.Jede kompakte Menge
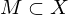 ist beschränkt und abgeschlossen bezüglich der Metrik
ist beschränkt und abgeschlossen bezüglich der Metrik 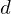 von
von 

