This flashcard is just one of a free flashcard set. See all flashcards!
1
Wie lauten die 4 klassischen Konstruierbarkeitsfragen der griechischen Antike?
1) Winkeldreiteilung:
Zu einem beliebigen gegebenen Winkel soll ein der Größe
soll ein der Größe 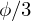 konstruiert werden.
konstruiert werden.
2) Delisches Problem:
Zu einem gegebenen Würfel der Kantenlänge a ist ein Würfel doppelten Volumens gesucht. Frage: Ist die neue Kantenlänge mit Zirkel und Lineal konstruierbar?
mit Zirkel und Lineal konstruierbar?
3) Quadratur des Kreises
Zu einem gegebenen Kreis soll ein Quadrat mit gleichem Flächeninhalt konstruiert werden. Frage: Ist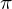 mit Zirkel und Lineal konstruierbar?
mit Zirkel und Lineal konstruierbar?
4) Konstruktion eines regelmässigen n-Ecks
Für welche n ist die Konstruktion eines regelmässigen n-Ecks möglich?
Zu einem beliebigen gegebenen Winkel
 soll ein der Größe
soll ein der Größe 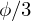 konstruiert werden.
konstruiert werden.2) Delisches Problem:
Zu einem gegebenen Würfel der Kantenlänge a ist ein Würfel doppelten Volumens gesucht. Frage: Ist die neue Kantenlänge
 mit Zirkel und Lineal konstruierbar?
mit Zirkel und Lineal konstruierbar?3) Quadratur des Kreises
Zu einem gegebenen Kreis soll ein Quadrat mit gleichem Flächeninhalt konstruiert werden. Frage: Ist
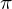 mit Zirkel und Lineal konstruierbar?
mit Zirkel und Lineal konstruierbar?4) Konstruktion eines regelmässigen n-Ecks
Für welche n ist die Konstruktion eines regelmässigen n-Ecks möglich?

