Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
40
Was ist ein Zufallsexperiment? Was ist eine Zufallsvariable? Was ist eine Wahrscheinlichkeit? Was ist eine Verteilungsfunktion? Was ist eine Dichtefunktion?
Mit Hilfe eines Zufallsexperiments werden zufällige Ergebnisse 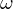 erzielt. Alle möglichen Ergebnisse ergeben die Ergebnismenge
erzielt. Alle möglichen Ergebnisse ergeben die Ergebnismenge  .
.
Eine Zufallsvariable ist eine Abbildung
ist eine Abbildung  , die ein Ergebnis auf eine reelle Zahl abbildet. Umgekehrt kann man sagen, dass die Zufallsvariablen "wahrscheinlichkeitsbehaftet" sind, also Zahlen mit gewissen Wahrscheinlichkeiten erzeugt werden.
, die ein Ergebnis auf eine reelle Zahl abbildet. Umgekehrt kann man sagen, dass die Zufallsvariablen "wahrscheinlichkeitsbehaftet" sind, also Zahlen mit gewissen Wahrscheinlichkeiten erzeugt werden.
Die Wahrscheinlichkeit , dass eine diskrete verteilte Zufallsvariable einen bestimmten Wert annimmt, erhält man z.B. durch Abzählen. Wahrscheinlichkeiten liegen im Wertebereich
, dass eine diskrete verteilte Zufallsvariable einen bestimmten Wert annimmt, erhält man z.B. durch Abzählen. Wahrscheinlichkeiten liegen im Wertebereich 
Interessiert man sich für die Wahrscheinlichkeit, dass in einem bestimmten Bereich liegt, benötigt man die Verteilungsfunktion:
in einem bestimmten Bereich liegt, benötigt man die Verteilungsfunktion:

Diese erhält man durch Aufsummieren der Wahrscheinlichkeiten. Die Verteilungsfunktion ist definiert im Bereich und nimmt Werte im Bereich
und nimmt Werte im Bereich  an.
an.
Bei einer stetig verteilten Zufallsvariablen ist die Wahrscheinlichkeit, dass ein bestimmtes Ergebnis annimmt Null. Die Wahrscheinlichkeiten können nur für Intervalle angegeben werden, d.h. man benötigt die Verteilungsfunktion.
ein bestimmtes Ergebnis annimmt Null. Die Wahrscheinlichkeiten können nur für Intervalle angegeben werden, d.h. man benötigt die Verteilungsfunktion.
Beispiel: Drehen eines Glücksrads.
Wie hoch ist die Wahrscheinlichkeit, dass das Rad von der Ausgangsposition einen Winkel von 42,2345° hat? 0
Wie hoch ist die Wahrscheinlichkeit, dass das Rad einen Winkel von 0 - 180° hat? 0,5
Bei stetig verteilten Zufallsvariablen gibt es keine Wahrscheinlichkeiten, sondern eine sogenannte Dichtefunktion. Die Verteilungsfunktion ergibt sich durch Integration.
Eine Zufallsvariable heißt stetig verteilt mit der Dichte
heißt stetig verteilt mit der Dichte  , falls sich ihre Verteilungsfunktion schreiben lässt als:
, falls sich ihre Verteilungsfunktion schreiben lässt als:

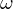 erzielt. Alle möglichen Ergebnisse ergeben die Ergebnismenge
erzielt. Alle möglichen Ergebnisse ergeben die Ergebnismenge  .
.Eine Zufallsvariable
 ist eine Abbildung
ist eine Abbildung  , die ein Ergebnis auf eine reelle Zahl abbildet. Umgekehrt kann man sagen, dass die Zufallsvariablen "wahrscheinlichkeitsbehaftet" sind, also Zahlen mit gewissen Wahrscheinlichkeiten erzeugt werden.
, die ein Ergebnis auf eine reelle Zahl abbildet. Umgekehrt kann man sagen, dass die Zufallsvariablen "wahrscheinlichkeitsbehaftet" sind, also Zahlen mit gewissen Wahrscheinlichkeiten erzeugt werden.Die Wahrscheinlichkeit
 , dass eine diskrete verteilte Zufallsvariable einen bestimmten Wert annimmt, erhält man z.B. durch Abzählen. Wahrscheinlichkeiten liegen im Wertebereich
, dass eine diskrete verteilte Zufallsvariable einen bestimmten Wert annimmt, erhält man z.B. durch Abzählen. Wahrscheinlichkeiten liegen im Wertebereich 
Interessiert man sich für die Wahrscheinlichkeit, dass
 in einem bestimmten Bereich liegt, benötigt man die Verteilungsfunktion:
in einem bestimmten Bereich liegt, benötigt man die Verteilungsfunktion: 
Diese erhält man durch Aufsummieren der Wahrscheinlichkeiten. Die Verteilungsfunktion ist definiert im Bereich
 und nimmt Werte im Bereich
und nimmt Werte im Bereich  an.
an.Bei einer stetig verteilten Zufallsvariablen ist die Wahrscheinlichkeit, dass
 ein bestimmtes Ergebnis annimmt Null. Die Wahrscheinlichkeiten können nur für Intervalle angegeben werden, d.h. man benötigt die Verteilungsfunktion.
ein bestimmtes Ergebnis annimmt Null. Die Wahrscheinlichkeiten können nur für Intervalle angegeben werden, d.h. man benötigt die Verteilungsfunktion.Beispiel: Drehen eines Glücksrads.
Wie hoch ist die Wahrscheinlichkeit, dass das Rad von der Ausgangsposition einen Winkel von 42,2345° hat? 0
Wie hoch ist die Wahrscheinlichkeit, dass das Rad einen Winkel von 0 - 180° hat? 0,5
Bei stetig verteilten Zufallsvariablen gibt es keine Wahrscheinlichkeiten, sondern eine sogenannte Dichtefunktion. Die Verteilungsfunktion ergibt sich durch Integration.
Eine Zufallsvariable
 heißt stetig verteilt mit der Dichte
heißt stetig verteilt mit der Dichte  , falls sich ihre Verteilungsfunktion schreiben lässt als:
, falls sich ihre Verteilungsfunktion schreiben lässt als:
Karteninfo:
Autor: Alex
Oberthema: Computergraphik
Schule / Uni: Universität Koblenz-Landau
Ort: Koblenz
Veröffentlicht: 05.07.2012

