Wie lautet die Rendering Equation? Was bedeutet sie?

- Das Licht
 , das von einem beliebigen Oberflächenelemente
, das von einem beliebigen Oberflächenelemente  in eine beliebige Richtung
in eine beliebige Richtung 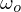 ausgestrahlt wird, ergibt sich aus:
ausgestrahlt wird, ergibt sich aus: - dem "Licht"
 , das von dem Oberflächenelement
, das von dem Oberflächenelement  in Richtung
in Richtung 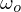 emittiert wird, plus
emittiert wird, plus - dem "Licht"
 , das von allen möglichen Einfallsrichtungen
, das von allen möglichen Einfallsrichtungen  einfällt und in Richtung
einfällt und in Richtung 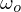 reflektiert wird.
reflektiert wird. -
 ist dabei die 6-dimensionale BRDF
ist dabei die 6-dimensionale BRDF
Was ist die BRDF?
Bi-Direktionale Reflexions-Verteilungsfunktion (Bi-directional Reflectance Distribution Function)
Analog für hinteren Halbraum: BTDF (Bi-directional Transmission Distribution Function) (Lichtbrechung!)

... gibt das Verhältnis der ausgehenden Leuchtdichte in eine bestimmte Richtung zur eingehenden Beleuchtungsstärke aus einer bestimmten Richtung an.
Einheit:
Liegt im Bereich
Analog für hinteren Halbraum: BTDF (Bi-directional Transmission Distribution Function) (Lichtbrechung!)

... gibt das Verhältnis der ausgehenden Leuchtdichte in eine bestimmte Richtung zur eingehenden Beleuchtungsstärke aus einer bestimmten Richtung an.
Einheit:

Liegt im Bereich

Eigenschaften einer BRDF?
Isotrope Materialien:
Anisotrope Materialien:
TODO: Verständliche Ergänzungen
- BRDF ist rotationssymetrisch und hängt nur von
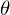 ab
ab - BRDF kann in einer beliebigen Ebene angegeben werden
- BRDF ist definiert durch einen Einfallswinkel und zwei Ausfallswinkel
Anisotrope Materialien:
- BRDF ist allgemein abhängig von zwei Einfallswinkeln und zwei Ausfallswinkeln
- Koordinatensystem muss durch weitere Achse festgelegt werden
TODO: Verständliche Ergänzungen
Wann ist eine BRDF physikalisch plausibel?
1. Sie ist nicht negativ
2. Sie erfüllt den Energieerhaltungssatz
3. Sie erfüllt die Helmholtz Reziprozität
2. Sie erfüllt den Energieerhaltungssatz
-

- Es darf nicht mehr Licht rausgehen als reinkommt! (Licht wird reflektiert und nicht erzeugt)
3. Sie erfüllt die Helmholtz Reziprozität
- Lichtstrom ist vorwärts wie rückwärts identisch
-

Was ist der Reflexionsgrad 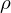 ?
?
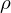 ?
?Der Reflexionsgrad ist definiert als der gesamte ausfallende Lichtstrom im Verhältnis zum gesamten eingestrahlten Lichtstrom.

Liegt im Bereich (vgl. Energieerhaltungssatz)
(vgl. Energieerhaltungssatz)
Nicht für zwei Richtungen definiert (wie BRDF), sondern über gesamte Hemisphäre und kann so gesehen als Integration über die BRDF gesehen werden.

Liegt im Bereich
 (vgl. Energieerhaltungssatz)
(vgl. Energieerhaltungssatz)Nicht für zwei Richtungen definiert (wie BRDF), sondern über gesamte Hemisphäre und kann so gesehen als Integration über die BRDF gesehen werden.
Wie lautet die BRDF für den diffusen Fall?
Diffuse Reflexion bedeutet, dass das Licht in alle Richtungen gleich gestreut wird, unabhängig von der Einfallsrichtung, d.h. die BRDF ist konstant.



Die reflektierte Leuchtdichte ist proportional zur einfallenden Beleuchtungsstärke.
Reflektierte Leuchtdichte ist konstant und die gleiche in allen Richtungen - unabhängig von der Einfallsrichtung.
Für die diffuse Lambert-Reflexion gilt für den Reflexionsgrad:



Daraus folgt: bzw.
bzw. 



Die reflektierte Leuchtdichte ist proportional zur einfallenden Beleuchtungsstärke.
Reflektierte Leuchtdichte ist konstant und die gleiche in allen Richtungen - unabhängig von der Einfallsrichtung.
Für die diffuse Lambert-Reflexion gilt für den Reflexionsgrad:



Daraus folgt:
 bzw.
bzw. 
Was ist ein Formfaktor?
Ein Formfaktor bezeichnet den Anteil der versendeten Strahlung, die beim Empfänger an kommt.

Der Lichtstrom, der von einem Sender s bei einem Empfänger e ankommt, berechnet sich aus dem Lichtstrom des Senders mal dem Formfaktor , mit
, mit

Bei dem Formfaktor handelt es sich eigentlich um ein 4-fach Integral (je zwei Parameter pro Fläche).

Der Lichtstrom, der von einem Sender s bei einem Empfänger e ankommt, berechnet sich aus dem Lichtstrom des Senders mal dem Formfaktor
 , mit
, mit
Bei dem Formfaktor handelt es sich eigentlich um ein 4-fach Integral (je zwei Parameter pro Fläche).
Was ist die 1. Formfaktorvereinfachung?
Annahme: Senderfläche sehr klein.
Integration über Empfängerfläche liefert praktisch konstanten Wert für jedes und kann damit vor das Integral gezogen werden.
und kann damit vor das Integral gezogen werden.
"Formfaktor zwischen einer infinitesimalen Senderfläche und einer finiten Empfängerfläche."

Integration über Empfängerfläche liefert praktisch konstanten Wert für jedes
 und kann damit vor das Integral gezogen werden.
und kann damit vor das Integral gezogen werden."Formfaktor zwischen einer infinitesimalen Senderfläche und einer finiten Empfängerfläche."

Was ist die 2. Formfaktorvereinfachung?
Annahme: Sender- und Empfängerfläche sehr klein.
Flächenunabhängige Teil des Integrals bleibt konstant über die Integration von und kann somit vor das Integral gezogen werden.
und kann somit vor das Integral gezogen werden.
"Formfaktor zwischen einer infinitesimalen Senderfläche und einer infinitesimalen Empfängerfläche."

Flächenunabhängige Teil des Integrals bleibt konstant über die Integration von
 und kann somit vor das Integral gezogen werden.
und kann somit vor das Integral gezogen werden."Formfaktor zwischen einer infinitesimalen Senderfläche und einer infinitesimalen Empfängerfläche."

Wie kann die Visibilität bestimmt werden?
Visibilität kann durch Ray Tracing bestimmt werden.
Zwei Möglichkeiten:
1. Möglichkeit:
Für jedes Pixel einen Prisma-FF berechnen, falls sichtbar und aufaddieren.
2. Möglichkeit:
Visibilitätsfaktor V berechnen. V ist die Anzahl der Treffer (1) im Verhältnis zu allen versendeten Strahlen (V liegt dann im Bereich ).
).
Danach Prisma-FF für gesamte Situation berechnen und mit V multiplizieren.
- NxN Raster über die flächige Lichtquelle
- Schicke Strahl (Schattenfühler) von
 zu jedem Mittelpunkt der Rasterfläche (jittering)
zu jedem Mittelpunkt der Rasterfläche (jittering) - Jeder Strahl liefert dann "sichtbar" (1) oder "unsichtbar" (0)
Zwei Möglichkeiten:
1. Möglichkeit:
Für jedes Pixel einen Prisma-FF berechnen, falls sichtbar und aufaddieren.
2. Möglichkeit:
Visibilitätsfaktor V berechnen. V ist die Anzahl der Treffer (1) im Verhältnis zu allen versendeten Strahlen (V liegt dann im Bereich
 ).
).Danach Prisma-FF für gesamte Situation berechnen und mit V multiplizieren.
Wie kann die Rendering Equation gelöst werden?
Eine analytische Lösung der Rendering Equation ist nicht denkbar, da es sich eigentlich um ein Doppelintegral handelt und die BRDF mindestens 6-dimensional ist. Daher versuchen alle Verfahren, die Rendering Equation zu vereinfachen und/oder zu approximieren. Die Ansätze können dabei in Radiosity-Verfahren und Ray-Tracing-Verfahren unterteilt werden.
Welche Grundannahmen werden beim Radiosity-Ansatz gemaht?
1. Die Umgebung wird als vollständig diffus angenommen.
2. Szene wird so in Patches aufgeteilt, dass die Radiosity pro Patch als konstant angenommen werden kann.
Aus den beiden Annahmen ergibt sich die folgende Radiosity-Gleichung:

2. Szene wird so in Patches aufgeteilt, dass die Radiosity pro Patch als konstant angenommen werden kann.
Aus den beiden Annahmen ergibt sich die folgende Radiosity-Gleichung:

Wie lässt sich die Radiosity-Gleichung aus der Rendering Equation herleiten (grob)?

Die BRDF für den diffusen Fall ist konstant und kann vor das Integral gezogen werden. Weiterhin ist die reflektierte Leuchtdichte konstant und die gleiche in alle Richtungen:

Zusätzlich gilt für den diffusen Fall:
 und damit
und damit  bzw.
bzw.  . Die Multiplikation der vorherigen Gleichung mit
. Die Multiplikation der vorherigen Gleichung mit 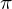 liefert somit:
liefert somit:
Unter der Annahme, dass die Szene so in Patches unterteilt wird, dass die Radiosity pro Patch als konstant angenommen werden kann, lässt sich das Integral durch eine Summe ersetzen:

(Der letzte Schritt ist nur eine grobe Herleitung. Hier fehlen noch einige Zwischenschritte.)
Wie funktioniert Progressive Refinement?
Für jedes Patch werden zwei Radiositywerte abgespeichert:
Initialisierung beider Werte durch Eigenemission:
Suche zu Beginn einer Relaxation das Patch mit der größten noch nicht versendeten Radiosity (Senderpatch).
Berechne N Formfaktoren.
Radiosityaustausch vom Sender zu allen Empfängern:
Unversendete Radiosity des Senders auf 0 setzen.
- Absolute Radiosity

- Unversendete (Unshot) Radiosity

Initialisierung beider Werte durch Eigenemission:
Suche zu Beginn einer Relaxation das Patch mit der größten noch nicht versendeten Radiosity (Senderpatch).
Berechne N Formfaktoren.
Radiosityaustausch vom Sender zu allen Empfängern:
Unversendete Radiosity des Senders auf 0 setzen.
Gibt es eine bessere Möglichkeit das Senderpatch auszuwählen? Wenn ja, warum?
Eine bessere Möglichkeit als die Unversendete Radiosity wäre der Unversendete Lichtstrom, da hier die Fläche  mitbetrachtet wird. Es wäre beispielsweise denkbar, dass eine Fläche zwar einen hohen Wert an unversendeter Radiosity hat, die Fläche aber so klein ist, dass sie nur einen kleinen Beitrag leistet.
mitbetrachtet wird. Es wäre beispielsweise denkbar, dass eine Fläche zwar einen hohen Wert an unversendeter Radiosity hat, die Fläche aber so klein ist, dass sie nur einen kleinen Beitrag leistet.
 mitbetrachtet wird. Es wäre beispielsweise denkbar, dass eine Fläche zwar einen hohen Wert an unversendeter Radiosity hat, die Fläche aber so klein ist, dass sie nur einen kleinen Beitrag leistet.
mitbetrachtet wird. Es wäre beispielsweise denkbar, dass eine Fläche zwar einen hohen Wert an unversendeter Radiosity hat, die Fläche aber so klein ist, dass sie nur einen kleinen Beitrag leistet.Wo liegt das Problem bei der Auswahl des Senderpatches beim Progressive Refinement?
Das Problem liegt darin, dass der Radiositywert ein rgb-Vektor ist, mit dem man keine genaue Aussage über die Helligkeit eines Patches machen kann. Es wäre möglich die rgb-Werte aufzusummieren und nach das Patch mit der größten Summe als Senderpatch auszuwählen.
Besser ist jedoch die Farbmatrix für das aktuelle Display zu bestimmen und mit deren Hilfe den rgb-Wert in einen XYZ-Wert umzurechnen. Der Radiositywert steckt dann in der Y-Komponente. Für jedes Patch muss dann die folgende Gleichung ausgewertet werden zur Suche nach dem maximalen unshot Lichtstrom:

 bezeichnet hierbei das photometrische Strahlungsäquivalent. Dieser Wert ist konstant und kann daher zur Suche nach dem hellsten Patch weggelassen werden.
bezeichnet hierbei das photometrische Strahlungsäquivalent. Dieser Wert ist konstant und kann daher zur Suche nach dem hellsten Patch weggelassen werden.
Besser ist jedoch die Farbmatrix für das aktuelle Display zu bestimmen und mit deren Hilfe den rgb-Wert in einen XYZ-Wert umzurechnen. Der Radiositywert steckt dann in der Y-Komponente. Für jedes Patch muss dann die folgende Gleichung ausgewertet werden zur Suche nach dem maximalen unshot Lichtstrom:

 bezeichnet hierbei das photometrische Strahlungsäquivalent. Dieser Wert ist konstant und kann daher zur Suche nach dem hellsten Patch weggelassen werden.
bezeichnet hierbei das photometrische Strahlungsäquivalent. Dieser Wert ist konstant und kann daher zur Suche nach dem hellsten Patch weggelassen werden.Was wird noch zur Darstellung beim Progressive Refinement benötigt?
Ambienter Term:
Nur für die Darstellung!
Verfahren:
Abschätzung eines mittleren Formfaktors:

Abschätzung eines mittleren Reflexiongrades:





Tone-Mapping:
Abbildung der rgb-Werte von auf den darstellbaren Bereich von
auf den darstellbaren Bereich von 
Extrapolation der Eckpunkte.
Nur für die Darstellung!
Verfahren:
Abschätzung eines mittleren Formfaktors:

Abschätzung eines mittleren Reflexiongrades:





Tone-Mapping:
Abbildung der rgb-Werte von
 auf den darstellbaren Bereich von
auf den darstellbaren Bereich von 
Extrapolation der Eckpunkte.
Welche Nachteile/Artefakte entstehen bei einer regulären Aufteilung der Szene in Patches?
Nachteile:
Artefakte:
- Zu viele Patches dort, wo sie nicht gebraucht werden.
- Zu wenig Patches dort, wo sie gebraucht werden.
- Artefakte
Artefakte:
- Fehlende Schatten, schwebende Objekte
- Gezackte Schattengrenzen
- Schatten- und Lichtlöcher
- Nähte
- Mach-Bänder
Wie funktioniert die adaptive Unterteilung von Patches?
Gegeben sind zwei Flächen, der Formfaktor zwischen den beiden Flächen, die Sichtbarkeit und die Radiosity, die ausgetauscht werden soll.
Es muss nun eine Funktion geben, die auf Basis dieser Informationen entscheidet, ob eine Unterteilung notwendig ist oder nicht. Eine solche Funktion wird als Orakel bezeichnet. Wichtige Orakel sind:
Verwendete Datenstruktur: Quadtree!
Es muss nun eine Funktion geben, die auf Basis dieser Informationen entscheidet, ob eine Unterteilung notwendig ist oder nicht. Eine solche Funktion wird als Orakel bezeichnet. Wichtige Orakel sind:
- Sichtbarkeitsorakel
- BFA-Kriterium
- Lischinksi-Kriterium
- Gradientenbasiertes Unterteilung
Verwendete Datenstruktur: Quadtree!
Wie funktioniert das BFA-Orakel mit Visibilität?
Signatur der Orkal-Funktion: bool oracle(s, e, vis, ff)
1. Testen, ob überhaupt genügend Lichtstrom unterwegs ist, sodass sich eine weitere Überprüfung überhaupt lohnt:

2. Überprüfung der Sichtbarkeit:
Bewertung: Es hängt sehr stark von der initialen Patchaufteilung ab, ob lokale Maxima verpasst werden.
1. Testen, ob überhaupt genügend Lichtstrom unterwegs ist, sodass sich eine weitere Überprüfung überhaupt lohnt:

2. Überprüfung der Sichtbarkeit:
- Falls totale Verdeckung: Keine Unterteilung.
- Falls partielle Verdeckung: Immer unterteilen.
- Falls SPS: Immer unterteilen.
- Falls unverdeckt: Prüfen, ob der versendete Lichtstrom groß genug ist, sodass eine Unterteilung sinnvoll ist:

Bewertung: Es hängt sehr stark von der initialen Patchaufteilung ab, ob lokale Maxima verpasst werden.
Was ist die Idee hinter dem Lischinski-Kriterium?
Idee: Unterteilung, wenn der aktuelle Wert der konstanten Funktion zu stark abweicht von der tatsächlichen Radiosity-Funktion.
Bestimmung bzw. Abschätzung der lokalen Minima und Maxima der Radiosity-Funktion innerhalb eines Patches.
Beobachtung: Radiosity-Funktion ist monoton und stetig im vollständig sichtbaren Bereich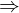
Bestimmung bzw. Abschätzung der lokalen Minima und Maxima der Radiosity-Funktion innerhalb eines Patches.
Beobachtung: Radiosity-Funktion ist monoton und stetig im vollständig sichtbaren Bereich
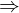
- Maximum ist entweder innerhalb der Patchgrenzen oder auf den Kanten
- Minimum liegt auf den Patch Kanten
Wie entscheidet man nun konkret mit dem Lischinski-Kriterium, ob unterteilt wird oder nicht?
Berechnung von 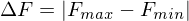 .
.
Unterteilung, wenn

Total Verdeckung:
Partielle Verdeckung:
Keine Verdeckung:
Berechnung des Minimums und Maximums: Berechnung von 5 Formfaktoren (4 Eckpunkte und Mittelpunkt) und daraus das Minimum und Maximum bestimmen.
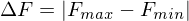 .
.Unterteilung, wenn

Total Verdeckung:
Partielle Verdeckung:
-

-
 für unverdeckten Fall berechnen.
für unverdeckten Fall berechnen.
Keine Verdeckung:
-
 liegt auf den Kanten des Patches
liegt auf den Kanten des Patches -
 liegt auf den Kanten oder innerhalb des Patches
liegt auf den Kanten oder innerhalb des Patches
Berechnung des Minimums und Maximums: Berechnung von 5 Formfaktoren (4 Eckpunkte und Mittelpunkt) und daraus das Minimum und Maximum bestimmen.
Wie funktioniert hierarchisches Radiosity?
Allgemeiner Ablauf:
Initial Linking
Repeat
Refine
Gather
PushPull
Until Converged
(1) Initial Linking:
(2) Refine
(3) Gather
(4) PushPull
Initial Linking
Repeat
Refine
Gather
PushPull
Until Converged
(1) Initial Linking:
- Verlinkt alle Root-Knoten miteinander in beide Richtung (Gahter-Links)
-

- Liste mit Links
(2) Refine
- Alle Links werden untersucht (Schleife über alle Links)
- Wird ein Link refined, wird der Vaterlink gelöscht und 4 neue Links bei den Kindern von e eingetragen (falls Empfänger refined wird)oderDer Empfänger mit den 4 Kindern des Senders verlinkt (falls Sender refined wird)
- Wann wird unterteilt? BFA, Lischinski
- Welche Fläche wird unterteilt (Sender oder Empfänger)? z.B. größere Fläche, größerer FF
(3) Gather
- Schleife über alle Links
- Radiosity wird für jeden Link beim Empfänger eingesammelt:

(4) PushPull
- Hierarchie konsistent machen
- Radiosity-Werte in Blättern müssen konsistent sein für die Darstellung
- Radiosity-Werte in Knoten müssen konsistent sein für den Radiosity-Austausch
- Push: Radiosity Wert auf Kinder aufaddieren.
- Pull: Flächengewichteten Mittelwert der Kinderradiosities bilden.


Was ist der genaue Vorteil von hierarchischem Radiosity gegenüber Progressive Refinement?
Der Nachteil beim Progressive Refinement ist, dass von einem Sender aus alle kleinen Patches der Welt betrachtet werden müssen.
Beispiel: Der Sender ist das Patch einer kleinen Steckdose. Dieses Patch soll Radiosity mit einer großen Wand austauschen. Beim Progressive Refinement muss nun alle an kleinen Patches der Wand, die aufgrund des vorherigen Radiosity-Austauschs enstanden sind, Radiosity verschießen, obwohl die Steckdose nur einen sehr kleinen Beitrag leistet. Der Vorteil beim hierarchischen Radiosity liegt darin, dass die Steckdose nun auf einen viel höheren Level Radiosity mit der Wand austauschen kann, z.B. mit der kompletten Wand oder großen Teilen davon.
Beispiel: Der Sender ist das Patch einer kleinen Steckdose. Dieses Patch soll Radiosity mit einer großen Wand austauschen. Beim Progressive Refinement muss nun alle an kleinen Patches der Wand, die aufgrund des vorherigen Radiosity-Austauschs enstanden sind, Radiosity verschießen, obwohl die Steckdose nur einen sehr kleinen Beitrag leistet. Der Vorteil beim hierarchischen Radiosity liegt darin, dass die Steckdose nun auf einen viel höheren Level Radiosity mit der Wand austauschen kann, z.B. mit der kompletten Wand oder großen Teilen davon.
Wozu benötigt man Tone-Mapping?
Tone-Mapping wird benötigt, wenn die rgb-Werte außerhalb des durch das Display darstellbaren Bereichs liegen.
Auf der x-Achse wird die Leuchtdichte der realen Welt aufgetragen und auf der y-Achse die Leuchtdichte des Displays.
Lineares Mapping:
Logarithmisches Mapping (URQV):

Auf der x-Achse wird die Leuchtdichte der realen Welt aufgetragen und auf der y-Achse die Leuchtdichte des Displays.
Lineares Mapping:
- Maximaler Radiosity-Wert (außer Lichtquellen) wird auf 1 abgebildet
Logarithmisches Mapping (URQV):

Was ist ein Zufallsexperiment? Was ist eine Zufallsvariable? Was ist eine Wahrscheinlichkeit? Was ist eine Verteilungsfunktion? Was ist eine Dichtefunktion?
Mit Hilfe eines Zufallsexperiments werden zufällige Ergebnisse 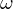 erzielt. Alle möglichen Ergebnisse ergeben die Ergebnismenge
erzielt. Alle möglichen Ergebnisse ergeben die Ergebnismenge  .
.
Eine Zufallsvariable ist eine Abbildung
ist eine Abbildung  , die ein Ergebnis auf eine reelle Zahl abbildet. Umgekehrt kann man sagen, dass die Zufallsvariablen "wahrscheinlichkeitsbehaftet" sind, also Zahlen mit gewissen Wahrscheinlichkeiten erzeugt werden.
, die ein Ergebnis auf eine reelle Zahl abbildet. Umgekehrt kann man sagen, dass die Zufallsvariablen "wahrscheinlichkeitsbehaftet" sind, also Zahlen mit gewissen Wahrscheinlichkeiten erzeugt werden.
Die Wahrscheinlichkeit , dass eine diskrete verteilte Zufallsvariable einen bestimmten Wert annimmt, erhält man z.B. durch Abzählen. Wahrscheinlichkeiten liegen im Wertebereich
, dass eine diskrete verteilte Zufallsvariable einen bestimmten Wert annimmt, erhält man z.B. durch Abzählen. Wahrscheinlichkeiten liegen im Wertebereich 
Interessiert man sich für die Wahrscheinlichkeit, dass in einem bestimmten Bereich liegt, benötigt man die Verteilungsfunktion:
in einem bestimmten Bereich liegt, benötigt man die Verteilungsfunktion:

Diese erhält man durch Aufsummieren der Wahrscheinlichkeiten. Die Verteilungsfunktion ist definiert im Bereich und nimmt Werte im Bereich
und nimmt Werte im Bereich  an.
an.
Bei einer stetig verteilten Zufallsvariablen ist die Wahrscheinlichkeit, dass ein bestimmtes Ergebnis annimmt Null. Die Wahrscheinlichkeiten können nur für Intervalle angegeben werden, d.h. man benötigt die Verteilungsfunktion.
ein bestimmtes Ergebnis annimmt Null. Die Wahrscheinlichkeiten können nur für Intervalle angegeben werden, d.h. man benötigt die Verteilungsfunktion.
Beispiel: Drehen eines Glücksrads.
Wie hoch ist die Wahrscheinlichkeit, dass das Rad von der Ausgangsposition einen Winkel von 42,2345° hat? 0
Wie hoch ist die Wahrscheinlichkeit, dass das Rad einen Winkel von 0 - 180° hat? 0,5
Bei stetig verteilten Zufallsvariablen gibt es keine Wahrscheinlichkeiten, sondern eine sogenannte Dichtefunktion. Die Verteilungsfunktion ergibt sich durch Integration.
Eine Zufallsvariable heißt stetig verteilt mit der Dichte
heißt stetig verteilt mit der Dichte  , falls sich ihre Verteilungsfunktion schreiben lässt als:
, falls sich ihre Verteilungsfunktion schreiben lässt als:

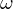 erzielt. Alle möglichen Ergebnisse ergeben die Ergebnismenge
erzielt. Alle möglichen Ergebnisse ergeben die Ergebnismenge  .
.Eine Zufallsvariable
 ist eine Abbildung
ist eine Abbildung  , die ein Ergebnis auf eine reelle Zahl abbildet. Umgekehrt kann man sagen, dass die Zufallsvariablen "wahrscheinlichkeitsbehaftet" sind, also Zahlen mit gewissen Wahrscheinlichkeiten erzeugt werden.
, die ein Ergebnis auf eine reelle Zahl abbildet. Umgekehrt kann man sagen, dass die Zufallsvariablen "wahrscheinlichkeitsbehaftet" sind, also Zahlen mit gewissen Wahrscheinlichkeiten erzeugt werden.Die Wahrscheinlichkeit
 , dass eine diskrete verteilte Zufallsvariable einen bestimmten Wert annimmt, erhält man z.B. durch Abzählen. Wahrscheinlichkeiten liegen im Wertebereich
, dass eine diskrete verteilte Zufallsvariable einen bestimmten Wert annimmt, erhält man z.B. durch Abzählen. Wahrscheinlichkeiten liegen im Wertebereich 
Interessiert man sich für die Wahrscheinlichkeit, dass
 in einem bestimmten Bereich liegt, benötigt man die Verteilungsfunktion:
in einem bestimmten Bereich liegt, benötigt man die Verteilungsfunktion: 
Diese erhält man durch Aufsummieren der Wahrscheinlichkeiten. Die Verteilungsfunktion ist definiert im Bereich
 und nimmt Werte im Bereich
und nimmt Werte im Bereich  an.
an.Bei einer stetig verteilten Zufallsvariablen ist die Wahrscheinlichkeit, dass
 ein bestimmtes Ergebnis annimmt Null. Die Wahrscheinlichkeiten können nur für Intervalle angegeben werden, d.h. man benötigt die Verteilungsfunktion.
ein bestimmtes Ergebnis annimmt Null. Die Wahrscheinlichkeiten können nur für Intervalle angegeben werden, d.h. man benötigt die Verteilungsfunktion.Beispiel: Drehen eines Glücksrads.
Wie hoch ist die Wahrscheinlichkeit, dass das Rad von der Ausgangsposition einen Winkel von 42,2345° hat? 0
Wie hoch ist die Wahrscheinlichkeit, dass das Rad einen Winkel von 0 - 180° hat? 0,5
Bei stetig verteilten Zufallsvariablen gibt es keine Wahrscheinlichkeiten, sondern eine sogenannte Dichtefunktion. Die Verteilungsfunktion ergibt sich durch Integration.
Eine Zufallsvariable
 heißt stetig verteilt mit der Dichte
heißt stetig verteilt mit der Dichte  , falls sich ihre Verteilungsfunktion schreiben lässt als:
, falls sich ihre Verteilungsfunktion schreiben lässt als:
Welche Eigenschaften muss eine Dichte haben? Welche Eigenschaften haben Verteilungsfunktionen einer stetig verteilten Zufallsvariable?
Eigenschaften einer Dichte:
Eigenschaften einer Verteilungsfunktion:
- Werte immer positiv (>0)
- Fläche unter der Kurve muss Eins sein:

Eigenschaften einer Verteilungsfunktion:
- Monoton steigend
- Werte im Bereich

Ist die BRDF eine Dichtefunktion?
Nein, denn eine Eigenschaft einer physikalisch plausiblen BRDF ist der Energieerhaltungssatz, der besagt:

Der Reflexionsgrad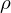 ist die Integration über die BRDF.
ist die Integration über die BRDF.
Wie zuvor gesehen, ist jedoch eine Eigenschafte einer Dichte, dass die Fläche unter der Kurve Eins sein muss.

Der Reflexionsgrad
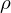 ist die Integration über die BRDF.
ist die Integration über die BRDF.Wie zuvor gesehen, ist jedoch eine Eigenschafte einer Dichte, dass die Fläche unter der Kurve Eins sein muss.
Wie erzeugt man Zufallszahlen mit einer bestimmten Dichte?
Zufallszahlen mit einer bestimmten Dichte lassen sich mit Hilfe der inversen CDF-Methoden erzeugen (CDF = cumulative distribution function).
Vorgehen:
Vorgehen:
- Bestimme die Verteilungsfunktion F
- Invertiere diese
- Ergebnis: Zufallsvariable mit der gewünschten Dichte aus einer (0,1)-Verteilung
Wie lässt sich der Formfaktor (1. Vereinfachung) mit Hilfe der Monte-Carlo-Integration berechnen?

Wählt man als gleichverteilte Dichte

so erhält man durch Einsetzen in die Monte-Carlo Gleichung:

Der Teil nach dem Summenzeichen entspricht der 2. Formfaktorvereinfachung. Mit Hilfe dieser Formel könnte man beispielsweise die Beleuchtung mit einer flächigen Lichtquelle an einem bestimmten Punkt berechnen. Hierzu wählt man N zufällige Punkte auf der Lichtquelle aus, berechnet jeweils den Formfaktor (2. Vereinfachung), summiert diesen auf und teilt durch die Anzahl N der Samples.
Wichtig: Bei der 2. Formfaktorvereinfachung kann der Formfaktor > 1 werden. Daher muss das Ergebnis am Ende geclippt werden. Man darf nicht vorher clippen, da sonst ein Fehler eingebaut wird und das Ergebnis verfälscht wird.
Wie funktioniert Path Tracing?
Grundidee:
- Durch jedes Pixel werden n Strahlen versendet (jittering, stratified sampling)
- Trifft der Sehstrahl auf eine Oberfläche, werden nicht n Strahlen weiterverfolgt, sondern immer nur einer
- Für jeden Strahl wird an jeder Oberfläche jeweils ein Pfad (Path) ausgesucht und weiterverfolgt
Wo verwendet man beim Path Tracing Stratified Sampling?
Stratified Sampling wird bei der Bestimmung des direkten Lichts verwendet, da dieses für jeden Schnittpunkt extra abgetastet wird, d.h. man zerlegt die Halbkugel in Bereiche des direkten und des indirekten Lichts.
Wichtig: Der zufällig erzeugte Strahl, der das indirekte Licht einsammeln soll, darf nicht in Richtung des direkten Lichts versendet werden, da dieses sonst doppelt abgetastet wird.
Wichtig: Der zufällig erzeugte Strahl, der das indirekte Licht einsammeln soll, darf nicht in Richtung des direkten Lichts versendet werden, da dieses sonst doppelt abgetastet wird.
Was ist "Russisches Roulette"?
Russisches Roulette wird verwendet, um zu entscheiden, welcher Path weiterverfolgt wird.
Beispiel:
Ein Material besteht aus einer diffusen Komponente , einer spiegelnden Komponente
, einer spiegelnden Komponente  und einer transmittierenden Komponenten
und einer transmittierenden Komponenten 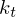 , wobei gilt
, wobei gilt  .
.
Um zu entscheiden, ob der diffuse, spiegelnde oder transmittierende Strahl weiterverfolgt wird, wird eine Zufallszahl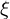 erzeugt:
erzeugt:
 diffus
diffus
 reflexion
reflexion
 transmission
transmission
Beispiel:
Ein Material besteht aus einer diffusen Komponente
 , einer spiegelnden Komponente
, einer spiegelnden Komponente  und einer transmittierenden Komponenten
und einer transmittierenden Komponenten 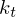 , wobei gilt
, wobei gilt  .
. Um zu entscheiden, ob der diffuse, spiegelnde oder transmittierende Strahl weiterverfolgt wird, wird eine Zufallszahl
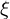 erzeugt:
erzeugt: diffus
diffus reflexion
reflexion transmission
transmissionErläutern Sie die erste Stufe des Photon Mappings genauer!
1. Photon Emission
2. Photon Tracing/Scattering
3. Photon Storing
- Lichtquellen müssen Photonen emittieren
- Wenn eine Lichtquelle N Photonen versendet, dann trägt jedes Photon genau den 1/N-ten Teil des Lichtstroms
- In welche Richtung werden Photonen emittiert?
 LVK als Dichtefunktion
LVK als Dichtefunktion
2. Photon Tracing/Scattering
- Trifft ein Photon auf eine Oberfläche wird mit Hilfe von russischem Roulette entschieden, wie es weitergeht
- Nur ein Weg wird weiterverfolgt
- Diffuse Fläche: Photon wird mit der aktuellen Position in der Photon Map gespeichert und eine neue Richtung durch Importance Sampling erzeugt.
- Reflexion/Transmission: Photon wird in der entsprechenden Richtung weiterverfolgt und nicht abgespeichert
- Absorption: Photon wird gespeichert und nicht weiterverfolgt
3. Photon Storing
- float position[3] unsigned char theta, phifloat power[3]short plane
- Organisation mittels kd-Tree
Was ist ein kd-Tree? Warum verwendet man ihn beim Photon Mapping?
Ein kd-Tree ist ein binärer Suchbaum in 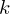 Dimensionen.
Dimensionen.
Man verwendet beim Photon Mapping einen binären Suchbaum, weil dieser speichereffizient ist und die Nearest Neighbor Suche, die für den Radiance Estimate benötigt wird sehr effizient ist.
Erzeugung:
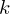 Dimensionen.
Dimensionen.Man verwendet beim Photon Mapping einen binären Suchbaum, weil dieser speichereffizient ist und die Nearest Neighbor Suche, die für den Radiance Estimate benötigt wird sehr effizient ist.
Erzeugung:
- Suche die Raumachse mit der größten Ausdehnung
- Entlang dieser Achse werden alle Photonen sortiert
- Das mittlere Photon wird ein neuer Knoten im Baum
- Alle kleineren Photonen kommen in den linken Teilbaum, alle größeren in den rechten
- Rekursive Anwendung auf beide Teilbäme
Wie kann man mit Hilfe des Photon Mappings und des Radiance Estimates ein Bild rendern?
Es gibt viele Möglichkeiten ein Bild zu rendern:
1. Direkte Auswertung der Photon Map
2. Path Tracing mit Photon Mapping
3. Final Gathering mit Photon Mapping
1. Direkte Auswertung der Photon Map
- Liefert verrauschte Bilder
2. Path Tracing mit Photon Mapping
- Viele Strahlen durch ein Pixel
- Für jeden Schnittpunkt - Direktes Licht berechnen (1 Sample) - Caustic Map auswerten - Per russischem Roulette diffus oder spiegelnd weiterverfolg.
- Beim indirekten Licht Photon Maps auswerten bzw. Spiegel weiterverfolgen
3. Final Gathering mit Photon Mapping
- Wenige Strahlen durch ein Pixel
- Für jeden Schnittpunkt: - Direktes Licht berechnen (viele Samples) - Caustic Map auswerten - Halbraum durch viele Strahlen abtasten, wobei die Photon Maps ausgewertet werden - Spiegelung rekursiv weiterverfolgen - Alle Anteile gemäß BRDF gewichten
Flashcard set info:
Author: Alex
Main topic: Computergraphik
School / Univ.: Universität Koblenz-Landau
City: Koblenz
Published: 05.07.2012
Card tags:
All cards (58)
no tags








 (lx)
(lx)

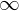






 die normierte Normale der Senderfläche ist und
die normierte Normale der Senderfläche ist und  ein Vektor, dessen Betrag durch den Winkel einer Pyramidenseite gegeben ist und dessen Richtung senkrecht auf der Pyramidenseite steht.
ein Vektor, dessen Betrag durch den Winkel einer Pyramidenseite gegeben ist und dessen Richtung senkrecht auf der Pyramidenseite steht.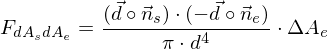
 und nicht
und nicht  ?
?






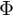 (und A), sowie eine rgb-Farbe. Wie berechnet man die Radiosity?
(und A), sowie eine rgb-Farbe. Wie berechnet man die Radiosity?





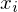 Zufallszahlen sind, die mit der Dichte
Zufallszahlen sind, die mit der Dichte  erhält man die Formel der Monte-Carlo-Integration:
erhält man die Formel der Monte-Carlo-Integration:
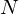 zum Erwartungswert konvergiert.
zum Erwartungswert konvergiert.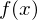 möglichst ähnlich ist:
möglichst ähnlich ist:


