Theorem 0.1 Division Algorithm
Let  and
and 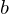 be integers with
be integers with 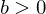 . Then
. Then 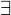 unique integers
unique integers 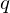 and
and 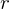 with the property that
with the property that 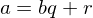 , where
, where  .
.
 and
and 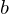 be integers with
be integers with 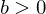 . Then
. Then 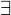 unique integers
unique integers 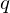 and
and 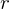 with the property that
with the property that 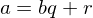 , where
, where  .
.Theorem 0.2 GCD is a Linear Combination
For any nonzero integers  and
and 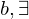 integers
integers  and
and 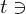 gcd(
gcd(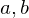 )
)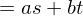 . Moreover, gcd(
. Moreover, gcd(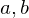 ) is the smallest positive integer of the form
) is the smallest positive integer of the form 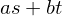 .
.
 and
and 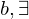 integers
integers  and
and 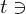 gcd(
gcd(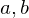 )
)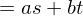 . Moreover, gcd(
. Moreover, gcd(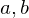 ) is the smallest positive integer of the form
) is the smallest positive integer of the form 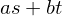 .
.Theorem 0.3 Fundamental Theorem of Arithmetic
Every integer greater than 1 is a prime or the unique product of primes.
Theorem 0.4 First Principle of Mathematical Induction
Let  be a set of integers containing
be a set of integers containing  . Suppose
. Suppose  has the property that whenever some integer
has the property that whenever some integer 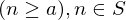 , then the integer
, then the integer 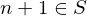 . Then,
. Then,  contains every integer greater than or equal to
contains every integer greater than or equal to  .
.
 be a set of integers containing
be a set of integers containing  . Suppose
. Suppose  has the property that whenever some integer
has the property that whenever some integer 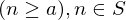 , then the integer
, then the integer 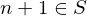 . Then,
. Then,  contains every integer greater than or equal to
contains every integer greater than or equal to  .
.Theorem 0.5 Second Principle of Mathematical Induction
Let  be a set of integers containing
be a set of integers containing  . Suppose
. Suppose  has the property that
has the property that 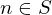 whenever every integer less than
whenever every integer less than 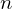 and greater than or equal to
and greater than or equal to  belongs to
belongs to  . Then,
. Then,  contains every integer greater than or equal to
contains every integer greater than or equal to 
 be a set of integers containing
be a set of integers containing  . Suppose
. Suppose  has the property that
has the property that 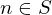 whenever every integer less than
whenever every integer less than 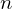 and greater than or equal to
and greater than or equal to  belongs to
belongs to  . Then,
. Then,  contains every integer greater than or equal to
contains every integer greater than or equal to 
Equivalence Relation
An equivelence relation on a set S is a set R of ordered pairs ot elements of S such that:
(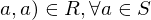 (reflexive)
(reflexive)
 implies
implies 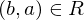 (symmetric)
(symmetric)
 and
and 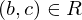 imply
imply  (transitive)
(transitive)
(
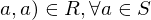 (reflexive)
(reflexive) implies
implies 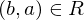 (symmetric)
(symmetric) and
and 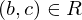 imply
imply  (transitive)
(transitive)Partition
A partition of a set  is a collection of nonempty disjoint subsets of
is a collection of nonempty disjoint subsets of  whose unions is
whose unions is  .
.
 is a collection of nonempty disjoint subsets of
is a collection of nonempty disjoint subsets of  whose unions is
whose unions is  .
.Theorem 0.6 Equivalence Classes Partition
The equivalence classes of an equivalence relation on a set  constitute a partition of
constitute a partition of  . Conversely, for any partition
. Conversely, for any partition 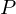 of
of  , there is an equivalence relation on
, there is an equivalence relation on  whose equivalence classes are the elements of
whose equivalence classes are the elements of 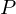
 constitute a partition of
constitute a partition of  . Conversely, for any partition
. Conversely, for any partition 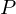 of
of  , there is an equivalence relation on
, there is an equivalence relation on  whose equivalence classes are the elements of
whose equivalence classes are the elements of 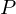
Function (Mapping)
A function (or mapping) 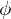 from a set
from a set 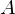 to a set
to a set 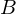 is a rule that assigns to each element
is a rule that assigns to each element  of
of 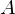 exactly one element
exactly one element 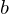 of
of 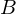 . The set
. The set 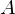 is called the domain of
is called the domain of 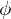 and
and 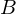 is called the range of
is called the range of 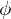 . If
. If 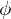 assigns
assigns 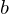 to
to  , then
, then 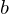 is called the image of
is called the image of  under
under 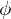 . The subset of
. The subset of 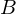 comprising all the images of elements of
comprising all the images of elements of 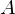 is called the image of A under
is called the image of A under 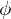 .
.
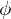 from a set
from a set 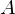 to a set
to a set 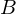 is a rule that assigns to each element
is a rule that assigns to each element  of
of 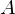 exactly one element
exactly one element 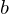 of
of 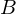 . The set
. The set 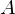 is called the domain of
is called the domain of 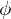 and
and 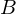 is called the range of
is called the range of 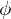 . If
. If 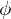 assigns
assigns 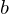 to
to  , then
, then 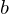 is called the image of
is called the image of  under
under 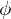 . The subset of
. The subset of 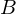 comprising all the images of elements of
comprising all the images of elements of 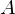 is called the image of A under
is called the image of A under 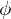 .
.Kartensatzinfo:
Autor: Squiggleart
Oberthema: Mathematics
Thema: Abstract Algebra
Schule / Uni: West Chester University
Veröffentlicht: 25.05.2011
Tags: Algebra
Schlagwörter Karten:
Alle Karten (10)
keine Schlagwörter



