Was ist die Aufgabe der Projektion?
Für die Anzeige am zweidimensionalen Ausgabegerät muß eine Abbildung (Projektion) der räumlichen,
dreidimensionalen Szene auf eine zweidimensionale Projektionsebene erfolgen.
dreidimensionalen Szene auf eine zweidimensionale Projektionsebene erfolgen.
Schritte von 3D zu 2D
- Blickwinkel festlegen
- Kameraeigentschaften festlegen (Sichtpyramide)
- Sichtpyramide normieren
- Clipping
- Auf das Sichtfenster (2D) bringen
- Kameraeigentschaften festlegen (Sichtpyramide)
- Sichtpyramide normieren
- Clipping
- Auf das Sichtfenster (2D) bringen
Definition 3D Clipping
- Anstatt Clipping der 2D-Objekte am Viewplane
- Clipping der 3D-Objekte am View-Frustum
- Clipping der 3D-Objekte am View-Frustum
Kamera - 3 wichtige Angaben
1. Wo ist die Kamera? (Viewpoint)
2. Wo guckt sie hin? (Center of interest)
3. Wo ist oben? (up Vector)
2. Wo guckt sie hin? (Center of interest)
3. Wo ist oben? (up Vector)
Welche Schritte sind bei der Projektion durchzuführen?
1. Transformation
View Frustum vereinfachen:
- achsenparalell
- zentriert im Ursprung
- in Richtung z
2. Normalisieren
- Quader in Würfel verformen und zentrieren und normieren
3. Clipping
- Clipping am Einheitswürfel
4. Projektion
Weglassen der z-Koordinate
View Frustum vereinfachen:
- achsenparalell
- zentriert im Ursprung
- in Richtung z
2. Normalisieren
- Quader in Würfel verformen und zentrieren und normieren
3. Clipping
- Clipping am Einheitswürfel
4. Projektion
Weglassen der z-Koordinate
View Koordinaten System

C = Center of Interest
P0 = Koordinaten der Kamera
g = User Up Vector
Projektionsarten
- Perspektivische Projektion
- 1 Punkt
- 2 Punkt
- 3 Punkt
- Parallel / Orthogonal
- oblique
- Cavalier
- Cabinet
- Orthograpic
- 1 Punkt
- 2 Punkt
- 3 Punkt
- Parallel / Orthogonal
- oblique
- Cavalier
- Cabinet
- Orthograpic
Wo befindet sich das Auge bei den unterschiedlichen Projektionsarten?
Perspektive: Schnittpunkt der Fluchtpunkte
Orthogonal: Im Unendlichen
Orthogonal: Im Unendlichen
Anwendungsbeispiele für die Projektionsarten
Perspektivische Projektion: Virtuelle Realität, Filme, Spiele
Orthogonale Projektion: technische Illustrationen, CAD
Orthogonale Projektion: technische Illustrationen, CAD
Vorteile / Nachteile Perspektivische P.
+ realitätsnah
+ entspricht dem normalen Sehvorgang
- Länge schwer abzuschätzen
- Ergebnis abhängig von Kamerattibuten
+ entspricht dem normalen Sehvorgang
- Länge schwer abzuschätzen
- Ergebnis abhängig von Kamerattibuten
Arten der Paralellprojektion
- Cavalier:
Blickwinkel auf die Szene = 45°
-> Längen bleiben erhalten
- Cabinet
Blickwinkel auf die Szene = 30°
-> Längen um die Hälfte verkürzt
Blickwinkel auf die Szene = 45°
-> Längen bleiben erhalten
- Cabinet
Blickwinkel auf die Szene = 30°
-> Längen um die Hälfte verkürzt
Ablauf orthogonale Projektion
1. Spiegelung an dern Z-Achse
2. Bestimmung des kanonischen Volumens (Rechteck)
3. Translation des View-Volumes in den Ursprung
4. Skalierung in Einheitswürfel
5. Clipping
6. Projektion (Abbildung auf 2D)
7. Skalierung der View-Plane auf gewünschte Fenstergröße
2. Bestimmung des kanonischen Volumens (Rechteck)
3. Translation des View-Volumes in den Ursprung
4. Skalierung in Einheitswürfel
5. Clipping
6. Projektion (Abbildung auf 2D)
7. Skalierung der View-Plane auf gewünschte Fenstergröße
Ablauf Perspektivische Projektion
1. Viewpoint in den Ursprung der Welt verschieben
(Objekte relativ mitverschieben)
2. Einfürung von Clipping View-Planes (Near+Far)
3. Skalierung der Near-Plane auf Größe der Far-Plane
4. Translation des View-Volumes in den Ursprung (nur z-Wert!)
5. Skalierung in Einheitswürfel
6. 3D-Clipping
7. Projektion
8. Skalierung auf gewünschte Fenstergröße
(Objekte relativ mitverschieben)
2. Einfürung von Clipping View-Planes (Near+Far)
3. Skalierung der Near-Plane auf Größe der Far-Plane
4. Translation des View-Volumes in den Ursprung (nur z-Wert!)
5. Skalierung in Einheitswürfel
6. 3D-Clipping
7. Projektion
8. Skalierung auf gewünschte Fenstergröße
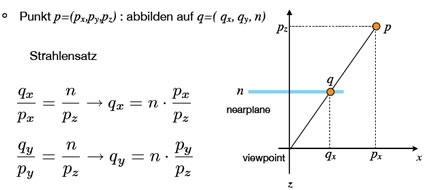
Was passiert bei der Division durch die Homogene?
Division durch w (Homogenisierung) ergibt
den projizierten Punkt in homogenen
Koordinaten.
den projizierten Punkt in homogenen
Koordinaten.
Kartensatzinfo:
Autor: dandy08
Oberthema: Design
Thema: Computergrafik
Veröffentlicht: 15.06.2010
Schlagwörter Karten:
Alle Karten (24)
keine Schlagwörter