Was ist eine Funktion der Menge A in die Menge B?
Es muss für eine Relation gelten:
Für jedes Element a∈ A gibt es genau ein Element b∈ B mit
(a,b) ∈ R
Für jedes Element a∈ A gibt es genau ein Element b∈ B mit
(a,b) ∈ R
Tags: Funktionen, Relationen
Quelle: VL 2
Quelle: VL 2
Wie schreibt man Funktionen auf?
f: A  B
B
 f(a)
f(a)
Die Funktion f bildet ein Element a ∈ A auf ein Element f (a) ∈ B ab. Dabeist A der Definitionsbereich und B der Wertebreich.
 B
B f(a)
f(a)Die Funktion f bildet ein Element a ∈ A auf ein Element f (a) ∈ B ab. Dabeist A der Definitionsbereich und B der Wertebreich.
Tags: Funktionen, Relationen
Quelle: VL 2
Quelle: VL 2
Was ist eine injektive Funktion?
Eine Funktion f: A  B heißt injenktiv, falls es keine Elemente a1, a2 ∈ A gibt mit a1
B heißt injenktiv, falls es keine Elemente a1, a2 ∈ A gibt mit a1 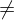 a2 und f(a1) = f(a2).
a2 und f(a1) = f(a2).
Mit anderen Worten: Auf kein Element im Wertebereich zeigt mehr als ein Pfeil.
 B heißt injenktiv, falls es keine Elemente a1, a2 ∈ A gibt mit a1
B heißt injenktiv, falls es keine Elemente a1, a2 ∈ A gibt mit a1 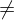 a2 und f(a1) = f(a2).
a2 und f(a1) = f(a2).Mit anderen Worten: Auf kein Element im Wertebereich zeigt mehr als ein Pfeil.
Tags: Funktionen, Relationen
Quelle: VL 2
Quelle: VL 2
Was ist eine surjektive Funktion?
Eine Funktion f: A  B heißt surjektiv, falls es für jedes b ∈ B (mindestens) ein a ∈ A gibt mit f(a) = B.
B heißt surjektiv, falls es für jedes b ∈ B (mindestens) ein a ∈ A gibt mit f(a) = B.
Mit anderen Worten: auf jedes Element im Wertebreich zeigt (mindestens) ein Pfeil.
 B heißt surjektiv, falls es für jedes b ∈ B (mindestens) ein a ∈ A gibt mit f(a) = B.
B heißt surjektiv, falls es für jedes b ∈ B (mindestens) ein a ∈ A gibt mit f(a) = B.Mit anderen Worten: auf jedes Element im Wertebreich zeigt (mindestens) ein Pfeil.
Tags: Funktionen, Relationen
Quelle: VL 2
Quelle: VL 2
Was ist eine bijektive Funktion? Welche besondere Eigenschaft hat sie?
Eine Funktion f:  heißt bijektiv, falls sie injektiv und surjektiv ist.
heißt bijektiv, falls sie injektiv und surjektiv ist.
Mit anderen Worten: auf jedes Element im Wertebereich zeigt genau ein Pfeil, d.h., es gibt eine eins-zu-eins-Zuordnung zwischen den Elementen des Definitionsbereichs und des Wertebereichs.
Die bijektiven Funktionen sind genau die invertierbaren
Funktionen. Zu einer bijektiven Funktion f : gibt es eine Umkehrfunktion
gibt es eine Umkehrfunktion 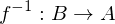 mit folgenden Eigenschaften:
mit folgenden Eigenschaften:
 (
( (a)) = a für alle a
(a)) = a für alle a  A
A
 (b)) = b für alle b
(b)) = b für alle b  B
B
 heißt bijektiv, falls sie injektiv und surjektiv ist.
heißt bijektiv, falls sie injektiv und surjektiv ist.Mit anderen Worten: auf jedes Element im Wertebereich zeigt genau ein Pfeil, d.h., es gibt eine eins-zu-eins-Zuordnung zwischen den Elementen des Definitionsbereichs und des Wertebereichs.
Die bijektiven Funktionen sind genau die invertierbaren
Funktionen. Zu einer bijektiven Funktion f :
 gibt es eine Umkehrfunktion
gibt es eine Umkehrfunktion 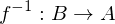 mit folgenden Eigenschaften:
mit folgenden Eigenschaften: (
( (a)) = a für alle a
(a)) = a für alle a  A
A (b)) = b für alle b
(b)) = b für alle b  B
BTags: Funktionen, Relationen
Quelle: VL 2
Quelle: VL 2
Wie notiert man eine Verknüpfung von Funktionen?
Wenn die Funktionen f:  und g:
und g:  gegeben sind, dann wird die Verknüpfung bzw. die Hintereinanderausführung mit
gegeben sind, dann wird die Verknüpfung bzw. die Hintereinanderausführung mit 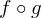 bezeichnet.
bezeichnet.

 und g:
und g:  gegeben sind, dann wird die Verknüpfung bzw. die Hintereinanderausführung mit
gegeben sind, dann wird die Verknüpfung bzw. die Hintereinanderausführung mit 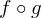 bezeichnet.
bezeichnet.
Tags: Funktionen, Relationen
Quelle: VL 2
Quelle: VL 2
Welche Bedingungen müssen für eine Äquivalenzrelation gegeben sein?
Bsp: R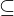 A x A
A x A
Bsp: R
 A x A
A x A1. Reflexivität: für alle a ∈ A gilt (a,a) ∈ R.
2. Transitivität: Falls für beliebige a,b,c ∈ A (a,b) ∈ R und (b,c) ∈R gilt, so muss auch (a,c) ∈ R gelten.
3. Symmetrie: Falls für beliebige a,b ∈ A (a,b) ∈ R gilt, so muss auch (b,a) ∈ R gelten.
2. Transitivität: Falls für beliebige a,b,c ∈ A (a,b) ∈ R und (b,c) ∈R gilt, so muss auch (a,c) ∈ R gelten.
3. Symmetrie: Falls für beliebige a,b ∈ A (a,b) ∈ R gilt, so muss auch (b,a) ∈ R gelten.
Tags: Relationen
Quelle: VL 2
Quelle: VL 2
Gegeben ist die Funktion f:  und
und 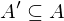 . Gib das Bild und das Urblild an!
. Gib das Bild und das Urblild an!
 und
und 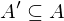 . Gib das Bild und das Urblild an!
. Gib das Bild und das Urblild an!Das Bild von A' unter der Funktion f, wenn 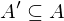 :
:
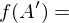 {
{  }
}
Das Urbild von B' unter der Funktion f, wenn :
:
 {
{  }
}
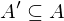 :
: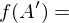 {
{  }
}Das Urbild von B' unter der Funktion f, wenn
 :
: {
{  }
}Tags: Funktionen, Relationen
Quelle: VL 2
Quelle: VL 2
Kartensatzinfo:
Autor: P-H-I-L
Oberthema: Mathematik
Thema: Mathematische Strukturen
Veröffentlicht: 13.04.2010
Schlagwörter Karten:
Alle Karten (50)
Äquivalenzklasse (1)
Funktionen (7)
Grundlagen (1)
Kreuzprodukt (1)
Leere Menge (1)
Mengen Ordnung (1)
Mengendifferenz (1)
Potenzmenge (2)
Relation (2)
Relationen (8)
Teilmenge (1)
Vereinigung (1)
VL 18.05. (10)
VL vom 4.5.10 (10)
Zahlen 04.05.10 (1)



