Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
5
Theorem 0.4 First Principle of Mathematical Induction
Let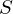 
be a set of integers containing 
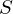. Suppose has the property that whenever some integer 
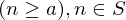, then the integer 
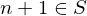. Then, 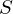contains every integer greater than or equal to .
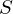be a set of integers containing . Suppose 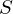has the property that whenever some integer 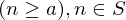, then the integer 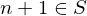. Then, 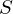contains every integer greater than or equal to .
Karteninfo:
Autor: Squiggleart
Oberthema: Mathematics
Thema: Abstract Algebra
Schule / Uni: West Chester University
Veröffentlicht: 25.05.2011