This flashcard is just one of a free flashcard set. See all flashcards!
13
Let 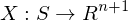 be a Vector field for
be a Vector field for 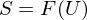 . When is X differentiable and how is
. When is X differentiable and how is 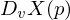 for
for 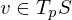 defined?
defined?
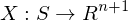 be a Vector field for
be a Vector field for 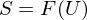 . When is X differentiable and how is
. When is X differentiable and how is 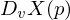 for
for 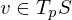 defined?
defined?X is differentiable if 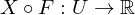 is differentiable.
is differentiable.
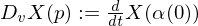
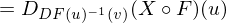
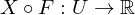 is differentiable.
is differentiable.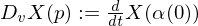
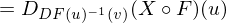
Flashcard info:
Author: Yann-Paul
Main topic: Mathematik
Topic: Differentialgeometrie123
Published: 15.11.2018


den zweiten Ausdruck verstehe ich irgendwie nicht ganz, was ist DF(u)invers?