This flashcard is just one of a free flashcard set. See all flashcards!
10
Satz über Vollständigkeit von 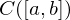
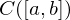
Der unendlichdimensionale normierte Raum 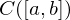 ist vollständig bezüglich
ist vollständig bezüglich
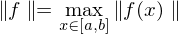
(Maximum- bzw. Supremumnorm auf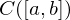 .
.
Bemerkungen
1. Bezüglich der durch das Skalarprodukt
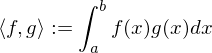
bestimmten Norm ist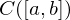 nicht vollständig.
nicht vollständig.
2. Konvergenz bezüglich des Maximum heißt auch gleichmäßige Konvergenz der Funktionenfolge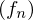 im Gegensatz zur punktweisen Konvergenz der Funktionenfolge
im Gegensatz zur punktweisen Konvergenz der Funktionenfolge 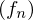 von
von

für jedes .
.
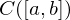 ist vollständig bezüglich
ist vollständig bezüglich 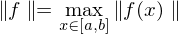
(Maximum- bzw. Supremumnorm auf
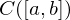 .
.Bemerkungen
1. Bezüglich der durch das Skalarprodukt
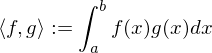
bestimmten Norm ist
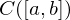 nicht vollständig.
nicht vollständig.2. Konvergenz bezüglich des Maximum heißt auch gleichmäßige Konvergenz der Funktionenfolge
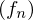 im Gegensatz zur punktweisen Konvergenz der Funktionenfolge
im Gegensatz zur punktweisen Konvergenz der Funktionenfolge 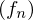 von
von 
für jedes
 .
.
