Produktions-, Entwicklungs-, und Zufallsprozesse durch Übergangsdiagramme und Matrizen beschreiben und Zustandsverktoren interpretieren.
Produktionsprozesse: Mithilfe von Matrizen lässt sich der Ablauf einer Produktion beschreiben: beispielsweise, wie sich verschiedene Produkte aus Grundelementen( also Erzeugnise aus Rohstoffen oder Enderzeugnisse aus Zwischenerzeugnissen) oder Produktionsaufträge aus einzelnen Kundenaufträgen zusammensetzen.
Entwicklungsprozesse: Man betrachtet eine Population von Individuen in verschiedenen Entwicklungsstadien, die mit gewissen Überlebenswahrscheinlichkeiten eine nächste Phase der Entwicklung erreichen, sich außerdem in bestimmten Phasen vermehren oder sterben können. In die Matrix gehen sowohl die Überlebenswahrscheinlichkeiten als auch die Reproduktionsrate als Koeffizienten ein.
Entwicklungsprozesse: Man betrachtet eine Population von Individuen in verschiedenen Entwicklungsstadien, die mit gewissen Überlebenswahrscheinlichkeiten eine nächste Phase der Entwicklung erreichen, sich außerdem in bestimmten Phasen vermehren oder sterben können. In die Matrix gehen sowohl die Überlebenswahrscheinlichkeiten als auch die Reproduktionsrate als Koeffizienten ein.
Produktions-, Entwicklungs-, und Zufallsprozesse durch Übergangsdiagramme und Matrizen beschreiben und Zustandsverktoren interpretieren.
Zufallsprozesse: Die Zustände eines Systems werden mithilfe von Zustandsvektoren beschrieben. Diese geben an, mit welcher Wahrscheinlichkeit ein bestimmtes Ereigniss zu einem bestimmten Zeitpunkt eintritt. Die zugehörigen Ereignisse (Zustände) und die Wahrscheinlichkeit für die Übergänge zwischen den Ereignissen werden graphisch mithilfe eines Übergangsdiagramms beschrieben, algebraisch mithilfe der Übergangsmatrix. Dabei wird die Übergangswahrscheinlichkeit von einem Zeitpunkt E, in einen Zustand E, in die Zeile a, der Matrix eingetragen (i-te Zeile, j-te Spalte). Da die Zustandsvektoren von Zufallsprozessen eine Wahrscheinlichkeitsverteilung beschreiben, ist die Summe der Wahrscheinlichkeiten in einer Spalte der Übergangsmatrix und in jedem Zustandsvektor immer gleich eins.
Zustände von Prozessen nach wiederholter Durchführung mithilfe der Matrizenmultiplikation berechnen und deuten, insbesondere bei zyklischen Prozessen.
Wird ein Prozess durch eine Matrix beschrieben, dann erhält man aus dem Ausgangsvektor durch Multiplizieren den Vektor des zeitlich nachfolgenden Zustandes und durch wiederholte Multiplikation mit der Matrix die darauf folgenden Zustände. Diese kann man direkt auch dadurch berechnen, dass man - gemäß dem Assoziativgesetz- zunächst die entsprechende Matrixpotenz berechnet und diese dann mit dem Ausgangsvektor multipliziert:
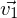 =
=  *
*  ,
, 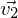 =
= 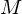 *
* 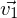 ,
, 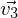 =
=  *
* 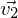 usw. oder
usw. oder 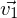 =
=  *
*  ,
,
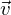 =
= ² *
² *  ,
,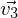 =
=  ³ *
³ *  ...
...
Gilt für irgendeine Matrixpotenz von , dass
, dass 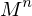 = E(Einheitsmatrix) für
= E(Einheitsmatrix) für 

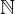 , also
, also 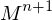 =
= , dann wird durch die Übergangsmatrix
, dann wird durch die Übergangsmatrix  ein zyklischer Prozess der Länge n beschrieben. Dies bedeutet, dass sich die Folge der Zustandsvektoren jeweils nach n Schritten wiederholt.
ein zyklischer Prozess der Länge n beschrieben. Dies bedeutet, dass sich die Folge der Zustandsvektoren jeweils nach n Schritten wiederholt.
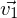 =
=  *
*  ,
, 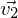 =
= 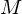 *
* 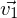 ,
, 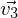 =
=  *
* 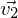 usw. oder
usw. oder 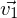 =
=  *
*  ,
,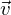 =
= ² *
² *  ,
,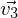 =
=  ³ *
³ *  ...
...Gilt für irgendeine Matrixpotenz von
 , dass
, dass 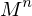 = E(Einheitsmatrix) für
= E(Einheitsmatrix) für 

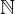 , also
, also 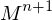 =
= , dann wird durch die Übergangsmatrix
, dann wird durch die Übergangsmatrix  ein zyklischer Prozess der Länge n beschrieben. Dies bedeutet, dass sich die Folge der Zustandsvektoren jeweils nach n Schritten wiederholt.
ein zyklischer Prozess der Länge n beschrieben. Dies bedeutet, dass sich die Folge der Zustandsvektoren jeweils nach n Schritten wiederholt.Flashcard set info:
Author: CoboCards-User
Main topic: Mathematik
Topic: Mathe-Lk
School / Univ.: MGS
City: Schwelm
Published: 19.03.2011
Tags: Kompetenzübersicht
Card tags:
All cards (5)
no tags



