Elektrischer Schwingkreis im Vergleich zur Schwingung eines Federpendels
| Elektromag. Schwingung | Federpendel | |
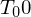 | Kondensator hat maximale Spannung, Strom = 0, mag. Feld = 0 | Kugel ist maximal ausgelenkt und bewegt sich nicht, die kinetische Energie ist null, Spannenergie ist maximal |
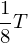 | Kondensator entlädt sich mit zunehmender Stromstärke, mag. Energie wächst, elektr. Energie nimmt ab,  | Kugel bewegt sich mit größere Geschwindigkeit, gewinnt an kinetischer Energie, vierliert an Spannenergie  |
 | Kondensator ist vollständig entladen, keine elektr. Energie mehr, Entladestrom 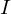 maximal, mag. Energie maximal maximal, mag. Energie maximal | Feder ist vollständig entspannt, keine Spannenergie mehr ,kinetische Energie ist maximal |
 | Induktivität der Spule bewirkt ein Weiterfließen des Stromes über die Ladungsgleichverteilung hinaus -> Kondensator lädt sich mit umgekehrten Vorzeichen auf | Die Massenträgheit treibt die Kugel über die Ruhelage hinaus -> Kugel schwingt zurück -> Spannenergie wächst wieder |
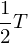 | Kondensator ist komplett entgegen gesetzt geladen | Die Kugel ist vollständig wieder zu anderen Seite ausgelenkt |
Die mechanische und elektrische Schwingung wiederholen sich nun im umgekehrter Richtung.
Dipol
Idee: Um die Frequenz des Schwingkreises zu erhöhen, muss man die Induktivität und die Kapazität im Schwingkreis reduzieren.
Beim Kondensator kann man die Flächen beliebig verkleinern und beliebig weit auseinander ziehen. Am Ende bleibt nur noch ein "gerader" Stab übrig, dieser wird als Dipol bezeichnet. Es handelt sich um einen offenen Schwingkreis.
Der Dipol dient zur Aussendung von elektromagnetischen Wellen, da das magnetische und elektrische Feld nicht mehr räumlich getrennt ist.

Beim Kondensator kann man die Flächen beliebig verkleinern und beliebig weit auseinander ziehen. Am Ende bleibt nur noch ein "gerader" Stab übrig, dieser wird als Dipol bezeichnet. Es handelt sich um einen offenen Schwingkreis.
Der Dipol dient zur Aussendung von elektromagnetischen Wellen, da das magnetische und elektrische Feld nicht mehr räumlich getrennt ist.

Dipol - zeitliche Abfolge mag./elektr. Feld
Im Dipol werden zunächste die Elektronen beschleunigt und dann abgebremst. Daraus ergibt sich eine charakteristische Verteilung von Stromstärke und Spannung längs des Dipols. An den Enden des Dipols ist die Stromstärke null, die Spannung ist zwischen den Enden maximal. In der Mitte des Dipols ist die Stromstärke am größten. Die Spannung ist null.


Versuch zum Dipol (Sender, Empfänger, Reflektor)
- HF Oszillator -> Hertz'scher Dipol dient als Sender
- weiterer Dipol mit Glühlampe (Empfänger)
- dritter Dipol als Reflektor
- Reflektor wird immer weiter von der Lampe weg bewegt
Beobachtung:
- Helligkeit nimmt mit größerem Abstand zu (Maximum bei 15-20cm)
- Helligkeit nimmt nach dem Maximum ab
- Licht erlischt bei 35cm
- 35cm nach dem Maximum wird wieder ein Maximum erreicht
Erklärung:
- Dipol auf HF Oszillator sendet hochfrequente Welle -> Empfänger Dipol -> Lampe leuchtet
- Reflektor Dipol reflektiert Welle des HF Oszillator Dipols -> stehende Welle -> Schwingungsbäuche -> Schwingungsknoten
- Bei Bewegung des Reflektors -> Lampe kommt in Schwinungsbäuche/-knoten
Beispiel:
HF Oszillator hat 434 MHz ->


Abstand der Bäuche und Knoten -> 35cm

Lecher-Leitungen offnes/geschlossenes Ende
Lecher Leitungen
Beobachtung:
Erklärung:
- zwei versilberte Messingrohe (Abstand
 2cm)* ein Ende ist an einem HF Oszillator kurzgeschlossen* an das andere Ende kann entweder offen sein oder mit einem Schleifendipol versehen sein* am Ende der Rohre steht quer ihr Richtung ein Empfangsdipol mit Lampe
2cm)* ein Ende ist an einem HF Oszillator kurzgeschlossen* an das andere Ende kann entweder offen sein oder mit einem Schleifendipol versehen sein* am Ende der Rohre steht quer ihr Richtung ein Empfangsdipol mit Lampe
Beobachtung:
- bei offenem Ende leuchtet die Lampe auf dem Empfangsdipol nicht* bei geschlossenem Ende leuchtet die Lampe auf dem Empfangsdipol
Erklärung:
- bei dem geschlossenen Ende entsteht am Ende des Rohrs ein Schwingungsknoten * bei dem offenen Ende wird die Welle reflektiert, es kommt zu einer stehenden Welle
Demodulation
Bei der Demodulation eines amplitudenmodulierten Trägers gilt es, die Hüllkurve von der Trägerschwingung zu trennen. Durch Gleichrichtung wird eine Halbschwingung des empfangenen und durch einen Schwingkreis vorselektierten, modulierten Trägers unterdrückt. Man erhält somit eine pulsierende Gleichspannung, die aus einem niederfrequeten Wechselspannungsanteil und einem hochfrequenten Wechselspannungsanteil besteht. Durch Filterung z. B. mit einem RC-Tiefpassfilter, wird der hochfrequente Anteil unterdrückt und der niederfrequente Anteil, der das ursprüngliche Signal darstellt, bleibt übrig. Dieser wird dann verstärkt und in einem Lautsprecher hörbar gemacht.


U-Rohr Herleitung der Formel


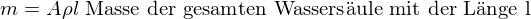
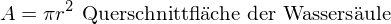
 (3)
(3)
(2) in (1) einsetzen
 (4)
(4)(3) mit (4) gleichsetzten

 (5)
(5)Ansatz
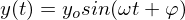 Man nimmt eine Sinusschwinung, Auslenkung bei y(0) maximal, das
Man nimmt eine Sinusschwinung, Auslenkung bei y(0) maximal, das  , da keine Verschiebung der Schwingung / beliebiger Startzeitpunkt
, da keine Verschiebung der Schwingung / beliebiger Startzeitpunkt
Ansatz mit (5) verrechnen


 Ausklammern
Ausklammern
Ein Teil der Gleichung muss null werden

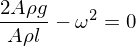

Der Strömungswiderstand sorgt in der Realität natürlich für eine gedämpfte Schwingung.

Fadenpendel - Herleitung Differentialgleichung

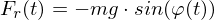
Die Geschwindigkeit nimmt mit zunehmender Auslenkung ab und steigt mit abnehmender Auslenkung. Die Geschwindigkeitsänderung bedeutet, dass die Pendelmasse eine Beschleunigung erfährt
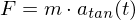
 entspricht einer Tangentialbeschleunigung
entspricht einer Tangentialbeschleunigung
Gleichsetzten und Einsetzten

Kleinstwinkelnäherung


Ansatz:

Einsetzten

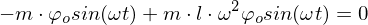

Faktorregel





Einsetzten

Umformen

Grundsätzliches Vorgehen bei Differentialgleichungen
1. Ansatz: Kräfte gleichsetzten oder den Energieansatz wählen
2. mögliche Ableitungen finden: Schwingung (-> sin/cos) / exponentielles Wachsen/Abfallen (logistisches Wachstum) e-Funktion
2.1 Gleichung nach evtl. ableiten
evtl. ableiten
3. Funktion ableiten
4. Funktion einsetzen
5. Funktion ausklammern
6. Faktorregel
7. Gleichung lösen
2. mögliche Ableitungen finden: Schwingung (-> sin/cos) / exponentielles Wachsen/Abfallen (logistisches Wachstum) e-Funktion
2.1 Gleichung nach
 evtl. ableiten
evtl. ableiten3. Funktion ableiten
4. Funktion einsetzen
5. Funktion ausklammern
6. Faktorregel
7. Gleichung lösen
Dämpfung
- Jedes ohne Energiezufuhr schwingendes System verliert mit der Zeit
 an Energie
an Energie - Dämpfung so stark -> ausreichend für eine halbe Schwingung -> aperiodische Dämpfung
Die Differentialgleichung für die ungedämpfte Schwingung lautet:

Bei der gedämpften Schwingung kommt noch die Reibungskraft
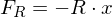 hinzu
hinzuDifferentialgleichung für die gedämpfte Schwingungen:
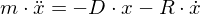
Erzwungene Schwingung
- jedes frei schwingende System kann nur mit bestimmten Frequenzen schwingen -> Eigenfrequenz wird durch die jeweiligen charakteristischen Größen festgelegt (z.B. L-C Kreis: L,C
- Ein Schwingungssystem setzt sich aus den einzelnen Eigenschwingung zusammen (Zwei Federn und Kugel dazwischen -> drei Eigenfrequenzen)
- ein Federpendel kann mit der periodischen Kraft
 angeregt werden
angeregt werden - wenn
 oder die Phasendifferenz
oder die Phasendifferenz 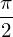 beträgt tritt der Resonanzfall ein -> Resonanzkatastrophe (Tacoma Brücke, Mikrofon und Lautsprecher im selben Raum)
beträgt tritt der Resonanzfall ein -> Resonanzkatastrophe (Tacoma Brücke, Mikrofon und Lautsprecher im selben Raum) -
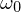 Eigenfrequenz
Eigenfrequenz - Erregerfrequenz kann nicht unendlich groß werden -> Zerstörung des Systems
- Je stärker die Dämpfung, desto geringer ist die maximale Frequenz / Amplitude
Flashcard set info:
Author: JamesBond007
Main topic: Physik
Topic: Schwingungen
Published: 07.11.2013
Card tags:
All cards (39)
no tags





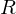 ist vernachlässigbar (
ist vernachlässigbar (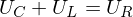 )
)


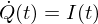







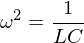


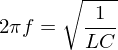





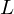 ein Strom induziert wird, wird der Transistor leitend. Und die Basis-Kollektor-Strecke wird für die Elektronen passierbar. Die verlorene Energie wird nun neu hinzugefügt.
ein Strom induziert wird, wird der Transistor leitend. Und die Basis-Kollektor-Strecke wird für die Elektronen passierbar. Die verlorene Energie wird nun neu hinzugefügt. 
 ist die Länge des Dipols
ist die Länge des Dipols

 verschoben.
verschoben. 


 zu
zu  zu
zu 

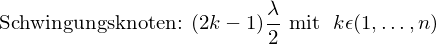


 1m)
1m)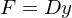





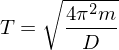


 (Rückstellkraft)
(Rückstellkraft)

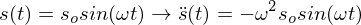



 Faktorregel
Faktorregel
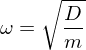






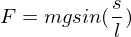


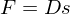

 folgt
folgt



 ´
´


 ist maximal bei der Auslenkung
ist maximal bei der Auslenkung 


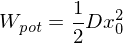
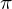 ergibt sich eine völlige Auslöschung
ergibt sich eine völlige Auslöschung


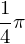 verschoben
verschoben


