Bemerkung 3.15
Sind 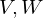 Untervektorräume von
Untervektorräume von  mit
mit  orthogonal zu
orthogonal zu  , so ist die Summe von
, so ist die Summe von  und
und  schon die direkte.
schon die direkte.
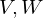 Untervektorräume von
Untervektorräume von  mit
mit  orthogonal zu
orthogonal zu  , so ist die Summe von
, so ist die Summe von  und
und  schon die direkte.
schon die direkte.Orthogonale Projektion auf 

Zu einem Untervektorraum  eines Vektorraumes
eines Vektorraumes  existiert ein orthogonales Komplement.
existiert ein orthogonales Komplement.
Die projektion ist eine Abbildung . Es ist
. Es ist  und
und  orthogonal zu
orthogonal zu  .
.
Wenn ON-Basis von
ON-Basis von  .
.
Dann ist die orth. Projektions eine Vektors auf den Unterraum
auf den Unterraum  nach Lemma 3.22
nach Lemma 3.22 
 eines Vektorraumes
eines Vektorraumes  existiert ein orthogonales Komplement.
existiert ein orthogonales Komplement.Die projektion ist eine Abbildung
 . Es ist
. Es ist  und
und  orthogonal zu
orthogonal zu  .
.Wenn
 ON-Basis von
ON-Basis von  .
.Dann ist die orth. Projektions eine Vektors
 auf den Unterraum
auf den Unterraum  nach Lemma 3.22
nach Lemma 3.22 
Prähilbertraum
Ein Prähilbertraum ist einfach ein reeler oder komplexer Vektorraum mit Skalarprodukt.
Ist der Raum vollständig, so ist er schon ein Hilbertraum.
Ist der Raum vollständig, so ist er schon ein Hilbertraum.
Darstellende Matrizen über dualen Basen
Falls  linear.
linear.  Basis von
Basis von  ,
,  Basis von
Basis von  .
.
Dann ist
Beachte das Zeilenrang = Spaltenrang.
Also folgt auch:


 linear.
linear.  Basis von
Basis von  ,
,  Basis von
Basis von  .
.Dann ist

Beachte das Zeilenrang = Spaltenrang.
Also folgt auch:


Algebraische Vielfachheit
Praktisch gesehen ist die algebraische Vielfachheit die Vielfachheiten der Nullstellen des charakteristischen Polynom.
Prinzipiell ist die algebraische Vielfachheit die Dimension der Eigenraumes zu einem Eigenwert.
Es gilt stets: Geometrische Vielfachheit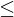 algebraische Vielfachheit.
algebraische Vielfachheit.
Prinzipiell ist die algebraische Vielfachheit die Dimension der Eigenraumes zu einem Eigenwert.
Es gilt stets: Geometrische Vielfachheit
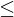 algebraische Vielfachheit.
algebraische Vielfachheit.f invariante Unterräume
1.1 Sei  also
also  . Ein UR
. Ein UR  von
von  heißt f-invariant, wenn gilt
heißt f-invariant, wenn gilt  .
.
1.2 Bemerkungen_ sind stets f-invariant.
sind stets f-invariant.
Ist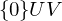 f-invariant, so ist dies ein erster Schritt zu einer "einfachen" Matrixdarstellung von
f-invariant, so ist dies ein erster Schritt zu einer "einfachen" Matrixdarstellung von  . Sei
. Sei  Basis von
Basis von  , ergänze
, ergänze  zu Basis
zu Basis  von
von  . Bzgl. dieser Basis hat
. Bzgl. dieser Basis hat  eine Matrix
eine Matrix 
1.3 Lemma: Seine vertauschbar, d.h.
vertauschbar, d.h.  . Dann sind
. Dann sind  f-invariante URe. Inbesondere sind alle Eigenräume von
f-invariante URe. Inbesondere sind alle Eigenräume von 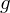 f-invariant.
f-invariant.
(Natürlich ohne Einschränkungen: Also alle Eigenräume von sind g-invariant.
sind g-invariant.
 also
also  . Ein UR
. Ein UR  von
von  heißt f-invariant, wenn gilt
heißt f-invariant, wenn gilt  .
.1.2 Bemerkungen_
 sind stets f-invariant.
sind stets f-invariant.Ist
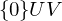 f-invariant, so ist dies ein erster Schritt zu einer "einfachen" Matrixdarstellung von
f-invariant, so ist dies ein erster Schritt zu einer "einfachen" Matrixdarstellung von  . Sei
. Sei  Basis von
Basis von  , ergänze
, ergänze  zu Basis
zu Basis  von
von  . Bzgl. dieser Basis hat
. Bzgl. dieser Basis hat  eine Matrix
eine Matrix 
1.3 Lemma: Seine
 vertauschbar, d.h.
vertauschbar, d.h.  . Dann sind
. Dann sind  f-invariante URe. Inbesondere sind alle Eigenräume von
f-invariante URe. Inbesondere sind alle Eigenräume von 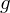 f-invariant.
f-invariant.(Natürlich ohne Einschränkungen: Also alle Eigenräume von
 sind g-invariant.
sind g-invariant.Tags:
Quelle: Skript Scheiderer BII I §1 Hauptaumzerlegung Def.1.1, Bem.1.2
Quelle: Skript Scheiderer BII I §1 Hauptaumzerlegung Def.1.1, Bem.1.2
Nilpotent, Nilpotenzindex

 heißt nilpotent, falls
heißt nilpotent, falls  .
.Das kleinste solche
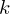 heißt der Nilpotenzindex von
heißt der Nilpotenzindex von  . Analog für quadratische Matrix.
. Analog für quadratische Matrix.1.5 Beispiel: Sind
 also quadratische Matrizen und dazu ähnlich also
also quadratische Matrizen und dazu ähnlich also  , so:
, so: nilpotent
nilpotent  nilpotent.
nilpotent.(Denn: Sind
 ähnlich, ex.
ähnlich, ex.  mit
mit  .
.  Dann ist
Dann ist  .
.Mit Satz 1.6:
 ist nilpotent
ist nilpotent  zu einer Matrix mit oberer Dreiecksgestallt mit nur Nullen auf der Diagonalen.
zu einer Matrix mit oberer Dreiecksgestallt mit nur Nullen auf der Diagonalen.1.7 Korollar
 in nilpotent
in nilpotent  .
.1.8 Lemma stop

a. Es gibt eine Zahl
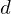 mit
mit  , so dass gilt:
, so dass gilt:(1)...
Tags:
Quelle: Skript Scheiderer BII, I Strukturtheorie von Endo, §1 Definition 1.4
Quelle: Skript Scheiderer BII, I Strukturtheorie von Endo, §1 Definition 1.4
Hauptraumzerlegung-Vorbereitungskorollar
1.9 Korollar (aus 1.8)

Setze ,
,
 .
.
(a) und
und  sind f-invariant
sind f-invariant
(b)
(c) hat char. Pol.
hat char. Pol.  und
und  ist kein EW von
ist kein EW von 

Setze
 ,
, .
.(a)
 und
und  sind f-invariant
sind f-invariant(b)

(c)
 hat char. Pol.
hat char. Pol.  und
und  ist kein EW von
ist kein EW von 
Hauptraum
 dann
dann für
für 
der Hauptraum (oder verallgemeinerte Eigenraum) von
 zum Wert
zum Wert 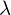 . Dies ist ein f-invarianter UR von
. Dies ist ein f-invarianter UR von  mit einem f-invarianten Komplement (nämlich dem
mit einem f-invarianten Komplement (nämlich dem  aus 1.9)
aus 1.9)Satz über die Hauptraumzerlegung
1.11 Satz
 , es zerfalle
, es zerfalle  in Linearfaktoren (
in Linearfaktoren ( , paarweise verschieden).
, paarweise verschieden).
(a)
(b)
(c) ist f-invariant und
ist f-invariant und  ist nilpotent.
ist nilpotent.
Beweise (b),(c) siehe 1.9
(a) folgt aus Lemme 1.12
 , es zerfalle
, es zerfalle  in Linearfaktoren (
in Linearfaktoren ( , paarweise verschieden).
, paarweise verschieden).(a)

(b)

(c)
 ist f-invariant und
ist f-invariant und  ist nilpotent.
ist nilpotent.Beweise (b),(c) siehe 1.9
(a) folgt aus Lemme 1.12
Geometrische Vielfachheit
Für  und
und  Eigenwert von
Eigenwert von  ist die gemometrische Vielfachheit
ist die gemometrische Vielfachheit 
Die geometrische Vielfachheit ist dagegen definiert als Dimension des Eigenraums
Insbesondere gilt . Denn
. Denn
 und
und  Eigenwert von
Eigenwert von  ist die gemometrische Vielfachheit
ist die gemometrische Vielfachheit 
Die geometrische Vielfachheit ist dagegen definiert als Dimension des Eigenraums
Insbesondere gilt
 . Denn
. Denn Jordan-Chevally Zerlegung
 zerfalle in Linearfaktoren
zerfalle in Linearfaktoren 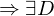 diagonalisierbar,
diagonalisierbar,  nilpotent mit
nilpotent mit  und
und  .
.Endomorphismus
Ein Endomorphismus ist eine lineare Abbildung, ein Homomorhpismus von einem Vektorraum in sich selbst.
Also für
für  ein
ein  -Vektorraum.
-Vektorraum.
Ist dazu ein Isomorphismus, so nennt man
dazu ein Isomorphismus, so nennt man  einen Automorphismus.
einen Automorphismus.
Die Menge aller Homomorphismen von in
in  ist ein Gruppe i.Z.
ist ein Gruppe i.Z.  .
.
Also
 für
für  ein
ein  -Vektorraum.
-Vektorraum.Ist
 dazu ein Isomorphismus, so nennt man
dazu ein Isomorphismus, so nennt man  einen Automorphismus.
einen Automorphismus.Die Menge aller Homomorphismen von
 in
in  ist ein Gruppe i.Z.
ist ein Gruppe i.Z.  .
.Eigenraum
Der Eigenraum ist der durch die Eigenvektoren eines Endomorhpismus aufgespannte Untervektorraum.
Tags:
Quelle: Wikipedia
Quelle: Wikipedia
Diagonalisierbarkeit einer Matrix 

Ist eine Matrix  diagonalisierbar, existiert eine Diagonalmatrix
diagonalisierbar, existiert eine Diagonalmatrix  für die die Ähnlichkeitsbedingung erfüllt ist:
für die die Ähnlichkeitsbedingung erfüllt ist:

Äquivalent: (Vielleicht selbst zu zeigen!?)
Dies ist genau dann wenn: (a) char. Pol. vollständig in Linearfaktoren zerfällt und (b) für alle
für alle 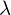 also Eigenwerte von
also Eigenwerte von  .
.
 diagonalisierbar, existiert eine Diagonalmatrix
diagonalisierbar, existiert eine Diagonalmatrix  für die die Ähnlichkeitsbedingung erfüllt ist:
für die die Ähnlichkeitsbedingung erfüllt ist:
Äquivalent: (Vielleicht selbst zu zeigen!?)
Dies ist genau dann wenn: (a) char. Pol. vollständig in Linearfaktoren zerfällt und (b)
 für alle
für alle 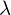 also Eigenwerte von
also Eigenwerte von  .
.Eigenschaften einer Äquivalenzrelation
1. Reflexivität: Das betrachtete Ding  ist relativ zu sich selbst, also zu
ist relativ zu sich selbst, also zu 
2. Symmetrie: Wenn das Ding zu
zu  relativ ist, so ist
relativ ist, so ist  auch relativ zu
auch relativ zu 
3. Transitivität: Wenn das Ding zu
zu  relativ ist und das Ding
relativ ist und das Ding  relativ zu
relativ zu  ist, dann ist das Ding
ist, dann ist das Ding  auch relativ zu
auch relativ zu 
Vorsicht
Es gilt nicht: aus 2. und 3. folgt 1.
Also FALSCH ist weil Symmetrisch ist
Symmetrisch ist  und dann ist
und dann ist  also
also  also ist
also ist  auch reflexiv und deshalb Äquivalenzrelation.
auch reflexiv und deshalb Äquivalenzrelation.
 ist relativ zu sich selbst, also zu
ist relativ zu sich selbst, also zu 
2. Symmetrie: Wenn das Ding
 zu
zu  relativ ist, so ist
relativ ist, so ist  auch relativ zu
auch relativ zu 
3. Transitivität: Wenn das Ding
 zu
zu  relativ ist und das Ding
relativ ist und das Ding  relativ zu
relativ zu  ist, dann ist das Ding
ist, dann ist das Ding  auch relativ zu
auch relativ zu 
Vorsicht
Es gilt nicht: aus 2. und 3. folgt 1.
Also FALSCH ist weil
 Symmetrisch ist
Symmetrisch ist  und dann ist
und dann ist  also
also  also ist
also ist  auch reflexiv und deshalb Äquivalenzrelation.
auch reflexiv und deshalb Äquivalenzrelation.Sei  und
und 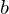 eine Bilinearform auf
eine Bilinearform auf  . Wann ist
. Wann ist 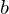 nicht ausgeartet?
nicht ausgeartet?
 und
und 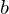 eine Bilinearform auf
eine Bilinearform auf  . Wann ist
. Wann ist 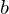 nicht ausgeartet?
nicht ausgeartet?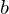 ist nicht ausgeartet, falls eine der Bedingungen gilt:
ist nicht ausgeartet, falls eine der Bedingungen gilt:

!!

für eine (d.h. für jede) Basis
 von
von  ist
ist 
Was bedeutet  ?
?
 ?
? kongruent
kongruent 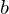 modulo
modulo  .
. bedeutet
bedeutet  .
.Also der Rest von
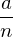 ist gleich dem Rest von
ist gleich dem Rest von  .
. Restklassenkörper. Was ist
Restklassenkörper. Was ist  ?
?Gebe die Elemente der Menge
 konkret an.
konkret an.Ist
 überhaupt ein Körper?
überhaupt ein Körper?Antwort: 



Wie viele Elemente hat ein n-dimensionaler  -Vektorraum über dem endlichen,
-Vektorraum über dem endlichen, 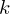 -elementigen Körper
-elementigen Körper  ?
?
 -Vektorraum über dem endlichen,
-Vektorraum über dem endlichen, 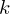 -elementigen Körper
-elementigen Körper  ?
? 
(Satz über die Anzalh der Elemente eines endlichen Vektorraumes.)
Was sagt der Satz über die Anzahl der Elemente einse endlichen Vektorraumes?
Ein n-dimensionaler  -Vektorraum über dem endlichen, k-elementigen Körper hat genau
-Vektorraum über dem endlichen, k-elementigen Körper hat genau  .
.
 -Vektorraum über dem endlichen, k-elementigen Körper hat genau
-Vektorraum über dem endlichen, k-elementigen Körper hat genau  .
.Anzahl der Vektoren einer Nebenklasse. Wieviele Vektoren hat eine Nebenklasse?
Nebenklassen sind immer abhängig von dem jeweiligen Untervektorraum  .
.
Grundsätzlich macht diese Frage nur sinn, wenn eine endliche Menge betrachtet wird. Irgendeine Anzahl an Elementen wird
betrachtet wird. Irgendeine Anzahl an Elementen wird  dann ja haben, wenn es endlich. Diese Zahl nennen wir einfach
dann ja haben, wenn es endlich. Diese Zahl nennen wir einfach 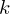 .
.
 selbst ist zu sich ist eine Nebenklasse, nämlich die Nebenklasse
selbst ist zu sich ist eine Nebenklasse, nämlich die Nebenklasse  .
.
Diese Nebenklasse hat die gleiche Anzahl an Element wie natürlich. Also genau
natürlich. Also genau  . (Nach dem Satz über die Anzahl von Elementen eins Vektoraumes)
. (Nach dem Satz über die Anzahl von Elementen eins Vektoraumes)
Wann könnte jetzt auf die Idee kommen, zu vermuten, dass auch jede äquivalente Nebenklasse gleichviele Elemente wie hat, und man könnte im ersten Versuch mal versuchen ein Bijektive Abbildung zwischen
hat, und man könnte im ersten Versuch mal versuchen ein Bijektive Abbildung zwischen  und
und  zu konstruieren. Klappt das, so ist klar, dass
zu konstruieren. Klappt das, so ist klar, dass  und
und  gleichmächtig sein müssen.
gleichmächtig sein müssen.
Das klappt mit . Denn die Surjektivitöt folgt aus der Definition der Nebenklasse und die Injetivität ist einfach mit
. Denn die Surjektivitöt folgt aus der Definition der Nebenklasse und die Injetivität ist einfach mit  .
.
 .
.Grundsätzlich macht diese Frage nur sinn, wenn eine endliche Menge
 betrachtet wird. Irgendeine Anzahl an Elementen wird
betrachtet wird. Irgendeine Anzahl an Elementen wird  dann ja haben, wenn es endlich. Diese Zahl nennen wir einfach
dann ja haben, wenn es endlich. Diese Zahl nennen wir einfach 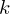 .
. selbst ist zu sich ist eine Nebenklasse, nämlich die Nebenklasse
selbst ist zu sich ist eine Nebenklasse, nämlich die Nebenklasse  .
.Diese Nebenklasse hat die gleiche Anzahl an Element wie
 natürlich. Also genau
natürlich. Also genau  . (Nach dem Satz über die Anzahl von Elementen eins Vektoraumes)
. (Nach dem Satz über die Anzahl von Elementen eins Vektoraumes)Wann könnte jetzt auf die Idee kommen, zu vermuten, dass auch jede äquivalente Nebenklasse gleichviele Elemente wie
 hat, und man könnte im ersten Versuch mal versuchen ein Bijektive Abbildung zwischen
hat, und man könnte im ersten Versuch mal versuchen ein Bijektive Abbildung zwischen  und
und  zu konstruieren. Klappt das, so ist klar, dass
zu konstruieren. Klappt das, so ist klar, dass  und
und  gleichmächtig sein müssen.
gleichmächtig sein müssen.Das klappt mit
 . Denn die Surjektivitöt folgt aus der Definition der Nebenklasse und die Injetivität ist einfach mit
. Denn die Surjektivitöt folgt aus der Definition der Nebenklasse und die Injetivität ist einfach mit  .
. Abbildung,
Abbildung,  Darstellende Matrix von
Darstellende Matrix von  . Was ist
. Was ist  , was ist
, was ist  ?
?Die Spaltenvektoren von A sind die Bilder der Basisverktoren.

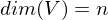

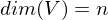
Wie stehen Kern einer Funktion f und ihre Injektivität zusammen?
f ist injektiv gdw. ker(f)=0
Die über dem Ring der Polynome eingeführte Multiplikation ist definiert als...
 unendliche Folge mit endlich vielen von Null verschiedenen Elementen
unendliche Folge mit endlich vielen von Null verschiedenen Elementen
Das
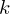 -te Glied von
-te Glied von  errechnet sich wie folgt:
errechnet sich wie folgt:
Kartensatzinfo:
Autor: attila.rufius
Oberthema: Mathematik
Thema: Algebra
Veröffentlicht: 01.03.2010
Schlagwörter Karten:
Alle Karten (53)
keine Schlagwörter



 gilt
gilt







 ist definiert als
ist definiert als 


 orthogonal zu
orthogonal zu 

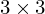 -Matrix
-Matrix 


 so existiert eine Zahl
so existiert eine Zahl  mit
mit



 .
. 





 .
.
 von
von  bzw. von
bzw. von  das sog. "Absolutglied".
das sog. "Absolutglied". von
von  bzw. von
bzw. von  heißt "Lineares Glied".
heißt "Lineares Glied".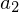 von
von 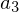 von
von  ?
?

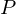 definiert
definiert


