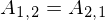Was passiert mit der Verdrillung, wenn die Querkraft durch den Schubmittelpkt geht?
Wie kann man die Querkaft evtl. beeinflussen, dass diese durch den Schubmittelpkt geht?
Wie kann man die Querkaft evtl. beeinflussen, dass diese durch den Schubmittelpkt geht?
1) Verdrillung = 0
2) - wenn Verdrillung > 0, dann muss Q nach links auf der Achse verschoben werden
- wenn Verdrillung < 0, dann Q nach rechts verschieben
2) - wenn Verdrillung > 0, dann muss Q nach links auf der Achse verschoben werden
- wenn Verdrillung < 0, dann Q nach rechts verschieben
Warum benötigt ein Stabbalkenelement mit einem quadratischen Ansatz 3 Knoten, ein Bernoullibalken aber nur 2 Knoten?
Ein Bernoulli-Balken hat zwei Knoten mit je zwei Freiwerten. Demzufolge besitzt er 4 Freiwerte und man benötigt 4 Randbedingungen um ihn eindeutig zu bestimmen. Die Ansatzfunktion ist deshalb bei 2 Knoten schon vom Grad 3.

Ein Stabelement hat nur einen Freiwert pro Knoten. Für einen quadratische Ansatz werden jedoch 3 Freiwerte benötigt. => 3 Knoten nötig.

Ein Stabelement hat nur einen Freiwert pro Knoten. Für einen quadratische Ansatz werden jedoch 3 Freiwerte benötigt. => 3 Knoten nötig.
Welche Formen der Linearität kennen Sie in der Statik und wo spielen Sie eine Rolle?
In der Theorie 1. Ordnung: Hierbei spielt die Linearität bei Verformungen und Verschiebungen eine wichtige Rolle. Unter der Annahme, dass Verformungen sehr klein gegenüber der Gesamtlänge und Größe des Gegenstandes sind, kann man von einer Proportionalität der Spannungen und Dehnung gegenüber den aufgebrachten Kräften ausgehen.
Aus der Linearität folgen das Proportionalitätsprinzip zwischen Verformungen/Spannungen und Kräften und das Superpositionsprinzip für die lineare Überlagerung von Verformungen/Spannungen und Kräften.
Aus der Linearität folgen das Proportionalitätsprinzip zwischen Verformungen/Spannungen und Kräften und das Superpositionsprinzip für die lineare Überlagerung von Verformungen/Spannungen und Kräften.
Symmetrisches und antisymmetrisches Halbmodell. [Siehe Antwort für Skizze!!]
a) Skizze
b) Die Ebene sei nun um den Winkel gekippt. Welches Halbmodell würden Sie zur Lösung bezogen auf die Gewichtskraft einsetzen?
a) Skizze
b) Die Ebene sei nun um den Winkel gekippt. Welches Halbmodell würden Sie zur Lösung bezogen auf die Gewichtskraft einsetzen?
a) 
zum antisymm. Halbmodell:
Keine Feder an der linken Seite. Ferdersteifigkeit spielt hier keine Rollen, da sich beider Wage im gleichen Tackt bewegen.
zum symm. Halbmodell:
Doppelte Federsteifigkeit bei Halbierung der Federlänge und symmetrischem Aufbau.
b) Das symmetrische Halbmodell.

zum antisymm. Halbmodell:
Keine Feder an der linken Seite. Ferdersteifigkeit spielt hier keine Rollen, da sich beider Wage im gleichen Tackt bewegen.
zum symm. Halbmodell:
Doppelte Federsteifigkeit bei Halbierung der Federlänge und symmetrischem Aufbau.
b) Das symmetrische Halbmodell.
Was sind Vor- und Nachteile von Spindelantrieben zum Aufbringen von statischen Belastungen?
Vorteile:
- extrem langsame Verformungs- und Dehngeschwindigkeiten möglich (bspweise bei der Untersuchung von Knick- und Beulvorgängen)
- weitgehende Wartungsfreiheit, gute Regelbarkeit und mechanische Selbsthemmung beim Ausschalten
- breite Angebotspalette an Verstellgeschwindigkeiten und Kraftbereichen
Nachteil:
- Verstellvorgänge mit hoher Dynamik lassen sich wegen des Getriebes nicht realisieren
- extrem langsame Verformungs- und Dehngeschwindigkeiten möglich (bspweise bei der Untersuchung von Knick- und Beulvorgängen)
- weitgehende Wartungsfreiheit, gute Regelbarkeit und mechanische Selbsthemmung beim Ausschalten
- breite Angebotspalette an Verstellgeschwindigkeiten und Kraftbereichen
Nachteil:
- Verstellvorgänge mit hoher Dynamik lassen sich wegen des Getriebes nicht realisieren
Gegeben sei die allgemeine Lösung einer Differentialgleichung q(t)=qh(t)+qp(t).
Welcher der beiden Teile spielt in einem System mit bzw. ohne Dämpfung in der Einschwingphase, … und stationären Phase die größte Bedeutung?
Welcher der beiden Teile spielt in einem System mit bzw. ohne Dämpfung in der Einschwingphase, … und stationären Phase die größte Bedeutung?
mit Dämpfung:
Einschwingphase => Homogene Lösung spielt entscheidende Rolle
Stationäre Phase => Partikuläre Lösung (die Homogene Lösung wird "weggedämpft"!)
ohne Dämpfung:
Einschwingphase => Homogene Lösung spielt entscheidende Rolle
Stationäre Phase => sowohl Homogene Lösung, als auch die Partikuläre Lösung (die Homogene Lösung wird nicht "weggedämpft"!)
Einschwingphase => Homogene Lösung spielt entscheidende Rolle
Stationäre Phase => Partikuläre Lösung (die Homogene Lösung wird "weggedämpft"!)
ohne Dämpfung:
Einschwingphase => Homogene Lösung spielt entscheidende Rolle
Stationäre Phase => sowohl Homogene Lösung, als auch die Partikuläre Lösung (die Homogene Lösung wird nicht "weggedämpft"!)
Gegeben sei folgende Lösung einer Differentialgleichung:
q(t) = aic * cos(ωt) + ais * sin(ωt) + qp(t) (hier stark vereinfacht!)
a) Markieren Sie die homogene Lösung?
b) Welche Bedeutung haben die Koeffizienten ais und aic?
c) Welcher Teil der Lösung wird durch die Randbedingungen beeinflusst?
d) Können Sie keinen, einen oder beide Koeffizienten direkt ohne Rechung bestimmen (Anregung war auch gegeben)? Begründung zählt.
q(t) = aic * cos(ωt) + ais * sin(ωt) + qp(t) (hier stark vereinfacht!)
a) Markieren Sie die homogene Lösung?
b) Welche Bedeutung haben die Koeffizienten ais und aic?
c) Welcher Teil der Lösung wird durch die Randbedingungen beeinflusst?
d) Können Sie keinen, einen oder beide Koeffizienten direkt ohne Rechung bestimmen (Anregung war auch gegeben)? Begründung zählt.
a) aic * cos(ωt) + ais * sin(ωt)
b) hängen von Randbedingungen ab
c) nur der homogene Teil
d) partikulärer Teil kann direkt, ohne Rechnung vom Erregungsimpuls ausgehend bestimmt werden
b) hängen von Randbedingungen ab
c) nur der homogene Teil
d) partikulärer Teil kann direkt, ohne Rechnung vom Erregungsimpuls ausgehend bestimmt werden
Gegeben sei folgende Lösung einer Differentialgleichung:
q(t) = F/m * V * cos(Ω*t-ϕ)
und ein Diagramm mit zwei Kurven
a) Was versteht man unter dem Verstärkungsfaktor und wie groß ist er in diesem Beispiel?
b) Was versteht man unter der Phasenverschiebung und wie groß ist sie in diesem Beispiel?
c) Was versteht man unter der Amplitude der stationären Lösung und wie groß ist sie in diesem Beispiel?
q(t) = F/m * V * cos(Ω*t-ϕ)
und ein Diagramm mit zwei Kurven
a) Was versteht man unter dem Verstärkungsfaktor und wie groß ist er in diesem Beispiel?
b) Was versteht man unter der Phasenverschiebung und wie groß ist sie in diesem Beispiel?
c) Was versteht man unter der Amplitude der stationären Lösung und wie groß ist sie in diesem Beispiel?
a) V
b) Phi in der cos-Funktion
c) F/m
b) Phi in der cos-Funktion
c) F/m
Was versteht man unter der Theorie 2. Ordnung? Was ist dann bei der Berechnung und bei der Auswertung der Ergebnisse zu beachten?
Berechnung von statischen Problemen mit Hilfe nichtlinearer Zusammenhänge. Es gilt zu beachten, dass Ergebnisse nicht zwangsläufig der Realität entsprechen müssen, da es in der Realität Begrenzungen für gewisse Probleme gibt (z.Bsp. keine unendliche Auslenkung, etc. )
Nichtlinearität!
Nichtlinearität!
Durch welches Produkt wir die virtuelle Arbeit bei der Methode der Finiten Elemente üblicherweise gebildet? Wie heißt dieses Prinzip?
Die virtuelle Arbeit entsteht durch die Multiplikation von tatsächlichen Kräften mit gedachten – virtuellen – Verschiebungen.
=> obergeordnet: Prinzip der virtuellen Arbeit (PvA)
Vgl.: Skript Diskretisierung, S. 4 oben
=> Als Unterart auch das Prinzip der virtuellen Verschiebungen:
(Vgl.: Skript Diskretisierung, S. 5 mitte)
Multipliziert man die virtuellen Verschiebungen mit den tatsächlichen Kräften, so wendet man eine Unterart des Prinzips der virtuellen Arbeit an, nämlich das Prinzip der virtuellen Verschiebungen.
=> obergeordnet: Prinzip der virtuellen Arbeit (PvA)
Vgl.: Skript Diskretisierung, S. 4 oben
=> Als Unterart auch das Prinzip der virtuellen Verschiebungen:
(Vgl.: Skript Diskretisierung, S. 5 mitte)
Multipliziert man die virtuellen Verschiebungen mit den tatsächlichen Kräften, so wendet man eine Unterart des Prinzips der virtuellen Arbeit an, nämlich das Prinzip der virtuellen Verschiebungen.
Welches sind die primären Ergebnisse einer FEM-Berechnung? Geben Sie mit einer kurzen Formel an, wie diese Ergebnisse erhalten werden.
Man erhält Verschiebungen/ Verformungen:
- unbekannten Knotenfreiwerte
- unbekannte Lagerreaktionen
K: Steifigkeitsmartix
z: Knotenfreiwerte
P: Lastspalte
K*z=P
Arbeitsgleichung:
δW = 0
(Prinzip der virtuellen Arbeit!)
Vgl.: Skript Diskretisierung, S. 67 ff (Kapitel 7)
- unbekannten Knotenfreiwerte
- unbekannte Lagerreaktionen
K: Steifigkeitsmartix
z: Knotenfreiwerte
P: Lastspalte
K*z=P
Arbeitsgleichung:
δW = 0
(Prinzip der virtuellen Arbeit!)
Vgl.: Skript Diskretisierung, S. 67 ff (Kapitel 7)
Welche sind die sekundären Ergebnisse einer FEM-Berechnung? Geben Sie auch hierfür kurze Formeln an.
Längskräfte, Querkräfte, Momente und Spannungen
Spannungen: Sie müssen mit einer Nachlaufrechung aus der Differentiation der Verschiebungsansätze ermittelt werden und sind somit ungenauer.
Hooksches Gesetz: σ = Eε
Vgl.: Skript Diskretisierung, S. 2
Spannungen: Sie müssen mit einer Nachlaufrechung aus der Differentiation der Verschiebungsansätze ermittelt werden und sind somit ungenauer.
Hooksches Gesetz: σ = Eε
Vgl.: Skript Diskretisierung, S. 2
Welche Bedeutung hat eine singuläre Steifigkeitsmatrix in der Statik? Wodurch ist sie charakterisiert?

Starrkörperbewegung:
Für die Statik heißt dies, dass die Freiwerte nicht gebunden sind und somit auch keine Wechselwirkung mit anderen Freiwerten haben.
Charakteristikum einer solchen singulären Matrix => det(K)=0
- singulär
- nicht Invertierbar
- GLS nicht Lösbar
Was sind die Vorteile der linearen Theorie der Statik?
Lange Antwort:
Vorteile einer linearen Theorie (Theorie 1. Ordnung) in der Statik:
1. Gleichgewicht kann an der unverformten Struktur angesetzt werden, denn die Verschiebungen sollen klein sein gegenüber den Abmessungen des Tragwerks.
2. Verformungen und Spannungen sind proportional zur Belastung:
Wenn P →σ, dann 2P→2σ; n-fache Last → n-fache Spannungen und Verformungen.
3. Es gilt das Superpositionsgesetz (Überlagerungsgesetz) für Lastfälle:
Wenn P1→ v1; σ 1 und P2→v2 , σ 2, dann (P1 + P2) → (v1 + v2); (σ 1 + σ 2).
Vgl. Statik I Skript, S. 34
Kurze Antwort:
1. Kleine Verformungen: Verformungen und Verschiebungen sind klein gegenüber den Abmessungen des Tragwerks:
ε<<L
2. Proportionalität: Verformungen (ε) und Spannungen (σ) sind proportional zur Belastung (P):
ε~P & σ~P
3. Superposition:
(P1 + P2) ~ (ε 1 + ε 2); (σ 1 + σ 2)
Vorteile einer linearen Theorie (Theorie 1. Ordnung) in der Statik:
1. Gleichgewicht kann an der unverformten Struktur angesetzt werden, denn die Verschiebungen sollen klein sein gegenüber den Abmessungen des Tragwerks.
2. Verformungen und Spannungen sind proportional zur Belastung:
Wenn P →σ, dann 2P→2σ; n-fache Last → n-fache Spannungen und Verformungen.
3. Es gilt das Superpositionsgesetz (Überlagerungsgesetz) für Lastfälle:
Wenn P1→ v1; σ 1 und P2→v2 , σ 2, dann (P1 + P2) → (v1 + v2); (σ 1 + σ 2).
Vgl. Statik I Skript, S. 34
Kurze Antwort:
1. Kleine Verformungen: Verformungen und Verschiebungen sind klein gegenüber den Abmessungen des Tragwerks:
ε<<L
2. Proportionalität: Verformungen (ε) und Spannungen (σ) sind proportional zur Belastung (P):
ε~P & σ~P
3. Superposition:
(P1 + P2) ~ (ε 1 + ε 2); (σ 1 + σ 2)
Wann kann die lineare Theorie der Statik nicht mehr angewandt werden?
Vorraussetzung für die lineare Theorie:
Lineare Theorie erfordert, dass alle Beziehungen zwischen auftretenden Größen linear sind.
Es folgt: Sobald die Beziehungen zwischen den auftretenden Größen nicht mehr linear sind.
z.Bsp. Drehung eines Stabes => Auftretender Sinus ist bei großen Drehungen nicht mehr linear => Folglich gilt nur bei kleinen Drehungen die lineare Theorie.
Vgl. Statik I Skript, S. 35
Lineare Theorie erfordert, dass alle Beziehungen zwischen auftretenden Größen linear sind.
Es folgt: Sobald die Beziehungen zwischen den auftretenden Größen nicht mehr linear sind.
z.Bsp. Drehung eines Stabes => Auftretender Sinus ist bei großen Drehungen nicht mehr linear => Folglich gilt nur bei kleinen Drehungen die lineare Theorie.
Vgl. Statik I Skript, S. 35
Ein gerader Kragbalken ist mit einer Drucklast P am Kragende belastet.
a) Skizzieren Sie den Zusammenhang zwischen der Querauslenkung des Kragendes δ und der Drucklast P in einem Diagramm P(δ) sowie die kritische Drucklast ist Pkrit.
b) Zeichnen Sie ein entsprechendes zweites Diagramm für den Fall, dass der Kragbalken leicht gekrümmt ist.
a) Skizzieren Sie den Zusammenhang zwischen der Querauslenkung des Kragendes δ und der Drucklast P in einem Diagramm P(δ) sowie die kritische Drucklast ist Pkrit.
b) Zeichnen Sie ein entsprechendes zweites Diagramm für den Fall, dass der Kragbalken leicht gekrümmt ist.

a) Generell: Es handelt sich um eine nichtlineare Beziehung.
Warum Pkrit ?
Sobald Pkrit erreicht wurde knickt der Stab schlagartig! Es gibt auf Grund fehlender Querkraft (Q=0) keine vorherige Ausbiegung. Die Auslenkung ist dann unendlich groß.
Der Sachverhalt wird auch im Skript anschaulich dargestellt (dieser Fall wird durch Q/ Pkrit = 0 dargestellt): Statik II, S.44
b) Erklärung: Leichte Krümmung wird durch eine zusätzliche Querkraft erreicht. Die Knickung tritt nicht schlagartig auf, sondern kündigt sich durch vorherige Ausbiegung an. Nach erreichen der Kritischen Last knickt dann dieser Stab allerdings auch!
Leicht gekrümmter Kragbalken unter Zuglast:
a) Wie ändert sich die Krümmung eines leicht gekrümmten Kragbalkens wenn statt der Drucklast eine Zugkraft am Kragende aufgebracht wird?
b) Gibt es in diesem Fall nach der Theorie 2. Ordnung ebenfalls eine kritische Last?
a) Wie ändert sich die Krümmung eines leicht gekrümmten Kragbalkens wenn statt der Drucklast eine Zugkraft am Kragende aufgebracht wird?
b) Gibt es in diesem Fall nach der Theorie 2. Ordnung ebenfalls eine kritische Last?

a) Der Balken wird gerade gezogen.
b) Eine kritische Last gibt es nicht! Auslenkung und Beanspruchung (Moment) im Fall des Zuges kleiner als von der linearen Theorie vorausgesagt.
Vgl. Statik II Skript, S. 46
Durch welche Modelltypen bzw. Methoden der Mechanik (z.B. Mehrkörpersysteme (MKS), kontinuierliche Systeme (KOS), Finite-Elemente-Methode (FEM)) werden folgende Probleme am besten modelliert?
a) Mehrgliedriger Roboterarm
b) Schwingungsverhalten einer Fahrzeugkarosserie
c) Schwingungsverhalten einer Gitarrenseite
a) Mehrgliedriger Roboterarm
b) Schwingungsverhalten einer Fahrzeugkarosserie
c) Schwingungsverhalten einer Gitarrenseite
a) MKS
b) FEM (MKS?)
c) KOS

Vgl. Dynamik I Skript, S. 2.2
b) FEM (MKS?)
c) KOS

Vgl. Dynamik I Skript, S. 2.2
Betrachtet wird das schwingende Einfreiheitsgradsystem in der allgemeinen Form:
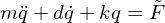
Benötigt man die Anfangsbedingungen der
der
Schwingung zur Aufstellung der folgenden Lösung:
- partikuläre Lösung
- homogene Lösung
- stationäre Lösung (d=0) (ohne Dämpfung)
- stationäre Lösung (d ≠0)
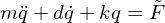
Benötigt man die Anfangsbedingungen
 der
derSchwingung zur Aufstellung der folgenden Lösung:
- partikuläre Lösung
- homogene Lösung
- stationäre Lösung (d=0) (ohne Dämpfung)
- stationäre Lösung (d ≠0)

1 Auszug: Wie schon zu Beginn des Abschnitts 4.2 erwähnt, wird bei vorhandener Dämpfung der homogene Lösungsanteil mit der Zeit bedeutungslos. (Je groser dabei D, desto schneller klingt der homogene Anteil ab, Gleichung (4.24).) Damit spielen gemäß Gleichung (4.24) auch die Anfangsbedingungen keine Rolle mehr. Die Langzeitantwort besteht somit nur noch aus der partikularen Lösung qp(t) allein.
Beschreiben Sie den Vorgang der photogrammetrischen Ermittlung von Dehnungen.

Bild 3.2.16 zeigt das prinzipielle Schema zur Dehnungsermittlung mit Hilfe zweier Kameras. Diese verfolgen die Bewegung eines Musters, das auf das interessierende Bauteil bzw. die Werkstoffprobe aufgebracht wurde und sich unter der Belastung des Prüflings verformt (Anstelle des Musters können auch markante Oberflächenpunkte benutzt werden, die sich aus der Werkstoffstruktur oder der Oberflächenbeschaffenheit des Bauteils ergeben.) Durch Vergleich entsprechender Punkte des ursprünglichen und des verzerrten Musters mit Mitteln der digitalen
Bildverarbeitung können überall auf der Oberfläche des Prüfobjekts die örtlichen Dehnungen ermittelt werden. Der Gebrauch zweier Kameras in Verbindung mit Stereoverfahren ermöglicht dabei die Betrachtung räumlicher Dehnungsbewegungen sowie die Untersuchung an gekrümmten Oberflächen.
(vgl. Versuchstechnik Skript, S. 3.18)
Kurzfassung: Verfolgung der Bewegung eines Musters auf einem Bauteil
Nennen Sie mind. zwei mögliche, wesentliche Störquellen bei der thermographischen Temperaturermittlung mit Infrarotkameras.
- Wärmestrahlung der Probe durch eine ungünstige Oberfläche (Reflektion von Wärmestrahlen)
- Örtlicher Emmissionsgrad der Probe
- Verschmutzung
- Raumtemperatur
(vgl. Versuchstechnik Skript, S. 3.18)
- Örtlicher Emmissionsgrad der Probe
- Verschmutzung
- Raumtemperatur
(vgl. Versuchstechnik Skript, S. 3.18)
Die Qualität von Messverstärkern wird üblicherweise anhand einer Reihe von Eigenschaften des Geräts beurteilt. Nennen Sie hierfür mind. zwei typische Kriterien.
- Linearität
- Nullpunktstabilität
- Amplitudenfrequenzgang
- Sprungantwort
- Signal-Rausch-Spannungsverhältniss
- Eingangs- und Ausgangswiederstand
(vgl. Versuchstechnik Skript, S. 3.22ff)
- Nullpunktstabilität
- Amplitudenfrequenzgang
- Sprungantwort
- Signal-Rausch-Spannungsverhältniss
- Eingangs- und Ausgangswiederstand
(vgl. Versuchstechnik Skript, S. 3.22ff)
Was besagt das Prinzip von St. Venant?
Aussage:
Statisch äquivalente Kraftsysteme haben in hinreichendem Abstand vom Krafteinleitungsbereich die gleiche Wirkung. Bei Vollkörpern ist dieser Abstand etwa so groß wie die Abmessungen des Krafteinleitungsbereiches. Bei dünnwandigen Trägern und Schalen kann dieser Abstand auch ein Mehrfaches des Krafteinleitungsbereiches betragen.
Alternative Formulierung des Prinzips von St. Venant:
Die Wirkung einer Gleichgewichtskraftgruppe (d.h. einer Kraftgruppe, deren Momentenfeld Null ist) verschwindet in hinreichendem Abstand vom Krafteinleitungsbereich.

Statisch äquivalente Kraftsysteme haben in hinreichendem Abstand vom Krafteinleitungsbereich die gleiche Wirkung. Bei Vollkörpern ist dieser Abstand etwa so groß wie die Abmessungen des Krafteinleitungsbereiches. Bei dünnwandigen Trägern und Schalen kann dieser Abstand auch ein Mehrfaches des Krafteinleitungsbereiches betragen.
Alternative Formulierung des Prinzips von St. Venant:
Die Wirkung einer Gleichgewichtskraftgruppe (d.h. einer Kraftgruppe, deren Momentenfeld Null ist) verschwindet in hinreichendem Abstand vom Krafteinleitungsbereich.

Ein Stabelement, welches einen quadratischen Verschiebungsausdruck erhalten soll, benötigt 3 Elementknoten, damit die Koeffizienten der normierten Ansatzfunktion eindeutig bestimmt werden können. Warum kommt der Bernoulli-Balken mit 2 Elementen aus?
quad. Ansatz => u=a+b*x+c*x^2
a,b,c sind die Freiwerte > 3 Freiwerte nötig > 3 Elementknoten nötig beim Stab Bernoulli Balken: 2 Freiwerte pro Knoten: Omega, Phi kubischer Ansatz => u=a+b*x+c*x^2+d*x^3
4 Freiwerte --> 2 Knoten nötig (da 2 EW pro Knoten)

a,b,c sind die Freiwerte > 3 Freiwerte nötig > 3 Elementknoten nötig beim Stab Bernoulli Balken: 2 Freiwerte pro Knoten: Omega, Phi kubischer Ansatz => u=a+b*x+c*x^2+d*x^3
4 Freiwerte --> 2 Knoten nötig (da 2 EW pro Knoten)

Erklären sie den Satz von Maxwell
Sonderfall vom Satz von Betti. Aussage:d_ik=d_ki, d.h. die Verschiebungsgröße an der Stell i zufolge der Lastgröße 1 an der STelle k ist gleich der Verschiebungsgröße an der Stelle k zufolge der Lastgröße, dabei sind die Last- und Verschiebungsgrößen in i bzw. k einander zugeordnet.
Beschreiben sie stichwortartig die Lösungsschritte bei der Strukturberechnung nach der Methode der Finite Elemente.
1) Elementsteifigkeitsmatrix aufstellen --> zur Gesamtsteifigkeitsmatrix zusammenbauen
2) Aufstellen der Lastspalte
3) Berücksichtigung der RB
4) Lösen des Gleichungsystems
5) Nachlaufrechnung zur Bestimmung von Längs-, Querkräften, Momenten und Spannungen
2) Aufstellen der Lastspalte
3) Berücksichtigung der RB
4) Lösen des Gleichungsystems
5) Nachlaufrechnung zur Bestimmung von Längs-, Querkräften, Momenten und Spannungen
Flashcard set info:
Author: carrera-911
Main topic: Bauingenieurwesen
Topic: ISD
Published: 19.03.2010
Card tags:
All cards (96)
no tags







 statische Randbedingungen (Statik)
statische Randbedingungen (Statik)



 .
. ,
,  und
und  .
.