diskret vs. stetiges Merkmal
| Diskretes Merkmal | Stetiges Merkmal |
| abzählbar viele Werte "voneinander getrennte Werte" | überabzählbar viele Werte, meist aus intervall |
| z.B. Anzahl der MA | z.B. Längenmaße, Geld |
Tags: #deskriptiv
Source:
Source:
Merkmalstypen
| Skalentyp | Nominal | Ordinal | Kardinal |
| Beschr. | Nur Unterscheidung gleich/ungleich | auch nach "Größe" ordnebar | Verhältnisse haben einen Sinn |
| Beispiel | Augenfarbe | Wohnort (PLZ) | Alter |
| Operat. | =,≠ | =,≠,<,> | =,≠,<,>,+,-,*,/ |
| Lageparamenter | Modus D (dichtester Wert) | Modus D, Median z (Zentralwert) | Modus D, Median z, arith. Mittel 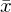 |
| Inform. Grad | gering | mittel | hoch |
| Empfindl. bei Messfehlern | gering | mittel | hoch |
Tags: #deskriptiv
Source:
Source:
Lageparamenter
Modus D: dichtester Wert (relativ häufigster Wert, Klassenbreite muss berücksichtigt werden)
Median z: Zentralwert ist derjenige Beobachtungswert bei dem mindestens 50% aller Beobachtungen kleiner oder gleich sind und mindestens 50% aller Beobachtungen größer oder gleich sind.
Abschätzen:

wenn ordinal und Werte unterschiedlich in der mitte, dann kein z bestimmbar
Berechnen
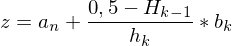
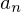 linke Grenze von betroffener Klasse
linke Grenze von betroffener Klasse
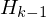 Kummulierte rel. Häufigkeit von vorhergehender Klasse
Kummulierte rel. Häufigkeit von vorhergehender Klasse
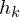 rel. Häufigkeit von betroffener Klasse
rel. Häufigkeit von betroffener Klasse
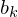 Klassenbreite von betroffener Klasse
Klassenbreite von betroffener Klasse
arithmetische Mittel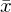 :
:

Median z: Zentralwert ist derjenige Beobachtungswert bei dem mindestens 50% aller Beobachtungen kleiner oder gleich sind und mindestens 50% aller Beobachtungen größer oder gleich sind.
Abschätzen:

wenn ordinal und Werte unterschiedlich in der mitte, dann kein z bestimmbar
Berechnen
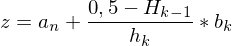
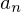 linke Grenze von betroffener Klasse
linke Grenze von betroffener Klasse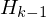 Kummulierte rel. Häufigkeit von vorhergehender Klasse
Kummulierte rel. Häufigkeit von vorhergehender Klasse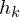 rel. Häufigkeit von betroffener Klasse
rel. Häufigkeit von betroffener Klasse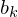 Klassenbreite von betroffener Klasse
Klassenbreite von betroffener Klassearithmetische Mittel
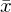 :
: 
Tags: #deskriptiv
Source:
Source:
Datengewinnung
Primäre Statistik: ursüungliche Erhebung von Daten zu statistischen Zwecken
z..B. Kundenbefragung
Sekundäre Statistik: bereits vorhandene Informationen, die für anderen Zweck gesammelt wurden, werden im nachhinein statistisch aufbereitet
z.B. Steuerstatistiken
z..B. Kundenbefragung
Sekundäre Statistik: bereits vorhandene Informationen, die für anderen Zweck gesammelt wurden, werden im nachhinein statistisch aufbereitet
z.B. Steuerstatistiken
Tags: #deskriptiv
Source:
Source:
Datenarten
Vorliegende Daten können von verschiedenen Arten sein:
Einzeldaten: viele noch nicht bearbeitete Daten, Urliste
Gruppierte Daten: gleiche Nennungen zusammengefasst
Klassierte Daten: ähnliche Nennungen zusammengefasst
Einzeldaten: viele noch nicht bearbeitete Daten, Urliste
Gruppierte Daten: gleiche Nennungen zusammengefasst
Klassierte Daten: ähnliche Nennungen zusammengefasst
Tags: #deskriptiv
Source:
Source:
Begriffe
Klassenmitte: 
Klassenbreite:
absolute Klassenhäufigkeit: Anzahl Einheiten die in k-te Klasse fallen
Häufigkeitsdichte: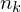 (absol. Häufigkeit)/
(absol. Häufigkeit)/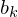 (Klassenbreite)
(Klassenbreite)
relative Klassenhäufigkeit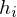 : Anteil
: Anteil 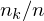
kumulierte relative Klassenhäufigkeit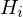 : rel. Häufigkeit der vorhergehenden Klassen + rel. Häufigkeit der aktuellen Klasse
: rel. Häufigkeit der vorhergehenden Klassen + rel. Häufigkeit der aktuellen Klasse
Spannweite (Range): Differenz zwischen kleinsten und größten Merkmalswert
Masse: Daten von 9 Personen
Merkmal: Bildungsstand
Mermalsausprägung: Gering (G)
Einheit: Mittleres Alter
Maßzahl: Alter 25 Jahre
Merkmalsträger: Person F

Klassenbreite:

absolute Klassenhäufigkeit: Anzahl Einheiten die in k-te Klasse fallen
Häufigkeitsdichte:
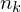 (absol. Häufigkeit)/
(absol. Häufigkeit)/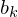 (Klassenbreite)
(Klassenbreite)relative Klassenhäufigkeit
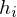 : Anteil
: Anteil 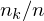
kumulierte relative Klassenhäufigkeit
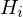 : rel. Häufigkeit der vorhergehenden Klassen + rel. Häufigkeit der aktuellen Klasse
: rel. Häufigkeit der vorhergehenden Klassen + rel. Häufigkeit der aktuellen KlasseSpannweite (Range): Differenz zwischen kleinsten und größten Merkmalswert
Masse: Daten von 9 Personen
Merkmal: Bildungsstand
Mermalsausprägung: Gering (G)
Einheit: Mittleres Alter
Maßzahl: Alter 25 Jahre
Merkmalsträger: Person F
Tags: #deskriptiv
Source:
Source:
geometrisches Mittel
z.B. Wachstumsraten wirken sich multiplikativ aus. Um durchschnittliche Wachstumsrate zu ermitteln benötigt man geom. Mittel:
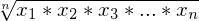
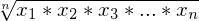
Tags: #deskriptiv
Source:
Source:
Histogramm
- stellt klassierte Daten über Rechtecke, die sich über die Klassenbreite spannen, dar.
- Höhe ergibt sich als Quotient der Klassenhäufigkeit und Klassenbreite (Dichte)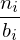
Nicht einfach die Häufigkeiten eintragen!

- Höhe ergibt sich als Quotient der Klassenhäufigkeit und Klassenbreite (Dichte)
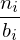
Nicht einfach die Häufigkeiten eintragen!

Tags: #deskriptiv
Source:
Source:
Box-Plot
Gibt Eindruck darüber , in welchem Bereich die Daten liegen und wie sie sich verteilen. Fünf-Punkte-Zusammenfassung: Median, zwei Quartile, beiden Extremwerte
1.Unterteilung in 4 Quartile:
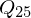
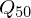 (gleich wie Zentralwert z)
(gleich wie Zentralwert z)
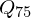
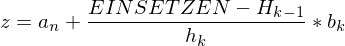
2. Spannbreite aller Werte horizontal darstellen (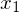 bis
bis 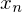
3.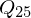 ,
, 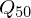 und
und 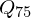 einzeichnen und folgendermaßen verbinden.
einzeichnen und folgendermaßen verbinden.
4.
1.Unterteilung in 4 Quartile:
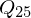
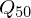 (gleich wie Zentralwert z)
(gleich wie Zentralwert z)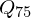
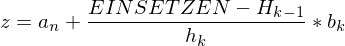
2. Spannbreite aller Werte horizontal darstellen (
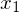 bis
bis 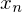
3.
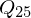 ,
, 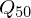 und
und 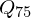 einzeichnen und folgendermaßen verbinden.
einzeichnen und folgendermaßen verbinden.4.

Tags: #deskriptiv
Source:
Source:
Varianz, Standardabweichung
Varianz: mittlere quadratische Abweichung vom arith. Mittelwert

Standardabweichung:"Streuung um den Mittelwert"
Wurzel aus Varianz


Standardabweichung:"Streuung um den Mittelwert"
Wurzel aus Varianz

Tags: #deskriptiv
Source:
Source:
Lorenzkurve 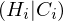
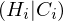
gibt an, welcher Anteil der Gesamtmerkalsbetrag vom welchem Anteil der Merkmalsträger getragen wird
1. Graphen zeichnen
2. Winkelhalbierende Einzeichnen ("faire Verteilung")
3. Punkte von Lorenzkurve eintragen
4. Punkte verbinden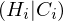
5. Kurve interpretieren
6. Gini Koeffizient bestimmen


1. Graphen zeichnen
2. Winkelhalbierende Einzeichnen ("faire Verteilung")
3. Punkte von Lorenzkurve eintragen
4. Punkte verbinden
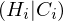
5. Kurve interpretieren
6. Gini Koeffizient bestimmen


Tags: #deskriptiv
Source:
Source:
Gini-Koeffizient
Def:
quantitatives Maß zur Messung des un/gleichheitsgrades (sog. Disparität) einer Verteilung
Umso höher der Gini-Koeffizient/bzw. die Fläche zwischen Winkelhalbierender und Lorenzkurve, desto ungleicher die Verteilung:
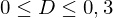 gering
gering
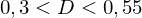 mittel
mittel
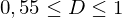 stark/hoch
stark/hoch

Formel:
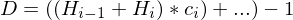
bzw. wenn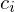 unbekannt:
unbekannt:

quantitatives Maß zur Messung des un/gleichheitsgrades (sog. Disparität) einer Verteilung
Umso höher der Gini-Koeffizient/bzw. die Fläche zwischen Winkelhalbierender und Lorenzkurve, desto ungleicher die Verteilung:
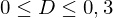 gering
gering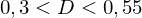 mittel
mittel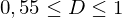 stark/hoch
stark/hoch
Formel:
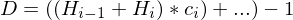
bzw. wenn
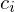 unbekannt:
unbekannt:
Tags: #deskriptiv
Source:
Source:
Konzetrationsanteil 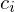
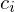
je nach Verteilungstyp verschiedene Formeln:

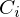 kummulierter Konzetrationsanteil
kummulierter Konzetrationsanteil
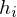 Anteil an den Nennungen (
Anteil an den Nennungen (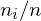 )
)
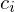 Anteil der
Anteil der 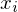 -Werte an allen X Werten
-Werte an allen X Werten

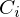 kummulierter Konzetrationsanteil
kummulierter Konzetrationsanteil 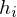 Anteil an den Nennungen (
Anteil an den Nennungen (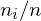 )
)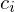 Anteil der
Anteil der 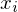 -Werte an allen X Werten
-Werte an allen X WertenTags: #deskriptiv
Source:
Source:
Zweidimensionale Datensätze
Werden bei n Merkmalsträgern einer statistischen Masse zwei Merkmale X und Y erfasst, so erhält man einen bivarianten Datensatz
--> Zweidimensionale Häufigkeitstabelle

Randverteilung: Zeilen bzw. Spaltensumme
i = Zeilennummer
j = Spaltennummer
--> Zweidimensionale Häufigkeitstabelle

Randverteilung: Zeilen bzw. Spaltensumme
i = Zeilennummer
j = Spaltennummer
Tags: #zweidim
Source:
Source:
Statistische Unabhängigkeit
X und Y sind dann statistisch unabhängig, wenn für alle möglichen Werte von j und i gilt:
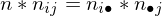
weiterer Hinweis auf stat. Unabhängigkeit: Kovarianz
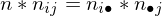
weiterer Hinweis auf stat. Unabhängigkeit: Kovarianz
Tags: #zweidim
Source:
Source:
Kovarianz
ist Ausdruckdes Zusammenhangs zwischen zwei metrisch skalierten Variablen.
gibt Hinweis auf stat. Unabhängigkeit

Wenn X und Y stat. unabhängig sind, dann muss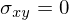
Wenn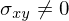 dann sind X und Y nicht stat. unabhängig
dann sind X und Y nicht stat. unabhängig
gibt Hinweis auf stat. Unabhängigkeit

Wenn X und Y stat. unabhängig sind, dann muss
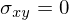
Wenn
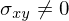 dann sind X und Y nicht stat. unabhängig
dann sind X und Y nicht stat. unabhängigTags: #zweidim
Source:
Source:
Regressionsgerade
Ziel: Repräsentant (Funktion) für die Punktwolke des zweidim. Datensatzes finden.
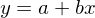

Dabei geht die Funktion durch den Schwerpunkt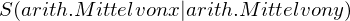
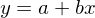

Dabei geht die Funktion durch den Schwerpunkt
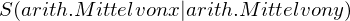
Tags: #zweidim
Source:
Source:
Korrelationskoeffizient nach Bravis-Person

Daraus ergibt sich Bestimmtheitsmaß B folgendermaßen:
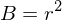
Interpretation von B:
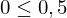 geringe Korelation
geringe Korelation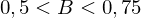 mittlere Korelation
mittlere Korelation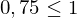 starke Korelation
starke Korelation--> beurteilt damit auch, wie geeignet die Regressionsgerade als Repräsentant ist
Tags: #zweidim
Source:
Source:
Verhältnis- und Indexzahlen
1. Gliederungszahlen
haben keine Dimension
2. Beziehungszahlen
haben Einheiten und schaffen Verbindung
3. Messzahlen
Entwicklung, Veränderung: Bei Messzahlen enthalten Zähler und Nenner gleichartige Mengen, die sich aber auf unterschiedliche Zeitpunkte
4. Preisindizes:
Preisindizes haben die Aufgabe, die Preisentwicklung der Gesamtheit von Gütern zwischen Basis-(0) und Berichtsjahr (t) abzubilden. Es gelten folgende Größen:

haben keine Dimension
2. Beziehungszahlen
haben Einheiten und schaffen Verbindung
3. Messzahlen
Entwicklung, Veränderung: Bei Messzahlen enthalten Zähler und Nenner gleichartige Mengen, die sich aber auf unterschiedliche Zeitpunkte
4. Preisindizes:
Preisindizes haben die Aufgabe, die Preisentwicklung der Gesamtheit von Gütern zwischen Basis-(0) und Berichtsjahr (t) abzubilden. Es gelten folgende Größen:

Tags: #index
Source:
Source:
Preisindex
Preis variabel, Menge konstant: Aussagen über die durchschnittliche Preisänderung
Laspeyres:

Paasche:

Fischer:

Laspeyres:

Paasche:

Fischer:

Tags: #index
Source:
Source:
Mengenindex
Preis konstant, Menge variabel: Aussagen über die durchschnittliche Mengenänderung
Laspeyres:

Paasche:

Fischer:

Laspeyres:

Paasche:

Fischer:

Tags: #index
Source:
Source:
Indexreihen Umbasierung
Indexreihen mit unterschiedlicher Basisperiode werden auf eine Basisperiode bezogen:

Index 2 wird mit /108,3 dividiert --> umbasierter Index 2
Wie komme ich von Index 1 zu Index 2?

Index 2 wird mit /108,3 dividiert --> umbasierter Index 2
Wie komme ich von Index 1 zu Index 2?
Tags: #index
Source:
Source:
Indexreihen Verknüpfung
1. mit Überlappung
Überlappungsstelle als Faktor verwenden und fehlende Zahlen ergänzen
2. ohne Überlappung
-> es muss geschätzt (lin. Regression) werden, um Überlappung herzustellen
1. Jahre (X) durch einfachere Zahlen ersetzen
2. mithilfe von lin. Regression Funktion bestimmen
3. Überlappungsstelle(n) ausrechnen
4. mit dadurch erhaltenem Faktor die fehlenden Stellen berechnen
Überlappungsstelle als Faktor verwenden und fehlende Zahlen ergänzen
2. ohne Überlappung
-> es muss geschätzt (lin. Regression) werden, um Überlappung herzustellen
1. Jahre (X) durch einfachere Zahlen ersetzen
2. mithilfe von lin. Regression Funktion bestimmen
3. Überlappungsstelle(n) ausrechnen
4. mit dadurch erhaltenem Faktor die fehlenden Stellen berechnen
Tags: #index
Source:
Source:
Wahrscheinlichkeitsrechnung
Begriffe:
Zufallsexperiment: wiederholter Vorgang, dessen Ergebnis vom Zufall abhäng
Elementarereignisse: Ergebnisse (Realisation) des Zufallsexperiment
Ereignisraum G: Mege der Elementarereignisse
Ereignis A: Teilmenge von G
Laplace Experiment: Zufallsexperiment mit nur 2 Elementarereignissen
Zufallsexperiment: wiederholter Vorgang, dessen Ergebnis vom Zufall abhäng
Elementarereignisse: Ergebnisse (Realisation) des Zufallsexperiment
Ereignisraum G: Mege der Elementarereignisse
Ereignis A: Teilmenge von G
Laplace Experiment: Zufallsexperiment mit nur 2 Elementarereignissen
Verknüpfung von Ereignissen
Vereinigung zweier Ereignisse A, B:
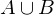 ist die Menge aller Elementarereignisse, die entweder zu A oder zu B oder zu A und B gemeinsam gehören.
ist die Menge aller Elementarereignisse, die entweder zu A oder zu B oder zu A und B gemeinsam gehören.
Durchschnitt zweier Ereignisse A, B:
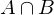 ist die Menge aller Elementarereignisse, die sowohl zu A als auch zu B gehören.
ist die Menge aller Elementarereignisse, die sowohl zu A als auch zu B gehören.
Additionssatz:
Wie hoch ist die Wahrscheinlichkeit, dass bei beliebigen, sich nicht ausschließenden Ereignissen A, B eines Zufallsexperiments, A oder B eintritt?
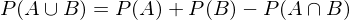
Bedingte Wahrscheinlichkeit, Multiplikationssatz, Pfadregel:
Das Eintreten von Ereignissen in Abhängigkeit von bestimmten anderen Ereignissen. Wir lesen: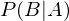 ist die Wahrscheinlichkeit, dass B eintritt, wenn A eingetreten ist.
ist die Wahrscheinlichkeit, dass B eintritt, wenn A eingetreten ist.

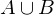 ist die Menge aller Elementarereignisse, die entweder zu A oder zu B oder zu A und B gemeinsam gehören.
ist die Menge aller Elementarereignisse, die entweder zu A oder zu B oder zu A und B gemeinsam gehören.Durchschnitt zweier Ereignisse A, B:
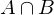 ist die Menge aller Elementarereignisse, die sowohl zu A als auch zu B gehören.
ist die Menge aller Elementarereignisse, die sowohl zu A als auch zu B gehören.Additionssatz:
Wie hoch ist die Wahrscheinlichkeit, dass bei beliebigen, sich nicht ausschließenden Ereignissen A, B eines Zufallsexperiments, A oder B eintritt?
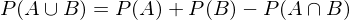
Bedingte Wahrscheinlichkeit, Multiplikationssatz, Pfadregel:
Das Eintreten von Ereignissen in Abhängigkeit von bestimmten anderen Ereignissen. Wir lesen:
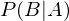 ist die Wahrscheinlichkeit, dass B eintritt, wenn A eingetreten ist.
ist die Wahrscheinlichkeit, dass B eintritt, wenn A eingetreten ist.
Zerlegung von Wahrscheinlichkeiten
Wahrscheinlichkeiten können Teilmengen von anderen Wahrscheinlichkeiten darstellen.
Beispiel: 3 verschiedene Arten Apfelsaft in Regal.
A: 30%
B: 50%
C: 20%
Verfallsdatum überschritten:
A. 4%
B: 3%
C: 6%
s=Verfallsdatum überschritten
P(s) = Teilmengen der einzelnen Fehlerraten
Beispiel: 3 verschiedene Arten Apfelsaft in Regal.
A: 30%
B: 50%
C: 20%
Verfallsdatum überschritten:
A. 4%
B: 3%
C: 6%
s=Verfallsdatum überschritten
P(s) = Teilmengen der einzelnen Fehlerraten
Eindim. Zufallsvariablen und ihre Verteilung
Diskrete Zufallsvariablen:
Wahrscheinlichkeiten lassen sich mithilfe von Wahrscheinlichkeitsfunktion berechnen.
Verteilunsfunktion gibt die Wahrscheinlichkeit an, dass die Zufallsvariable X höchsten den Wert xj annimmt:

Stetige Zufallsvariablen:
Wahrscheinlichkeiten werden nur für Intervalle angegeben. Wahrscheinlichkeitsdichte (Dichtefunktion)
Verteilungsfunktion gibt Wahrscheinlichkeit an, dass X höchstens den Wert x annimmt.

Wahrscheinlichkeiten lassen sich mithilfe von Wahrscheinlichkeitsfunktion berechnen.
Verteilunsfunktion gibt die Wahrscheinlichkeit an, dass die Zufallsvariable X höchsten den Wert xj annimmt:

Stetige Zufallsvariablen:
Wahrscheinlichkeiten werden nur für Intervalle angegeben. Wahrscheinlichkeitsdichte (Dichtefunktion)
Verteilungsfunktion gibt Wahrscheinlichkeit an, dass X höchstens den Wert x annimmt.







 oder
oder
 oder
oder

