Zerfällungskörper
Sei  . Eine endliche Erweiterung
. Eine endliche Erweiterung  heißt ein Zerfällungskörper von
heißt ein Zerfällungskörper von  , falls
, falls  über
über 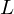 in Linearfaktoren zerfällt, etwa
in Linearfaktoren zerfällt, etwa 
 . Eine endliche Erweiterung
. Eine endliche Erweiterung  heißt ein Zerfällungskörper von
heißt ein Zerfällungskörper von  , falls
, falls  über
über 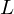 in Linearfaktoren zerfällt, etwa
in Linearfaktoren zerfällt, etwa 
Wurzelkörper
Ist  irreduzibel und ist
irreduzibel und ist  eine Erweiterung, für die ein
eine Erweiterung, für die ein 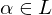 mit
mit  und
und  existiert, so heißt
existiert, so heißt 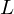 ein Wurzelkörper.
ein Wurzelkörper.
Gesehen: ist ein Wurzelkörper.
ist ein Wurzelkörper.
Eine Erweiterung heißt ein Wurzelkörper von
heißt ein Wurzelkörper von  über
über  , falls
, falls  mit
mit  und
und
 irreduzibel und ist
irreduzibel und ist  eine Erweiterung, für die ein
eine Erweiterung, für die ein 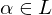 mit
mit  und
und  existiert, so heißt
existiert, so heißt 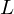 ein Wurzelkörper.
ein Wurzelkörper.Gesehen:
 ist ein Wurzelkörper.
ist ein Wurzelkörper.Eine Erweiterung
 heißt ein Wurzelkörper von
heißt ein Wurzelkörper von  über
über  , falls
, falls  mit
mit  und
und Körpererweiterung
Sei 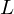 Körper und
Körper und  ein Teilkörper.
ein Teilkörper.
Man schreibt oft oder
oder  "
"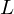 über
über  " und nennt
" und nennt  ein Körpererweiterung.
ein Körpererweiterung.
Man betrachte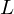 als
als  -VR. Die Dimension entspricht dem Grad
-VR. Die Dimension entspricht dem Grad 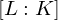 der Körpererweiterung.
der Körpererweiterung.
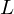 Körper und
Körper und  ein Teilkörper.
ein Teilkörper.Man schreibt oft
 oder
oder  "
"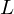 über
über  " und nennt
" und nennt  ein Körpererweiterung.
ein Körpererweiterung.Man betrachte
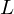 als
als  -VR. Die Dimension entspricht dem Grad
-VR. Die Dimension entspricht dem Grad 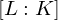 der Körpererweiterung.
der Körpererweiterung.Endliche Körpererweiterung
Die Körpererweiterung heißt endlich, falls ihr Grad endlich ist.
Ein nichttrivialer kommutativer Ring 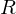 mit
mit 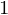 enthält als einzige Ideale
enthält als einzige Ideale  und
und 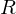 gdw...
gdw...
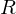 mit
mit 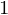 enthält als einzige Ideale
enthält als einzige Ideale  und
und 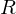 gdw...
gdw...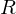 ein Körper ist.
ein Körper ist.Kreisteilungspolynom
Man setzt  . Es heißt das
. Es heißt das  -te Kreisteilungspolynom.
-te Kreisteilungspolynom.
Ist eine Primzahl, so ist
eine Primzahl, so ist  ein Eisensteinpolynom, also irreduzibel.
ein Eisensteinpolynom, also irreduzibel.
 . Es heißt das
. Es heißt das  -te Kreisteilungspolynom.
-te Kreisteilungspolynom.Ist
 eine Primzahl, so ist
eine Primzahl, so ist  ein Eisensteinpolynom, also irreduzibel.
ein Eisensteinpolynom, also irreduzibel.Was ist 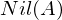 und wovon ist sie der Durchschnitt?
und wovon ist sie der Durchschnitt?
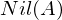 und wovon ist sie der Durchschnitt?
und wovon ist sie der Durchschnitt?Die Menge  ist genau der Durchschnitt aller Primideale.
ist genau der Durchschnitt aller Primideale.
Insbesondere ist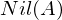 ein Ideal in
ein Ideal in  .
.
Korollar 3.11
 ist genau der Durchschnitt aller Primideale.
ist genau der Durchschnitt aller Primideale.Insbesondere ist
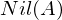 ein Ideal in
ein Ideal in  .
.Korollar 3.11
Einheitswurzel
 Ring und
Ring und  natürliche Zahl mit
natürliche Zahl mit 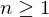 . Ein
. Ein 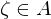 heißt
heißt  -te Einheitswurzel, falls eine der folgenden äquivalten Bedingungen erfüllt sind:
-te Einheitswurzel, falls eine der folgenden äquivalten Bedingungen erfüllt sind:(a)
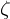 ist Nullstelle des Polynoms
ist Nullstelle des Polynoms 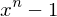
(b) Es ist
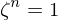
- ist
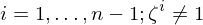 , so heißt
, so heißt 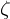 primitiv.
primitiv.-
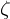 ist Element der Einheitengruppe, insbesondere bilden alle
ist Element der Einheitengruppe, insbesondere bilden alle  -ten Einheitswurzeln eine Untergruppe der Einheitengruppe.
-ten Einheitswurzeln eine Untergruppe der Einheitengruppe.Körperweiterung
Sei 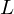 ein Körper mit
ein Körper mit  einem Teilkörper von
einem Teilkörper von 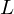 , so nennt man
, so nennt man  eine Körpererweiterung.
eine Körpererweiterung.
 heißt der Grad der Erweiterung.
heißt der Grad der Erweiterung.
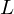 ein Körper mit
ein Körper mit  einem Teilkörper von
einem Teilkörper von 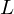 , so nennt man
, so nennt man  eine Körpererweiterung.
eine Körpererweiterung. heißt der Grad der Erweiterung.
heißt der Grad der Erweiterung.Der Grad einer Erweiterung mit Zwischenkörper ist multiplikativ, das heißt:
Ist  so ist der Grad
so ist der Grad 
 so ist der Grad
so ist der Grad 
 -Homomorphismus (Definition)
-Homomorphismus (Definition)Für zwei Körpererweiterungen 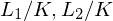 ist eine Abbildung (Ringhomomorphismus)
ist eine Abbildung (Ringhomomorphismus)  ein
ein  -Homomorphismus.
-Homomorphismus.
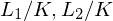 ist eine Abbildung (Ringhomomorphismus)
ist eine Abbildung (Ringhomomorphismus)  ein
ein  -Homomorphismus.
-Homomorphismus.Kriterium von der Teilbarkeit der Konstanten und des Leitkoeffizienten
Sei  und
und 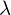 eine Nullstelle in
eine Nullstelle in  (
( ). Dann ist
). Dann ist  mit
mit 
 und
und 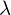 eine Nullstelle in
eine Nullstelle in  (
( ). Dann ist
). Dann ist  mit
mit 
Eisensteinkriterium
 faktoriell,
faktoriell,  .
.  . Gibt es ein
. Gibt es ein  prim in
prim in  mit
mit  teilt nicht
teilt nicht  ,
,  teilt
teilt  und
und  teilt nicht
teilt nicht  , dan ist
, dan ist  irreduzibel in
irreduzibel in 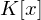 .
.Eisensteinkriterium (Satz 5.12)
 faktoriell,
faktoriell,  . Sei
. Sei  . Gibt es ein Primelement
. Gibt es ein Primelement  von
von  mit
mit  für
für  und
und  , so ist
, so ist  irreduzibel in
irreduzibel in 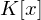 .
.Angenommen mithilfe von Korollar 5.6 finden sich keine Nullstellen von  über
über 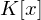 , ist
, ist  dann irreduzibel über
dann irreduzibel über 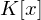 ?
?
 über
über 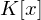 , ist
, ist  dann irreduzibel über
dann irreduzibel über 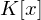 ?
?Nein, das folgt nicht unbedingt.
Es hilft nur zu erfahren, ob es reduzibel ist.
Es hilft nur zu erfahren, ob es reduzibel ist.
Wann sind Ideale Maximal?
Ein Ideal  in
in  ist maximal, wenn erstens gilt, dass für alle Ideale
ist maximal, wenn erstens gilt, dass für alle Ideale 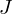 mit
mit  entweder
entweder  oder
oder  gilt.
gilt.
Zweitens, wenn der Faktorring ein Körper ist.
ein Körper ist.
 in
in  ist maximal, wenn erstens gilt, dass für alle Ideale
ist maximal, wenn erstens gilt, dass für alle Ideale 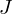 mit
mit  entweder
entweder  oder
oder  gilt.
gilt.Zweitens, wenn der Faktorring
 ein Körper ist.
ein Körper ist.Wann gilt, dass  mit
mit 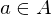 maximal, so ist
maximal, so ist  irreduzibel?
irreduzibel?
 mit
mit 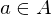 maximal, so ist
maximal, so ist  irreduzibel?
irreduzibel?Die Voraussetzung  ist integere und
ist integere und  reicht schon aus.
reicht schon aus.
 ist integere und
ist integere und  reicht schon aus.
reicht schon aus.Wann gilt  mit
mit 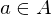 maximal, gdw.
maximal, gdw.  irreduzibel.
irreduzibel.
 mit
mit 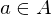 maximal, gdw.
maximal, gdw.  irreduzibel.
irreduzibel.Dazu muss  ein nullteilerfreier Hauptidealring sein.
ein nullteilerfreier Hauptidealring sein.
Beweis:
 ein nullteilerfreier Hauptidealring sein.
ein nullteilerfreier Hauptidealring sein.Beweis:
Definition von Inhalt eines Polynoms
 faktorieller Ring,
faktorieller Ring,  .
.Für ein Polynom
 gilt,
gilt, 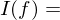 der
der 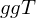 aller Koeffizienten von
aller Koeffizienten von  (Der
(Der 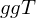 ist damit aus
ist damit aus 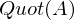 ).
).Was ist ein primitives Polynom?
Ein Polynom  heißt primitiv, wenn der Inhalt
heißt primitiv, wenn der Inhalt  assoziiert zu
assoziiert zu 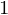 ist, also
ist, also  .
.
Bedeutet: Die Koeffizienten in dem Polynom sind Teilerfremd.
 heißt primitiv, wenn der Inhalt
heißt primitiv, wenn der Inhalt  assoziiert zu
assoziiert zu 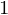 ist, also
ist, also  .
.Bedeutet: Die Koeffizienten in dem Polynom sind Teilerfremd.
Was gilt in Polyomringen über Körpern in Bezug auf die Primitivität der Elemente?
Ist  Körper, so ist jedes Polynom
Körper, so ist jedes Polynom  primitiv.
primitiv.
 Körper, so ist jedes Polynom
Körper, so ist jedes Polynom  primitiv.
primitiv.Welcher Ringtyp liegt dem Lemma von Gauß zugrunde?
Für das Lemma von Gauß wird  faktoriell und
faktoriell und  betrachtet.
betrachtet.
 faktoriell und
faktoriell und  betrachtet.
betrachtet.Jedes Ideal 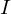 in
in  ist unter
ist unter 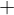 und
und  abgeschlossen, aber...
abgeschlossen, aber...
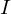 in
in  ist unter
ist unter 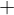 und
und  abgeschlossen, aber...
abgeschlossen, aber...... ist nur dann ein Teilring von  , wenn
, wenn  ist.
ist.
 , wenn
, wenn  ist.
ist.Für jeden Ringhomo  ist der Kern...
ist der Kern...
 ist der Kern...
ist der Kern......ein Ideal in  .
.
Beweis: Seien und
und  . Also
. Also  . Mit
. Mit 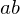 ist
ist  , also
, also  .
.
Additivität klar.
 .
.Beweis: Seien
 und
und  . Also
. Also  . Mit
. Mit 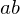 ist
ist  , also
, also  .
.Additivität klar.
Hauptidealring
 heißt Hauptidealring, falls
heißt Hauptidealring, falls  integer und jedes Ideal in
integer und jedes Ideal in  ein maximales Ideal ist.
ein maximales Ideal ist.In was lassen sich Elemente eines Hauptidealringes eindeutig zerlegen?
In irreduzible Elemente. Theorem 2.11, Beweis auf seleber Seite im Skript BII.
Faktorieller Ring
Ein Ring  heißt faktoriell, wenn
heißt faktoriell, wenn  integer ist und die äquivalenten Eigenschaften aus Theorem 4.5 besitzt, also:
integer ist und die äquivalenten Eigenschaften aus Theorem 4.5 besitzt, also:
(i) Jede Nicht-Einheit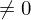 in
in  ist ein (endliches) Produkt von Primelementen
ist ein (endliches) Produkt von Primelementen
(ii) Jede Nicht-Einheit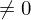 in
in  ist ein (endliches) Produkt aus irreduziblem Elementen und diese Darstellung ist Eindeutig bis auf Reihenfolge und Assoziertheit.
ist ein (endliches) Produkt aus irreduziblem Elementen und diese Darstellung ist Eindeutig bis auf Reihenfolge und Assoziertheit.
(iii) Es gibt keine unendlichen Teilerketten in und je zwei Elemente
und je zwei Elemente 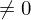 in
in  besitzen einen
besitzen einen 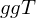 .
.
(iv) Es gibt keine unendlichen Teilerketten in und jedes irreduzible Element ist prim.
und jedes irreduzible Element ist prim.
 heißt faktoriell, wenn
heißt faktoriell, wenn  integer ist und die äquivalenten Eigenschaften aus Theorem 4.5 besitzt, also:
integer ist und die äquivalenten Eigenschaften aus Theorem 4.5 besitzt, also:(i) Jede Nicht-Einheit
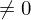 in
in  ist ein (endliches) Produkt von Primelementen
ist ein (endliches) Produkt von Primelementen(ii) Jede Nicht-Einheit
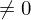 in
in  ist ein (endliches) Produkt aus irreduziblem Elementen und diese Darstellung ist Eindeutig bis auf Reihenfolge und Assoziertheit.
ist ein (endliches) Produkt aus irreduziblem Elementen und diese Darstellung ist Eindeutig bis auf Reihenfolge und Assoziertheit.(iii) Es gibt keine unendlichen Teilerketten in
 und je zwei Elemente
und je zwei Elemente 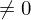 in
in  besitzen einen
besitzen einen 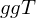 .
.(iv) Es gibt keine unendlichen Teilerketten in
 und jedes irreduzible Element ist prim.
und jedes irreduzible Element ist prim.Zentrum
Das Zentrum einer Gruppe 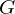 i.Z.
i.Z.  ist die Menge aller derjenigen
ist die Menge aller derjenigen  für die gilt:
für die gilt: 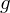 verknüpft mit
verknüpft mit  ist gleich
ist gleich  verknüpft mit
verknüpft mit 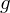 für alle
für alle  , also
, also  .
.
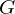 i.Z.
i.Z.  ist die Menge aller derjenigen
ist die Menge aller derjenigen  für die gilt:
für die gilt: 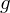 verknüpft mit
verknüpft mit  ist gleich
ist gleich  verknüpft mit
verknüpft mit 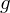 für alle
für alle  , also
, also  .
.Nilpotent
Ein nilpotentes Element 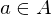 Ring ist ein Element, für das es ein
Ring ist ein Element, für das es ein 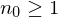 gibt, so dass für alle
gibt, so dass für alle  gilt
gilt  .
.
Man nennt den Nilpotenzindex.
den Nilpotenzindex.
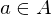 Ring ist ein Element, für das es ein
Ring ist ein Element, für das es ein 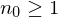 gibt, so dass für alle
gibt, so dass für alle  gilt
gilt  .
.Man nennt
 den Nilpotenzindex.
den Nilpotenzindex.Kette
Sei  Menge, sei
Menge, sei  .
.
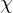 heißt eine Kette, falls für je zwei Elemente aus
heißt eine Kette, falls für je zwei Elemente aus 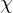 , dass das eine Element Teilmenge des anderen oder umgekehrt ist.
, dass das eine Element Teilmenge des anderen oder umgekehrt ist.
Also: Falls
 Menge, sei
Menge, sei  .
.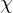 heißt eine Kette, falls für je zwei Elemente aus
heißt eine Kette, falls für je zwei Elemente aus 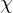 , dass das eine Element Teilmenge des anderen oder umgekehrt ist.
, dass das eine Element Teilmenge des anderen oder umgekehrt ist.Also: Falls

Was impliziert der Ringhomomorphismus 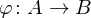 mit den Spektren
mit den Spektren  ?
?
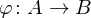 mit den Spektren
mit den Spektren  ?
?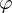 impliziert einen Homomorphismus
impliziert einen Homomorphismus  in Gegenrichtung mit
in Gegenrichtung mit  wobei
wobei  .
. Primideal
Ein Ideal 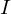 in
in  heißt prim, falls
heißt prim, falls  integer ist.
integer ist.
Genau dann ist also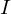 prim, wenn
prim, wenn  und
und 
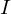 in
in  heißt prim, falls
heißt prim, falls  integer ist.
integer ist.Genau dann ist also
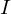 prim, wenn
prim, wenn  und
und 
Prim
Ein Element  heißt prim, falls das von ihm erzeugte Hauptideal
heißt prim, falls das von ihm erzeugte Hauptideal  ein Primideal ist.
ein Primideal ist.
 ist also genau dann prim, wenn
ist also genau dann prim, wenn 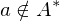 ist und für alle
ist und für alle  mit
mit  gilt:
gilt:  .
.
 heißt prim, falls das von ihm erzeugte Hauptideal
heißt prim, falls das von ihm erzeugte Hauptideal  ein Primideal ist.
ein Primideal ist. ist also genau dann prim, wenn
ist also genau dann prim, wenn 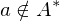 ist und für alle
ist und für alle  mit
mit  gilt:
gilt:  .
.Jedes maximale Ideal von  ist...
ist...
 ist...
ist...... ein Primideal.
Beweis: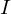 ein maximales Ideal in
ein maximales Ideal in  ist Körper
ist Körper  ist integer
ist integer  ist prim nach Definition.
ist prim nach Definition.
Beweis:
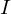 ein maximales Ideal in
ein maximales Ideal in  ist Körper
ist Körper  ist integer
ist integer  ist prim nach Definition.
ist prim nach Definition.Satz von Ruffini
Ist 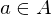 eine Nullstelle von
eine Nullstelle von  , so
, so  mit
mit  .
.
Beweis: (Leitkoeffizient ist Einheit in
(Leitkoeffizient ist Einheit in  ) also Polynomdivision möglich. Dividiere
) also Polynomdivision möglich. Dividiere  durch durhc
durch durhc  und erhalte Darstellung
und erhalte Darstellung  . Einsetzen von
. Einsetzen von  in
in  gibt mit
gibt mit  ein Nullstelle von
ein Nullstelle von  ,
, 
Also
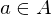 eine Nullstelle von
eine Nullstelle von  , so
, so  mit
mit  .
.Beweis:
 (Leitkoeffizient ist Einheit in
(Leitkoeffizient ist Einheit in  ) also Polynomdivision möglich. Dividiere
) also Polynomdivision möglich. Dividiere  durch durhc
durch durhc  und erhalte Darstellung
und erhalte Darstellung  . Einsetzen von
. Einsetzen von  in
in  gibt mit
gibt mit  ein Nullstelle von
ein Nullstelle von  ,
, 
Also

Satz von der Polynomdivision mit Rest über Ringen
 Ring.
Ring.  . Ist der Leitkoeffizient von
. Ist der Leitkoeffizient von 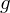 eine Einheit in
eine Einheit in  , so gibt es
, so gibt es  mit
mit  und
und  .
. Ring. Ist
Ring. Ist  und
und 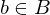 , so gibt es...
, so gibt es......genau einen Ringhomomorphismus  und mit
und mit  und
und  .
.
(Satz 1.4)
 und mit
und mit  und
und  .
.(Satz 1.4)
Zariski-spektrum
Die Menge aller Primideal von  heißt das (Zariski-)Spektrum von
heißt das (Zariski-)Spektrum von  ,in Zeichen
,in Zeichen  .
.
 heißt das (Zariski-)Spektrum von
heißt das (Zariski-)Spektrum von  ,in Zeichen
,in Zeichen  .
.Je zwei Elemente in  haben einen
haben einen 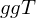 , bedeutet...
, bedeutet...
 haben einen
haben einen 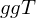 , bedeutet...
, bedeutet...... es gibt keine unendlichen Teilerketten in  .
.
 .
.Homomorphieatz (Ringe)
Sind  Ringe und
Ringe und  der Ringhomomorphismus von
der Ringhomomorphismus von  nach
nach  .
.
Dann ist ein Ideal in
ein Ideal in 
und ist isomorph zu
ist isomorph zu 
Klar, falls surjektiv, ist
surjektiv, ist  also
also  ist isomorph zu
ist isomorph zu 
 Ringe und
Ringe und  der Ringhomomorphismus von
der Ringhomomorphismus von  nach
nach  .
.Dann ist
 ein Ideal in
ein Ideal in 
und
 ist isomorph zu
ist isomorph zu 
Klar, falls
 surjektiv, ist
surjektiv, ist  also
also  ist isomorph zu
ist isomorph zu 
Stabilisator
Zu einer 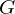 Operation heißt
Operation heißt 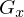 der Stabilisator.
der Stabilisator.
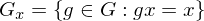
Zusammenhang mit Bahn: Es existiert Bijektion zwischen und
und  mit
mit  . Ist wohldefiniert.
. Ist wohldefiniert.
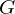 Operation heißt
Operation heißt 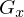 der Stabilisator.
der Stabilisator.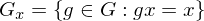
Zusammenhang mit Bahn: Es existiert Bijektion zwischen
 und
und  mit
mit  . Ist wohldefiniert.
. Ist wohldefiniert. Kern (Gruppenoperationen)
Der Kern einer Gruppenoperation 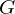 auf
auf  ist definiert als
ist definiert als  . Falls der Kern nur die Einheit enthält, heißt die Operation treu.
. Falls der Kern nur die Einheit enthält, heißt die Operation treu.
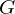 auf
auf  ist definiert als
ist definiert als  . Falls der Kern nur die Einheit enthält, heißt die Operation treu.
. Falls der Kern nur die Einheit enthält, heißt die Operation treu.Kartensatzinfo:
Autor: attila.rufius
Oberthema: Mathematik
Thema: Algebra
Veröffentlicht: 01.03.2010
Schlagwörter Karten:
Alle Karten (65)
keine Schlagwörter





 falls
falls  maximal, dann
maximal, dann gilt
gilt  .
. primitiv, so auch
primitiv, so auch 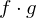 .
. .
.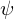 Ringhomomorphismen,
Ringhomomorphismen,  ist...
ist... nämlich
nämlich (für alle
(für alle  )
)  -mal.
-mal. 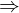
 ist die Norm eine Abbildung
ist die Norm eine Abbildung

 mit
mit 
 oder
oder  .
.
 und
und  .
. ,
,
