Welche Forderungen sind an das "objektive Messen" in den Sozialwissenschaften zu stellen?
- Testunabhängige Fähigkeitsmaße (Personenparameter) Die Messwerte (Fähigkeitsgrade) sollten nicht von dem Test (zufällig) verwendeten Items abhängen; denn eine Aussage über den Vergleich zweier Personen sollte unabhängig davon sein, welcher und wie viele Items dafür verwendet wurden, und zudem unabhängig davon, welche Person sonst noch getestet wurde.
- Stichprobenunabhängige Itemschwierigkeitsmaße (Itemparameter) Die Schwierigkeit von Testaufgaben sollte unabhängig von konkreten Stichproben (mit bestimmten Fähigkeitsverteilungen) quantifiziert werden können; Eine Aussage über den Vergleich zweier Items sollte unabhängig davon sein, welche und wie viele Personen dafür verwendet wurden, und welche Items sonst noch vorgelegt wurden.(Beispiel: Ein leichteres Item A und ein schwieriges Item B sollen diese Rangfolge [A kleiner als B] auch in anderen - etwas weniger begabten - Stichproben aufweisen.)
Die beiden Punkte entsprechen der Forderung von G. Rasch nach spezifischer Objektivität von Vergleichen und beinhaltet das Prinzip der sogenannten Stichprobenunabhängigkeit.
Tags: Item Response Theorie, Objektivität, Rasch-Modell
Quelle: S43
Quelle: S43
Was sind die Grundannahmen des Rasch-Modells als Skalenkonstruktionsmethode?
- Das RM geht nicht vom Rohwert (Testwert, Score) aus, sondern setzt beim einzelnen Item an. Damit wird eine Prüfung, ob alle Items dieselbe latente Dimension messen überhaupt erst möglich. Jede beobachtete Antwort (= Reaktion) einer Vp ist von drei Komponenten abhängig: a) Eigenschaften der Person (z.B. Fähigkeiten)b) Eigenschaften des Items (z.B. Schwierigkeit)c) Zufall: unkontrollierbare, fluktuierende Einflüsse, die beim "Messen" in den Sozialwissenschaften immer zu erwarten sind.
- Die manifeste Variable (Antworten der Personen auf Items) sind Indikatoren einer postulierten latenten Fähigkeits- oder Eigenschaftsdimension
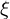(sprich: Xi) (mit Hilfe der manifesten Variable wird auf die latente Dimension rückgeschlossen) - Der Zusammenhang zwischen manifester Variable und latenter Dimension ist systematisch, er wird für jedes einzelne Item i durch die Itemcharakteristik (Funktion) hergestellt:
- Zusammenhänge zwischen den manifesten Variablen (z.B. 2 Antworten 2 verschiedener Items) sind nicht Ausdruck direkter Abhängigkeit zwischen den einzelnen Verhaltensweisen, sondern Ausdruck ihrer Abhängigkeit von einer, allen manifesten Variablen gemeinsam zugrunde liegenden latenten Dimension.
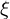- Jedes item ist mit der latenten Dimension durch eine eindeutigen Funktion verknüpft. In Abhängigkeit von v (Fähigkeit der Person v) hat jede Person eine bestimmte _Wahrscheinlichkeit ein Item zu lösen (probabilistischer Charakter der Item-Response-Theory).- Person mit gleicher Fähigkeitsgraden (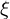) haben auch dieselbe Chance fi(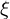), die Aufgabe i zu lösen.- Die Item Lösungswahrscheinlichkeit soll nie 0 oder 1 erreichen, weil der Schäwcste einmal Glück haben kann bzw. dem Besten ein Fehler unterlaufen kann.Wenn diese Betrachtung richtig ist und somit einelatente Dimension existiert, dann könnte man diese latente Dimension (statistisch) konstant halten (herauspartialisieren).
Es folgt: nach Konstanthaltung müssten die Zusammenhänge zwischen den manifesten Variablen verschwinden - lokal stochastische Unabhängigkeit
d.h. Die Wahrscheinlichkeit, dass eine Vp mit Fähigkeit
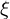beide Items (i und j) löst ist gleich dem Produkt aus der Wahrscheinlichkeit der Einzelreaktionen, nämlich der Wahrscheinlichkeit Item i zu lösen und der Wahrscheinlichkeit Item j zu lösen. Aus der lokalen stochastischen Unabhängigkeit folgt auch insbesondere, dass die Antworten einer Person auf ein Item nicht von Antworten auf andere Items abhängen darf. Zusätzlich wird im Rasch Modell angenommen, dass die Antworten verschiedene Personen__ voneinander stochastisch unabhängig sind (d.h. Schummeln verboten - beeinträchtigt die empirische Modellgeltung).
Tags: Rasch-Modell
Quelle: S44
Quelle: S44
Was bedeutet die lokale stochastische Unabhängigkeit beim RM?
Zusammenhänge zwischen den manifesten Variablen (z.B. 2 Antworten 2 verschiedener Items) sind nicht Ausdruck direkter Abhängigkeit zwischen den einzelnen Verhaltensweisen, sondern Ausdruck ihrer Abhängigkeit von einer, allen manifesten Variablen gemeinsam zugrunde liegenden latenten Dimension.
Wenn diese Betrachtung richtig ist und somit einelatente Dimension existiert, dann könnte man diese latente Dimension (statistisch) konstant halten (herauspartialisieren).
Es folgt: nach Konstanthaltung müssten die Zusammenhänge zwischen den manifesten Variablen verschwinden - lokal stochastische Unabhängigkeit
Formel:
d.h. Die Wahrscheinlichkeit, dass eine Vp mit Fähigkeit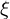 beide Items (i und j) löst ist gleich dem Produkt aus der Wahrscheinlichkeit der Einzelreaktionen, nämlich der Wahrscheinlichkeit Item i zu lösen und der Wahrscheinlichkeit Item j zu lösen. Aus der lokalen stochastischen Unabhängigkeit folgt auch insbesondere, dass die Antworten einer Person auf ein Item nicht von Antworten auf andere Items abhängen darf.
Zusätzlich wird im Rasch Modell angenommen, dass die Antworten verschiedene Personen voneinander stochastisch unabhängig sind (d.h. Schummeln verboten - beeinträchtigt die empirische Modellgeltung).
Wenn diese Betrachtung richtig ist und somit einelatente Dimension existiert, dann könnte man diese latente Dimension (statistisch) konstant halten (herauspartialisieren).
Es folgt: nach Konstanthaltung müssten die Zusammenhänge zwischen den manifesten Variablen verschwinden - lokal stochastische Unabhängigkeit
Formel:
d.h. Die Wahrscheinlichkeit, dass eine Vp mit Fähigkeit
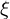beide Items (i und j) löst ist gleich dem Produkt aus der Wahrscheinlichkeit der Einzelreaktionen, nämlich der Wahrscheinlichkeit Item i zu lösen und der Wahrscheinlichkeit Item j zu lösen. Aus der lokalen stochastischen Unabhängigkeit folgt auch insbesondere, dass die Antworten einer Person auf ein Item nicht von Antworten auf andere Items abhängen darf. Zusätzlich wird im Rasch Modell angenommen, dass die Antworten verschiedene Personen voneinander stochastisch unabhängig sind (d.h. Schummeln verboten - beeinträchtigt die empirische Modellgeltung).
Tags: lokale stochastische Unabhängigkeit, Rasch-Modell
Quelle: S44
Quelle: S44
Wovon soll - laut RM - das Lösen einer Aufgabe abhängen?
Die Wahrscheinlichkeit einer Aufgabe zu lösen [p ( + ӏ ξ v , σi)] soll abhängen von …
- … Fähigkeit der Person ξv (ξ v ist der zu schätzende Fähigkeitsparameter der Person v)
- … Schwierigkeit d. Aufgabe σi (σi ist der zu schätzende Itemparameter für Item i)
- … sonst nichts, d.h. andere Itemauswahl (aus dem Itempool) oder andere Personenauswahl (aus der Grundgesamtheit) sollen keinen systematischen Einfluss auf die zu schätzenden Parameter haben.
Tags: Rasch-Modell
Quelle: S44
Quelle: S44
Wie ist die Datenmatrix zur Schätzung der Parameter im Rasch-Modell aufgebaut?
Dichotomes logistische Modell von RASCH (1960)
Die statistische Information zur Schätzung der Parameter findet sich in der folgenden Datenmatrix (Modellgeltung vorausgesetzt):
Jede Person ist im RM durch ihre Position
v auf der latenten Dimension charakterisiert. v ist ein "Personen(fähigkeits)parameter", der - wie andere statistische Parameter auch - erst geschätzt werden muss.
Analoges gilt für die Itemparameter: Jedes Item ist durch seine Position (Lage)
i auf der latenten Dimension charaktersisiert. i ist ein "Item(schwierigkeits)parameter", der erst geschätzt werden muss.
Die statistische Information zur Schätzung der Parameter findet sich in der folgenden Datenmatrix (Modellgeltung vorausgesetzt):
Jede Person ist im RM durch ihre Position
v auf der latenten Dimension charakterisiert. v ist ein "Personen(fähigkeits)parameter", der - wie andere statistische Parameter auch - erst geschätzt werden muss.Analoges gilt für die Itemparameter: Jedes Item ist durch seine Position (Lage)
i auf der latenten Dimension charaktersisiert. i ist ein "Item(schwierigkeits)parameter", der erst geschätzt werden muss. Tags: Rasch-Modell
Quelle: VO06
Quelle: VO06
Was ist die Grundgleichung des Rasch-Modells und auf welcher mathematischen Funktion basiert diese?
Erkläre dies anhand eines Beispiels..
Erkläre dies anhand eines Beispiels..
Welche mathematische Funktion entspricht nun den durch Rasch aufgestellten Forderungen und Grundannahmen?
Die sog. logistische Funktion
Daher kommt Rasch zu folgender Grundgleichung des RM (Darstellung mit logarithmierten Parametern)
Im RM wird also die Lösungswahrscheinlichkeit als logistische Funktion der Differenz d von Personenfähigkeit und Itemschwierigkeit (v - i) beschrieben.
Berechnungsbeispiel einer Itemcharakteristik
Die Festlegung der Struktur eines probabilistischen Testmodells besteht in der Spezifikation der Funktionen fi (ξ). Sind diese Funktionen bekannt, dann können die Parameter geschätzt werden.
Anmerkung
Die sog. logistische Funktion
Daher kommt Rasch zu folgender Grundgleichung des RM (Darstellung mit logarithmierten Parametern)
Im RM wird also die Lösungswahrscheinlichkeit als logistische Funktion der Differenz d von Personenfähigkeit und Itemschwierigkeit (
v - i) beschrieben.Berechnungsbeispiel einer Itemcharakteristik
Die Festlegung der Struktur eines probabilistischen Testmodells besteht in der Spezifikation der Funktionen fi (ξ). Sind diese Funktionen bekannt, dann können die Parameter geschätzt werden.
Anmerkung
- Rasch-Modell benötigt dichotome Testaufgaben.
- p(+): Wahrscheinlichkeit ein Item zu lösen; hängt nicht davon ab, wie groß v und wie groß i ist, sondern lediglich von der Differenz v-i
- p(+) = 0,5: wenn v = i; das ist auch inhaltlich sinnvoll, weil Person v dann gleich fähig ist wie das Item i schwierig ist (= Lösungsschwierigkeit 1/2)
Tags: Rasch-Modell
Quelle: S45
Quelle: S45
Was sind Kennzeichen des Rasch-Modells (ergänzende Bemerkungen)?
- Das RM ist das einzige probabilistische Testmodell, das spezifisch objektive Vergleiche ermöglicht und dadurch "Stichprobenunabhängigkeit" der Messung realisiert
- Eindimensionalität der Testaufgaben Für alle Items hängt die Lösungswahrscheinlichkeit nur über den Parameter
- Erschöpfende Statistik Für jede Person v stellt die Anzahl gelöster Aufgaben (rv ) "Personenrandsumme" oder Rohwert) eine sog. erschöpfende Statistik für ihren unbekannten Personenparameter dar. (Analoges gilt für die Itemrandsummen und die unbekannten Itemparameter)Für die Schätzung des Personenparameters sind sämtliche relevante Informationen in rv enthalten; d.h. es ist also nur mehr von Bedeutung, wie viele der Testaufgaben von einer Person gelöst werden, nicht aber welche.
v von den Jeweiligen Testpersonen ab.Alle "latente" Personenmerkmale, die (neben den Itemeigenschaften) die Reaktionen einer Testperson bestimmten, sind vollständig in diesem einen Parameter "zusammengefasst".Eine Verletzung der Eindimensionalität würde bedeuten, dass gewisse Persönlichkeitsmerkmale (z.B. Geschlecht, Alter,...) bei verschiedenen Aufgaben mit unterschiedlicher Gewichtung zur Reaktion beitragen.Wünscht man einen Test, bei dem der Testrohwert (rv) interpretiert werden kann, so mus für diesen Test das Rasch-Modell gelten (und dies ist mathematisch beweisbar)!
Beachte: Nahezu alle herkömmlichen Fähigkeitstests die mittels KTT entwickelt wurden, interpretieren den Testrohwert (=Summe der gelösten Aufgaben), jedoch ohne zu überprüfen, ob das korrekt ist!
Tags: Rasch-Modell
Quelle: S46
Quelle: S46
Was sind die Konsequenzen für die Anwendungspraxis bei
Gültigkeit des RM?
Gültigkeit des RM?
- Test misst für alle Personen (begabte/unbegabte; m/w [gender fairness!]; jüngere/ältere, etc.) dieselbe latenten Dimension (sprich: die Items sind Rasch homogen oder eindimensional).
- Die Rohwerte (Vpn‐Randsummen) enthalten die gesamten Informationen, die zur Schätzung der Personenfähigkeitsparameter notwendig sind. Personen mit gleichen Rohwerten sind nachweislich auch gleich fähig. Fragen, welche speziellen Aufgaben von Vpn mit gleichem RW gelöst bzw. nicht gelöst wurden, brauchen nicht mehr gestellt zu werden, da sie – mathematisch beweisbar – keinen diagnostischen „Mehr‐Wert“ liefern.
- Der Zusammenhang zwischen den rangskalierten Rohwerten und den intervallskalierten Fähigkeitsparametern ist empirisch begründet (d.h. durch Daten untermauert und durch Modelltests abgesichert). Damit ist eine intervallskalierte Fähigkeitsskala etabliert und man kann von „echter Messung“ der zugrunde liegenden Eigenschaft (Dimension) sprechen.
Tags: Rasch-Modell
Quelle: VO06
Quelle: VO06
Was sind die Vorzüge des Rasch-Modells?
Mittels Modellgeltungskontrollen kann im RM geprüft werden, ob die im Modell enthaltenen Annahmen für einen empirisch gegebenen Datensatz gelten oder nicht. Wenn das Modell empirisch gilt, darf gefolgert werden
ABER:
Der Aufwand für Testkonstruktion auf Basis des Rasch Modells ist weitaus größer als auf Basis der klassischen Testtheorie. (Das mag zum Teil erklären, dass auch heute noch - trotz unbestrittener Vorzüge der Item-Response-Theorie - Testkonstruktionen mittels klassischer Testtheorie vorgenommen werden.)
- Der Test misst für alle Testpersonen (jüngere/ältere; begabte/unbegabte; männliche/weibliche; etc.) dieselbe latente Fähigkeitsdimension (dasselbe Konstrukt). Die Testaufgaben sind in diesem Sinne eindimensional und messen fair (z.B. auch Gender-Fair)
- Die Personenparameter (Fähigkeitsparameter) kennzeichnen die Fähigkeitsgrade der Personen. Sie liegen auf einer Intervallskala und sind unabhängig davon, welche und wie viele Items im Test vorgegeben wurden.
- Die Itemparameter (Aufgabenschwierigkeitsparameter) liegen auf derselben Intervallskala wie die Personenparameter. Sie kennzeichnen die Schwierigkeitsgrade von Items und sind unabhängig davon, welche Personengruppen getestet werden.
- Zur Bestimmung der Personenfähigkeiten genügt es zu wissen, wie viele Items gelöst wurden und nicht welche Testitems gelöst wurden.
- Die Reihenfolge, in der die Items vorgegeben werden spielt für das Testergebnis keine Rolle.
- Fähigkeitsangepasstes Testen (sog. Adaptives Testen) ist optional möglich, wenn ein genügend großer Aufgabenpool vorhanden ist.
- Veränderungen können gemessen werden. In der klassischen Testtheorie sagt eine Verbesserung um 1 Rohwertpunkt nicht aus um wieviel sich die Person verbessert hat.
ABER:
Der Aufwand für Testkonstruktion auf Basis des Rasch Modells ist weitaus größer als auf Basis der klassischen Testtheorie. (Das mag zum Teil erklären, dass auch heute noch - trotz unbestrittener Vorzüge der Item-Response-Theorie - Testkonstruktionen mittels klassischer Testtheorie vorgenommen werden.)
Tags: Rasch-Modell
Quelle: S47
Quelle: S47
Was ist der 3DW?
Und welche Ergebnisse zeigte die Überprüfung hinsichtlich des Rasch-Modells?
Und welche Ergebnisse zeigte die Überprüfung hinsichtlich des Rasch-Modells?
Ein Rasch‐skalierter Test zur Messung des räumlichen
Vorstellungsvermögens (Gittler, 1990)
Testinstruktion(verkürzt): Jeder Würfel hat sechs verschiedene Muster, nur drei davon kann man sehen. Prüfen Sie, ob einer der Würfel A bis F derselbe Würfel sein kann, wie der links gezeigte Würfel X, oder ob die Antwort G „kein Würfel richtig“ zutreffend ist. Sollte eine Aufgabe zu schwierig sein, dann wählen Sie die Antwort H „Ich weiß die Lösung nicht“.
Empirisch bestimmter Zusammenhang zwischen rangskalierten Testrohwerten und intervallskalierten Fähigkeitsparametern im 3DW
Weitere empirische Ergebnisse zum 3DW:
li.: Grafischer Modelltest (nieder/hoch)
re: theoretische und empirische Item Response Functions
Signifikante Leistungsänderungen
Vorstellungsvermögens (Gittler, 1990)
Testinstruktion(verkürzt): Jeder Würfel hat sechs verschiedene Muster, nur drei davon kann man sehen. Prüfen Sie, ob einer der Würfel A bis F derselbe Würfel sein kann, wie der links gezeigte Würfel X, oder ob die Antwort G „kein Würfel richtig“ zutreffend ist. Sollte eine Aufgabe zu schwierig sein, dann wählen Sie die Antwort H „Ich weiß die Lösung nicht“.
Empirisch bestimmter Zusammenhang zwischen rangskalierten Testrohwerten und intervallskalierten Fähigkeitsparametern im 3DW
Weitere empirische Ergebnisse zum 3DW:
li.: Grafischer Modelltest (nieder/hoch)
re: theoretische und empirische Item Response Functions
Signifikante Leistungsänderungen
Tags: Beispiel, Rasch-Modell
Quelle: VO06
Quelle: VO06
Was sind die Anwendungsbespiele für das Rasch-Modell im Überblick?
- Item-Bias Skalen‐ bzw. Testkonstruktion
- Transkulturelles Testen Entwicklung und Evaluierung von „culture fair“ Tests:
- Computerisiertes Adaptives Testen (CAT) Entwicklung von Aufgabenpools für das computerisierte adaptive Testen (= fähigkeitsangepasstes Testen)
- Psychometrische Qualitätskontrolle von Tests
- Veränderungsmessung Veränderungsmessung im Prä‐ / Posttest Design:
Tags: Anwendung, Rasch-Modell
Quelle: S48
Quelle: S48
Inwiefern unterstützt das Rasch-Modell bei der Skalen und Testkonstruktion?
(Aufwand hoch im Vergleich zur KTT wegen der zahlreichen Modellprüfungen an großen Datensätzen)
Ein Item ist als verzerrt od. unfair anzusehen, wenn seine IC-Kurve in zwei unabhängig von diesem Item definierten Gruppen verschieden ist; ein Test wird unfair sein, wenn zumindest ein Item "biased" ist.
(Beachte: Die Definition von Item-Homogenität oder Item-Bias erfolgt stets im Rahmen eines bestimmten Modells.)
- Entdeckung von Item‐Bias: Sofern einzelne Items eines Tests Gruppen von Personen benachteiligen spricht man von Item‐Bias oder "Differential Item Functioning" (kurz: DIF).
- Derartige DIF‐Items bevorzugen ungerechtfertigter Weise Personengruppen (z.B. Begabungsgruppen, Geschlechtergruppen, ethnische Gruppen, Alters‐ oder Ausbildungsgruppen etc.) und stellen somit eine Gefahr für die Testinterpretation dar. Allgemein kann man sagen: Ein Test, der DIF‐Items enthält, misst nicht fair.
- Fehlinterpretationen, Verminderung der Messeffizienz (Reliabilität, Validität etc.) des gesamten Tests.
Ein Item ist als verzerrt od. unfair anzusehen, wenn seine IC-Kurve in zwei unabhängig von diesem Item definierten Gruppen verschieden ist; ein Test wird unfair sein, wenn zumindest ein Item "biased" ist.
(Beachte: Die Definition von Item-Homogenität oder Item-Bias erfolgt stets im Rahmen eines bestimmten Modells.)
Tags: Rasch-Modell
Quelle: S48
Quelle: S48
Inwiefern unterstützt das Rasch-Modell das transkulturelle Testen?
Entwicklung und Evaluierung von „culture fair“ Tests:
(Anmerkung: Häufig werden nonverbal-bildhaft dargebotene Testaufgaben, zu deren Lösung keine speziellen Kulturtechniken wie Lesen oder Mathematik nötig sind, als Culture-Fair eingestuft - dies reicht aus Sicht der modernen Psychometrie nicht aus. Es muss empirisch nachgewiesen werden.)
- Nachweis der Gültigkeit des RM in der „Ausgangskultur“
- Sorgfältige Übersetzung bzw. Übertragung eines Tests in andere Sprache
- Nachweis der Gültigkeit des RM in der „Zielkultur“
- Nachweis Gültigkeit des Rasch Modells über beide Kulturen: Im Sinne des RMs ist ein Test dann als culture fair zu bezeichnen, wenn alle Items in den untersuchten Kulturen gemeinsam Rasch homogen sind.
(Anmerkung: Häufig werden nonverbal-bildhaft dargebotene Testaufgaben, zu deren Lösung keine speziellen Kulturtechniken wie Lesen oder Mathematik nötig sind, als Culture-Fair eingestuft - dies reicht aus Sicht der modernen Psychometrie nicht aus. Es muss empirisch nachgewiesen werden.)
Tags: Rasch-Modell
Quelle: S48
Quelle: S48
Inwiefern unterstützt das Rasch-Modell das computerisierte Adaptive Testen (CAT)? Vor- und Nachteile von CAT?
Entwicklung von Aufgabenpools für das computerisierte
adaptive Testen (= fähigkeitsangepasstes Testen):
Es werden individuell unterschiedlich schwierige Aufgaben aus dem Itempool (während der Computertestung) vorgegeben, die dem Fähigkeitsniveau der jeweiligen Vp bestmöglich entsprechen.
Die Auswahl der Items erfolgt durch den Computer - Nach jeder Itembeantwortung wird der aktuelle Fähigkeitsparameterv der Vp geschätzt und danach das bestpassende Item (= informativste Item mit i ungefähr v) aus dem Poo vorgegeben.
Positive Konsequenzen des CAT:
Nachteile:
adaptive Testen (= fähigkeitsangepasstes Testen):
Es werden individuell unterschiedlich schwierige Aufgaben aus dem Itempool (während der Computertestung) vorgegeben, die dem Fähigkeitsniveau der jeweiligen Vp bestmöglich entsprechen.
Die Auswahl der Items erfolgt durch den Computer - Nach jeder Itembeantwortung wird der aktuelle Fähigkeitsparameter
v der Vp geschätzt und danach das bestpassende Item (= informativste Item mit i ungefähr v) aus dem Poo vorgegeben.Positive Konsequenzen des CAT:
- Wenige "unnütze" Items im Test (zu leicht bzw. schwere werden vermieden)
- Höhere Messgenauigkeit bei ev. weniger Items (kürzere Testdauer)
- Auch in Extrembereichen kann präziser gemessen werden
- Testabbruch kann auf diagnostische Anforderungen eingestellt werden (z.B. nur grobes Screening oder präzise Messung)
- Testsicherheit und Testfairness erhöht, weil "Testknackermethoden" weitgehend unwirksam (z.B. Auswendiglernen eines Antwortvektors nicht möglich, weil jede Testperson andere Items vorgelegt bekommt)
- Abschauen bzw. Schummeln bei Gruppentestungen unterbunden
- Die Bekanntgabe des Itemtyps der im Pool enthalten Aufgaben (nicht die Poolaufgabe selbst) zur Testvorbereitung ist möglich. (Reduktion von Testangst)
Nachteile:
- Massiv erhöhter Testkonstruktionsaufwand für den Testkonstrukteur bei der Entwicklung eines Rasch-homogenen Itempools
Tags: CAT, Rasch-Modell
Quelle: S49
Quelle: S49
Inwiefern unterstützt das Rasch-Modell die psychometrische Qualitätskontrolle von Tests?
z.B. Frage, ob zwei ähnliche Tests auch dasselbe Konstrukt erfassen.
Wenn Tests ähnliche latente Dimensionen erfassen, ist es aus testökonomischer Sicht nicht gerechtfertigt, sie gemeinsam in einer Testbatterie zu belassen.
Im klassischen Ansatz wird die Gleichartigkeit von Tests mittels Korrelationen ermittelt, die jedoch keine konklusive (eindeutige) Aussage ermöglichen.
Bei gemeinsamer Verrechnung der Tests im RM ist der Modelltests zwischen den Itemgruppen (Reasoning-Test WMT räumlicher Anteile vs. Raumvorstellungstest 3DW) signifikant - Tests messen nicht dieselbe Subdimension des Konstrukts Raumvorstellung.
Aus dieser Überprüfung mit dem Rasch-Modell können positive Aussagen zum Nutzen und zur Konstruktvalidität der Tests abgeleitet werden.
Wenn Tests ähnliche latente Dimensionen erfassen, ist es aus testökonomischer Sicht nicht gerechtfertigt, sie gemeinsam in einer Testbatterie zu belassen.
Im klassischen Ansatz wird die Gleichartigkeit von Tests mittels Korrelationen ermittelt, die jedoch keine konklusive (eindeutige) Aussage ermöglichen.
Bei gemeinsamer Verrechnung der Tests im RM ist der Modelltests zwischen den Itemgruppen (Reasoning-Test WMT räumlicher Anteile vs. Raumvorstellungstest 3DW) signifikant - Tests messen nicht dieselbe Subdimension des Konstrukts Raumvorstellung.
Aus dieser Überprüfung mit dem Rasch-Modell können positive Aussagen zum Nutzen und zur Konstruktvalidität der Tests abgeleitet werden.
Tags: Psychometrie, Rasch-Modell, Test
Quelle: S50
Quelle: S50
Inwiefern unterstützt das Rasch-Modell die Veränderungsmessung?
Veränderungsmessung im Prä‐ / Posttest Design:
- Der Hauptvorteil Rasch homogener Tests liegt in der Intervallskaleneigenschaft der Personenfähigkeitsparameter und der Itemschwierigkeitsparameter. (Testrohwerte beim klassischen Ansatz sind i.A. nur rangskaliert)
- Unter zusätzlicher Verwendung eines weiteren IRT‐Modells (lineares Logistisches Modell, LLTM) können die Effekte spezifiziert werden (vgl. Beispiele hinten).
Tags: Rasch-Modell
Quelle: S50
Quelle: S50
Was sind Anwendungsbeispiele für Veränderungsmessungen?
Anwendungsbeispiel 1 zum linearen logistischen
Modell (LLTM): Veränderungsmessung
Keine signifikanten Unterschiede zwischen Kaugummikau-Gruppe und Kontrollgruppe.
Anwendungsbeispiel 2 zum LLTM: Veränderungsmessung
„Pheromone Exposure Impairs Spatial Task Performance in Young men“
Modell (LLTM): Veränderungsmessung
Keine signifikanten Unterschiede zwischen Kaugummikau-Gruppe und Kontrollgruppe.
Anwendungsbeispiel 2 zum LLTM: Veränderungsmessung
„Pheromone Exposure Impairs Spatial Task Performance in Young men“
- Männer mussten Aufgaben des Raumvorstellungstests (3DW) bearbeiten)
- Dazwischen mussten sie eine Atemmaske aufsetzen: - Kontrollgruppe: nur Luft- Versuchsgruppe: Pheromone (unter der Riechschwelle)
- Hypothese - Androgynie-Vorstellung der Raumverstellung: weibliche Männer und männliche Frauen haben bessere Raumvorstellungsfähigkeiten.
- Indirekt über die Pheromone wird das Testosterone erhöht.
- Ergebnis: es gab tatsächlich signifikante Veränderungen der Leistung – die Pheromone-Gruppe haben im 2. Teil des Leistungstest signifikant schlechtere Ergebnisse erzielt.
Tags: Beispiel, Rasch-Modell
Quelle: VO06
Quelle: VO06
Kartensatzinfo:
Autor: ZoeSzapary
Oberthema: Differenzielle Psychologie
Thema: Alle Kapitel
Schule / Uni: Universität Wien
Ort: Wien
Veröffentlicht: 11.12.2019
Schlagwörter Karten:
Alle Karten (221)
16 PF (9)
Abgrenzung (1)
Adoptionsmethode (1)
Aggregation (1)
Aktivität (2)
Analysatoren (1)
Anlage/Umwelt (13)
Anwendung (4)
Army-Alpha-Test (1)
Ausdruck (1)
Beispiel (3)
Big Five (11)
Binet (5)
Carroll (2)
CAT (1)
Cattell (17)
CHC (2)
Darwin (2)
Definition (13)
EEG (2)
Einstellungstyp (1)
Entstehung (1)
Entwicklung (1)
Erblichkeit (1)
Evolution (1)
Experiment (4)
Extraversion (7)
Eysenck (14)
Faktorenanalyse (11)
Faktorenmodell (1)
Fehr (1)
Felabhängigkeit (1)
Feldabhängigkeit (2)
fMRT (1)
Forschung (22)
Fragebogen (1)
Funktionstyp (1)
Galton (3)
Gardner (3)
Geschichte (11)
Gray (1)
HAWIE (1)
Hochbegabung (4)
Hofstätter (2)
Horn (3)
Intelligenz (41)
Intelligenzmodelle (17)
Intervention (1)
Jung (6)
Kagan (1)
Kelly (4)
Korrelation (5)
Kretschmer (1)
Kritik (12)
Mendel (1)
mental Speed (3)
mental speed (1)
Merkmal (1)
Methoden (22)
Neurotizismus (3)
Normalverteilung (1)
Norman (1)
Objektivität (1)
Persönlichkeit (36)
Persönlickeit (1)
PET (1)
Prozessmodell (1)
Psychographie (2)
Psychologie (2)
Psychometrie (1)
Psychotizismus (2)
Quasi-Experiment (1)
R/S Konstrukt (4)
Rasch-Modell (17)
Reflexivität (1)
Regression (2)
Repression (2)
Rogers (7)
Sensitization (2)
Sheldon (1)
Simon-Binet-Test (1)
Skala (1)
Spearman (4)
Stabilität (1)
Stern (10)
Sternberg (6)
Stimmung (1)
Strelau (3)
Streuung (1)
Struktur (1)
Superfaktoren (1)
Terman (2)
Test (10)
Testung (1)
Theorie (6)
Thurstone (2)
TMI (3)
Trait-Modell (7)
Typenlehre (1)
Unterschiede (1)
Variable (1)
Varianz (4)
Varianzzerlegung (1)
Vernon (2)
Wahrnehmung (1)
Wechsler (2)
Witkin (1)
working memory (2)
Zuckerman (3)
Zwillingsmethode (5)
