Wie lauten die 4 klassischen Konstruierbarkeitsfragen der griechischen Antike?
1) Winkeldreiteilung:
Zu einem beliebigen gegebenen Winkel soll ein der Größe
soll ein der Größe 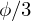 konstruiert werden.
konstruiert werden.
2) Delisches Problem:
Zu einem gegebenen Würfel der Kantenlänge a ist ein Würfel doppelten Volumens gesucht. Frage: Ist die neue Kantenlänge mit Zirkel und Lineal konstruierbar?
mit Zirkel und Lineal konstruierbar?
3) Quadratur des Kreises
Zu einem gegebenen Kreis soll ein Quadrat mit gleichem Flächeninhalt konstruiert werden. Frage: Ist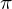 mit Zirkel und Lineal konstruierbar?
mit Zirkel und Lineal konstruierbar?
4) Konstruktion eines regelmässigen n-Ecks
Für welche n ist die Konstruktion eines regelmässigen n-Ecks möglich?
Zu einem beliebigen gegebenen Winkel
 soll ein der Größe
soll ein der Größe 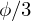 konstruiert werden.
konstruiert werden.2) Delisches Problem:
Zu einem gegebenen Würfel der Kantenlänge a ist ein Würfel doppelten Volumens gesucht. Frage: Ist die neue Kantenlänge
 mit Zirkel und Lineal konstruierbar?
mit Zirkel und Lineal konstruierbar?3) Quadratur des Kreises
Zu einem gegebenen Kreis soll ein Quadrat mit gleichem Flächeninhalt konstruiert werden. Frage: Ist
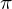 mit Zirkel und Lineal konstruierbar?
mit Zirkel und Lineal konstruierbar?4) Konstruktion eines regelmässigen n-Ecks
Für welche n ist die Konstruktion eines regelmässigen n-Ecks möglich?
Wie lautet das Kriterium von Eisenstein?
Sei 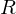 ein Integritätsring und sei:
ein Integritätsring und sei:

ein primitives Polynom aus . Gibt es dann ein Primelement
. Gibt es dann ein Primelement 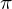 mit
mit
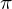 teilt nicht
teilt nicht ,
,  teilt nicht
teilt nicht  ,
,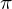 teilt
teilt  ,
,
so ist irreduzibel in
irreduzibel in  . Im Falle eines faktoriellen Ringes
. Im Falle eines faktoriellen Ringes 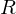 ist f dann auch irreduzibel in
ist f dann auch irreduzibel in  wobei
wobei  den Quotientenkörper von
den Quotientenkörper von 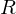 bezeichne.
bezeichne.
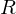 ein Integritätsring und sei:
ein Integritätsring und sei:
ein primitives Polynom aus
 . Gibt es dann ein Primelement
. Gibt es dann ein Primelement 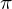 mit
mit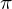 teilt nicht
teilt nicht ,
,  teilt nicht
teilt nicht  ,
,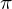 teilt
teilt  ,
, so ist
 irreduzibel in
irreduzibel in  . Im Falle eines faktoriellen Ringes
. Im Falle eines faktoriellen Ringes 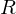 ist f dann auch irreduzibel in
ist f dann auch irreduzibel in  wobei
wobei  den Quotientenkörper von
den Quotientenkörper von 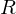 bezeichne.
bezeichne.Flashcard set info:
Author: Willi Kufalt
Main topic: Mathematik
Topic: Algebra
Published: 26.03.2010
Card tags:
All cards (12)
no tags



 heißt normal, wenn für jedes
heißt normal, wenn für jedes gilt:
gilt: ein Polynom vom Grade
ein Polynom vom Grade  . Ein Erweiterunsgkörper E von K heißt Zerfällungskörper von f über K, wenn alle Nullstellen von f in L liegen, d.h. wenn es
. Ein Erweiterunsgkörper E von K heißt Zerfällungskörper von f über K, wenn alle Nullstellen von f in L liegen, d.h. wenn es  gibt mit
gibt mit 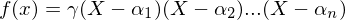 und
und 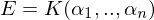 .
. ist
ist  .
. ist definiert als:
ist definiert als: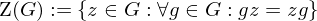
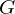 eine endliche Gruppe.
eine endliche Gruppe.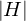 ein Teiler von
ein Teiler von  .
.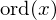 eines Elementes
eines Elementes  von
von 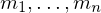 paarweise teilerfremd und
paarweise teilerfremd und 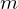 ihr Produkt, dann ist der Faktorring
ihr Produkt, dann ist der Faktorring  isomorph zum Produktring
isomorph zum Produktring 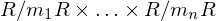 durch den Isomorphismus:
durch den Isomorphismus: heißt Ideal, wenn gilt:
heißt Ideal, wenn gilt: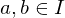 gilt auch
gilt auch  .
.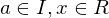 , gilt:
, gilt: 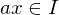 .
.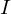 ist eine Untergruppe von
ist eine Untergruppe von 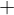
 hat den Inhalt 2.
hat den Inhalt 2.