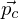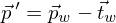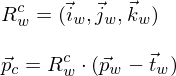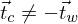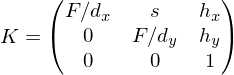Rendering-Equation
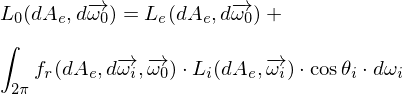

 Oberflächenelement
Oberflächenelement Strahlungsrichtung
Strahlungsrichtung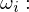 Einfallsrichtungen
Einfallsrichtungen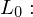 Das gesamte Licht, das von einem Oberflächenelement in eine Richtung ausgestrahlt wird
Das gesamte Licht, das von einem Oberflächenelement in eine Richtung ausgestrahlt wird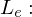 Licht, das von dem Oberflächenelement in die Richtung
Licht, das von dem Oberflächenelement in die Richtung 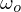 emittiert wird
emittiert wird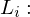 Licht, das von allen möglichen Einfallsrichtungen einfällt und in
Licht, das von allen möglichen Einfallsrichtungen einfällt und in 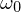 reflektiert wird
reflektiert wird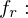 6-dimensionale BRDF
6-dimensionale BRDFWikipedia
Welche Koordinatensysteme gibt es und wie sind sie definiert?
Weltkoordinatensystem (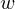 ):
):
Es ist ein 3D System. Hiermit werden Objekte und Kameras in der Szene lokalisiert, denn es beschreibt einen festen Referenzpunkt. Ursprung und Orientierung der Achsen können beliebig gewählt werden. (euklidisch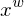 , homogen
, homogen 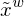 )
)
Objektkoordinatensystem:
Es ist ein 3D System. Beschreibt Objektpunkte. Wird in der Computergraphik verwendet, aber nicht im Rechnersehen.
Kamerakoordinatensystem ( ):
):
Es ist ein 3D System. Dieses System gehört zu einer (sich bewegenden) Kamera und definiert deren Position und Ausrichtung. Der Ursprung befindet sich im optischen Zentrum der Kamera. Die z-Achse entspricht der Blickrichtung, fällt also mit der optischen Achse der Kamera zusammen, die x- und
y-Achsen sind parallel zu den Zeilen und Spalten des Bildes.
Bildkoordinatensystem ( ):
):
Es ist ein 2D System. Koordinatensystem des Bildes, das auf der Bildebene in der Kamera dargestellt wird. Der Ursprung liegt ungefähr in der Bildmitte und ist gekennzeichnet als Punkt H. Die 2 Achsen sind parallel zur x- und y-Achse des Kamerakoordinatensystems . Dieses Bild ist nur virtuell, da es in einer Kamera auf einen CCD-Chip abgebildet, und damit in das Pixelkoordinatensystem überführt wird.
. Dieses Bild ist nur virtuell, da es in einer Kamera auf einen CCD-Chip abgebildet, und damit in das Pixelkoordinatensystem überführt wird.
Pixelkoordinatensystem ( ):
):
Es ist ein 2D System. Pixelkoordinatensystem p: Das System ist diskretisiert und der Ursprung liegt in der linken oberen Ecke. Die Achsen sind nicht 100% orthogonal zueinander.
Pixelkoordinatensystem (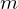 ):
):
Es ist ein 2D System. Der Ursprung liegt in der Bildmitte M.
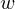 ):
):Es ist ein 3D System. Hiermit werden Objekte und Kameras in der Szene lokalisiert, denn es beschreibt einen festen Referenzpunkt. Ursprung und Orientierung der Achsen können beliebig gewählt werden. (euklidisch
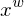 , homogen
, homogen 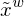 )
)Objektkoordinatensystem:
Es ist ein 3D System. Beschreibt Objektpunkte. Wird in der Computergraphik verwendet, aber nicht im Rechnersehen.
Kamerakoordinatensystem (
 ):
):Es ist ein 3D System. Dieses System gehört zu einer (sich bewegenden) Kamera und definiert deren Position und Ausrichtung. Der Ursprung befindet sich im optischen Zentrum der Kamera. Die z-Achse entspricht der Blickrichtung, fällt also mit der optischen Achse der Kamera zusammen, die x- und
y-Achsen sind parallel zu den Zeilen und Spalten des Bildes.
Bildkoordinatensystem (
 ):
):Es ist ein 2D System. Koordinatensystem des Bildes, das auf der Bildebene in der Kamera dargestellt wird. Der Ursprung liegt ungefähr in der Bildmitte und ist gekennzeichnet als Punkt H. Die 2 Achsen sind parallel zur x- und y-Achse des Kamerakoordinatensystems
 . Dieses Bild ist nur virtuell, da es in einer Kamera auf einen CCD-Chip abgebildet, und damit in das Pixelkoordinatensystem überführt wird.
. Dieses Bild ist nur virtuell, da es in einer Kamera auf einen CCD-Chip abgebildet, und damit in das Pixelkoordinatensystem überführt wird.Pixelkoordinatensystem (
 ):
):Es ist ein 2D System. Pixelkoordinatensystem p: Das System ist diskretisiert und der Ursprung liegt in der linken oberen Ecke. Die Achsen sind nicht 100% orthogonal zueinander.
Pixelkoordinatensystem (
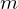 ):
):Es ist ein 2D System. Der Ursprung liegt in der Bildmitte M.
Tags: Klausur
Source:
Source:
Wie sieht die Modellgleichung fuer eine homogene Kamera (Lochkamera) definiert und welche Probleme gibt es? Wie Schaetzt man daraus die Kamerakonstante 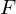 . Oder: Beschreiben Sie ein einfaches Kalibrierungsproblem
. Oder: Beschreiben Sie ein einfaches Kalibrierungsproblem
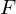 . Oder: Beschreiben Sie ein einfaches Kalibrierungsproblem
. Oder: Beschreiben Sie ein einfaches KalibrierungsproblemSei 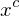 ... (i = 1, . N) eine Punktmenge aus der Kalibrierung zur Beschreibung des Kalibriermusters, und sei
... (i = 1, . N) eine Punktmenge aus der Kalibrierung zur Beschreibung des Kalibriermusters, und sei
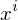 ... die korrespondierende Menge von Bildpunkten
... die korrespondierende Menge von Bildpunkten
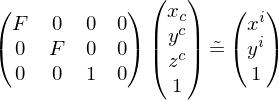
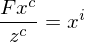
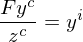
Problematisch ist es,
1. dass wir mit homogenen Gleichungen rechnen. Die Formel berechnet Abstaende und das geht mit homogonen Koordinaten nicht.
2. Nicht umformen. Die Modellgleichung nehmen und gluecklich sein.
Die Kamerakonstante wird uber folgende Formel ermittelt:
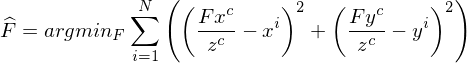
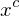 ... (i = 1, . N) eine Punktmenge aus der Kalibrierung zur Beschreibung des Kalibriermusters, und sei
... (i = 1, . N) eine Punktmenge aus der Kalibrierung zur Beschreibung des Kalibriermusters, und sei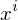 ... die korrespondierende Menge von Bildpunkten
... die korrespondierende Menge von Bildpunkten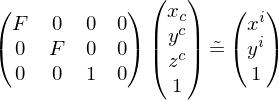
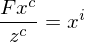
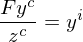
Problematisch ist es,
1. dass wir mit homogenen Gleichungen rechnen. Die Formel berechnet Abstaende und das geht mit homogonen Koordinaten nicht.
2. Nicht umformen. Die Modellgleichung nehmen und gluecklich sein.
Die Kamerakonstante wird uber folgende Formel ermittelt:
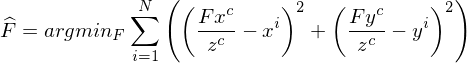
Tags: Klausur
Source:
Source:
Was ist das Doppelverhaeltnis und wie ist es beschrieben?
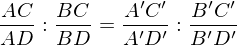
Einziges, projektives, invariates Mass.
Doppelverhaeltnis:
Das Verhaeltnis von zwei Linien unter projektiver Betrachtung
Tags: Klausur
Source:
Source:
Nenne die Grassmannsche Gesetze
1. Wir haben ein 3D Farbvalenzsystem. Bei vier gegebenen Farbvalenzen sind sie linear abhaengig. Drei koennen maximal unabhaengig sein.
2. nicht interessant fuer uns
3. stetige Veränderungen eines Mischungsoperanden.
bewirken stetige Veränderungen der Farbmischung.
Ansonsten wuerden die Farbraeume auch keinen Sinn machen.
2. nicht interessant fuer uns
3. stetige Veränderungen eines Mischungsoperanden.
bewirken stetige Veränderungen der Farbmischung.
Ansonsten wuerden die Farbraeume auch keinen Sinn machen.
Tags: Klausur
Source:
Source:
Wie sind die Primaervalenzen definiert?
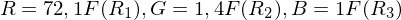
- Intensitäten nur relativ zueinander bestimmt
- Farbvalenz enthält keine absolute Helligkeitsinformation
- Summe
 ergibt Unbunt
ergibt Unbunt 
Tags: Klausur
Source:
Source:
Welche Farbräume gibt es?
-
 (Es gibt nicht DEN RGB). Er ist lineare.
(Es gibt nicht DEN RGB). Er ist lineare. -
 Realisiert technisch das, was die Retina bei uns macht. Gegenfarben... . Er ist lineare
Realisiert technisch das, was die Retina bei uns macht. Gegenfarben... . Er ist lineare -

 sind imaginär, da sie keinen tatsächlich exisiterenenden Gewichtungen entsprechen. Kann man real nicht darstellen. Ist das Normvalenzsystem. Er ist lineare
sind imaginär, da sie keinen tatsächlich exisiterenenden Gewichtungen entsprechen. Kann man real nicht darstellen. Ist das Normvalenzsystem. Er ist lineare - HSI und HSV (Sechseck). Sie entstehen aus nichtlineare Transformationen des RGB. Er ist nichtlineare
- Luv und Lab. Sie sind vollständig anders: Deren Abstände entsprechen dem menschlichen Farbunterschiedsempfinden. In diesen kann man sagen, was Farbähnlichkeit ist. Bestimmt wird die Differenz durch
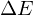 . Es ist die Differenz im Lab.
. Es ist die Differenz im Lab.
Tags: Klausur
Source:
Source:
Wie könnte eine Lösungsstrategie eines inversen Problems aussehen?
Sei
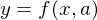
In diesem Fall:
Gelöst soll werden folgende Formel:
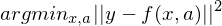
Zumeist, auch hier, wir eine Least-Square-Methode angewandt.
Wird diese angewandt, dann wird auch meistens die Gleichung regularisiert, um die Lösungen zu glätten.
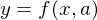
In diesem Fall:
- Eingabedaten:
 ,
, - Parameter / Randbedingungen:

- Ergebnisbild / Beobachtung:
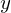
Gelöst soll werden folgende Formel:
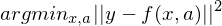
Zumeist, auch hier, wir eine Least-Square-Methode angewandt.
Wird diese angewandt, dann wird auch meistens die Gleichung regularisiert, um die Lösungen zu glätten.
Tags: Klausur
Source:
Source:
Was versteht man unter Regularisierung?
- Sie wird bspw. bei inversen Problemen Verwendet, um Ergebnisse zu glätten.
- Auch bekannt als Ridge-Regression
- Mittels Marginalisierung werden schlecht konditionierte Matrizen regularisiert, indem man zusätzliche Zeilen und Spalten hinzufügt.
- ... ?!
 Irgendwas mit nicht-degenerierte Differentialgleichung
Irgendwas mit nicht-degenerierte Differentialgleichung - In einem inversen Problem wird durch die Regularisierung das unterbestimmte System derart korrigiert, dass die Inverse bestimmt werden kann.
Beschreibe ein Klassifikationsmodell (Thema Bildverstehen)
Signal  Vorverarbeitung
Vorverarbeitung  Merkmalsextraktion
Merkmalsextraktion  Klassifikation
Klassifikation  Ergebnis
Ergebnis
Die Klassifikation kann noch durch einen Lernprozess
erweitert werden, dabei wird eine Strichprobe verwendet.
In dem Modell würde dann noch zusätzlich eine Kante in die Klassifikation einfließen:
Stichprobe Lernen
Lernen  Klassifikation
Klassifikation
Komplexer (Analyse durch Synthese):
Ich habe ein Bild, liefer mir das passende (synthetische) Bild.
 Vorverarbeitung
Vorverarbeitung  Merkmalsextraktion
Merkmalsextraktion  Klassifikation
Klassifikation  Ergebnis
ErgebnisDie Klassifikation kann noch durch einen Lernprozess
erweitert werden, dabei wird eine Strichprobe verwendet.
In dem Modell würde dann noch zusätzlich eine Kante in die Klassifikation einfließen:
Stichprobe
 Lernen
Lernen  Klassifikation
KlassifikationKomplexer (Analyse durch Synthese):
Ich habe ein Bild, liefer mir das passende (synthetische) Bild.
Tags: Klausur
Source:
Source:
Inverses Problem: Beispiel Poseerkennung
Poseerkennung: 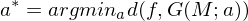
Objekterkennung: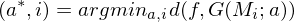
Mit:
In Worten:
Diejenige Kameraposition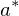 , für die die Bildentstehung mit einer Funktion der Graphik
, für die die Bildentstehung mit einer Funktion der Graphik 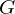 , einem gegebenen CG-Modell
, einem gegebenen CG-Modell  unter Annahme der Kameraposition
unter Annahme der Kameraposition  , verglichen mit dem aktuellen Bild
, verglichen mit dem aktuellen Bild  , den geringsten Abstand durch die Abstandsfunktion aufweist.
, den geringsten Abstand durch die Abstandsfunktion aufweist.
 dies beschreibt die Lösung eines inversen Problems mit Hilfe einer Vorwärtsfunktion. Wobei die Graphikfunktion die V.-Funktion darstellt.
dies beschreibt die Lösung eines inversen Problems mit Hilfe einer Vorwärtsfunktion. Wobei die Graphikfunktion die V.-Funktion darstellt.
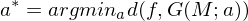
Objekterkennung:
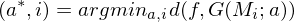
Mit:
- Bild

- Modell
 , Modelle
, Modelle 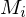
- Parametervektor
 , z.B.
, z.B. 
- Graphikfunktion
 liefert das Bild
liefert das Bild 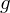
- Abstandsfunktion

In Worten:
Diejenige Kameraposition
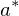 , für die die Bildentstehung mit einer Funktion der Graphik
, für die die Bildentstehung mit einer Funktion der Graphik 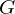 , einem gegebenen CG-Modell
, einem gegebenen CG-Modell  unter Annahme der Kameraposition
unter Annahme der Kameraposition  , verglichen mit dem aktuellen Bild
, verglichen mit dem aktuellen Bild  , den geringsten Abstand durch die Abstandsfunktion aufweist.
, den geringsten Abstand durch die Abstandsfunktion aufweist.  dies beschreibt die Lösung eines inversen Problems mit Hilfe einer Vorwärtsfunktion. Wobei die Graphikfunktion die V.-Funktion darstellt.
dies beschreibt die Lösung eines inversen Problems mit Hilfe einer Vorwärtsfunktion. Wobei die Graphikfunktion die V.-Funktion darstellt.Tags: Klausur
Source:
Source:
Wie kann das Suchproblem der Analyse gelöst werden?
Modellmatching: Bild segmentieren und in Modell- und Bildbestandteile zerlegen und diese matchen ...
... In dem man es als Graphproblem auffast.
Dabei wird ein Graph aufgebaut durch Zuordnungen zwischen Merkmalen des Modells und Merkmalen des aufgenommenen Bildes. Man darf nur zulassen, dass ein Merkmal (egal auf welcher Seite) eindeutig zugeteilt ist oder gar nicht zugeteilt ist. Mehrfachzuteilungen sind zu vermeiden.
Kanten können über Gewichtsfunktionen gesteuert werden.
Gute Zuordnung = hohe Werte der Gewichte Maximierungsproblem.
Maximierungsproblem.
Suchprobleme: Ungarischer Algorithmus, A*-Graphsuche, dynamische Programmierung.
... In dem man es als Graphproblem auffast.
Dabei wird ein Graph aufgebaut durch Zuordnungen zwischen Merkmalen des Modells und Merkmalen des aufgenommenen Bildes. Man darf nur zulassen, dass ein Merkmal (egal auf welcher Seite) eindeutig zugeteilt ist oder gar nicht zugeteilt ist. Mehrfachzuteilungen sind zu vermeiden.
Kanten können über Gewichtsfunktionen gesteuert werden.
Gute Zuordnung = hohe Werte der Gewichte
 Maximierungsproblem.
Maximierungsproblem.Suchprobleme: Ungarischer Algorithmus, A*-Graphsuche, dynamische Programmierung.
Tags: Klausur
Source:
Source:
Wie kann ich eine BRDF parametrisieren?
Ein Lichtfeld ist eine Form der Darstellung der BRDF.
Man nimmt Bilder mit einer Kamera auf. Man fasst einen Pixel als einen Sehstrahl zwischen Kamerabrennpunkt und diesem Punkt in der Welt auf.
Bilder mit einer Kamera auf. Man fasst einen Pixel als einen Sehstrahl zwischen Kamerabrennpunkt und diesem Punkt in der Welt auf.
Diesen Strahl kann man im 3D durch zwei Ebenen darstellen, also durch vier Koordinaten.
Man brauch viele Strahlen, diese werden alle benutzt, um zwischen ihnen zu interpolieren.
Anwendung:
Das ermöglicht uns 3D Kamera-Flüge, ohne dass auch nur ein Primitv gerendert werden musste.
Es gibt Aufsätze für DSLRs, fertige Kameras (Lytro) und Patente von Apple, um es auf Smartphones zu bringen.
Es ist auch möglich die Blende im Nachhinein zu verändern.
Es ist nach Prof. Paulus ein sehr guter Kontaktpunkt der CG und BV.
Man nimmt
 Bilder mit einer Kamera auf. Man fasst einen Pixel als einen Sehstrahl zwischen Kamerabrennpunkt und diesem Punkt in der Welt auf.
Bilder mit einer Kamera auf. Man fasst einen Pixel als einen Sehstrahl zwischen Kamerabrennpunkt und diesem Punkt in der Welt auf. Diesen Strahl kann man im 3D durch zwei Ebenen darstellen, also durch vier Koordinaten.
Man brauch viele Strahlen, diese werden alle benutzt, um zwischen ihnen zu interpolieren.
Anwendung:
- Man hat ein Lichtfeld wie oben beschrieben aufgebaut
- Es wird eine Kamera zwischen den Ebenen positioniert
- Es wird ausgerechnet, welche Sichtstrahlen diese Kamera haben würde
- Dann wird aus dem Lichtfeld die Strahlen genommen, die am besten zu den Sichtstrahlen der Kamera passen.
- Gegebenenfalls müssen Strahlen auch interpoliert werden, was aber ganz von der Auflösung des Lichtfeldes abhängt.
Das ermöglicht uns 3D Kamera-Flüge, ohne dass auch nur ein Primitv gerendert werden musste.
Es gibt Aufsätze für DSLRs, fertige Kameras (Lytro) und Patente von Apple, um es auf Smartphones zu bringen.
Es ist auch möglich die Blende im Nachhinein zu verändern.
Es ist nach Prof. Paulus ein sehr guter Kontaktpunkt der CG und BV.
Tags: Klausur
Source:
Source:
Was sind MacAdams-Ellipsen?
MacAdam sind Ellipsen von Bereichen, in denen Menschen die Farben als gleich wahrnehmen.
Die Größe variiert im Farbraum je nach ihrem Ort in diesem.
Als Beispiel wurde der XY-Farbraum mit ihren MacAdam-Ellipsen aufgetragen. Da solche überhaupt existieren, ist es der Beweis, dass Farbdifferenzen im XYZ nicht das selbe bedeuten.
Im Lab werden diese Ellipsen zu gleichgroßen Kreisen, was der Beweis ist, dass Lab den gleichen Farbabstand liefert wie die menschliche Wahrnehmung.
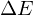 ist die Farbdifferenz des Lab.
ist die Farbdifferenz des Lab.
- Die Ellipsen werden gebildet aus der Standardabweichung.
Die Größe variiert im Farbraum je nach ihrem Ort in diesem.
Als Beispiel wurde der XY-Farbraum mit ihren MacAdam-Ellipsen aufgetragen. Da solche überhaupt existieren, ist es der Beweis, dass Farbdifferenzen im XYZ nicht das selbe bedeuten.
Im Lab werden diese Ellipsen zu gleichgroßen Kreisen, was der Beweis ist, dass Lab den gleichen Farbabstand liefert wie die menschliche Wahrnehmung.
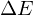 ist die Farbdifferenz des Lab.
ist die Farbdifferenz des Lab.- Die Ellipsen werden gebildet aus der Standardabweichung.
Tags: Klausur
Source:
Source:
Wie ist 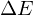 definiert?
definiert?
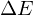 definiert?
definiert?CIELAB Farb-Metrik
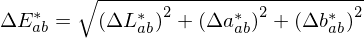
Ein Wert von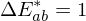 resp.
resp. 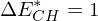 entspricht der minimal menschlich wahrnehmbaren Farbdifferenz
entspricht der minimal menschlich wahrnehmbaren Farbdifferenz  Farbmetrik durch CIE (International Commission on Illumination) verwendet den uniformen L∗a∗b ∗ Farbraum.
Farbmetrik durch CIE (International Commission on Illumination) verwendet den uniformen L∗a∗b ∗ Farbraum.
lightness-axis , red-green-axis
, red-green-axis 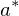 , yellow-blue-axis
, yellow-blue-axis 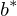
In diesem Farbraum: Euklidischer Abstand entspreicht der Wahrnehmung. Die Symoble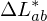 ,
, 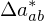 ,
, 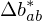 bedeuten komponentenweise Differenz zwischen zwei Lab-Farben.
bedeuten komponentenweise Differenz zwischen zwei Lab-Farben.
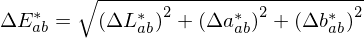
Ein Wert von
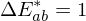 resp.
resp. 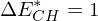 entspricht der minimal menschlich wahrnehmbaren Farbdifferenz
entspricht der minimal menschlich wahrnehmbaren Farbdifferenz 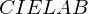 Farbmetrik durch CIE (International Commission on Illumination) verwendet den uniformen L∗a∗b ∗ Farbraum.
Farbmetrik durch CIE (International Commission on Illumination) verwendet den uniformen L∗a∗b ∗ Farbraum.lightness-axis
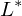 , red-green-axis
, red-green-axis 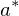 , yellow-blue-axis
, yellow-blue-axis 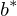
In diesem Farbraum: Euklidischer Abstand entspreicht der Wahrnehmung. Die Symoble
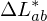 ,
, 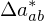 ,
, 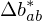 bedeuten komponentenweise Differenz zwischen zwei Lab-Farben.
bedeuten komponentenweise Differenz zwischen zwei Lab-Farben.Tags: Klausur
Source:
Source:
Wie lautet die Formel der radiometrischen Kalibrierung?
- Lampe:
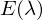
- Color Checker:

- CCD-Chip:

- Bild:

 Sensoren pro Bildpunkt, typischerweise je ein Sensor für Rot, grün un Blau, haben spektrale Empfindlichkeiten von
Sensoren pro Bildpunkt, typischerweise je ein Sensor für Rot, grün un Blau, haben spektrale Empfindlichkeiten von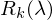 ,
, 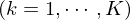
Dadurch tastet jeder Sensor
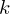 im Punkt
im Punkt 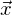 folgende Energieverteilung des Lichts ab:
folgende Energieverteilung des Lichts ab: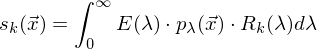
In Worten nach Prof. Paulus:
"Für einen Sensor in einem gewissen Wellenlängenbereich, an einem gewissen Ort (
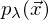 ), den ich nach draußen idealisiere mit der Beleuchtung und ihrer Reflektion und der Kameraempfindlichkeit multipliziere. Das wird integriert über den gesamten Wellenlängenbereich. "
), den ich nach draußen idealisiere mit der Beleuchtung und ihrer Reflektion und der Kameraempfindlichkeit multipliziere. Das wird integriert über den gesamten Wellenlängenbereich. "Dabei ignorieren wir die Geometrie, die Blende und die nicht Linearität, wie sie beispielsweise von der gamma Korrektur kommt.
Diskret (nach Alsam und Finlayson):
Summe von
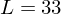 Abtastungen
Abtastungen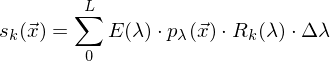
- Vector
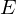 : spektrale Energie des Lichts
: spektrale Energie des Lichts - Vector
 : diskrete reflektanz an Position
: diskrete reflektanz an Position 
- Matrix
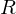 : diskrete spektrale Empfindlichkeitskurven
: diskrete spektrale Empfindlichkeitskurven
Tags: Klausur
Source:
Source:
Was ist ein inverses Problem?
Ein mathematisches Problem wird ein inverses Problem genannt, wenn man von einer beobachteten oder gewünschten Wirkung eines Systems auf die der Wirkung zugrunde liegende Ursache zurückschließen will. Inverse Probleme sind meistens sehr schwierig oder gar nicht lösbar.
Das Gegenteil eines inversen Problems ist ein direktes Problem (teilweise auch Vorwärtsproblem genannt), bei dem man ausgehend von der bekannten Ursache die Wirkung des Systems ableiten möchte.
Das Henne-Ei-Problem. Was war zuerst, das inverse oder das direkte Problem?
In der Physik und im Ingenieurwesen: Bertero and Boccacci
(1998): Eines der beiden Probleme ist grundlegender als das
andere und ist oft bereits besser untersucht; dieses Problem ist das direkte Problem.
Das Gegenteil eines inversen Problems ist ein direktes Problem (teilweise auch Vorwärtsproblem genannt), bei dem man ausgehend von der bekannten Ursache die Wirkung des Systems ableiten möchte.
Das Henne-Ei-Problem. Was war zuerst, das inverse oder das direkte Problem?
In der Physik und im Ingenieurwesen: Bertero and Boccacci
(1998): Eines der beiden Probleme ist grundlegender als das
andere und ist oft bereits besser untersucht; dieses Problem ist das direkte Problem.
Inverses vs. Direktes Problem
Inverses Problem:
Nicht genügend Information zur Lösung vorhanden.
Versuch, aus der beobachteten Wirkung eines Problems auf seine Ursache zurückzuschließen.
Direktes Problem
Alle erforderlichen Informationen zur Lösung vorhanden.
bei bekannten Ursachen, berechne die Wirkung.
Nicht genügend Information zur Lösung vorhanden.
Versuch, aus der beobachteten Wirkung eines Problems auf seine Ursache zurückzuschließen.
Direktes Problem
Alle erforderlichen Informationen zur Lösung vorhanden.
bei bekannten Ursachen, berechne die Wirkung.
Dualität der Inversen und Vorwärtsproblems
Ein Vorwärtsproblem und ein inverses Problem sind dual in dem
Sinn, als das eine in das andere überführt werden kann, indem die Rolle von Daten und Unbekannten vertauscht werden. Die Daten des einen Problems sind die Unbekannten des anderen, und umgekehrt.
Sinn, als das eine in das andere überführt werden kann, indem die Rolle von Daten und Unbekannten vertauscht werden. Die Daten des einen Problems sind die Unbekannten des anderen, und umgekehrt.
Was sind Stoerquellen und welche sind einfach behebar?
- Blooming
- Dunkelstrom (Normalverteilt)
- Photonenrauschen (Poisson-verteilt)
- Quantisierungsrauschen
Behebbares Rauschen sind:
- Photenrauschen
(Es ist multiplikativ und ist nicht einfach zu beheben) und
- Dunkelstrom
(Es ist additiv und ist einfach zu beheben
 zeitlicher Gauss)
zeitlicher Gauss)Was ist Quantisierungsrauschen?
Bei der Quantisierung eines analogen Signals entsteht ein stufenförmiges Signal, dessen Stufenzahl von der Anzahl an Abtastungen abhängt.
Es ist die Differenz zwischen dem kontinuierlichem und quantisiertem Wert.
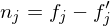
Quantisierungsrauschen:
Das Signal wird abgetastet und Informationen gehen verloren, die fehlende Information kann als Rauschen auftreten.
Das Quantisierungsrauschen ist abhängig von der Abtastrate und der Digitalisierung. Bei hoher Abtastrate und einer Digitalisierung mit hoher Auflösung ist das Quantisierungsrauschen geringer als bei niedriger Abtastrate und geringer Digitalisierung. Das zeigt sich auch im Signal-Rausch-Verhältnis (SNR). Als Annäherung gilt: Eine um 1 Bit höhere Auflösung reduziert das Quantisierungsrauschen um über 6 dB. Das Quantisierungsrauschen ist in gewisser Weise Signal-abhängig. Ist nämlich kein Signal vorhanden, dann sind keine Quantisierungsfehler und ebenso kein Quantisierungsrauschen vorhanden.
Es ist die Differenz zwischen dem kontinuierlichem und quantisiertem Wert.
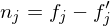
Quantisierungsrauschen:
Das Signal wird abgetastet und Informationen gehen verloren, die fehlende Information kann als Rauschen auftreten.
Das Quantisierungsrauschen ist abhängig von der Abtastrate und der Digitalisierung. Bei hoher Abtastrate und einer Digitalisierung mit hoher Auflösung ist das Quantisierungsrauschen geringer als bei niedriger Abtastrate und geringer Digitalisierung. Das zeigt sich auch im Signal-Rausch-Verhältnis (SNR). Als Annäherung gilt: Eine um 1 Bit höhere Auflösung reduziert das Quantisierungsrauschen um über 6 dB. Das Quantisierungsrauschen ist in gewisser Weise Signal-abhängig. Ist nämlich kein Signal vorhanden, dann sind keine Quantisierungsfehler und ebenso kein Quantisierungsrauschen vorhanden.
In welchem Zusammenhang steht die Aufloesung und das Signal-Rausch-Verhaeltnis (SNR)?
Das Signal-Rausch-Verhältnis (SNR) wird verbessert, desto hoeher aufgeloest wird.
Als Annäherung gilt: Eine um 1 Bit höhere Auflösung reduziert das Quantisierungsrauschen um über 6 dB.
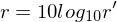
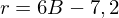
Als Annäherung gilt: Eine um 1 Bit höhere Auflösung reduziert das Quantisierungsrauschen um über 6 dB.
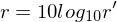
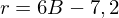
Tags: Klausur
Source:
Source:
Wozu und wie werden Quantisierungskennlinien gemacht?
Es wird nicht mehr linear quantisiert.
stattdessen wird eine optimale Quatisierung gesucht,
damit eien Funktion moeglichst gut abgebildet (quantisiert wird).
Es gitb kontinuierliche Werte, die durch Intervalle quantisiert werden.
Die Frage ist: Wie koennen diese Intervalle optimal gewaehlt werden?
Formel fuer den Fehlermass:
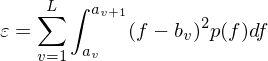
Wobei
Bsp. HDR-Bilder:
stattdessen wird eine optimale Quatisierung gesucht,
damit eien Funktion moeglichst gut abgebildet (quantisiert wird).
Es gitb kontinuierliche Werte, die durch Intervalle quantisiert werden.
Die Frage ist: Wie koennen diese Intervalle optimal gewaehlt werden?
Formel fuer den Fehlermass:
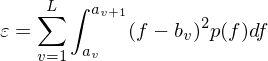
Wobei
-
 den Wert im Signal
den Wert im Signal -
 der quantisierte Wert
der quantisierte Wert -
 die Haeufigkeit, dass dieser Wert ueberhaupt auftritt
die Haeufigkeit, dass dieser Wert ueberhaupt auftritt
Bsp. HDR-Bilder:
Wie ist eine reale Kamera modelliert?
- Der Hauptpunkt
 liegt nicht im Bildzentrum
liegt nicht im Bildzentrum - Rotationsmatrix
- Translationsvektor
- intrinsische und extrinsische Kameraparameter werden getrennt
- Kamera-Matrix (
 )
) - Pose-Matrix (
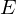 )
) -
 : Hauptpunkt
: Hauptpunkt -
 : Kamerakonstante
: Kamerakonstante 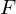
-
 : Massstabsunterschied s der Achsen und Scherung der Achsen
: Massstabsunterschied s der Achsen und Scherung der Achsen 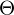
Was ist Kalibrierung?
- Waehle Modell fuer Sensor
- Suche mathematische Beschreibung, inkl. einer Parametermenge
- W aehle Kalibrierobjekt mit gut erkennbaren Merkmalen
- Miss die Merkmale
- Bildaufnahme des Kalibrierobjekts
- Gleichungssystem aufstellen
- Loese Gleichungssystem auf nach unbekannen Parametern
Tags: Klausur
Source:
Source:
Tags: Klausur
Source:
Source:
Welche Stoerquellen gibt es?
Es existieren Stoerquellen bei der
Chromatische Aberration:
Die chromatische Aberration ist ein Abbildungsfehler optischer Linsen, der dadurch entsteht, dass Licht unterschiedlicher Wellenlänge oder Farbe verschieden stark gebrochen wird.
Schaubild
- Uebertragung
- Elektronik
- Optik Verzerrung Chromatische Aberration
Chromatische Aberration:
Die chromatische Aberration ist ein Abbildungsfehler optischer Linsen, der dadurch entsteht, dass Licht unterschiedlicher Wellenlänge oder Farbe verschieden stark gebrochen wird.
Schaubild
Was sind die 4 U's?
Bildanalyse miss zurechtkommen mit:
Unsicherheit:
Ungenauigkeit:
Unwissenheit:
Unvollstaendigkeit:
- Unsicherheit
- Ungenauigkeit
- Unwissenheit
- Unvollstaendigkeit
Unsicherheit:
- Wir haben unsicheres Wissen ueber die Welt
Ungenauigkeit:
- Wir haben ungenaue Sensoren
Unwissenheit:
- Wir haben eine Unwissenheit ueber das, was wir ueberhaupt sehen
Unvollstaendigkeit:
- In der Regel haben wir unvollstaendige Daten, selbst mit genuegend Sensorinformationen, reicht das Wissen nicht aus
Wie erfolgt die Reizverarbeitung in der Netzhaut?
Man geht davon aus, dass eine gewisse Vorverarbeitung im Auge auf Basis der Photorezeptoren stattfindet. Denn es gehen weniger Nerven aus dem Auge, als es Photorezeptoren gibt.
Es gibt auf der Retina 4 verschiedene Typen von Rezeptoren:
Auf Neuronenbasis wird nach der Zonentheorie aus alle Zapfen und den Staebchen die Helligkeit bestimmt.
Das Gegenfarbsignal Blau-Gelb und
das Gegenfarbsignal Rot-Gruen
Es gibt auf der Retina 4 verschiedene Typen von Rezeptoren:
- L Zapfen (Farbe rot)
- M Zapfen (Farbe gruen)
- S Zapfen (Farbe blau)
- Staebchen (Helligkeit)
Auf Neuronenbasis wird nach der Zonentheorie aus alle Zapfen und den Staebchen die Helligkeit bestimmt.
Das Gegenfarbsignal Blau-Gelb und
das Gegenfarbsignal Rot-Gruen
Was fuer eine Rolle spielen Licht und Farbe in Hinblick auf CV
Hier geht es speziell um Folie 39 (2.2-4)
Dort ist ein Graph mit gerichteten Kanten abgebildet.
Es sind zwei Kreise zu erkennen, die aber auch ineinander
uebergehen, wie eine Acht aufgebaut.
Auf der rechten Seite, dieser liegenden Acht, ist das Wahrnehmen durch den Menschen abgebildet. Einerseits der realen Welt und andererseits eines aufbereiteten Mediums
Der linke Teil des Graphen beschreibt die Wahrnehmung und Analyse durch den Computer.
Der Computer bestitzt ein Modell, das die Welt abbildet. Dieses Modell kann instanziiert werden zu einer Beschreibung. Anhand dieser Beschreibung kann ein Bild synthetisiert (Graphik) werden, aber auch ein beliebiges Bild analysiert werden.
Dort ist ein Graph mit gerichteten Kanten abgebildet.
Es sind zwei Kreise zu erkennen, die aber auch ineinander
uebergehen, wie eine Acht aufgebaut.
Auf der rechten Seite, dieser liegenden Acht, ist das Wahrnehmen durch den Menschen abgebildet. Einerseits der realen Welt und andererseits eines aufbereiteten Mediums
Der linke Teil des Graphen beschreibt die Wahrnehmung und Analyse durch den Computer.
Der Computer bestitzt ein Modell, das die Welt abbildet. Dieses Modell kann instanziiert werden zu einer Beschreibung. Anhand dieser Beschreibung kann ein Bild synthetisiert (Graphik) werden, aber auch ein beliebiges Bild analysiert werden.
Was ist die Photogrammetrie
Photogrammetrie und Fernerkundung dienen zur beruehrungslosen Erfassung und Vermessung von Objekten mit Hilfe von Bildern. Die frueher eigenstaendigen Gebiete "Photogrammetrie" mit Schwerpunkt auf geometrischen Fragen und "Fernerkundung", die sich vor allem mit der Bildinterpretation befasst, wachsen heute immer mehr zusammen.
Wo von haengt die Aufloesung einer Kamera massgeblich von ab?
Die Beugung an der Blende fuehrt dazu, dass die Aufloesung nicht beliebig hochgedreht werden kann.
Es gibt ein Zusammenhang mit der Oeffnung.
Man kann den Sensor zwar beliebig hoch aufloesen,
aber wenn die Blende nicht angepasst wird, gewinnt man nichts an der Aufloesung.
Weil die Beugung dazu fuehrt, dass Punkte, auf Kurven abgebildet werden (Besselfunktionen). Dadurch entstehen Nebenmaxima, die, sich mit dem eigentlich angesprochenen Pixel ueberlagern.
Durch die Beugung der Linse werden zwei Punkte auf der Bildflaeche ueberlagert. Man kann sie also nicht unterscheiden.
Man kann sie also nicht unterscheiden.
In der Klausur kann es gut sein, dass ein Bild gemalt werden soll.
Es gibt ein Zusammenhang mit der Oeffnung.
Man kann den Sensor zwar beliebig hoch aufloesen,
aber wenn die Blende nicht angepasst wird, gewinnt man nichts an der Aufloesung.
Weil die Beugung dazu fuehrt, dass Punkte, auf Kurven abgebildet werden (Besselfunktionen). Dadurch entstehen Nebenmaxima, die, sich mit dem eigentlich angesprochenen Pixel ueberlagern.
Durch die Beugung der Linse werden zwei Punkte auf der Bildflaeche ueberlagert.
 Man kann sie also nicht unterscheiden.
Man kann sie also nicht unterscheiden.In der Klausur kann es gut sein, dass ein Bild gemalt werden soll.
Wie erfolgt die Codierung?
Die Codierung erfolgt, indem man
Schaubild:
Aufnahme des Musters Vorfilterung
Vorfilterung  Abtastung
Abtastung  Codierung
Codierung  Speicherung, Uebertragung, Verarbeitung
Speicherung, Uebertragung, Verarbeitung  Decodierung
Decodierung  Nachfilterung
Nachfilterung  Wiedergabe des Musters
Wiedergabe des Musters
- die Amplituden (oder Funktionswerte) an endlich vielen, (hier: aequidistanten) stuetzstellen misst: Abtastung
- die Funktionswerte mit endlich vielen ganzzahligen Werten darstellt: Quantisierung
Schaubild:
Aufnahme des Musters
 Vorfilterung
Vorfilterung  Abtastung
Abtastung  Codierung
Codierung  Speicherung, Uebertragung, Verarbeitung
Speicherung, Uebertragung, Verarbeitung  Decodierung
Decodierung  Nachfilterung
Nachfilterung  Wiedergabe des Musters
Wiedergabe des MustersWas besagt das Abtasttheorem?
Ist ein Spektrum Bandbegrenzt, dann gilt das Abtasttheorem.
Das besagt, dass wenn man mit der doppelten Grenzfrequenz abtastet, interpoliert werden kann, mit einer unendlichen Summe ueber den Fourierkoeffizienten, um daraus eine vollstaendige Rekonstruktion des Originals wieder hergestellt werden kann.
Das besagt, dass wenn man mit der doppelten Grenzfrequenz abtastet, interpoliert werden kann, mit einer unendlichen Summe ueber den Fourierkoeffizienten, um daraus eine vollstaendige Rekonstruktion des Originals wieder hergestellt werden kann.
Wo steckt der Fehler Rekonstruktion?
Das Abtasttheorem arbeitet mit einer unendlichen Summe ueber den Fourierkoeffizienten, um daraus eine vollstaendige Rekonstruktion des Originals herzustellen.
1. Da wir nicht ueber eine unendliche Summe laufen koennen, wird ein Fehler in der Rekonstruktion gemacht.
2. Die abgetasteten Werte sind diskretisiert und dann quantisiert, was ebenfalls einen Quantisierungsfehler liefert.
1. Da wir nicht ueber eine unendliche Summe laufen koennen, wird ein Fehler in der Rekonstruktion gemacht.
2. Die abgetasteten Werte sind diskretisiert und dann quantisiert, was ebenfalls einen Quantisierungsfehler liefert.
Unterschied CMOS vs. CCD
| CCD | CMOS | |
| akkumulation von Ladung | kein Uebersprechen | |
| Strahteilung mittels Prisma (teuer, anfaelliger, hoehere aufloesung) oder Filter (billig, aber geringe aufloesung) | geringerer Stromverbrauch als CCD | |
| Bayer-Pattern | Fuellfaktor ca. 50% | |
| Dunkelstrom! | Verstaerker ist nah am Sensor | |
| Uebersprehchen! (Blooming) |
Was ist der Dunkelstrom?
Der Dunkelstrom ist Normalverteilt und ist bezeichnet als die spontane Bildung von freien Ladungsträgern durch Wärme in einem lichtempfindlichen Halbleiter, beispielsweise einem CCD-Bildsensor.
Systematisches durch den Dunkelstrom verursachtes Rauschen auf digitalen Bildern kann zum Teil nachträglich durch Bildbearbeitung am Computer oder bereits in der Kamera entfernt werden.
Systematisches durch den Dunkelstrom verursachtes Rauschen auf digitalen Bildern kann zum Teil nachträglich durch Bildbearbeitung am Computer oder bereits in der Kamera entfernt werden.
Was ist der H-Sync / V-Sync
- Der H-Sync (end of line) ist ein Synchronisierungssignal, dass das Ende einer Bildzeile angibt. Gibt es 575, es sind aber nur 485 sichtbar. Der Rest ist fuer Zusatzinformationen reserviert, beispielsweise auch dem Videotext (TV).
- Der V-Sync (end of field) ist ein Synchronisierungssignal, dass das Ende des Bildes angibt. Gibt es etwa ueber 50
Was ist Interlace und wodurch kann es reduziert werden?
Als Interlace oder Interlacing wird ein Speicherverfahren für Rastergrafiken bezeichnet. In unserem Beispiel wird das Bild in zwei Teile zerlegt. Erst werden die geraden Zeilen uebertragen, danach die ungeraden. Dadurch kommt es zu horizontalen verschiebungen der geraden zu den ungeraden Bildzeilen.
Es kann reduziert werden, durch
GIF zur Veranschaulichung
Es kann reduziert werden, durch
- Verwendung nur eines Halbbildes
- Tiefpassfilterung und Unterabtastung
GIF zur Veranschaulichung
Was bezeichnet Prof. Mueller mit dem "Quietscheentchenproblem"?
Es ist das Problem, dass, bspw. ein Qietscheentchen, nicht so aufgenommen und auf einem Monitor dargestellt werden kann, dass der gleiche Farbeindruck in beiden Abbildungen, also Original und auf dem Monitor, entsteht.
Hierunter werden auch "Bilder, denen wir vertrauen koennen" verstanden, wenn die Abbildungen gleich sind.
Hierunter werden auch "Bilder, denen wir vertrauen koennen" verstanden, wenn die Abbildungen gleich sind.
Wie funktioniert die Koord. Transformation
Sie wird mithilfe des Skalarproduktes realisiert.
Beispielsweise wollen wir einen Punkt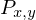 in das Koordinatensystem u,v, welches in Weltkoordinatensysteme gegeben ist, bringen.
in das Koordinatensystem u,v, welches in Weltkoordinatensysteme gegeben ist, bringen.
UV-System:
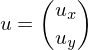 und
und 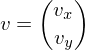
Gesucht ist:
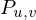
Gegeben ist:
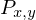
Loesung
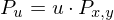 und
und 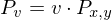
Das kann auch mit hilfe einer Matrix in einem gemacht werden.
Martrix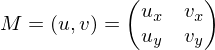
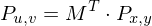
Und das Tolle ist, der andere Weg ist einfach die nicht transponierte:
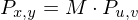
Warum, das wie transponiert werden muss kann man sich mit der Transformationsregel von Prof. Mueller verdeutlichen:
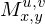
Da hochgestellter index der -Matrix ungleich der Basis von
-Matrix ungleich der Basis von 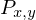 ist, muss
ist, muss  transponiert werden.
transponiert werden.
Beispielsweise wollen wir einen Punkt
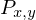 in das Koordinatensystem u,v, welches in Weltkoordinatensysteme gegeben ist, bringen.
in das Koordinatensystem u,v, welches in Weltkoordinatensysteme gegeben ist, bringen.UV-System:
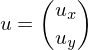 und
und 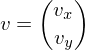
Gesucht ist:
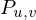
Gegeben ist:
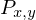
Loesung
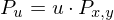 und
und 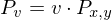
Das kann auch mit hilfe einer Matrix in einem gemacht werden.
Martrix
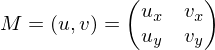
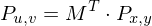
Und das Tolle ist, der andere Weg ist einfach die nicht transponierte:
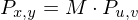
Warum, das wie transponiert werden muss kann man sich mit der Transformationsregel von Prof. Mueller verdeutlichen:
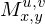
Da hochgestellter index der
 -Matrix ungleich der Basis von
-Matrix ungleich der Basis von 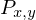 ist, muss
ist, muss  transponiert werden.
transponiert werden.Wie kann man die Flaeche unter einer Kurve bestimmen?
Mit dem Skalarprodukt!
Beispielsweise hat man zwei Spektren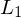 und
und 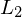 .
.
Das Skalar von ihnen ist die Flaeche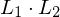 .
.
Ausfuehrlich ist es das Integral der beiden Funktionen miteinander multipliziert:
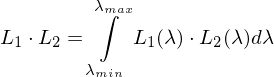
Im diskreten Fall heisst das bei uns:
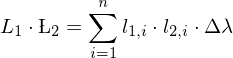
Die Multiplikation mit der Schrittweite (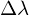 ) ist sehr wichtig.
) ist sehr wichtig.
Beispielsweise hat man zwei Spektren
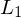 und
und 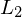 .
.Das Skalar von ihnen ist die Flaeche
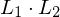 .
.Ausfuehrlich ist es das Integral der beiden Funktionen miteinander multipliziert:
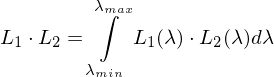
Im diskreten Fall heisst das bei uns:
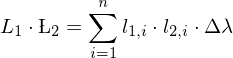
Die Multiplikation mit der Schrittweite (
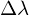 ) ist sehr wichtig.
) ist sehr wichtig.Was ist der Normfarbraum?
wikipedia:
"CIE-Normfarbsystem wurde von der Internationalen Beleuchtungskommission (CIE – Commission internationale de l’éclairage) definiert, um eine Relation zwischen der menschlichen Farbwahrnehmung (Farbe) und den physikalischen Ursachen des Farbreizes (Farbvalenz) herzustellen."
Zumeist notiert als:
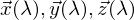
Bei Prof. Mueller:
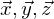
"CIE-Normfarbsystem wurde von der Internationalen Beleuchtungskommission (CIE – Commission internationale de l’éclairage) definiert, um eine Relation zwischen der menschlichen Farbwahrnehmung (Farbe) und den physikalischen Ursachen des Farbreizes (Farbvalenz) herzustellen."
Zumeist notiert als:
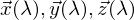
Bei Prof. Mueller:
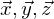
Was beschreibt die Basistransformation?
Der CIE-Normfarbraum ist definiert durch 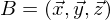 . Das ist die Basis.
. Das ist die Basis.
Jede Linearkombination der Basisvektoren mit reellen Zahlen liefert wieder eine Basis dieses Farbraums, insfern die neuen Basisvektoren linear unabhaengig sind.
--> Das kann erreicht werden in dem wir mit einer nicht-singulaeren, linearen 3x3 Matrix multiplizieren.
multiplizieren.
Jede Basis liefert ein eigenes Koordinatensystem, wobei der gleiche Vektroraum aufgespannt wird (die lineare Hueller ist identisch)
Es veraendern sich aber Koordinaten bei der Ueberfuehrung.
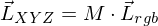
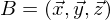 . Das ist die Basis.
. Das ist die Basis.Jede Linearkombination der Basisvektoren mit reellen Zahlen liefert wieder eine Basis dieses Farbraums, insfern die neuen Basisvektoren linear unabhaengig sind.
--> Das kann erreicht werden in dem wir mit einer nicht-singulaeren, linearen 3x3 Matrix
 multiplizieren.
multiplizieren.Jede Basis liefert ein eigenes Koordinatensystem, wobei der gleiche Vektroraum aufgespannt wird (die lineare Hueller ist identisch)
Es veraendern sich aber Koordinaten bei der Ueberfuehrung.
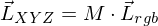
Reicht der 3D Farbraum uns aus?
Nein.
Im Kontext eines 3-dimensionalen Farbraums geht es
vorrangig um einen konsistenten Farbeindruck für einen
menschlichen Betrachter.
Den n-dimensionalen Spektralraum benötigen wir, um
spektrale Funktionen möglichst gut zu approximieren.
Der 3D Farbraum reicht nicht aus, trotzdem bauen alle Renderingmethoden (inkl. der GPU selbst) darauf auf.
Im Kontext eines 3-dimensionalen Farbraums geht es
vorrangig um einen konsistenten Farbeindruck für einen
menschlichen Betrachter.
Den n-dimensionalen Spektralraum benötigen wir, um
spektrale Funktionen möglichst gut zu approximieren.
Der 3D Farbraum reicht nicht aus, trotzdem bauen alle Renderingmethoden (inkl. der GPU selbst) darauf auf.
Rueckfuehrung eines XYZ-Wertes in ein Spektrum. ist 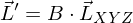 richtig?
richtig?
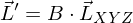 richtig?
richtig?Es ist zwar die logische Linearkombination aus dem umgekehrten Weg, um aus einem Spektrum einen XYZ-Wert zu machen.
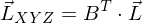
Aber nein. Es ist leider falsch.
Waere die Loesung gueltig, wuerde eine erneute Projektion wieder die urspruengliche XZY-Werte liefern. Macht sie aber nicht.
Das laesst sich nur mit orthonormalen Basen erreichen.
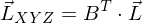
Aber nein. Es ist leider falsch.
Waere die Loesung gueltig, wuerde eine erneute Projektion wieder die urspruengliche XZY-Werte liefern. Macht sie aber nicht.
Das laesst sich nur mit orthonormalen Basen erreichen.
Was beschreibt die duale Basis?
Im Allgemeinen Fall brauchen wir zwei Sätze von
Basisfunktionen (duale Basis).
- Eine Projektions- oder Konstruktionbasis
- Eine Rekonstruktionsbasis
Beispiel:
Kamera und ein Display
Mit Hilfe der Kamera (Sensorantwortkurve) transformieren wir
ein eingehendes Spektrum auf den rgb-Wert eines Pixels.
Mit Hilfe des Displays (Spektren der Pixel, sog. Primaries)
rekonstruieren wir aus rgb wieder ein Spektrum.
Basisfunktionen (duale Basis).
- Eine Projektions- oder Konstruktionbasis
- Eine Rekonstruktionsbasis
Beispiel:
Kamera und ein Display
Mit Hilfe der Kamera (Sensorantwortkurve) transformieren wir
ein eingehendes Spektrum auf den rgb-Wert eines Pixels.
Mit Hilfe des Displays (Spektren der Pixel, sog. Primaries)
rekonstruieren wir aus rgb wieder ein Spektrum.
Was ist die Rekonstruktionsbasis?
Beispiel Display:
Mit Hilfe des Displays (Spektren der Pixel, sog. Primaries) rekonstruieren wir aus rgb wieder ein Spektrum.
Display leuchtet mit Primaries: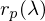 ,
, 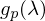 ,
, 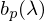 =
= 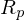
Die Rekonstruktionsbasis wird durch ein p wie „primaries“ gekennzeichnet)
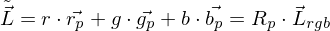
Wobei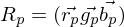 gilt.
gilt.
Aber:
Das rekonstruierte Spektrum ist i. d. Regel vom Originalspektrum verschieden:
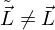
Mit Hilfe des Displays (Spektren der Pixel, sog. Primaries) rekonstruieren wir aus rgb wieder ein Spektrum.
Display leuchtet mit Primaries:
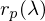 ,
, 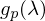 ,
, 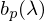 =
= 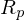
Die Rekonstruktionsbasis wird durch ein p wie „primaries“ gekennzeichnet)
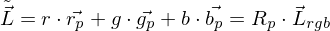
Wobei
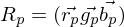 gilt.
gilt.Aber:
Das rekonstruierte Spektrum ist i. d. Regel vom Originalspektrum verschieden:
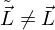
Wie bildet sich die Einheitsmatrix 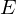 ?
?
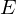 ?
?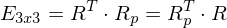
Im Kontext der Farbe haben wir aber nx3 Matrizen, wobei n die Anzahl der Samples ist, mit der das Spektrum diskretisiert wurde.
Aber
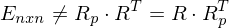
-- > Das Produkt nennt man Cohen Matrix und wird mit
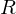 abgekuerzt. Sie wird benutzt, um fundementale Metamere beliebiger Spektren zu erzeugen.
abgekuerzt. Sie wird benutzt, um fundementale Metamere beliebiger Spektren zu erzeugen.Was ist ein identischer Farbeindruck und wie ist er formalisiert?
Wir sprechen von einem identischen Farbeindruck (color match), wenn für zwei verschiedene Spektren 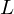 und
und 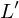 gilt
gilt
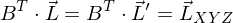
wobei die CIE XYZ Color Matching Funktionen (Normspektralwertkurven) sind.
die CIE XYZ Color Matching Funktionen (Normspektralwertkurven) sind.
Haben 2 Spektren die gleichen XYZ- Koordinaten, dann liefern sie für einen „Normalbeobachter“ auch einen identischen Farbeindruck.
Spektren mit identischem Farbeindruck nennen wir Metamere
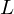 und
und 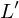 gilt
gilt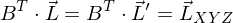
wobei
 die CIE XYZ Color Matching Funktionen (Normspektralwertkurven) sind.
die CIE XYZ Color Matching Funktionen (Normspektralwertkurven) sind.Haben 2 Spektren die gleichen XYZ- Koordinaten, dann liefern sie für einen „Normalbeobachter“ auch einen identischen Farbeindruck.
Spektren mit identischem Farbeindruck nennen wir Metamere
Wie sehen die CIE: Konstruktions- und Rekonstruktionsbasis
aus?
aus?
Leider nur links, da es sonst Geld auf dieser Plattform hier kostet:
 Also Konstruktionsbasis
Also Konstruktionsbasis
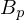 Also Rekonstruktionsbasis. Aehnlich wie
Also Rekonstruktionsbasis. Aehnlich wie  , nur mit den negativen auswuechsen (noch kein passendes bild gefunden)
, nur mit den negativen auswuechsen (noch kein passendes bild gefunden)
 Also Konstruktionsbasis
Also Konstruktionsbasis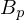 Also Rekonstruktionsbasis. Aehnlich wie
Also Rekonstruktionsbasis. Aehnlich wie  , nur mit den negativen auswuechsen (noch kein passendes bild gefunden)
, nur mit den negativen auswuechsen (noch kein passendes bild gefunden)Beschreiben Sie die 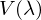 -Kurve
-Kurve
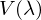 -Kurve
-KurveV-Lambda-Kurve auf Wikipedia

- beschreibt den spektralen Hellempfindlichkeitsgrad für Tagessehen
- ca. 550nm (grün-gelb) nimmt man am hellsten wahr

- beschreibt den spektralen Hellempfindlichkeitsgrad für Tagessehen
- ca. 550nm (grün-gelb) nimmt man am hellsten wahr
Nenne die Kerngroessen der Photometrie
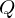 | Lichtmenge |  |  | Gesamten ausgesendeten Photonen |
 | Strahlungsmenge | 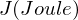 | Für eine Wellenlänge ausgendete Photonen | |
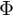 | Lichtstrom |  |  | Gesamten ausgesendeten Photonen pro Zeiteinheit |
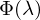 | Strahlungsfluss |  | Für eine Wellenlänge ausgesendete Photonen pro Zeiteinheit | |
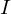 | Lichststaerke |  | 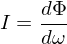 | Gesamten ausgesendeten Photonen pro Zeiteinheit und Raumwinkel |
 | Strahlstärke |  | Für eine Wellenlänge ausgesendeten Photonen pro Zeiteinheit und Raumwinkel | |
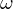 | Raumwinkel | 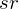 |  | Verhältnis der bedeckten Kugeloberfläche 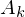 zum Quadrat des Kugelradius zum Quadrat des Kugelradius  |
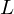 | Leuchtdichte |  |  | Ist die wahrgenommene Helligkeit unter Beachtung des Betrachtungswinkels |
 | Spez. Lichtausstrahlung |  | ||
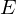 | Beleuchtungsstaerke |  Lux) Lux) |  | Ist der auftreffende Strahlungsfluss pro Flaechenelement. |
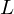 | Strahldichte |  |  | Das, was das Auge "sieht" |
Was ist der Lambert-Strahler?
Der Lambert-Strahler zeichnet sich dadurch aus, dass
seine Leuchtdichte unter jedem Betrachtungswinkel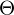 konstant ist und er dadurch von jeder Blickrichtung
konstant ist und er dadurch von jeder Blickrichtung
gleich hell erscheint.
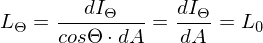
Wobei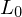 die Leuchtdichte bei
die Leuchtdichte bei 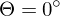 ist, also so, als wuerde man direkt in die Lichtquelle hineinschauen.
ist, also so, als wuerde man direkt in die Lichtquelle hineinschauen.
seine Leuchtdichte unter jedem Betrachtungswinkel
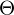 konstant ist und er dadurch von jeder Blickrichtung
konstant ist und er dadurch von jeder Blickrichtunggleich hell erscheint.
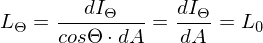
Wobei
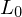 die Leuchtdichte bei
die Leuchtdichte bei 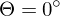 ist, also so, als wuerde man direkt in die Lichtquelle hineinschauen.
ist, also so, als wuerde man direkt in die Lichtquelle hineinschauen.Invarianz der Leuchtdichte. Was ist das?
Die Leuchtdichte bleibt in Richtung eine Lichtstrahls konstant.
Dies gilt auch im Zusammenhang mit optischen Abbildungen (Voraussetzung: keine Verluste durch Absorption oder Streuung)
Auf dieser Invarianz baut das Prinzip des Ray Tracings, des Renderings und der bisherigen Betrachtung der Beleuchtungsmodelle auf.
Dies gilt auch im Zusammenhang mit optischen Abbildungen (Voraussetzung: keine Verluste durch Absorption oder Streuung)
Auf dieser Invarianz baut das Prinzip des Ray Tracings, des Renderings und der bisherigen Betrachtung der Beleuchtungsmodelle auf.
Was ist eine LVK?
- Lichtverteilungskurve
- gibt die Abstrahlcharakteristik einer Leuchte an
- normalerweise müsste sie für jede Wellenlänge extra angegeben werden; oft wird aber nur das Spektrum für eine Lichtquelle angegeben
- bei isotropen Materialien (rotationssymmetrisch) ist die LVK nur abhängig von einem Winkel
- bei anisotropen Materialien ist die LVK abhängig von zwei Austrittswinkeln
- gibt die Abstrahlcharakteristik einer Leuchte an
- normalerweise müsste sie für jede Wellenlänge extra angegeben werden; oft wird aber nur das Spektrum für eine Lichtquelle angegeben
- bei isotropen Materialien (rotationssymmetrisch) ist die LVK nur abhängig von einem Winkel
- bei anisotropen Materialien ist die LVK abhängig von zwei Austrittswinkeln
Was ist eine Duale Basis und was die Cohen Matrix?
- 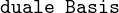 ist in unserem Zusammenhang eine Bediungung, um eine farbkonsistente Abbildung zu ermöglichen. Ein durch einen XYZ-Wert rekonstruiertes Spektrum wird nach der Projektion auf die BAsis wieder auf den XYZ-Wert abgebildet.
ist in unserem Zusammenhang eine Bediungung, um eine farbkonsistente Abbildung zu ermöglichen. Ein durch einen XYZ-Wert rekonstruiertes Spektrum wird nach der Projektion auf die BAsis wieder auf den XYZ-Wert abgebildet.
Es ergibt sich, dass
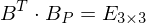 mit
mit 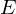 als
als 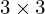 Einheitsmatrix
Einheitsmatrix
- mithilfe der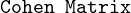 berechnet man fundamentale Metamere beliebiger Spektren in der CIE-Normbasis.
berechnet man fundamentale Metamere beliebiger Spektren in der CIE-Normbasis.
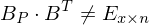 als Cohen-Matrix folgt aus:
als Cohen-Matrix folgt aus:
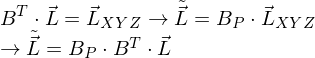
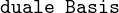 ist in unserem Zusammenhang eine Bediungung, um eine farbkonsistente Abbildung zu ermöglichen. Ein durch einen XYZ-Wert rekonstruiertes Spektrum wird nach der Projektion auf die BAsis wieder auf den XYZ-Wert abgebildet.
ist in unserem Zusammenhang eine Bediungung, um eine farbkonsistente Abbildung zu ermöglichen. Ein durch einen XYZ-Wert rekonstruiertes Spektrum wird nach der Projektion auf die BAsis wieder auf den XYZ-Wert abgebildet.Es ergibt sich, dass
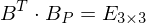 mit
mit 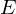 als
als 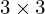 Einheitsmatrix
Einheitsmatrix- mithilfe der
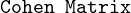 berechnet man fundamentale Metamere beliebiger Spektren in der CIE-Normbasis.
berechnet man fundamentale Metamere beliebiger Spektren in der CIE-Normbasis.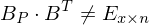 als Cohen-Matrix folgt aus:
als Cohen-Matrix folgt aus: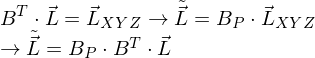
Welche Eigenschaft besitzt das Differenzspektrum?
Und was passiert, wenn man nun ein Spektrum auf die CIE-Normbsis projiziert?
Und was passiert, wenn man nun ein Spektrum auf die CIE-Normbsis projiziert?
Sein Farbeindruck ist immer schwarz (metameric black), deshalb wird es auch Schwarz-Metamer genannt. Es liegt vollständig im Nullraum und trägt nicht zum Farbeindruck bei.
Projiziert man ein Spektrum auf die CIE-Normbasis, so ergibt sich:
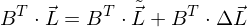
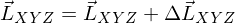
Projiziert man ein Spektrum auf die CIE-Normbasis, so ergibt sich:
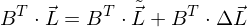
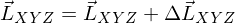
Wie lautet nun die neue Definition für Metamere? Und wie lassen sie sich mathematisch erzeugen?
bisher: Spektren mit identischem Farbeindruck sind Metamere
neu: wenn man zu einem Spektrum ein beliebiges Spektrum aus dem Null raum addiert, ist das ein Metamer
Um sie zu erzeugen, wählt man ein beliebiges Spektrum, berehcnet mithilfe der Cohen-Matrix seinen fundamentalen Metamer, und mithilfe der Differenz zum Originalspektrum seinen Schwarz-Metamer. Durch die Addition des Schwarz-Metamers zu dem fundamentalen Metamer erzeugt man für das Originalspektrum so ein gültiges Metamer
neu: wenn man zu einem Spektrum ein beliebiges Spektrum aus dem Null raum addiert, ist das ein Metamer
Um sie zu erzeugen, wählt man ein beliebiges Spektrum, berehcnet mithilfe der Cohen-Matrix seinen fundamentalen Metamer, und mithilfe der Differenz zum Originalspektrum seinen Schwarz-Metamer. Durch die Addition des Schwarz-Metamers zu dem fundamentalen Metamer erzeugt man für das Originalspektrum so ein gültiges Metamer
Welches Problem beinhalten die Schwarz-Metamere?
Eigentlich haben die Differenzspektren den Farbeindruck Null, d.h. schwarz.
Bei der Multiplikation haben sie aber eine wichtige Bedeutung, denn das Produkt von Differenzspektren ist nicht mehr schwarz.
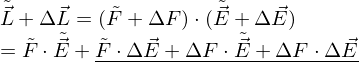
mit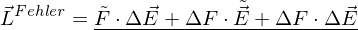
Das bedeutet, dass die Multiplikation dieser Spektren leider nicht genügt, da man den hohen Fehleranteil beachten muss. Daraus folgt:
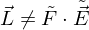
Bei der Multiplikation haben sie aber eine wichtige Bedeutung, denn das Produkt von Differenzspektren ist nicht mehr schwarz.
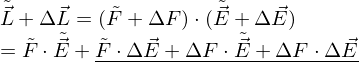
mit
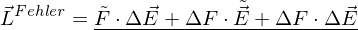
Das bedeutet, dass die Multiplikation dieser Spektren leider nicht genügt, da man den hohen Fehleranteil beachten muss. Daraus folgt:
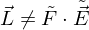
Was ist, wenn die Sensorkurven nicht die Luther-Ives-Bedingung erfüllen?
Dann kann man sie wieder zerlegen:
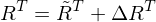
Die Projektion eines Spektrums in diese Basis liefert einen systematischen Farbfehler (Bias) und einen rgb-Wert, den man mit einer Matrix in die Koordinaten des Normfarbraums überführen kann.
Matrix in die Koordinaten des Normfarbraums überführen kann.
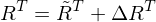
Die Projektion eines Spektrums in diese Basis liefert einen systematischen Farbfehler (Bias) und einen rgb-Wert, den man mit einer
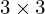 Matrix in die Koordinaten des Normfarbraums überführen kann.
Matrix in die Koordinaten des Normfarbraums überführen kann.Luther-Ives-Bedingung allgemein
- ist Voraussetzung für eine farbkonsistente Abbildung von Farben bei Kameras
- wenn die Sensorkurven der Kamera mit der gleichen Matrix aus der CIE-Normbasis hervorgehen, ist eine Abbildung von rgb nach XYZ mithilfe einer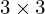 Matrix möglich
Matrix möglich
- das heißt auf deutsch: die Sensorkurven müssen fundamentale Metamere sein
- wenn die Sensorkurven der Kamera mit der gleichen Matrix aus der CIE-Normbasis hervorgehen, ist eine Abbildung von rgb nach XYZ mithilfe einer
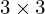 Matrix möglich
Matrix möglich- das heißt auf deutsch: die Sensorkurven müssen fundamentale Metamere sein
Transformation von rgb nach XYZ (bei einer schlechten Kamera)
- erst wird wieder zunächst die Farbmatrix bestimmt, z.B. durch Kenntnisse über die Sensorantwortkurve
- damit rechnet man leider falsche rgb-Wert in XYZ-Werte um, die damit fehlerbehaftet sind
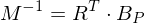
- der systematische Farbfehler kann nicht korrigiert werden, da für jedes Pixel das zugehörige Spektrum bekannt sein müsste
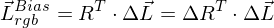
- damit rechnet man leider falsche rgb-Wert in XYZ-Werte um, die damit fehlerbehaftet sind
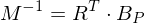
- der systematische Farbfehler kann nicht korrigiert werden, da für jedes Pixel das zugehörige Spektrum bekannt sein müsste
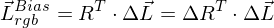
Wie ist das bei Bildschirmen?
- ein Bildschirm leuchtet mit den Primaries 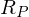
- das resultierende Spektrum eines rgb-Werts ist
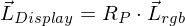
- der wahrnehmbare Farbeindruck ist
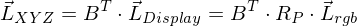
- der Farbeindruck bleibt identisch, egal ob ein Bildschirm mit beliebigen Spektren oder deren fundamentale Metamere leuchtet
- Farbmatrix für das Display:
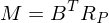
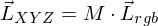
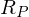
- das resultierende Spektrum eines rgb-Werts ist
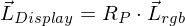
- der wahrnehmbare Farbeindruck ist
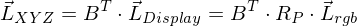
- der Farbeindruck bleibt identisch, egal ob ein Bildschirm mit beliebigen Spektren oder deren fundamentale Metamere leuchtet
- Farbmatrix für das Display:
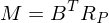
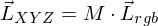
Zwischen-Zusammenfassung
- für eine Simulation genügen rgb-Wert nicht, man muss versuchen die Spektren selbst möglichst gut zu repräsentieren  spektrales Rendering
spektrales Rendering
- Luther-Ives-Bedingung für Kameras: farbkonsistente Interpretation der rgb-Farben einer Kamera ist nur möglich, wenn die Sensorkurven eine Linearkombination der Normabasis darstellen
- Umrechnung der rgb-Wert weist einen systematischen Fehler auf, der nicht korrigiert werden kann ohne Kenntnis des eingehenden Spektrums
- bei Bildschirmen gilt diese Bedingung nicht. Man kann beliebige Spektren verwenden, da sowieso nur die fundamentalen Metamere dieser wahrgenommen werden.
 spektrales Rendering
spektrales Rendering- Luther-Ives-Bedingung für Kameras: farbkonsistente Interpretation der rgb-Farben einer Kamera ist nur möglich, wenn die Sensorkurven eine Linearkombination der Normabasis darstellen
- Umrechnung der rgb-Wert weist einen systematischen Fehler auf, der nicht korrigiert werden kann ohne Kenntnis des eingehenden Spektrums
- bei Bildschirmen gilt diese Bedingung nicht. Man kann beliebige Spektren verwenden, da sowieso nur die fundamentalen Metamere dieser wahrgenommen werden.
Color Matching Experiment: eigenes Experiment mit Monitor
Kann man die Referenzspektren für das eigene Experiment mit einem Monitor erzeugen?
- nein, denn dann würden linear abhängige Spektren erzeugt werden; der maximale Range wäre 3
Kann man die Primärspektren des Monitors verwenden?
- im Prinzip ja, aber das Problem ist das Gamut = Größe des Farbraums
[Erklärung: siehe Vorlesungs-Video?]
- nein, denn dann würden linear abhängige Spektren erzeugt werden; der maximale Range wäre 3
Kann man die Primärspektren des Monitors verwenden?
- im Prinzip ja, aber das Problem ist das Gamut = Größe des Farbraums
[Erklärung: siehe Vorlesungs-Video?]
Zu messende Charakteristika bei Ausgabegeräten
- Aufwärmphase des Monitors
- Gamma-Funktion = elektro-optische Transferfunktion; Potenzfunktion oder ein-dimensionale LUT
- Kanalunabhängigkeit: messe die Leuchtdichte verschiedener rgb-Wert und prüfe, ob sie der Summe der drei Werte entsprechen
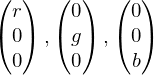
- Farbartkonstanz: Rampen sind die drei Primärspektren für r,g,b, die äquidistanz abgetastet werden und für die die entspr. XYZ-Werte gemessen werden. Übertragen in das Diagramm der Normfarbwertanteile (x,y), müssten alle gemessenen WErte für eien Rampe auf einem Punkt landen
- Schwarzwertkorrektur: Messung des rgb-Wertes (0,0,0) in XYZ und abziehen von den Rampen
- räumliche Homogenität: von dieser hängt ab, wie viele Bereiche vermessen werden müssen (anstatt wie bislang eher für einen Pixel)
- Gamma-Funktion = elektro-optische Transferfunktion; Potenzfunktion oder ein-dimensionale LUT
- Kanalunabhängigkeit: messe die Leuchtdichte verschiedener rgb-Wert und prüfe, ob sie der Summe der drei Werte entsprechen
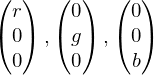
- Farbartkonstanz: Rampen sind die drei Primärspektren für r,g,b, die äquidistanz abgetastet werden und für die die entspr. XYZ-Werte gemessen werden. Übertragen in das Diagramm der Normfarbwertanteile (x,y), müssten alle gemessenen WErte für eien Rampe auf einem Punkt landen
- Schwarzwertkorrektur: Messung des rgb-Wertes (0,0,0) in XYZ und abziehen von den Rampen
- räumliche Homogenität: von dieser hängt ab, wie viele Bereiche vermessen werden müssen (anstatt wie bislang eher für einen Pixel)
Charakterisierungsmodelle
- MG (Matrix, gamma)
- MGO (Matrix, gamma, offset)
- 3-D LUT: hier werden die Rampen abgetastet, vermessen und bilden eine 3-D Abbildungstabelle
- räumliche Homogenität: Vermessung an verschiedenen Positionen am Bildschirm mit entsprechender Interpolation
- Gamut-Mapping: Falls außerhalb des Raums der darstellbaren Farben
- MGO (Matrix, gamma, offset)
- 3-D LUT: hier werden die Rampen abgetastet, vermessen und bilden eine 3-D Abbildungstabelle
- räumliche Homogenität: Vermessung an verschiedenen Positionen am Bildschirm mit entsprechender Interpolation
- Gamut-Mapping: Falls außerhalb des Raums der darstellbaren Farben
Charakterisierung eines Ausgabegeräts: Motivation? Was bedeutet Kanalunabhängigkeit?
- geschieht vor der Kalibrierung des Geräts
- es geht darum, die Eigenschaften des Geräts zu überprüfen, da Kalibrierungsmethoden davon abhängen
- im Prinzip sucht man für das Gerät eine Abbildung, die für die angestrebte XYZ-Farbe die entsprechenden rgb-Werte liefert, mit denen das Display angesteuert werden muss. D.h.:
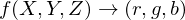
- Problem: Farbwerte, für die die zugehörigen XYZ-Farben gemessen werden müssten
Farbwerte, für die die zugehörigen XYZ-Farben gemessen werden müssten
- es geht darum, die Eigenschaften des Geräts zu überprüfen, da Kalibrierungsmethoden davon abhängen
- im Prinzip sucht man für das Gerät eine Abbildung, die für die angestrebte XYZ-Farbe die entsprechenden rgb-Werte liefert, mit denen das Display angesteuert werden muss. D.h.:
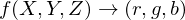
- Problem:
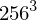 Farbwerte, für die die zugehörigen XYZ-Farben gemessen werden müssten
Farbwerte, für die die zugehörigen XYZ-Farben gemessen werden müsstenKoordinatentransformation: Orthonormale Basis
Hier sind Primär- und Konstruktionsbasis gleich. Orthonormale Koordinatensysteme werden in den meisten Fällen verwendet.
- gleiche Koordinatensysteme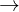 Linearkombination
Linearkombination
- unterschiedliche Koordinatensysteme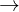 Projektion/Skalarprodukt
Projektion/Skalarprodukt
Zur Transformation benötigt man orthonormale Matrizen = Rotationsmatrizen. Deshalb gilt:
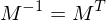 und
und 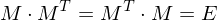
- gleiche Koordinatensysteme
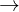 Linearkombination
Linearkombination- unterschiedliche Koordinatensysteme
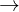 Projektion/Skalarprodukt
Projektion/SkalarproduktZur Transformation benötigt man orthonormale Matrizen = Rotationsmatrizen. Deshalb gilt:
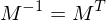 und
und 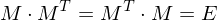
Koordinatentransformation: Beispiel Epipolargeometrie
- gegeben sei die Gleichung: 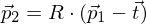
- interpretiere die Spalten / Zeilen von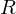 ; in welche Richtung zeigt t und in welchem Koordinatensystem ist der Vektor gegeben?
; in welche Richtung zeigt t und in welchem Koordinatensystem ist der Vektor gegeben?
Lösung:
- die Zeilen von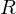 sind die Basisvektoren von
sind die Basisvektoren von 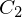 in
in 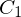 -Koordinaten (Achsen des Zielkoord.-Sys.)
-Koordinaten (Achsen des Zielkoord.-Sys.)
- die Spalten von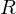 sind die Basisvektoren von
sind die Basisvektoren von 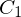 in
in 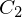 -Koordinaten (Achsen des Startkoord.-Sys.)
-Koordinaten (Achsen des Startkoord.-Sys.)
- Vektor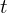 ist in
ist in 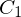 -Koordinaten gegeben
-Koordinaten gegeben
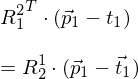
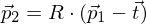
- interpretiere die Spalten / Zeilen von
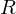 ; in welche Richtung zeigt t und in welchem Koordinatensystem ist der Vektor gegeben?
; in welche Richtung zeigt t und in welchem Koordinatensystem ist der Vektor gegeben?Lösung:
- die Zeilen von
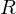 sind die Basisvektoren von
sind die Basisvektoren von 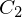 in
in 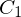 -Koordinaten (Achsen des Zielkoord.-Sys.)
-Koordinaten (Achsen des Zielkoord.-Sys.)- die Spalten von
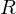 sind die Basisvektoren von
sind die Basisvektoren von 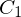 in
in 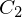 -Koordinaten (Achsen des Startkoord.-Sys.)
-Koordinaten (Achsen des Startkoord.-Sys.)- Vektor
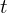 ist in
ist in 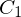 -Koordinaten gegeben
-Koordinaten gegeben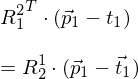
Szenengraph: Transformationsreihenfolge
Gegeben ist der Szenengraph (von oben nach unten): 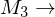 Karosserie
Karosserie 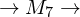 rechtes Vorderrad
rechtes Vorderrad 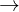 lokale Geometrie
lokale Geometrie
In welcher Reihenfolge stehen Translation/Rotation in einem Szenegraph?
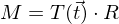
Wie ist die Reihenfolge der Gesamttransformation?
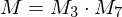
Wie ist die Reihenfolge in OpenGL (von oben nach unten)?
glTranslatef(...t3...);
glRotatef(...R3...);
glTranslatef(...t7...);
glRotatef(...R7...);
draw object
 Karosserie
Karosserie  rechtes Vorderrad
rechtes Vorderrad  lokale Geometrie
lokale GeometrieIn welcher Reihenfolge stehen Translation/Rotation in einem Szenegraph?
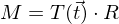
Wie ist die Reihenfolge der Gesamttransformation?
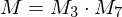
Wie ist die Reihenfolge in OpenGL (von oben nach unten)?
glTranslatef(...t3...);
glRotatef(...R3...);
glTranslatef(...t7...);
glRotatef(...R7...);
draw object
Unterschiede der Koordinatensysteme in CG und BV
CG Kamerakoodinaten
- Kamera im Ursprung
- x nach rechts
- y nach oben
- wir sehen entlang der negativen z-Achse
- Rechtssystem
BV Kamerakoodinaten
- Kamera im Ursprung
- x nach rechts
- y nach unten
- wir sehen entlang der positiven z-Achse
- Rechssystem
CG Pixelkoordinaten
- Ursprung unten links
- Bildauflösung B und H in Pixeln
- Blick entlang der z-Achse
- Linkssystem
BV Pixelkoordinaten
- Ursprung oben links
- Bildauflösung B und H in Pixeln
- Blick entlang der z-Achse
- Rechtssystem
- Kamera im Ursprung
- x nach rechts
- y nach oben
- wir sehen entlang der negativen z-Achse
- Rechtssystem
BV Kamerakoodinaten
- Kamera im Ursprung
- x nach rechts
- y nach unten
- wir sehen entlang der positiven z-Achse
- Rechssystem
CG Pixelkoordinaten
- Ursprung unten links
- Bildauflösung B und H in Pixeln
- Blick entlang der z-Achse
- Linkssystem
BV Pixelkoordinaten
- Ursprung oben links
- Bildauflösung B und H in Pixeln
- Blick entlang der z-Achse
- Rechtssystem



 ?
? eines Lichtreizes
eines Lichtreizes 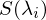 gemäss:
gemäss: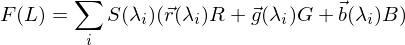
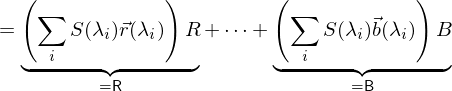

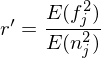
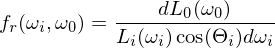
 -Koordinaten anhand des Lochkameramodells, bzw. duennes Linsenmodell?
-Koordinaten anhand des Lochkameramodells, bzw. duennes Linsenmodell?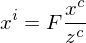
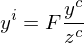
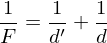
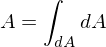
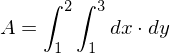
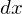 .
.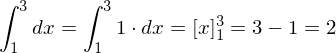
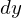
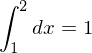
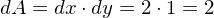
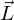
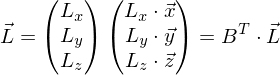
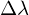 , um Gottes Willen, nicht vergessen! Denn das Skalaprodukt impliziert das.
, um Gottes Willen, nicht vergessen! Denn das Skalaprodukt impliziert das.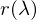 ,
, 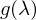 ,
, 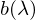 =
= 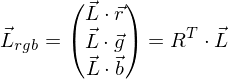

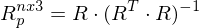
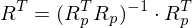
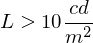

 ist bei Dämmerungssehen.
ist bei Dämmerungssehen. 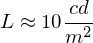
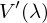 ist bei Nachtsehen.
ist bei Nachtsehen. 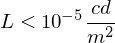
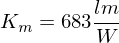
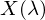
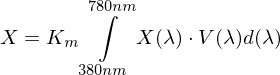
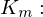 photometrisches Strahlungequivalent
photometrisches Strahlungequivalent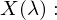 beliebiges Spektrum
beliebiges Spektrum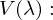
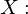 Koordinate in der Basis; nach Projektion der Funktion auf die Basisfunktion
Koordinate in der Basis; nach Projektion der Funktion auf die Basisfunktion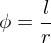 mit
mit  als Kreisbogen,
als Kreisbogen, 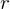 als Kreisradius
als Kreisradius
 führt zu
führt zu 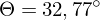
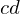
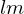 : 2000
: 2000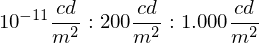
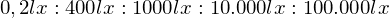

 als CIE Color-Matching Funktionen (Normspektralwertkurven) und
als CIE Color-Matching Funktionen (Normspektralwertkurven) und 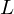 ,
,  als zwei verschiedene Spektren
als zwei verschiedene Spektren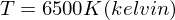
 als rekonstruiertes Spektrum,
als rekonstruiertes Spektrum,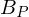 als Primaries der XYZ-Kurven (Rekonstruktionsbasis),
als Primaries der XYZ-Kurven (Rekonstruktionsbasis),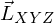 als Eingabespektrum
als Eingabespektrum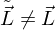 mit
mit 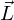 als Originalspektrum;
als Originalspektrum;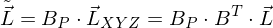
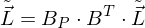
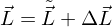
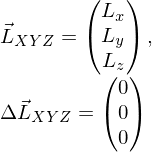
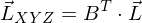 und
und 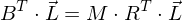 , woraus folgt:
, woraus folgt: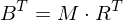
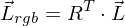 und
und 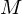 ist eine
ist eine 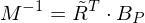
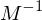 direkt berechnen:
direkt berechnen: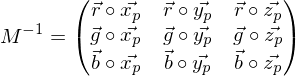
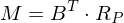
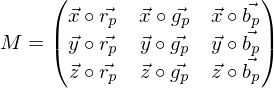
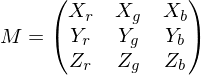
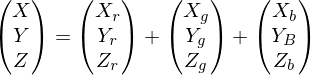
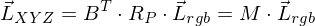
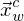 ist die x-Achse des Kamerakoordinatensystems
ist die x-Achse des Kamerakoordinatensystems 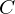 in Weltkoordinaten
in Weltkoordinaten  .
.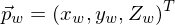 als Beispiel für einen Punkt in Weltkoordinaten
als Beispiel für einen Punkt in Weltkoordinaten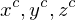 für die Achsen des Kamerakoord.-Sys. wird auch
für die Achsen des Kamerakoord.-Sys. wird auch 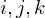 verwendet; anstatt
verwendet; anstatt 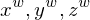 für die Achsen des Weltkoord.-Sys. auch
für die Achsen des Weltkoord.-Sys. auch 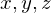
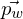 und
und