Wie ist ein Monoid definiert?
Gegeben sei eine Menge M und eine zweistellige Abbildung
 : M x M
: M x M  M. Wir benutzen meist die Infix-Schreibweise:
M. Wir benutzen meist die Infix-Schreibweise:
 (m
(m , m
, m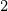 ) = m
) = m
 m
m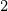 und bezeichnen
und bezeichnen  als zweistelligen Operator.
als zweistelligen Operator.
(M, ) heißt Monoid, falls folgendes gilt:
) heißt Monoid, falls folgendes gilt:
- ist assoziativ, d.h., es gilt m
ist assoziativ, d.h., es gilt m
 (m
(m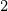
 m
m ) = (m
) = (m
 m
m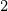 )
)  m
m
für alle m , m
, m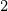 , m
, m
 M.
M.
- Es gibt ein neutrales Element e M, für das gilt:
M, für das gilt:
e m = m
m = m  e = m für alle m
e = m für alle m  M.
M.
 : M x M
: M x M  M. Wir benutzen meist die Infix-Schreibweise:
M. Wir benutzen meist die Infix-Schreibweise: (m
(m , m
, m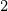 ) = m
) = m
 m
m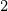 und bezeichnen
und bezeichnen  als zweistelligen Operator.
als zweistelligen Operator.(M,
 ) heißt Monoid, falls folgendes gilt:
) heißt Monoid, falls folgendes gilt:-
 ist assoziativ, d.h., es gilt m
ist assoziativ, d.h., es gilt m
 (m
(m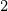
 m
m ) = (m
) = (m
 m
m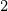 )
)  m
m
für alle m
 , m
, m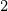 , m
, m
 M.
M.- Es gibt ein neutrales Element e
 M, für das gilt:
M, für das gilt:e
 m = m
m = m  e = m für alle m
e = m für alle m  M.
M.Tags: Algebraische Strukturen, VL 18.05.
Source:
Source:
Wie ist die Kurzschreibweise für Modulo-Rechnen und welche Modulo-Gesetze gibt es?
Wir denieren 
 =
= 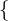 0, 1, ..., n - 1
0, 1, ..., n - 1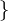 mit folgender Addition +
mit folgender Addition +
und Multiplikation
 . Seien k,
. Seien k, 
 Z
Z , dann gilt:
, dann gilt:
k +
 = (k +
= (k +  ) mod n
) mod n
k

 = (k
= (k 
 ) mod n
) mod n
(
 ,+
,+ ) und (
) und (
 ,
, 
 ) sind Monoide
) sind Monoide
(mit neutralen Elementen 0 bzw. 1)
Modulo-Gesetze
(a + b) mod n = ((a mod n) + (b mod n)) mod n
(a b) mod n = ((a mod n)
b) mod n = ((a mod n)  (b mod n)) mod n
(b mod n)) mod n
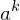 mod n =
mod n = 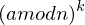 mod n
mod n

 =
= 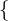 0, 1, ..., n - 1
0, 1, ..., n - 1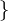 mit folgender Addition +
mit folgender Addition +
und Multiplikation

 . Seien k,
. Seien k, 
 Z
Z , dann gilt:
, dann gilt:k +

 = (k +
= (k +  ) mod n
) mod nk


 = (k
= (k 
 ) mod n
) mod n(

 ,+
,+ ) und (
) und (
 ,
, 
 ) sind Monoide
) sind Monoide(mit neutralen Elementen 0 bzw. 1)
Modulo-Gesetze
(a + b) mod n = ((a mod n) + (b mod n)) mod n
(a
 b) mod n = ((a mod n)
b) mod n = ((a mod n)  (b mod n)) mod n
(b mod n)) mod n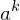 mod n =
mod n = 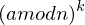 mod n
mod nTags: Algebraische Strukturen, VL 18.05.
Source:
Source:
Wie ist eine Gruppe definiert?
Ein Monoid 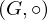 mit neutralem Element e heißt Gruppe, wenn zusätzlich zu den Monoid-Eigenschaften noch folgendes gilt:
mit neutralem Element e heißt Gruppe, wenn zusätzlich zu den Monoid-Eigenschaften noch folgendes gilt:
Für jedes gibt es ein
gibt es ein 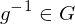 mit
mit  .
.
Dabei heißt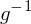 das Inverse von
das Inverse von 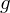 .
.
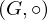 heißt kommutative Gruppe (oder abelsche Gruppe), falls außerdem
heißt kommutative Gruppe (oder abelsche Gruppe), falls außerdem  für alle
für alle  gilt.
gilt.
Bemerkung: In jeder Gruppe gilt nicht nur , sondern auch
, sondern auch 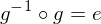 für alle
für alle  .
.
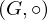 mit neutralem Element e heißt Gruppe, wenn zusätzlich zu den Monoid-Eigenschaften noch folgendes gilt:
mit neutralem Element e heißt Gruppe, wenn zusätzlich zu den Monoid-Eigenschaften noch folgendes gilt:Für jedes
 gibt es ein
gibt es ein 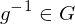 mit
mit  .
.Dabei heißt
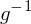 das Inverse von
das Inverse von 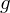 .
.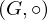 heißt kommutative Gruppe (oder abelsche Gruppe), falls außerdem
heißt kommutative Gruppe (oder abelsche Gruppe), falls außerdem  für alle
für alle  gilt.
gilt.Bemerkung: In jeder Gruppe gilt nicht nur
 , sondern auch
, sondern auch 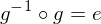 für alle
für alle  .
.Tags: Algebraische Strukturen, VL 18.05.
Source:
Source:
Tags: Algebraische Strukturen, VL 18.05.
Source:
Source:
Existieren in ( \
\ ) alle multiplikativen Inversen, wenn n keine Primzahl ist?
) alle multiplikativen Inversen, wenn n keine Primzahl ist?
 \
\ ) alle multiplikativen Inversen, wenn n keine Primzahl ist?
) alle multiplikativen Inversen, wenn n keine Primzahl ist?Nein.
Erläuterung s. Vorlesung.
Erläuterung s. Vorlesung.
Tags: Algebraische Strukturen, VL 18.05.
Source:
Source:
Tags: Algebraische Strukturen, VL 18.05.
Source:
Source:
Was sind Körper und welche Axiome gelten für Sie? Nenne je win Beispiel und ein Gegenbeipiel für Körper!




Tags: Algebraische Strukturen, VL 18.05.
Source:
Source:
Flashcard set info:
Author: P-H-I-L
Main topic: Mathematik
Topic: Mathematische Strukturen
Published: 13.04.2010
Card tags:
All cards (50)
Algebraische Strukturen (10)
Äquivalenzklasse (1)
Funktionen (7)
Grundlagen (1)
Kreuzprodukt (1)
Leere Menge (1)
Mengen Ordnung (1)
Mengendifferenz (1)
Potenzmenge (2)
Relation (2)
Relationen (8)
Teilmenge (1)
Vereinigung (1)
VL 18.05. (10)
VL vom 4.5.10 (10)
Zahlen 04.05.10 (1)













