Methodologie im Bereich Finanzwirtschaft


Quantitative Lösungen für komplexe Probleme.
| Anwendung eines zweistufigen Entscheidungsprozesses: |
| Ausdrücken aller Konsequenzen einer Entscheidung in Zahlungen |
| Aggregation aller Zahlungen. |
| Dieser Entscheidungsprozess heißt typischerweise “Bewertung”. |
Tags: bewertung, methodologie
Quelle: IuF Teil 1, Folie 3
Quelle: IuF Teil 1, Folie 3
Bewertung eines Wertpapiers mit sicheren Zahlungen 1/5


Der Betrag entspricht genau dem Barwert von €1000:
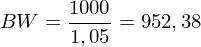
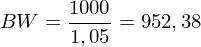
Tags: bewertung, wertpapier
Quelle: IuF Teil 4, Folie 4
Quelle: IuF Teil 4, Folie 4
Bewertung eines Wertpapiers mit sicheren Zahlungen 2/5


| Es gibt also demzufolge zwei Wege, die Zahlung von €1.000 in einem Jahr zu erhalten: (1) durch den Kauf des Wertpapiers oder (2) durch die Anlage von €952, 38 zum risikolosen Zinssatz. | |
| Die Behauptung ist nun, dass der Preis für das Wertpapier in einem normalen Markt €952,38 betragen muss. |
Tags: bewertung, wertpapier
Quelle: IuF Teil 4, Folie 5
Quelle: IuF Teil 4, Folie 5
Bewertung eines Wertpapiers mit sicheren Zahlungen 3/5
Angenommen, der Preis betrüge €940. Welche Arbitragegelegenheit ergibt sich in diesem Fall?

Angenommen, der Preis betrüge €940. Welche Arbitragegelegenheit ergibt sich in diesem Fall?

Wir können das Wertpapier kaufen und gleichzeitig einen Kredit in Höhe von €952,38 aufnehmen!
Eine solche Strategie ermöglicht eine Zahlung von €12,38, ohne zu
einer zukünftigen Auszahlung zu führen.
| / | Zahlung Heute | Zahlung in einem Jahr |
| Kaufe die Anleihe | -940,00 | +1000,00 |
| Leihe Geld von der Bank | +952,38 | -1000,00 |
| Netto-Zahlung | +12,38 | 0,00 |
Eine solche Strategie ermöglicht eine Zahlung von €12,38, ohne zu
einer zukünftigen Auszahlung zu führen.
Tags: bewertung, wertpapier
Quelle: IuF Teil 4, Folie 6
Quelle: IuF Teil 4, Folie 6
Bewertung eines Wertpapiers mit sicheren Zahlungen 4/5


In diesem Fall können wir das Wertpapier (leer)verkaufen und einen Betrag von €952,38 zum risikolosen Zinssatz anlegen.
Dies führt zu einem aktuellen Mittelzufluss von €7,62, dem kein zukünftiger Mittelabfluss gegenübersteht.
Bemerkung: Wenn wir das Wertpapier ursprünglich nicht besitzen, spricht man von einem Leerverkauf.
| / | Zahlung Heute | Zahlung in einem Jahr |
| Verkaufe die Anleihe | +960,00 | -1000,00 |
| Lege Geld bei der Bank an | -952,38 | +1000,00 |
| Netto-Zahlung | +7,62 | 0,00 |
Dies führt zu einem aktuellen Mittelzufluss von €7,62, dem kein zukünftiger Mittelabfluss gegenübersteht.
Bemerkung: Wenn wir das Wertpapier ursprünglich nicht besitzen, spricht man von einem Leerverkauf.
Tags: bewertung, leerverkauf, wertpapier
Quelle: IuF Teil 4, Folie 7
Quelle: IuF Teil 4, Folie 7
Bewertung eines Wertpapiers mit sicheren Zahlungen 5/5


| Martktteilnehmer, die Arbitragegelegenheiten entdecken, kaufen bzw. verkaufen das Wertpapier, so dass sich dessen Preis verändert und schnell den Wert von €952, 38 erreicht und die Arbitragegelegenheit verschwindet. | |
| Diesen Preis bezeichnet man auch als “No-Arbitrage-Preis”. | |
| Die Abwesenheit von Arbitragegelegenheiten in normalen Märkten impliziert, dass dort das so genannte Gesetz des einen Preises gilt. | |
| Das Gesetz des einen Preises besagt, dass zahlungsäquivalente Wertpapiere, die in verschiedenen normalen Märkten gehandelt werden, den gleichen Preis besitzen müssen. |
Tags: arbitragegelegenheit, bewertung, gesetz des einen preises, no-arbitrage-preis, normaler markt, wertpapier
Quelle: IuF Teil 4, Folie 8
Quelle: IuF Teil 4, Folie 8
Die Bewertung von Portfolios


Das Gesetz des einen Preises impliziert, dass Wertpapier C und das Portfolio aus A und B den gleichen Preis aufweisen müssen:
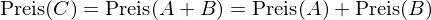
Die Beziehung zwischen des Wertes der einzelnen Wertpapiere eines Portfolios und dem Portfoliowert bezeichnet man als Wertadditivität.
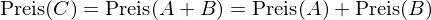
Die Beziehung zwischen des Wertes der einzelnen Wertpapiere eines Portfolios und dem Portfoliowert bezeichnet man als Wertadditivität.
Tags: bewertung, portfolio, wertadditivität
Quelle: IuF Teil 4, Folie 10
Quelle: IuF Teil 4, Folie 10
Bewertung von Wertpapieren (Zusammenfassung)


| Wenn die Zahlungen des betrachteten Wertpapiers durch existierende Wertpapiere vollständig nachgebildet werden können, so ist dessen Wert durch das Gesetz des einen Preises bestimmt. | |
| Wenn die Zahlungen des Wertpapiers nicht durch existierende Wertpapiere nachgebildet werden können, bestimme die erwarteten Zahlungen an jedem Zeitpunkt und diskontiere diese mit dem Zinssatz, der die Risikoprämie korrekt abbildet. |
Tags: bewertung, risikoprämie, wertpapier. erwartete zahlungen
Quelle: IuF Teil 4, Folie 19
Quelle: IuF Teil 4, Folie 19
Bewertung risikoloser Anleihen: Zerobonds 1/2


Als risikolose Anleihen werden diejenigen bezeichnet, deren
Zahlungsstrom sicher ist.
Die Anleihen mit der einfachsten Zahlungsstruktur sind Zerobonds
(Nullkuponanleihen), deren einzige Zahlung die Rückzahlung des
Nennwerts bei Fälligkeit der Anleihe ist.
Die Beziehung zwischen Preis und internem Zinssatz eines Zerobond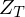 mit Fälligkeit zum Zeitpunkt
mit Fälligkeit zum Zeitpunkt 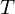 lässt sich ausdrücken als:
lässt sich ausdrücken als:
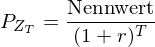
Zahlungsstrom sicher ist.
Die Anleihen mit der einfachsten Zahlungsstruktur sind Zerobonds
(Nullkuponanleihen), deren einzige Zahlung die Rückzahlung des
Nennwerts bei Fälligkeit der Anleihe ist.
Die Beziehung zwischen Preis und internem Zinssatz eines Zerobond
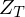 mit Fälligkeit zum Zeitpunkt
mit Fälligkeit zum Zeitpunkt 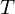 lässt sich ausdrücken als:
lässt sich ausdrücken als: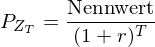
Tags: bewertung, risikolose anleihe, zerobond
Quelle: IuF Teil 4, Folie 20
Quelle: IuF Teil 4, Folie 20
Bewertung risikoloser Anleihen: Kuponanleihen 1/2


Bei Kuponbonds fallen außer der Rückzahlung des Nennwertes
zwischenzeitliche Zinszahlungen an (die Kupons).
Mit Hilfe des aus Zerobonds ermittelten risikolosen Zinssatzes lässt
sich ein risikoloser Kuponbond nach dem Gesetz des einen Preises bestimmen.
Beispiel: a) Bestimmen Sie den arbitragefreien Preis,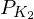 , einer zweijährigen Anleihe mit Nennwert 100 und einem jährlichen Kupon von 10% bei einem risikolosen Zinssatz von 5%.
, einer zweijährigen Anleihe mit Nennwert 100 und einem jährlichen Kupon von 10% bei einem risikolosen Zinssatz von 5%.
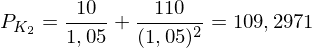
zwischenzeitliche Zinszahlungen an (die Kupons).
Mit Hilfe des aus Zerobonds ermittelten risikolosen Zinssatzes lässt
sich ein risikoloser Kuponbond nach dem Gesetz des einen Preises bestimmen.
Beispiel: a) Bestimmen Sie den arbitragefreien Preis,
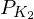 , einer zweijährigen Anleihe mit Nennwert 100 und einem jährlichen Kupon von 10% bei einem risikolosen Zinssatz von 5%.
, einer zweijährigen Anleihe mit Nennwert 100 und einem jährlichen Kupon von 10% bei einem risikolosen Zinssatz von 5%.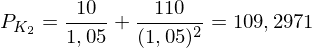
Tags: bewertung, kuponanleihe, risikolose anleihe, zerobond
Quelle: IuF Teil 4, Folie 23
Quelle: IuF Teil 4, Folie 23
Bewertung risikoloser Anleihen: Kuponanleihen 2/2
1. Nehmen sie an, der beobachtete Preis betrage 110. Zeigen Sie eine Strategie auf, die zu einem Arbitragegewinn führt
(Es existieren ein einjähriger und ein zweijähriger Zerobond, die jeweils einen Yield von 5% und einen Nennwert von 100 besitzen.)
2. Während Zerobonds unterhalb ihres Nennwerts notieren, ...
1. Nehmen sie an, der beobachtete Preis betrage 110. Zeigen Sie eine Strategie auf, die zu einem Arbitragegewinn führt
(Es existieren ein einjähriger und ein zweijähriger Zerobond, die jeweils einen Yield von 5% und einen Nennwert von 100 besitzen.)
2. Während Zerobonds unterhalb ihres Nennwerts notieren, ...

Tags: bewertung, kuponanleihe, kuponbond, riskolose anleihe, zerobond
Quelle: IuF Teil 4, Folie 24
Quelle: IuF Teil 4, Folie 24
Bewertung von Aktien


| Der von einer Aktie generierte Zahlungsstrom ist unsicher. | |
| Eine Duplikation des Zahlungsstroms mit anderen Wertpapieren (außer den eigenen sogenannten Derivaten) ist unwahrscheinlich. | |
| Daher wenden wir für die Aktienbewertung die Methode der Diskontierung der bei einem Aktieninvestment erwarteten Zahlungen an. | |
| An dieser Stelle konzentrieren wir uns auf die Bestimmung der erwarteten Zahlungen |
Tags: aktien, bewertung
Quelle: IuF Teil 4, Folie 27
Quelle: IuF Teil 4, Folie 27
Aktienbewertung: Investorin mit Einjahreshorizont


| Zum einen entstehen Zahlungen, wenn das Unternehmen während der Haltedauer Dividenden ausschüttet. Zum anderen entsteht ein Mittelzufluss, wenn die Investorin sich entscheidet, die Aktien zu veräußern. | |
| Betrachten wir hier eine Investorin mit einem Anlagehorizont von einem Jahr. Wenn es zu einer Dividendenzahlung während des Jahres kommt, dann erfolgt diese am Ende des Anlagezeitraums. | |
Die Zahlungen aus dem Investment sind die Auszahlung beim Erwerb in Zeitpunkt 0, 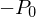 , sowie die Einzahlungen nach einem Jahr in Form des Veräußerungspreises, , sowie die Einzahlungen nach einem Jahr in Form des Veräußerungspreises, 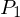 , plus evtl. einer Dividende, , plus evtl. einer Dividende, 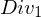 . . |
Tags: aktien, bewertung
Quelle: IuF Teil 4, Folie 28
Quelle: IuF Teil 4, Folie 28
Aktienbewertung: Dividend Discount Model 1/2


Als Bewertungsgleichung ergibt sich, wenn der adäquate, das Risiko
berücksichtigende Diskontierungssatz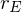 beträgt:
beträgt:
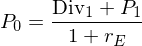
Die Investorin muss also sowohl die erwartete Dividende als auch den erwarteten Veräußerungspreis bestimmen.
Der Veräußerungspreis bestimmt sich aus dem Kalkül eines anderen Investors, dessen Bewertungsgleichung lautet:
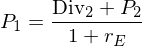
Damit wird die Gleichung der ursprünglichen Investorin zu:
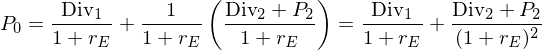
berücksichtigende Diskontierungssatz
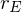 beträgt:
beträgt: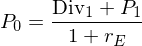
Die Investorin muss also sowohl die erwartete Dividende als auch den erwarteten Veräußerungspreis bestimmen.
Der Veräußerungspreis bestimmt sich aus dem Kalkül eines anderen Investors, dessen Bewertungsgleichung lautet:
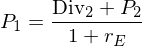
Damit wird die Gleichung der ursprünglichen Investorin zu:
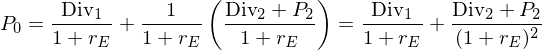
Tags: aktie, bewertung, Dividend Discount Model
Quelle: IuF Teil 4, Folie 29
Quelle: IuF Teil 4, Folie 29
Aktienbewertung: Dividend Discount Model 2/2


Durch weitere Anwendung dieser Logik ergibt sich der Wert einer
Aktie als:
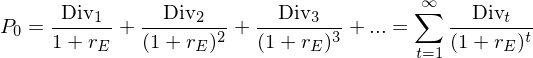
Dies bedeutet, dass der Preis einer Aktie sich ergibt als Barwert aller erwarteten Dividendenzahlungen.
Insbesondere impliziert dieses Resultat, dass der Anlagehorizont für den Wert einer Aktie unerheblich ist. Da bei Veräußerung immer ein Käufer gefunden werden muss, sind in jedem Fall die gesamten zukünftigen Zahlungen einer Aktie für deren Bewertung relevant.
Aktie als:
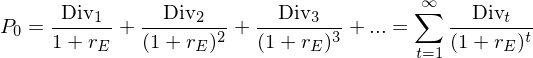
Dies bedeutet, dass der Preis einer Aktie sich ergibt als Barwert aller erwarteten Dividendenzahlungen.
Insbesondere impliziert dieses Resultat, dass der Anlagehorizont für den Wert einer Aktie unerheblich ist. Da bei Veräußerung immer ein Käufer gefunden werden muss, sind in jedem Fall die gesamten zukünftigen Zahlungen einer Aktie für deren Bewertung relevant.
Tags: aktie, bewertung, dividend discount model
Quelle: IuF Teil 4, Folie 30
Quelle: IuF Teil 4, Folie 30
Kartensatzinfo:
Autor: sundance
Oberthema: BWL
Thema: Unternehmensführung
Schule / Uni: KIT
Ort: Karlsruhe
Veröffentlicht: 12.04.2010
Schlagwörter Karten:
Alle Karten (103)
abzinsen (1)
aktie (4)
aktien (4)
arbitrage (1)
aufzinsen (1)
Barwert (4)
barwert (1)
bewertung (15)
CAPM (1)
capm (1)
commercial paper (1)
covenants (1)
eigenkapital (1)
Endliche Rente (1)
endwert (2)
Endwert (3)
ertrag (1)
Erwartungswert (1)
Ewige Rente (1)
fazit (1)
finanzierung (2)
finanzwirtschaft (1)
fremdkapital (1)
Gleichgewicht (6)
gleichgewicht (1)
Individualkalkül (3)
industrieanleihe (1)
investition (3)
kapitalwert (4)
kapitalwertrate (5)
kernprinzipien (3)
Kombinationen (5)
kreditarten (2)
kreditlinie (1)
kuponanleihe (2)
kuponbond (1)
kuponzahlung (1)
leerverkauf (1)
methodologie (1)
normaler markt (2)
portefeuilles (1)
Portefeuilles (8)
portfeuilles (1)
portfolio (2)
Rendite (5)
rendite (1)
renditen (1)
rentabilität (1)
Rentenformeln (4)
rentenformeln (1)
risiko (3)
Risiko (7)
risikoaversion (3)
risikoprämie (3)
stammaktien (1)
statisiken (1)
tilgungsformen (1)
vermögenswerte (1)
vorzugsaktien (1)
wandelanleihe (1)
wertadditivität (1)
wertpapier (6)
wertschöfpung (1)
zerobond (3)
zinsformen (1)



