Was versteht man unter "Messen"?
Messen ist die Bestimmung der Ausprägung einer Eigenschaft eines (Mess-)Objekts und erfolgt durch eine Zuordnung von Zahlen zu Messobjekten. (Orth, 1995)
.... wobei allerdings eine "Zurodnung von Zahlen zu Messobjekten ... nur dann eine Messung ist, "wenn die Zahlen ("Messwerte") empirische Sachverhalte ausdrücken, d.h. wenn die (numerischen) Beziehungen zwischen Messwerten empirischen Beziehungen zwischen den Messobjekten ausdrücken."
.... wobei allerdings eine "Zurodnung von Zahlen zu Messobjekten ... nur dann eine Messung ist, "wenn die Zahlen ("Messwerte") empirische Sachverhalte ausdrücken, d.h. wenn die (numerischen) Beziehungen zwischen Messwerten empirischen Beziehungen zwischen den Messobjekten ausdrücken."
Tags: Messen, Skalierung
Source: S83
Source: S83
Was definiert die "Schwierigkeit" einer Aufgabe bei der Klassischen Testtheorie und bei Persönlichkeitsfragebögen?
Im einfachsten Fall, bei dichotom zu verrechnenden Aufgaben eines Leistungstests (richtig vs. falsch), ergibt sich die (Item-)Schwierigkeit laut Klassischer Testtheorie als die relative Lösungshäufigkeit, mit der eine Aufgabe in der Eichstichprobe gelöst wurde.
Bei mehrkategoriell zu verrechnenden Aufgaben können zwar die relativen Häufigkeiten bestimmt werden, mit denen die einzelnen Kategorien in einer (Eich-)Stichprobe realisiert wurden, die Bezeichnung als "Schwierigkeit" ist aber pro Kategorie unüblich.
Demgegenüber wird die Bezeichnung "Schwierigkeit" häufig auch bei dichotom zu verrechnenden Items eines Persönlichkeitsfragebogens verwendet, obwohl es inhaltlich treffender wäre, vom "Grad der Herausforderung" zu sprechen, mit dem ein Item die Tp konfrontiert, in bestimmter Weise zu reagieren.
Bei mehrkategoriell zu verrechnenden Aufgaben können zwar die relativen Häufigkeiten bestimmt werden, mit denen die einzelnen Kategorien in einer (Eich-)Stichprobe realisiert wurden, die Bezeichnung als "Schwierigkeit" ist aber pro Kategorie unüblich.
Demgegenüber wird die Bezeichnung "Schwierigkeit" häufig auch bei dichotom zu verrechnenden Items eines Persönlichkeitsfragebogens verwendet, obwohl es inhaltlich treffender wäre, vom "Grad der Herausforderung" zu sprechen, mit dem ein Item die Tp konfrontiert, in bestimmter Weise zu reagieren.
Tags: Klassische Testtheorie, Persönlichkeitsfragebogen, Schwierigkeit, Skalierung
Source: S83
Source: S83
Was ist das Problem von Testungen unter "Speed-and-Power"-Bedingungen in Bezug auf die Skalierung?
Skalierung als Gütekriterium bezieht sich auf die Eindimensionalität eines Tests und ob die Verrechnung zu Testwerten empirisch begründet ist.
Bei Testungen unter "Speed-and-Power" Bedingungen werden häufig zwei Eigenschaften vermengt, nämlich die Fähigkeit, bestimmte Anforderungen - auch schwierige - grundsätzlich zu erfüllen, mit der Fähigkeit, dies auch (hinreichend) schnell zu können.
Daher ist die Voraussetzung der Eindimensionalität nicht gegeben.
Bei Testungen unter "Speed-and-Power" Bedingungen werden häufig zwei Eigenschaften vermengt, nämlich die Fähigkeit, bestimmte Anforderungen - auch schwierige - grundsätzlich zu erfüllen, mit der Fähigkeit, dies auch (hinreichend) schnell zu können.
Daher ist die Voraussetzung der Eindimensionalität nicht gegeben.
Tags: Skalierung
Source: S84
Source: S84
Welche Probleme können bei einer Faktorenanalyse für dichotome zu verrechnende Items entstehen? Welche Ansätze könnten stattdessen angewendet werden?
(Kapitel Skalierung)
Die (herkömmliche, weil auf Intervallsksala aufbauende) Faktorenanalyse funktioniert im beabsichtigten Zusammenhang allerdings höchstens bei nicht dichotom zu verrechnenden Items.
Testbatterien mit dichotom zu verrechnenden Items, die auf Faktorenanalyse beruhen und dementsprechend je Untertest Eindimensionalität behaupten, genügen diesem Anspruch nur vordergründig.
Zum Beispiel Guttmann (1955) hat schon vor langer Zeit gezeigt, dass die Anwendung der Faktorenanalyse auf dichotome Variablen stets zu artifiziellen Faktoren führt. Lange bekannt, aber kaum umgesetzt ist auch, dass die Lösung des Problems die Verwendung eines anderen, besonderen Korrelationsmaßes wäre; nämlich der tetrachorischen statt der obligaten Pearson-Korrelation.
Und vor allem gäbe es im Rahmen der sog. "linearen Strukturgleichungsmodell" Ansätze, die als Faktorenanalyse für dichotome Daten gelten können.
Beispiel: Erklärung siehe Seite 85

Die (herkömmliche, weil auf Intervallsksala aufbauende) Faktorenanalyse funktioniert im beabsichtigten Zusammenhang allerdings höchstens bei nicht dichotom zu verrechnenden Items.
Testbatterien mit dichotom zu verrechnenden Items, die auf Faktorenanalyse beruhen und dementsprechend je Untertest Eindimensionalität behaupten, genügen diesem Anspruch nur vordergründig.
Zum Beispiel Guttmann (1955) hat schon vor langer Zeit gezeigt, dass die Anwendung der Faktorenanalyse auf dichotome Variablen stets zu artifiziellen Faktoren führt. Lange bekannt, aber kaum umgesetzt ist auch, dass die Lösung des Problems die Verwendung eines anderen, besonderen Korrelationsmaßes wäre; nämlich der tetrachorischen statt der obligaten Pearson-Korrelation.
Und vor allem gäbe es im Rahmen der sog. "linearen Strukturgleichungsmodell" Ansätze, die als Faktorenanalyse für dichotome Daten gelten können.
Beispiel: Erklärung siehe Seite 85

Tags: Faktorenanalyse, Skalierung
Source: S84
Source: S84
Welche Rolle spielt die Skalierung in der Klassischen Testtheorie?
(Skalierung als Gütekriterium bezieht sich bei gegebener Eindimensionalität eines Tests darauf, ob die Verrechnung zu Testwerten empirisch begründet ist.)
Die Methoden der klassischen Testtheorie sind völlig ungeeignet, einen Test hinsichtlich des Gütekriteriums Skalierung zu prüfen und deshalb gibt es dieses Gütekriterium in diesem Ansatz gar nicht.
Im Zusammenhang mit der Skalierung verwendet die klassische Testtheorie folgende Methoden (in denen es vor allem um die Zusammenfassung von Items zu Tests geht):
Die Zielsetzung eindimensionaler Messungen entsprechend soll die innere Konsistenz eines Tests möglichst groß sein: Die Items ein und desselben Tests sollen gemeinsam auf einen einzigen Faktor laden und die Interkorrelationen aller Items nahzu 1 betragen.
Des Weiteren fordert die klassische Testtheorie bei der Itemzusammenstellung eines Test auch

Die Methoden der klassischen Testtheorie müssen jedoch grundsätzlich kritisiert werden. Sie sind alle stichprobenabhängig.
(Abbildung unten zeigt, dass die Korrelation der Testwerte zweier Aufgaben für 2 Teilstichproben gänzlich andere Werte annehmen kann als für die Gesamtstichprobe.)

Anders als die Klassische Testtheorie kann die Item-Response-Theorie durchaus prüfen, ob die gegebenen Verrechnungsvorschriften eines Tests zu Testwerten führen, die verhaltensadäquate Relationen wiedergeben.
Die Methoden der klassischen Testtheorie sind völlig ungeeignet, einen Test hinsichtlich des Gütekriteriums Skalierung zu prüfen und deshalb gibt es dieses Gütekriterium in diesem Ansatz gar nicht.
Im Zusammenhang mit der Skalierung verwendet die klassische Testtheorie folgende Methoden (in denen es vor allem um die Zusammenfassung von Items zu Tests geht):
- Innere Konsistenz
- Faktorenanalyse
- Interkorrelationen
Die Zielsetzung eindimensionaler Messungen entsprechend soll die innere Konsistenz eines Tests möglichst groß sein: Die Items ein und desselben Tests sollen gemeinsam auf einen einzigen Faktor laden und die Interkorrelationen aller Items nahzu 1 betragen.
Des Weiteren fordert die klassische Testtheorie bei der Itemzusammenstellung eines Test auch
- dass sich die Schwierigkeit des Items gleichmäßig innerhalb des Intervalls (0,05 bis 0,95) verteilen,
- dass die sog. "Trennschärfeindizes" der Items (das sind die Korrelationen des Testwerts pro Item mit dem Testwert aus allen übrigen Items) sehr hohe Werte annehmen.

Die Methoden der klassischen Testtheorie müssen jedoch grundsätzlich kritisiert werden. Sie sind alle stichprobenabhängig.
(Abbildung unten zeigt, dass die Korrelation der Testwerte zweier Aufgaben für 2 Teilstichproben gänzlich andere Werte annehmen kann als für die Gesamtstichprobe.)

Anders als die Klassische Testtheorie kann die Item-Response-Theorie durchaus prüfen, ob die gegebenen Verrechnungsvorschriften eines Tests zu Testwerten führen, die verhaltensadäquate Relationen wiedergeben.
Tags: Faktorenanalyse, Innere Konsistenz, Item-Response-Theorie, Klassische Testtheorie, Skalierung
Source: S84
Source: S84
Was ist der einfachste Verrechnungsmodus (Methode der Skalierung)? Welche Bedingung muss gelten, damit dieser Verrechnungsmodus fair ist?
Der einfachste Verrechnungsmodus sieht als Testkennwert die Anzahl gelöster Aufgaben vor. Das heißt, ungeachtet dessen, welche Aufgaben von einer Tp gelöst und welche nicht gelöst werden, zählen nur die "Treffer".
Fischer gibt dazu einen Beweis, wonach das (dichotome) logistische Testmodell von Georg Rasch - Rasch-Modell - notwendigerweise gelten muss, damit dieser Verrechnungsmodus fair ist.
Das Rasch-Modell beschreibt die Wahrscheinlichkeit, dass Tp Item
Item  löst (+), in Abhängigkeit des Personenparameters
löst (+), in Abhängigkeit des Personenparameters 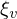 , das ist die (wahre) Fähigkeit von
, das ist die (wahre) Fähigkeit von  , und des Itemparameters
, und des Itemparameters 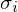 , das ist die (wahre) Schwierigkeit von
, das ist die (wahre) Schwierigkeit von  :
:

Weil sich dieses Modell als im statistischen Sinn stichprobenunabhängig herausstellt, kann auch ein besonderer Modelltest abgeleitet werden - somit muss es nie ungeprüft vorausgesetzt werden.
Fischer gibt dazu einen Beweis, wonach das (dichotome) logistische Testmodell von Georg Rasch - Rasch-Modell - notwendigerweise gelten muss, damit dieser Verrechnungsmodus fair ist.
Das Rasch-Modell beschreibt die Wahrscheinlichkeit, dass Tp
 Item
Item  löst (+), in Abhängigkeit des Personenparameters
löst (+), in Abhängigkeit des Personenparameters 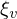 , das ist die (wahre) Fähigkeit von
, das ist die (wahre) Fähigkeit von  , und des Itemparameters
, und des Itemparameters 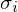 , das ist die (wahre) Schwierigkeit von
, das ist die (wahre) Schwierigkeit von  :
:
Weil sich dieses Modell als im statistischen Sinn stichprobenunabhängig herausstellt, kann auch ein besonderer Modelltest abgeleitet werden - somit muss es nie ungeprüft vorausgesetzt werden.
Tags: Rasch-Modell, Skalierung, Stichprobenunabhängig
Source: S88
Source: S88
Wie weit ist die Verbreitung der Rasch-Modell geprüften Tests?
An publizierten Tests, die den zur Diskussion stehenden Verrechnungsmodus beinhalten und dem Modell laut Modelltest entsprechen, existieren nach wie vor nur sehr wenige.
International beachtete Intelligenz-Testbatterien, die gemäß Rasch-Modell konstruiert wurden, sind folgende:
Regelmäßig erweisen sich Tests, die (noch) ohne entsprechende Prüfung entwickelt wurden als nicht verrechnungsfair: Das Rasch-Modell gilt nicht. Um nur einige bedeutende Beispiele zu nennen:
International beachtete Intelligenz-Testbatterien, die gemäß Rasch-Modell konstruiert wurden, sind folgende:
- BAS II (British Ability Scales II) - nicht mehr vertrieben,
- DAS bzw. DAS II (Differential Ability Scales - Second Edition, 2007) - amerik. Version des BAS
- K-ABC (Kaufman Assessment Battery for Children) - deutschspr. Edition von Melchers & Preus, 1991
- AID 2 (deutsch, türkisch, italienisch, ungarisch) - eine englischsprachige Version ist in Vorbereitung.
Regelmäßig erweisen sich Tests, die (noch) ohne entsprechende Prüfung entwickelt wurden als nicht verrechnungsfair: Das Rasch-Modell gilt nicht. Um nur einige bedeutende Beispiele zu nennen:
- SPM (Standard Progressive Matrices, John C. Raven): gravierende Modellabweichungen festgestellt
- HAWIK-IV - frühere Versionen; für betroffene Untertests laut der Monografie von Kubinger (1983) in Bezug auf den HAWIK und laut Steuer (1988) in Bezug auf den HAWIK-R gravierende Modellabweichungen festgestellt. Beispiele: - Untertest Allgemeines Wissen (HAWIK-R): Aufgaben besitzen abhängig vom Geschlecht unterschiedliche (relative) Schwierigkeiten ("Welche Farbe erhält man wenn man die Farben Blau und Gelb miteinander vermischt?" ... bevorzugt Mädchen // "Wie viele Menschen gibt es auf der Welt?" ... bevorzugt Jungen) .. der Test misst also auch das Geschlecht.- Untertest Allgemeines Wissen (HAWIK): Aufgabe "Was musst du tun, damit das Wasser kocht?" ist für leistungsschwache Kinder leichter zu beantworten als für leistungsstarke Kinder.(ist auch im aktuellen HAWIK-IV enthalten)
Tags: Rasch-Modell, Skalierung
Source: S92
Source: S92
Wie kann die Überprüfung des Rasch-Modells bei nicht-dichotomen Antwortformat erfolgen?
Welche Ergebnisse zeigten die Überprüfungen mittels Rasch-Modell?
Welche Ergebnisse zeigten die Überprüfungen mittels Rasch-Modell?
Für bestimmte andere Verrechnungsmodi existieren innerhalb der Item-Response -Theorie andere Modelle bzw. Verallgemeinerungen des Rasch-Modells, die teilweise analoge Bedeutung haben. Wenn etwa zusätzlich zur Bewertung in richtig/falsch, teilrichtige Antworten berücksichtigt und verrechnet werden, dann müssten sich die mit dem mehrkategoriellen mehrdimensionalen Rasch-Modell gewonnene Itemkategorienparameter (für z.B. "teilw. richtig"/1 Punkt, "vollkommen richtig"/2 Punkte) über alle Items hinweg in der behaupteten Relation zueinander verhalten (im Beispiel also 1:2).
Entsprechende Modelltests bei Tests angewendet, die bei ihrer Entwicklung (noch) nicht daraufhin geprüft wurden, dokumentieren erfahrungsgemäß deutlich, dass die Verrechnungsfairness nicht gegeben ist.
Beispiel: Anwendung des mehrkategoriell mehrdimensionalen Rasch-Modell geschätzten Itemparameter im Untertest Gemeinsamkeiten finden (HAWIK-R).
Die optimal angepasste Gerade weist auf einen Anstieg von 0,52 auf - wegen relativer Antworthäufigkeiten von 0,00 bzw. 1,00 musten einige Aufgaben aus der analyse ausgeschlossen werden.

Es ist einsichtig, dass umso strengere Voraussetzungen bzw. Modellansprüche an die Items zu stellen sind, je komplizierter der vorgesehene Verrechnungsmodus ist.
Entsprechende Modelltests bei Tests angewendet, die bei ihrer Entwicklung (noch) nicht daraufhin geprüft wurden, dokumentieren erfahrungsgemäß deutlich, dass die Verrechnungsfairness nicht gegeben ist.
Beispiel: Anwendung des mehrkategoriell mehrdimensionalen Rasch-Modell geschätzten Itemparameter im Untertest Gemeinsamkeiten finden (HAWIK-R).
Die optimal angepasste Gerade weist auf einen Anstieg von 0,52 auf - wegen relativer Antworthäufigkeiten von 0,00 bzw. 1,00 musten einige Aufgaben aus der analyse ausgeschlossen werden.

Es ist einsichtig, dass umso strengere Voraussetzungen bzw. Modellansprüche an die Items zu stellen sind, je komplizierter der vorgesehene Verrechnungsmodus ist.
Tags: Rasch-Modell, Skalierung
Source: S93
Source: S93
Flashcard set info:
Author: coster
Main topic: Psychologie
Topic: Psychologische Diagnostik
School / Univ.: Universität Wien
City: Wien
Published: 12.06.2013
Tags: SS2013, Holocher-Ertl
Card tags:
All cards (119)
16 PF-R (3)
AIST-R/UST-R (2)
Aufmerksamkeit (1)
Beobachten (1)
Big Five (1)
culture-fair (5)
Definition (3)
Diagnostik (15)
Eichmaßstäbe (3)
Eichung (9)
Eigenschaft (1)
Ethik (1)
Fairness (7)
Faktorenanalyse (2)
Formal (8)
Fragen (3)
Freiwillige (1)
GIS (1)
Grundsätze (6)
Gruppenverfahren (1)
Gütekriterien (1)
Intelligenz (1)
Interessen (4)
IQ (1)
Konzentration (1)
Laien (1)
Leistungsdiagnostik (13)
Memory (1)
Merkmal (1)
Messen (1)
NEO-PI-R (2)
Nützlichkeit (2)
Objektivität (5)
Ökonomie (3)
Postkorb (1)
Profil (1)
Prognose (1)
Prozentrang (2)
Prüfen (3)
Psychologe (1)
Rasch-Modell (5)
Reasoning (1)
Reliabilität (6)
Schwierigkeit (1)
Skalierung (8)
Space (1)
Test (2)
trait (1)
Validität (8)
Verfahren (3)
Voraussetzung (1)
Zumutbarkeit (2)



