Wie definiert man eine Menge?
Aufzählung oder Menge von Elementen mit einer bestimmten Eigenschaft.
Tags: Grundlagen
Source:
Source:
Gegeben ist R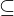 A x A und a
A x A und a  A. Wie lautet die Äquivalenzklasse von a?
A. Wie lautet die Äquivalenzklasse von a?
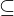 A x A und a
A x A und a  A. Wie lautet die Äquivalenzklasse von a?
A. Wie lautet die Äquivalenzklasse von a?[a]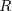 ={ a'
={ a'  A
A  a R a' }
a R a' }
Für zwei Elemente a, b A gilt entweder
A gilt entweder
[a]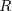 =[b]
=[b]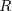 oder [a]
oder [a]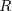
 [b]
[b]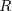 ={}.
={}.
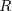 ={ a'
={ a'  A
A  a R a' }
a R a' }Für zwei Elemente a, b
 A gilt entweder
A gilt entweder[a]
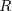 =[b]
=[b]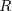 oder [a]
oder [a]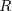
 [b]
[b]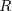 ={}.
={}.Tags: Äquivalenzklasse
Source: VL 2
Source: VL 2
Wann heißt eine Relation (partielle) Ordnung?
Eine Relation R 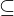 A x A heißt (partielle ) Ordnung, falls folgendes gilt:
A x A heißt (partielle ) Ordnung, falls folgendes gilt:
- Reflexivität: für alle a A gilt (a, a)
A gilt (a, a)  R
R
- Transitivität: falls für beliebige a, b, c A (a, b)
A (a, b)  R und (b, c)
R und (b, c)  R gilt, so muss auch (a,c)
R gilt, so muss auch (a,c)  R gelten.
R gelten.
- Antisymmetrie: falls für beliebige a, b A (a, b)
A (a, b)  R und (b, a)
R und (b, a)  R gelten, so muss a = b gelten, d.h., a und b sind dann gleich.
R gelten, so muss a = b gelten, d.h., a und b sind dann gleich.
Bei der Definition einer Ordnung hat sich gegenüber der Def. einer Äquivalenzrelation nur die letzte Eigenschaft geändert (Antisymmetrie vs. Symmetrie).
Achtung: Antisymmentrie ist nicht das Gegenteil von Symmetrie!
Jede Gleichheitsrelation erfüllt beide Eigenschaften.
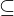 A x A heißt (partielle ) Ordnung, falls folgendes gilt:
A x A heißt (partielle ) Ordnung, falls folgendes gilt:- Reflexivität: für alle a
 A gilt (a, a)
A gilt (a, a)  R
R- Transitivität: falls für beliebige a, b, c
 A (a, b)
A (a, b)  R und (b, c)
R und (b, c)  R gilt, so muss auch (a,c)
R gilt, so muss auch (a,c)  R gelten.
R gelten.- Antisymmetrie: falls für beliebige a, b
 A (a, b)
A (a, b)  R und (b, a)
R und (b, a)  R gelten, so muss a = b gelten, d.h., a und b sind dann gleich.
R gelten, so muss a = b gelten, d.h., a und b sind dann gleich.Bei der Definition einer Ordnung hat sich gegenüber der Def. einer Äquivalenzrelation nur die letzte Eigenschaft geändert (Antisymmetrie vs. Symmetrie).
Achtung: Antisymmentrie ist nicht das Gegenteil von Symmetrie!
Jede Gleichheitsrelation erfüllt beide Eigenschaften.
Wofür stehen die Symbole  ,
,  ,
,  und
und  ?
?
 ,
,  ,
,  und
und  ?
? steht für die Menge der Natürlichen Zahlen mit 0
steht für die Menge der Natürlichen Zahlen mit 0 = {0, 1, 2, 3, 4, 5, ...}
= {0, 1, 2, 3, 4, 5, ...} steht für die Menge Ganzer Zahlen
steht für die Menge Ganzer Zahlen = {..., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ...}
= {..., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ...}Rationale Zahlen
 : die Menge aller Brüche (= Menge aller Kommazahlen mit endlicher oder periodischer Dezimaldarstellung)
: die Menge aller Brüche (= Menge aller Kommazahlen mit endlicher oder periodischer Dezimaldarstellung)2 -4

 0,75 32.3347
0,75 32.3347 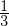 = 0,3333....
= 0,3333....Reelle Zahlen
 : Die Menge aller reelen Zahlen( = Menge aller Kommazahlen mit beliebiger - auch unendlicher, nicht-periodischer Dezimaldarstellung)
: Die Menge aller reelen Zahlen( = Menge aller Kommazahlen mit beliebiger - auch unendlicher, nicht-periodischer Dezimaldarstellung)2 -4

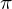 = 3,14159... e = 2,718281...
= 3,14159... e = 2,718281...Zeige ein Beispiel für die Beschreibung von Mengen als Aufzählung!
M = { 0, 2, 4, 6, 8, . . . }
Tags: Mengen Aufzählung
Source:
Source:
Wie beschreibt man eine Menge von Elementen mit bestimmten Eigenschaften?
Beispiel:
 ∈
∈  und n gerade
und n gerade 
Allgemeines Format:

(M ist Menge aller Elemente x, die die Eigenschaft P erfüllen.)
 ∈
∈  und n gerade
und n gerade 
Allgemeines Format:

(M ist Menge aller Elemente x, die die Eigenschaft P erfüllen.)
Tags: Mengen allgemeines Format
Source:
Source:
Wie ist die Anordnung innerhalb einer Menge?
Die Elemente einer Menge sind ungeordnet, d.h., ihre
Ordnung spielt keine Rolle. Beispielsweise gilt:
{ 1, 2, 3 } = { 1, 3, 2 } = { 2, 1, 3 } = { 2, 3, 1 } = { 3, 1, 2 } = { 3, 2, 1 }
Ein Element kann nicht “mehrfach” in einer Menge auftreten.
Es ist entweder in der Menge, oder es ist nicht in der Menge.
Beispielsweise gilt:

Ordnung spielt keine Rolle. Beispielsweise gilt:
{ 1, 2, 3 } = { 1, 3, 2 } = { 2, 1, 3 } = { 2, 3, 1 } = { 3, 1, 2 } = { 3, 2, 1 }
Ein Element kann nicht “mehrfach” in einer Menge auftreten.
Es ist entweder in der Menge, oder es ist nicht in der Menge.
Beispielsweise gilt:

Tags: Mengen Ordnung
Source:
Source:
Wie ist die Schreibweise für Element in einer Menge?
Wir schreiben a ∈ M, falls ein Element a in der Menge M
enthalten ist.
enthalten ist.
Tags: Element einer Menge
Source:
Source:
Wie ist die Schreibweise für Anzahl der Elemente einer Menge?
Für eine Menge M gibt | M | die Anzahl ihrer Elemente an.
Tags: Anzahl Elemente Menge
Source:
Source:
Wie ist die Schreibweise für die Teilmengenbeziehung?
Wir schreiben A ⊆ B, falls jedes Element von A auch in B
enthalten ist. Die Beziehung ⊆ heißt auch Inklusion.
enthalten ist. Die Beziehung ⊆ heißt auch Inklusion.
Tags: Teilmenge
Source:
Source:
Wie ist die Schreibweise für leere Menge und welche Eigenschaften besitzt sie?
Mit ∅ oder {} bezeichnet man die leere Menge. Sie enthält keine
Elemente und ist Teilmenge jeder anderen Menge.
Elemente und ist Teilmenge jeder anderen Menge.
Tags: Leere Menge
Source:
Source:
Wie ist die Schreibweise für die Vereinigung?
Die Vereinigung zweier Mengen A, B ist die Menge M, die alle
Elemente enthält, die in A oder B vorkommen. Man schreibt dafür
A ∪ B.
A ∪ B = x | x ∈ A oder x ∈ B
x | x ∈ A oder x ∈ B

Elemente enthält, die in A oder B vorkommen. Man schreibt dafür
A ∪ B.
A ∪ B =
 x | x ∈ A oder x ∈ B
x | x ∈ A oder x ∈ B

Tags: Vereinigung
Source:
Source:
Wie ist die Schreibweise für den Schnitt zweier Mengen?
Der Schnitt zweier Mengen A, B ist die Menge M, die die Element
enthält, die sowohl in A als auch in B vorkommen. Man schreibt
dafür A ∩ B.
A ∩ B =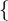 x | x ∈ A und x ∈ B
x | x ∈ A und x ∈ B 

enthält, die sowohl in A als auch in B vorkommen. Man schreibt
dafür A ∩ B.
A ∩ B =
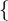 x | x ∈ A und x ∈ B
x | x ∈ A und x ∈ B 

Tags: Schnitt zweier Mengen
Source:
Source:
Wie ist die Schreibweise für die Mengendifferenz?
Seien A, B zwei Mengen. Dann bezeichnet A \ B die Menge aller
Elemente, die in A vorkommen und in B nicht vorkommen.
A \ B =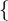 x | x ∈ A und x
x | x ∈ A und x 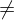 ∈ B }
∈ B }
Beispiele:
{ 0, 1, 2, 3, 4, 5 }\{ 0 } = { 1, 2, 3, 4, 5 }
{ a, b, c }\{ c, d } = { a, b }

Elemente, die in A vorkommen und in B nicht vorkommen.
A \ B =
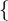 x | x ∈ A und x
x | x ∈ A und x 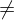 ∈ B }
∈ B }Beispiele:
{ 0, 1, 2, 3, 4, 5 }\{ 0 } = { 1, 2, 3, 4, 5 }
{ a, b, c }\{ c, d } = { a, b }

Tags: Mengendifferenz
Source:
Source:
Wie definiert man die Potenzmenge?
Die Menge P (M) ist die Menge aller Teilmengen von M.
Tags: Potenzmenge
Source:
Source:
Wie ist die Schreibweise der Potenzmenge und wie berechnet sich die Anzahl der Mengen einer Potenzmenge?
Sei M eine Menge. Die Menge P (M) ist die Menge aller
Teilmengen von M.
P (M) =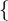 A | A ⊆ M
A | A ⊆ M 
Beispiel:
P ( { 1, 2, 3 } ) = {∅ , { 1 } , { 2 } , { 3 } , { 1, 2 } , { 1, 3 } , { 2, 3 } , { 1, 2, 3 }} .
Es gilt: (für eine endliche Menge M).
(für eine endliche Menge M).
Teilmengen von M.
P (M) =
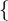 A | A ⊆ M
A | A ⊆ M 
Beispiel:
P ( { 1, 2, 3 } ) = {∅ , { 1 } , { 2 } , { 3 } , { 1, 2 } , { 1, 3 } , { 2, 3 } , { 1, 2, 3 }} .
Es gilt:
 (für eine endliche Menge M).
(für eine endliche Menge M).Tags: Potenzmenge
Source:
Source:
Wie ist die Schreibweise für das Kreuzprodukt und wie berechnet sich die Anzahl der Mengen eines Kreuzproduktes?
Seien A, B zwei Mengen. Die Menge A × B ist die Menge aller
Paare (a, b), wobei die erste Komponente des Paars aus A, die
zweite aus B kommt.
A × B =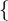 (a, b) | a ∈ A, b ∈ B
(a, b) | a ∈ A, b ∈ B 
Beispiel:
{ 1, 2 } × { 3, 4, 5 } = { (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5) }
Es gilt: | A × B | = | A | · | B | (für endliche Menge A, B).
Paare (a, b), wobei die erste Komponente des Paars aus A, die
zweite aus B kommt.
A × B =
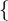 (a, b) | a ∈ A, b ∈ B
(a, b) | a ∈ A, b ∈ B 
Beispiel:
{ 1, 2 } × { 3, 4, 5 } = { (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5) }
Es gilt: | A × B | = | A | · | B | (für endliche Menge A, B).
Tags: Kreuzprodukt
Source: VL 2
Source: VL 2
Was ist eine Relation zweier Mengen?
Eine Teilmenge des Kreuzprodukts von der Menge A und der Menge B nennt man Relation zwischen A und B.
Tags: Relation
Source: VL 2
Source: VL 2
Welche 2 Schreibweisen gibt es, um zu zeigen, dass eine Relation zwischen Elementen zweier Mengen besteht?
Standardschreibweise: (2,b)∈R
Infix-Schreibweise: 2 R b
Infix-Schreibweise: 2 R b
Tags: Relation
Source: VL 2
Source: VL 2
Was ist eine Funktion der Menge A in die Menge B?
Es muss für eine Relation gelten:
Für jedes Element a∈ A gibt es genau ein Element b∈ B mit
(a,b) ∈ R
Für jedes Element a∈ A gibt es genau ein Element b∈ B mit
(a,b) ∈ R
Tags: Funktionen, Relationen
Source: VL 2
Source: VL 2
Wie schreibt man Funktionen auf?
f: A  B
B
 f(a)
f(a)
Die Funktion f bildet ein Element a ∈ A auf ein Element f (a) ∈ B ab. Dabeist A der Definitionsbereich und B der Wertebreich.
 B
B f(a)
f(a)Die Funktion f bildet ein Element a ∈ A auf ein Element f (a) ∈ B ab. Dabeist A der Definitionsbereich und B der Wertebreich.
Tags: Funktionen, Relationen
Source: VL 2
Source: VL 2
Was ist eine injektive Funktion?
Eine Funktion f: A  B heißt injenktiv, falls es keine Elemente a1, a2 ∈ A gibt mit a1
B heißt injenktiv, falls es keine Elemente a1, a2 ∈ A gibt mit a1 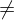 a2 und f(a1) = f(a2).
a2 und f(a1) = f(a2).
Mit anderen Worten: Auf kein Element im Wertebereich zeigt mehr als ein Pfeil.
 B heißt injenktiv, falls es keine Elemente a1, a2 ∈ A gibt mit a1
B heißt injenktiv, falls es keine Elemente a1, a2 ∈ A gibt mit a1 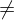 a2 und f(a1) = f(a2).
a2 und f(a1) = f(a2).Mit anderen Worten: Auf kein Element im Wertebereich zeigt mehr als ein Pfeil.
Tags: Funktionen, Relationen
Source: VL 2
Source: VL 2
Was ist eine surjektive Funktion?
Eine Funktion f: A  B heißt surjektiv, falls es für jedes b ∈ B (mindestens) ein a ∈ A gibt mit f(a) = B.
B heißt surjektiv, falls es für jedes b ∈ B (mindestens) ein a ∈ A gibt mit f(a) = B.
Mit anderen Worten: auf jedes Element im Wertebreich zeigt (mindestens) ein Pfeil.
 B heißt surjektiv, falls es für jedes b ∈ B (mindestens) ein a ∈ A gibt mit f(a) = B.
B heißt surjektiv, falls es für jedes b ∈ B (mindestens) ein a ∈ A gibt mit f(a) = B.Mit anderen Worten: auf jedes Element im Wertebreich zeigt (mindestens) ein Pfeil.
Tags: Funktionen, Relationen
Source: VL 2
Source: VL 2
Was ist eine bijektive Funktion? Welche besondere Eigenschaft hat sie?
Eine Funktion f:  heißt bijektiv, falls sie injektiv und surjektiv ist.
heißt bijektiv, falls sie injektiv und surjektiv ist.
Mit anderen Worten: auf jedes Element im Wertebereich zeigt genau ein Pfeil, d.h., es gibt eine eins-zu-eins-Zuordnung zwischen den Elementen des Definitionsbereichs und des Wertebereichs.
Die bijektiven Funktionen sind genau die invertierbaren
Funktionen. Zu einer bijektiven Funktion f : gibt es eine Umkehrfunktion
gibt es eine Umkehrfunktion 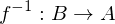 mit folgenden Eigenschaften:
mit folgenden Eigenschaften:
 (
( (a)) = a für alle a
(a)) = a für alle a  A
A
 (b)) = b für alle b
(b)) = b für alle b  B
B
 heißt bijektiv, falls sie injektiv und surjektiv ist.
heißt bijektiv, falls sie injektiv und surjektiv ist.Mit anderen Worten: auf jedes Element im Wertebereich zeigt genau ein Pfeil, d.h., es gibt eine eins-zu-eins-Zuordnung zwischen den Elementen des Definitionsbereichs und des Wertebereichs.
Die bijektiven Funktionen sind genau die invertierbaren
Funktionen. Zu einer bijektiven Funktion f :
 gibt es eine Umkehrfunktion
gibt es eine Umkehrfunktion 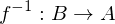 mit folgenden Eigenschaften:
mit folgenden Eigenschaften: (
( (a)) = a für alle a
(a)) = a für alle a  A
A (b)) = b für alle b
(b)) = b für alle b  B
BTags: Funktionen, Relationen
Source: VL 2
Source: VL 2
Wie notiert man eine Verknüpfung von Funktionen?
Wenn die Funktionen f:  und g:
und g:  gegeben sind, dann wird die Verknüpfung bzw. die Hintereinanderausführung mit
gegeben sind, dann wird die Verknüpfung bzw. die Hintereinanderausführung mit 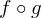 bezeichnet.
bezeichnet.

 und g:
und g:  gegeben sind, dann wird die Verknüpfung bzw. die Hintereinanderausführung mit
gegeben sind, dann wird die Verknüpfung bzw. die Hintereinanderausführung mit 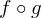 bezeichnet.
bezeichnet.
Tags: Funktionen, Relationen
Source: VL 2
Source: VL 2
Welche Bedingungen müssen für eine Äquivalenzrelation gegeben sein?
Bsp: R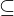 A x A
A x A
Bsp: R
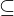 A x A
A x A1. Reflexivität: für alle a ∈ A gilt (a,a) ∈ R.
2. Transitivität: Falls für beliebige a,b,c ∈ A (a,b) ∈ R und (b,c) ∈R gilt, so muss auch (a,c) ∈ R gelten.
3. Symmetrie: Falls für beliebige a,b ∈ A (a,b) ∈ R gilt, so muss auch (b,a) ∈ R gelten.
2. Transitivität: Falls für beliebige a,b,c ∈ A (a,b) ∈ R und (b,c) ∈R gilt, so muss auch (a,c) ∈ R gelten.
3. Symmetrie: Falls für beliebige a,b ∈ A (a,b) ∈ R gilt, so muss auch (b,a) ∈ R gelten.
Tags: Relationen
Source: VL 2
Source: VL 2
Gegeben ist die Funktion f:  und
und 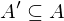 . Gib das Bild und das Urblild an!
. Gib das Bild und das Urblild an!
 und
und 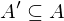 . Gib das Bild und das Urblild an!
. Gib das Bild und das Urblild an!Das Bild von A' unter der Funktion f, wenn 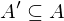 :
:
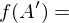 {
{  }
}
Das Urbild von B' unter der Funktion f, wenn :
:
 {
{  }
}
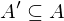 :
: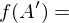 {
{  }
}Das Urbild von B' unter der Funktion f, wenn
 :
: {
{  }
}Tags: Funktionen, Relationen
Source: VL 2
Source: VL 2
Was ist Teilbarkeit? Definiere.
Die Relation Teilbarkeit (senkrechter Strich | ) ist eine partielle Ordnung, wenn man sie auf die natürlichen Zahlen einschränkt.
Definition:
Seien a, b
 zwei ganze Zahlen.
zwei ganze Zahlen.
Man sagt, a teilt b wenn es ein z
 gibt mit a * z = b.
gibt mit a * z = b.
Wir schreiben auch a | b und nennen a Teiler von b
Definition:
Seien a, b

 zwei ganze Zahlen.
zwei ganze Zahlen.Man sagt, a teilt b wenn es ein z

 gibt mit a * z = b.
gibt mit a * z = b.Wir schreiben auch a | b und nennen a Teiler von b
Tags: Grundlagen - Zahlen
Source:
Source:
Welche Beziehungen gelten und was käme für "z" raus, wenn gilt a | b und a * z = b?
2 | 18
-7 | 14
3 | 10
0 | 0
0 | 7
7 | 0
2 | 18
-7 | 14
3 | 10
0 | 0
0 | 7
7 | 0
2 | 18 gilt, z = 9
-7 | 14 gilt, z = -2
3 | 10 gilt nicht
0 | 0 gilt, z ist beliebig
0 | 7 gilt nicht
7 | 0 gilt, z = 0
Merk dir das: rechts darf immer die Null stehen, links nie (es sei denn, sie steht rechts auch)
-7 | 14 gilt, z = -2
3 | 10 gilt nicht
0 | 0 gilt, z ist beliebig
0 | 7 gilt nicht
7 | 0 gilt, z = 0
Merk dir das: rechts darf immer die Null stehen, links nie (es sei denn, sie steht rechts auch)
Tags: Grundlagen - Zahlen, VL vom 4.5.10
Source:
Source:
Was ist eine Primzahl? Definiere.
Eine Zahl p 
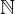 0 heißt Prinzahl, wenn folgendes gilt:
0 heißt Prinzahl, wenn folgendes gilt:
p 0 und p
0 und p  1
1
Die einzigen Teiler von p in den natürlichen Zahlen sind 1 und p selbst.
(Es gibt unendlich viele Primzahlen. Die ersten sind
2, 3, 5, 7, 11, 13, 17, 19, 23)

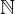 0 heißt Prinzahl, wenn folgendes gilt:
0 heißt Prinzahl, wenn folgendes gilt:p
 0 und p
0 und p  1
1Die einzigen Teiler von p in den natürlichen Zahlen sind 1 und p selbst.
(Es gibt unendlich viele Primzahlen. Die ersten sind
2, 3, 5, 7, 11, 13, 17, 19, 23)
Tags: Zahlen 04.05.10
Source:
Source:
Erkläre die Primfaktorzerlegung
Sei n eine natürliche Zahl mit n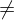 0.
0.
Ein Produkt von Primzahlen = n heißt Primfaktorzerlegung von n.
= n heißt Primfaktorzerlegung von n.
Jede Zahl n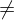 0 besitzt eine solche Primfaktorzerlegung.
0 besitzt eine solche Primfaktorzerlegung.
Wenn man zudem verlangt, dass die Primzahlen in aufsteigender Reihenfolge angeordnet sind, dann ist die Primfaktorzerlegung einer Zahl eindeutig.
Bsp: 55=5*11
Achtung: Die Primfaktorzerlegung von 1 ist das leere Produkt.
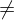 0.
0.Ein Produkt von Primzahlen
 = n heißt Primfaktorzerlegung von n.
= n heißt Primfaktorzerlegung von n.Jede Zahl n
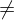 0 besitzt eine solche Primfaktorzerlegung.
0 besitzt eine solche Primfaktorzerlegung.Wenn man zudem verlangt, dass die Primzahlen in aufsteigender Reihenfolge angeordnet sind, dann ist die Primfaktorzerlegung einer Zahl eindeutig.
Bsp: 55=5*11
Achtung: Die Primfaktorzerlegung von 1 ist das leere Produkt.
Tags: VL vom 4.5.10
Source:
Source:
Was ist d 
 wenn folgendes gilt:
wenn folgendes gilt:
d | a und d | b
und für jede andere Zahl d', die a und b teilt, gilt d'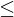 d
d

 wenn folgendes gilt:
wenn folgendes gilt:d | a und d | b
und für jede andere Zahl d', die a und b teilt, gilt d'
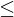 d
dKomplizierte Frage - simple Antwort:
Dann ist d natürlich der größte gemeinsame Teiler von a und b.
Also:
d = ggT(a,b)
Dann ist d natürlich der größte gemeinsame Teiler von a und b.
Also:
d = ggT(a,b)
Tags: VL vom 4.5.10
Source:
Source:
Die drei Regeln der Methode zur Errechnung des ggT von a und b
-> ggT(0,a) = a
-> ggT(a,b) = ggT(b,a)
-> falls a größer oder gleich b ist: ggT(a,b) = ggT(a-b,b)
auf Deutsch:
>>> Die beiden Zahlen kann man immer tauschen.
>>> Wenn links die größere (oder gleiche) steht, zieht man die kleinere von ihr ab.
Das alles macht man so lange, bis man links eine 0 stehen hat, die rechte Zahl ist dann das Ergebnis (vgl. Regel 1)
-> ggT(a,b) = ggT(b,a)
-> falls a größer oder gleich b ist: ggT(a,b) = ggT(a-b,b)
auf Deutsch:
>>> Die beiden Zahlen kann man immer tauschen.
>>> Wenn links die größere (oder gleiche) steht, zieht man die kleinere von ihr ab.
Das alles macht man so lange, bis man links eine 0 stehen hat, die rechte Zahl ist dann das Ergebnis (vgl. Regel 1)
Tags: VL vom 4.5.10
Source:
Source:
Errechne den ggT von 132 und 88 nach der erlernten Methode ohne Taschenrechner.
ggT(132,88) = ggT(44,88) = ggT(88,44) = ggT(44,44) = ggT(0,44) = 44
Tags: VL vom 4.5.10
Source:
Source:
Was ist m 
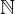 0 mit m
0 mit m 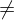 0 wenn folgendes gilt:
0 wenn folgendes gilt:
a | m und b | m (bei a, b
 )
)
und
für jede andere natürliche Zahl m', die von a und b geteilt wird, gilt: m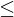 m'.
m'.

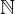 0 mit m
0 mit m 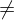 0 wenn folgendes gilt:
0 wenn folgendes gilt:a | m und b | m (bei a, b

 )
)und
für jede andere natürliche Zahl m', die von a und b geteilt wird, gilt: m
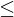 m'.
m'.Dann ist m das kleinste gemeinse Vielfache von a und b, also:
m = kgV(a,b)
m = kgV(a,b)
Tags: VL vom 4.5.10
Source:
Source:
Bei der Berechnung des ggT: wie kann man die 3. Regel
-> falls a größer oder gleich b ist: ggT(a,b) = ggT(a-b,b)
anders ausdrücken?
-> falls a größer oder gleich b ist: ggT(a,b) = ggT(a-b,b)
anders ausdrücken?
ggT(a,b) = ggT(a mod b, b)
bei a >= b
bei a >= b
Tags: VL vom 4.5.10
Source:
Source:
Was muss gelten damit die diophantische Gleichung
a*x + b*y = c
genau eine Lösung hat?
a*x + b*y = c
genau eine Lösung hat?
Die Gleichung hat genau eine Lösung, wenn gilt
ggT(a,b) | c
Also muss der ggT von a und b Teiler von c sein.
(Auch wenn das noch nicht die Lösung der Gleichung ist)
ggT(a,b) | c
Also muss der ggT von a und b Teiler von c sein.
(Auch wenn das noch nicht die Lösung der Gleichung ist)
Tags: VL vom 4.5.10
Source:
Source:
Wann heißt eine Zahl teilerfremd?
Zwei natürliche Zahlen (inkl. Null) heißten teilerfremd, falls
ihr ggT 1 ist:
ggT(a,b) = 1 ==> a und b sind teilerfremd
ihr ggT 1 ist:
ggT(a,b) = 1 ==> a und b sind teilerfremd
Tags: VL vom 4.5.10
Source:
Source:
Wie ist die Eulersche 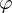 -Funktion (Phi-Fkt.) definiert?
-Funktion (Phi-Fkt.) definiert?
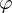 -Funktion (Phi-Fkt.) definiert?
-Funktion (Phi-Fkt.) definiert?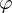 (n) mit n
(n) mit n 
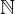 0 ist die Anzahl der Zahlen zwischen 1 und n, die zu n teilerfremd sind.
0 ist die Anzahl der Zahlen zwischen 1 und n, die zu n teilerfremd sind.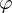 (n) = | { m
(n) = | { m 
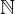 0
0  1
1 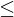 m
m 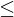 n und ggT(m,n) = 1 } |
n und ggT(m,n) = 1 } |Tags: VL vom 4.5.10
Source:
Source:
Wie ist ein Monoid definiert?
Gegeben sei eine Menge M und eine zweistellige Abbildung
 : M x M
: M x M  M. Wir benutzen meist die Infix-Schreibweise:
M. Wir benutzen meist die Infix-Schreibweise:
 (m
(m , m
, m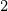 ) = m
) = m
 m
m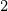 und bezeichnen
und bezeichnen  als zweistelligen Operator.
als zweistelligen Operator.
(M, ) heißt Monoid, falls folgendes gilt:
) heißt Monoid, falls folgendes gilt:
- ist assoziativ, d.h., es gilt m
ist assoziativ, d.h., es gilt m
 (m
(m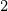
 m
m ) = (m
) = (m
 m
m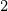 )
)  m
m
für alle m , m
, m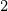 , m
, m
 M.
M.
- Es gibt ein neutrales Element e M, für das gilt:
M, für das gilt:
e m = m
m = m  e = m für alle m
e = m für alle m  M.
M.
 : M x M
: M x M  M. Wir benutzen meist die Infix-Schreibweise:
M. Wir benutzen meist die Infix-Schreibweise: (m
(m , m
, m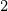 ) = m
) = m
 m
m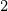 und bezeichnen
und bezeichnen  als zweistelligen Operator.
als zweistelligen Operator.(M,
 ) heißt Monoid, falls folgendes gilt:
) heißt Monoid, falls folgendes gilt:-
 ist assoziativ, d.h., es gilt m
ist assoziativ, d.h., es gilt m
 (m
(m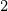
 m
m ) = (m
) = (m
 m
m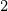 )
)  m
m
für alle m
 , m
, m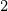 , m
, m
 M.
M.- Es gibt ein neutrales Element e
 M, für das gilt:
M, für das gilt:e
 m = m
m = m  e = m für alle m
e = m für alle m  M.
M.Tags: Algebraische Strukturen, VL 18.05.
Source:
Source:
Wie ist die Kurzschreibweise für Modulo-Rechnen und welche Modulo-Gesetze gibt es?
Wir denieren 
 =
= 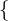 0, 1, ..., n - 1
0, 1, ..., n - 1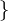 mit folgender Addition +
mit folgender Addition +
und Multiplikation
 . Seien k,
. Seien k, 
 Z
Z , dann gilt:
, dann gilt:
k +
 = (k +
= (k +  ) mod n
) mod n
k

 = (k
= (k 
 ) mod n
) mod n
(
 ,+
,+ ) und (
) und (
 ,
, 
 ) sind Monoide
) sind Monoide
(mit neutralen Elementen 0 bzw. 1)
Modulo-Gesetze
(a + b) mod n = ((a mod n) + (b mod n)) mod n
(a b) mod n = ((a mod n)
b) mod n = ((a mod n)  (b mod n)) mod n
(b mod n)) mod n
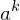 mod n =
mod n = 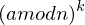 mod n
mod n

 =
= 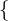 0, 1, ..., n - 1
0, 1, ..., n - 1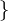 mit folgender Addition +
mit folgender Addition +
und Multiplikation

 . Seien k,
. Seien k, 
 Z
Z , dann gilt:
, dann gilt:k +

 = (k +
= (k +  ) mod n
) mod nk


 = (k
= (k 
 ) mod n
) mod n(

 ,+
,+ ) und (
) und (
 ,
, 
 ) sind Monoide
) sind Monoide(mit neutralen Elementen 0 bzw. 1)
Modulo-Gesetze
(a + b) mod n = ((a mod n) + (b mod n)) mod n
(a
 b) mod n = ((a mod n)
b) mod n = ((a mod n)  (b mod n)) mod n
(b mod n)) mod n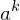 mod n =
mod n = 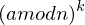 mod n
mod nTags: Algebraische Strukturen, VL 18.05.
Source:
Source:
Wie ist eine Gruppe definiert?
Ein Monoid 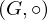 mit neutralem Element e heißt Gruppe, wenn zusätzlich zu den Monoid-Eigenschaften noch folgendes gilt:
mit neutralem Element e heißt Gruppe, wenn zusätzlich zu den Monoid-Eigenschaften noch folgendes gilt:
Für jedes gibt es ein
gibt es ein 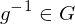 mit
mit  .
.
Dabei heißt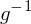 das Inverse von
das Inverse von 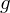 .
.
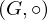 heißt kommutative Gruppe (oder abelsche Gruppe), falls außerdem
heißt kommutative Gruppe (oder abelsche Gruppe), falls außerdem  für alle
für alle  gilt.
gilt.
Bemerkung: In jeder Gruppe gilt nicht nur , sondern auch
, sondern auch 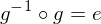 für alle
für alle  .
.
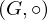 mit neutralem Element e heißt Gruppe, wenn zusätzlich zu den Monoid-Eigenschaften noch folgendes gilt:
mit neutralem Element e heißt Gruppe, wenn zusätzlich zu den Monoid-Eigenschaften noch folgendes gilt:Für jedes
 gibt es ein
gibt es ein 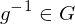 mit
mit  .
.Dabei heißt
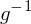 das Inverse von
das Inverse von 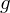 .
.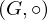 heißt kommutative Gruppe (oder abelsche Gruppe), falls außerdem
heißt kommutative Gruppe (oder abelsche Gruppe), falls außerdem  für alle
für alle  gilt.
gilt.Bemerkung: In jeder Gruppe gilt nicht nur
 , sondern auch
, sondern auch 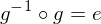 für alle
für alle  .
.Tags: Algebraische Strukturen, VL 18.05.
Source:
Source:
Tags: Algebraische Strukturen, VL 18.05.
Source:
Source:
Existieren in ( \
\ ) alle multiplikativen Inversen, wenn n keine Primzahl ist?
) alle multiplikativen Inversen, wenn n keine Primzahl ist?
 \
\ ) alle multiplikativen Inversen, wenn n keine Primzahl ist?
) alle multiplikativen Inversen, wenn n keine Primzahl ist?Nein.
Erläuterung s. Vorlesung.
Erläuterung s. Vorlesung.
Tags: Algebraische Strukturen, VL 18.05.
Source:
Source:
Tags: Algebraische Strukturen, VL 18.05.
Source:
Source:
Was sind Körper und welche Axiome gelten für Sie? Nenne je win Beispiel und ein Gegenbeipiel für Körper!




Tags: Algebraische Strukturen, VL 18.05.
Source:
Source:
Tags: Algebraische Strukturen, VL 18.05.
Source:
Source:
Flashcard set info:
Author: P-H-I-L
Main topic: Mathematik
Topic: Mathematische Strukturen
Published: 13.04.2010
Card tags:
All cards (50)
Äquivalenzklasse (1)
Funktionen (7)
Grundlagen (1)
Kreuzprodukt (1)
Leere Menge (1)
Mengen Ordnung (1)
Mengendifferenz (1)
Potenzmenge (2)
Relation (2)
Relationen (8)
Teilmenge (1)
Vereinigung (1)
VL 18.05. (10)
VL vom 4.5.10 (10)
Zahlen 04.05.10 (1)













