Was ist ein Histogramm?
- Histogramme sind Verteilungen von Pixelintensitäten
- keine räumlichen Informationen
- statistisch gesehen Dichteverteilungen
- Die Anzahl der Bins hängt von der Quantisierung und vom Farbraum ab.
absolute Histogramme
- rotationsinvariant
- translationsinvariant
relative Histogramme => Anzahl Elemente in Bin durch Gesamtanzahl => Wertebereich [0..1] => Wahrscheinlichkeiten
- rotationsinvariant
- translationsinvariant
- skalierungsinvariant
Was für Histogrammarten kennen Sie im Bezug auf Farbbilder?
- Luminanz-Histogramm (Histogramm des Korrespondierenden Grauwertbildes (nur Helligkeiten) ... z.B. L (Luminanz) ab
- Histogramm der einzelnen Farbkomponenten
- kumulatives Histogramm
- 3D-Histogramm (RGB) => 1D (Binning, zusammenfassen kleiner 3D-Würfel)
- 3D-Histogramm => 2D-Farbhistogramme (Projektionen des 3D-RGB-Farbwürfels)
- 3D-Histogramme (zu Speicheraufwändig)
Fabrqauntisierung => Farben mit gewissem Farbabstand werden zu/in einem Bin zusammengefasst
Welche Abstandsmaße für Histogramme kennen Sie?
Sum of Squared Differences
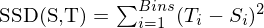
Minkowski-Abstand
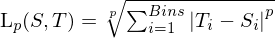
Histogrammschnitt
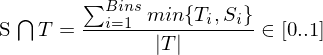
Chi-Square-Test (statistisch)
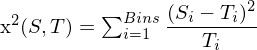
Kullback-Leibler-Divergenz
Earth-Movers-Distance
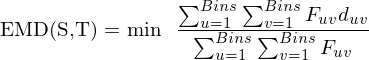
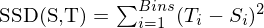
- es entstehen hohe Abstände .. entspricht nicht der menschlichen Farbwahrnehmung
Minkowski-Abstand
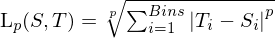
-
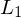 = Absolute-Distanz / Manhatten-Distanz
= Absolute-Distanz / Manhatten-Distanz -
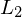 = Euklidische Distanz
= Euklidische Distanz - Einfluss der Differenz wird durch größere p verringert
Histogrammschnitt
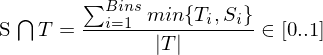
- heuristisches Abstandsmaß
- Verallgemeinerung der
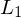 -Distanz
-Distanz - Ergebnis = 1 => vollkommene Übereinstimmung
Chi-Square-Test (statistisch)
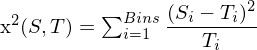
- kleine Werte bedeuten geringen Abstand
- Beste Ergebnisse in Bezug auf Rauschen, Unschärfe und Bildrotation
Kullback-Leibler-Divergenz
- aus Informationstheorie
Earth-Movers-Distance
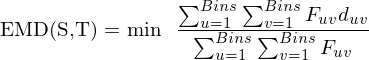
- man berechnet die Anzahl der Pixel, die Arbeit (F) und den Weg bzw. die Distanz (d) der Bins zueinander um
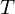 in
in 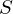 zu überführen => Transportproblem (geringsten Aufwand finden)
zu überführen => Transportproblem (geringsten Aufwand finden) - T ist der Erdhügel und S stellt die zu Löcher dar, die möglichst effizient gefüllt werden sollen
- ist ein Suchproblem: kann mit A* oder dem Ungarischen Algorithmus gelöst werden
- entspricht eher dem Farbunterschied der menschlichen Wahrnehmung
Wie würde man vorgehen wenn man in einem Farbbild ein Objekt suchen würde? (ohne Histogrammrückprojektion)
Durch einen Histogrammvergleich (siehe Abstandsmaße)!
1. Von dem gesuchten Modell (roter Stift) wird eine binäre Maske M erstellt (Differenzbildverfahren).
2. Modell-Histogramm T mit Hilfe der Maske berechnen (nur Modell-Pixel dürfen in das Modell-Histogramm einfließen, z.B. mehrere Ansichten)
3. Bestimmen der Größe des Sliding-Windows (Größe des Fensters - ist ausschlaggebend für den Erfolg
4. Für jedes Teilbild Histogramm berechnen und mit dem Modell-Histogramm Vergleichen: (Sum of Square Differences, Minkowski-Abstand (absolute oder euklidische Distanz), Earth Mover’s Distance, Chi-Square Test, Kullback-Leibler-Divergenz)
1. Von dem gesuchten Modell (roter Stift) wird eine binäre Maske M erstellt (Differenzbildverfahren).
2. Modell-Histogramm T mit Hilfe der Maske berechnen (nur Modell-Pixel dürfen in das Modell-Histogramm einfließen, z.B. mehrere Ansichten)
3. Bestimmen der Größe des Sliding-Windows (Größe des Fensters - ist ausschlaggebend für den Erfolg
4. Für jedes Teilbild Histogramm berechnen und mit dem Modell-Histogramm Vergleichen: (Sum of Square Differences, Minkowski-Abstand (absolute oder euklidische Distanz), Earth Mover’s Distance, Chi-Square Test, Kullback-Leibler-Divergenz)
Wie funktioniert die Histogrammrückprojektion?
Histogrammrückprojektion:

Interpretation:
- Von dem gesuchten Modell (roter Stift) wird eine binäre Maske M erstellt (Differenzbildverfahren).
- Modell-Histogramm T mit Hilfe der Maske berechnen (nur Modell-Pixel dürfen in das Modell-Histogramm einfließen)
- Histogramm S aus dem Szenenbild A berechnen
- Verhältnishistogramm Q = T/S berechnen (Werte von Q liegen zw. 0 und 1 =>

- Rückprojektion des Verhälnishistogramm Q in das Szenenbild A: Ergebnis ist AQ + das gesuchte Objekt befindet sich an einem der Orte, wo in AQ hohe Werte stehen

Interpretation:
- [1] Farbe in Szene und Modell im gleichen Verhältnis vertreten, d.h. Orte mit dieser Farbe im Szenenbild A sind mit höherer Wahrscheinlichkeit mögliche Orte des Modells
- [2] Farbe ist in Szene verhältnismäßig oft vertreten, im Modell weniger, d.h. geringere Wahrscheinlichkeit, dass an diesen Orten das Modell tatsächlich zu finden ist
- [3] Farbe des Modells in der Szene überhaupt nicht vorhanden, muss also bei der Rückprojektion nicht beachtet werden (Abfangen der Division durch Null)
- [4] Farbe ist in Szene verhältnismäßig selten vertreten, d.h. Orte mit dieser Farbe im Szenenbild A sind mit hoher Wahrscheinlichkeit mögliche Orte des Modells (Wahrscheinlickeitswert wird auf 1 geclampt)
- Die tatsächliche Position des Objekts wird mittels Faltung von AQ mit M ermittelt (Ergebnis AQ*M), da so neben Farbinformationen des Objekts auch dessen Form beachtet wird
- Position des Objekts ist an der Stelle des Maximalwerts in AQ*M
Was passiert denn nun, wenn ich im Szenehistogramm weniger Bins habe? (Histogrammrückprojektion)
Dieser Bin wird dann nicht rückprojeziert (bzw. auf Null gesetzt, Division durch 0 beachten).
Oder Quantisierungsstufen bzw. Binanzahl im Modellhistogramm T an Binanzahl im Szenehistogramm angleichen.
Oder Quantisierungsstufen bzw. Binanzahl im Modellhistogramm T an Binanzahl im Szenehistogramm angleichen.
Wie kann man sie lösen?
- Kostenfunktion der EMD kann möglichst beleuchtungsinvariant sein.
- (Statistische Abstandsmaße kommen damit zurecht <- Antwort Trierscheidt)
- Farbnormalisierung: Gray World Assumption, CCN, Rotation im RGB-Farbraum
- Bild in einen anderen Farbraum umrechnen, der zwischen Farbe und Luminanz trennt (YUV, L*a*b*/L*u*v). Die Luminanz darf in den Farbraum nicht einbezogen werden
Was ist Farbkonstanz überhaupt?
Der Effekt, dass ein Mensch eine Farbe als gleich empfindet, auch wenn sie unterschiedlich beleuchtet ist. Beispiel:

Farbe in B ist exakt die gleiche wie in A (geprüft mit Photoshop), aber weil B im Schatten liegt, ändert der menschliche Sehapparat die Empfindung der Farbe aufgrund der Umgebungsbedingungen.
Ein CCD-Chip kann dies nicht!
In der BV möchte man auf das Erkennungsmerkmal Farbe nicht verzichten, da es invariant gegenüber Rotation, Translation und Skalierung eines Objektes in der Szene ist.
Durch Farbnormierungs-Algorithmen versucht man einen gewissen Grad an Farbkonstanz anzunähern (100% nicht möglich). Nach der Normierung sollen die Bilder invariant gegenüber Beleuchtungsänderungen sein. Die Normalisierung soll ohne Vorwissen erfolgen, also nur datengetrieben.

Farbe in B ist exakt die gleiche wie in A (geprüft mit Photoshop), aber weil B im Schatten liegt, ändert der menschliche Sehapparat die Empfindung der Farbe aufgrund der Umgebungsbedingungen.
Ein CCD-Chip kann dies nicht!
In der BV möchte man auf das Erkennungsmerkmal Farbe nicht verzichten, da es invariant gegenüber Rotation, Translation und Skalierung eines Objektes in der Szene ist.
Durch Farbnormierungs-Algorithmen versucht man einen gewissen Grad an Farbkonstanz anzunähern (100% nicht möglich). Nach der Normierung sollen die Bilder invariant gegenüber Beleuchtungsänderungen sein. Die Normalisierung soll ohne Vorwissen erfolgen, also nur datengetrieben.
Welche Algorithmen zur Farbnormalisierung kennen Sie?
Global (Annahme: einheitliche Beleuchtung in Szene):
Lokal (unterschiedliche Beleuchtungssituationen in einer Szene):
- Gray-World-Assumption
- Comprehensive-Color-Normalization
- Rotation im RGB-Farbraum
Lokal (unterschiedliche Beleuchtungssituationen in einer Szene):
- Local space average color: Durchschnittliche lokale Farbe (Anwendung Graue-Welt-Hypothese lokal (z.B. Gaussfunktion))
- Retinex-Algorithmus
- Comprehensive local space average color
Was ist die Gray-World-Assumption und wie funktioniert sie?

Wenn keine Annahme über die Farben in einem Bild getroffen werden kann, geht man davon aus, dass sich die Farbwerte in einem Bild vektoriell zu Grau addieren, dass also das Bild im Mittel Grau ist. Wenn das in einem Bild nicht der Fall ist, geht man davon aus, dass das auf farbige Beleuchtung zurückzuführen ist und normiert das Bild so, dass die Graue-Welt-Annahme erfüllt ist.
Normalisierung aller Farbkanäle mit einem Skalierungsfaktor pro Farbkanal, so dass der Mittelwert jedes Kanals 128 ist (-> Mittelwert des gesamten Bilds wird grau -> Farbstiche werden herausgerechnet)
Algorithmus:
1. Mittelwerte der einzelnen Farbkanäle berechnen (r',g',b')
2. globalen Mittelwert bestimmen rgb = (r'+g'+b')/3
3. Skalierungsfaktor für jeden Kanal bestimmen r'' = rgb/r', ...
4. Skalierung der Originalwerte jedes Farbkanals
=> Mittelwert Bildes danach (128,128,128)^T
Voraussetzung: Verschiedene Farben in Bild vorhanden => sonst bei Bild mit Banane (viel Gelb) => danach grau
Wie funktioniert Comprehensive Color Normalization (CCN)?

Comprehensive Color Normalization (CCN): Besteht aus zwei iterativ wiederholbaren Schritten, die konvergieren (meistens 5 Iterationen)
1.) Herausrechnen der lokalen Intensitätsschwankungen, durch Normalisierung der Farbkomponenten jedes Pixels auf die Summe 1
2.) Anwenden der Gray World Assumption: Globale Normalisierung der Farbkanäle auf den Mittelwert (128, 128, 128)T
Algorithmus konvergiert immer!
Erzeugt Falschfarben.
Color-Cluster-Rotation ... bzw. Farbnormierung durch Rotation .. wie funktioniert das?
- Annahme: Graue-Welt-Hypothese
- Vorteil: original Helligkeit bleibt erhalten

1.Verschieben des Clusterzentrums (Mittelwert des Bildes) in den Ursprung des Würfels
2. Berechnung der Hauptachse durch die Principal Component Analysis (Skalierung und Normierung von Varianz)
3. Berechnung des Winkels und der Rotationsachse zwischen Grauachse und Hauptachse
4. Rotation des Clusters um die berechnete Rotationsachse und den Winkel
5. Verschieben des Clusters auf den Mittelpunkt der Unbuntachse (Gray World Assumption ist erfüllt)
6. Skalieren des Clusters entlang der Unbuntachse, um den Farbraum soweit als möglich auszunutzen
- Vorteil: original Helligkeit bleibt erhalten

1.Verschieben des Clusterzentrums (Mittelwert des Bildes) in den Ursprung des Würfels
2. Berechnung der Hauptachse durch die Principal Component Analysis (Skalierung und Normierung von Varianz)
3. Berechnung des Winkels und der Rotationsachse zwischen Grauachse und Hauptachse
4. Rotation des Clusters um die berechnete Rotationsachse und den Winkel
5. Verschieben des Clusters auf den Mittelpunkt der Unbuntachse (Gray World Assumption ist erfüllt)
6. Skalieren des Clusters entlang der Unbuntachse, um den Farbraum soweit als möglich auszunutzen
Wie werden die Farben eigentlich im Rechner repräsentiert?
Durch Farbräume.
Für unterschiedliche Farbräume existieren unterschiedliche Farbabstandsmaße.
In uniformen Farbräumen ensprechen gleiche euklidische Abstände im 3D-Farbraum empfindungsgemäß gleichen Farbunterschieden / Farbabständen (siehe L*a*b und L*u*v).
Geräteunabhängigkeit bedeutet, dass die Farben unabhängig von Art ihrer Erzeugung und Wiedergabetechnik definiert werden.
Sie speichern / kodieren die
Luminanz => Helligkeit
Chrominanz => Farblichkeit (kann abhängig oder unabhängig sein)
Chromazität setzt sich aus Farbton (Wellenlänge des monochromatischen Lichts eines Farbtons) und der Sättigung (relative Reinheit einer Farbe) zusammen.
Für unterschiedliche Farbräume existieren unterschiedliche Farbabstandsmaße.
In uniformen Farbräumen ensprechen gleiche euklidische Abstände im 3D-Farbraum empfindungsgemäß gleichen Farbunterschieden / Farbabständen (siehe L*a*b und L*u*v).
Geräteunabhängigkeit bedeutet, dass die Farben unabhängig von Art ihrer Erzeugung und Wiedergabetechnik definiert werden.
Sie speichern / kodieren die
Luminanz => Helligkeit
Chrominanz => Farblichkeit (kann abhängig oder unabhängig sein)
Chromazität setzt sich aus Farbton (Wellenlänge des monochromatischen Lichts eines Farbtons) und der Sättigung (relative Reinheit einer Farbe) zusammen.
Erklären Sie den XYZ-Farbraum bzw. das CIE-Normvalenzsystem.

XYZ = CIE Normvalenzsystem:
- Basiert auf der physiologischen Farbwahrnehmung des Menschen (der Zapfen), also den Mischverhältnissen der drei Grundfarben Rot (Long), Grün (Middle) und Blau (Short), dem Tristimulus, um die Farbwahrnehmung des Menschen nachzustellen (des CIE-Standard-Betrachters) ... ermittelt aus vielen Experimenten (mit 3 Projektoren)
- Der Farbraum wird als 2D CIE-Normfarbtafel dargestellt, dies wird durch die Normalisierung x + y + z = 1 erreicht.
- Diese Normalisierung hat zur Folge, dass Farben verschiedener Helligkeit nicht-linear auf ein und die selbse xy-Koordinate abgebildet werden.
- dabei wird die Y-Achse (Helligkeit in XYZ) auf eins abgebildet und dieser Schnitt im 3D-XYZ-Farbraum, dem "Zuckerhut", ergibt die "Schuhsole"
- X und Z beschreiben die Farbigkeit
CIE-Normfarbtafel mit x und y-Achse.
z ergibt sich aus x+y+z=1
Das Hufeisen der sichtbaren Farben wird begrenzt durch die Spektralfarblinie (380nm-780nm) und die Purpurlinie. W ist der Unbuntpunkt. Auf allen Strecken zwischen einer Spektralfarblinie und dem Unbuntpunkt verändert sich nicht die Farbe, sondern nur die Sättigung.
Im Inneren findet sich das Farbdreieck, was Monitore etc. darstellen können (Gamut).
XYZ ist nicht linear, da Farbänderungen in verschiedenen Bereichen des Farbraums größere oder kleinere euklidische Abstände zur Vergleichsfarbe benötigen.
Daher Entwicklung von Lab und Luv XYZ dient als Referenz für Umrechnung zwischen Farbräumen.
Angenommen wir nutzen jetzt XYZ und haben Y, die Helligkeit, weggeschmissen, also einen 2-dimensionalen Frabraum. Was macht man dann damit?
- da Farbabstände nicht gleich sind bzw. nicht der Farbwahrnehmung des Menschen entsprechen kann man die Werte in einen uniformen Farbraum transformieren ... L*a*b* oder L*u*v*
- Clustern um ihn mit einem 1D-Histogramm abbbilden zu können.
Wo steckt in der CIE-Normfarbtafel (Schuhsohle) denn schwarz?
Gibt's nur in XYZ (unnormiert), wenn alle drei Strahler auf 0 sind. (0, 0, 0) lässt sich aber nicht normalisieren (Division durch 0) und taucht daher nicht im normierten xyz auf.
CIE-Normfarbtafel ist aber ein Schnitt bei Y=1 ... also Helligkeit nicht gleich 0 => kein Schwarz ... Schwarz wäre bei XYZ = (0,0,0)
CIE-Normfarbtafel ist aber ein Schnitt bei Y=1 ... also Helligkeit nicht gleich 0 => kein Schwarz ... Schwarz wäre bei XYZ = (0,0,0)
Wie ist der RGB-Farbraum definiert? ... welche Eigenschaften hat er?

Die Entstehung von RGB war technisch motiviert. Der Farbraum wird für Monitore und Farbkameras verwendet.
Auf der Hauptdiagonalen des RGB-Würfels befindet sich die Unbunt-Achse, also die Grauwerte.
Im RGB-Farbraum sind nicht alle Farbvalenzen enthalten: insbesondere Spektralfarben erfordern negative Wiedergabeanteile, das entsprächnd fehlende Licht.
Wie ist der L*a*b*-Farbraum definiert? ... welche Eigenschaften hat er?

Die Skalen der a*-Achse und der b*-Achse umfassen einen Zahlenbereich von -150 bis +100 und -100 bis +150, ungeachtet dessen, dass es für einige Werte keine wahrnehmbare Entsprechung gibt.
L = Luminanz (Helligkeit)
a = Chrominanz (G(-)-R(+))
b = Chrominanz (B(-)-Y(+))
Farbraum basiert auf dem XYZ-Farbraum und damit auf der physiologischen Farbwahrnehmung des Menschen. Ist uniform und ermöglichen die mathematische Abstandsmessung zwischen Farben entspricht menschlicher Farbwahrnehmung.
Abstandsmaße:
• Euklidisch
• Polarkoordinaten
Vorteil L*a*b* der Weißpunkt (Xw, Yw, Zw) wird eingerechnet (Chromatische Adaption/Weißabgleich wird beachtet)
Nichtlineare Umrechnung zu RGB
Wie ist der L*u*v*-Farbraum definiert? ... welche Eigenschaften hat er?

L = Luminanz
u = Chrominanz (G(-) -R(+))
v = Chrominanz (B(-) -Y(+))
Farbraum stellt Erweiterungen des XYZ-Farbraums dar. Beide sind uniforme Farbräume, d.h. gleiche wahrgenommene Farbunterschiede haben gleiche Abstände im Diagramm.
Vorteil L*u*v* Mischfarben liegen auf der Geraden zwischen den zwei zu mischenden Spektralfarben.
Nichtlineare Umrechnung zu RGB
Wie ist der YUV-Farbraum definiert? ... welche Eigenschaften hat er?

Y = Luminanz (Helligkeit aus XYZ-Farbraum)
U = Chrominanz (Gelb/Grün -> Blau)
V = Chrominanz (Gelb/Grün -> Rot)
YUV wird in der Video- und Fernsehtechnik verwendet. Durch diesen Farbraum war es möglich, Bildsignale gleichzeitig für Schwarz-Weiß- und Farbfernsehen zu kodieren.
Lineare Umrechnung zu RGB
Wie ist der LMS-Farbraum definiert? ... welche Eigenschaften hat er?

LMS ist der Zapfenfarbraum (physiologisch); Farbvalenzen beruhen auf dem Farbreiz einfallenden Lichtes. Man unterscheidet beim Menschen drei Zapfentypen, den S-Typ (Blaurezeptor), M-Typ (Grünrezeptor) und L-Typ (Rotrezeptor). Ihre Reizantwort beschreibt die spektrale Absorptionskurve, die die Grundlage der Farbmetrik bildet.
spektrale Empfindlichkeit im:
(L(ong) Rotbereich, M(iddle) Grünbereich, S(hort) Blaubereich), Zapfenfarbraum (physiologisch)
Umrechnung zu XYZ linear
Der LMS-Farbraum ist der für jeden Betrachter von Farblichtern oder gefärbten Flächen wirksame Farbraum. Er ist eine physikalisch-mathematische Darstellung des zugrunde liegenden biologisch-psychologischen Prozesses. Der LMS-Farbraum ist der eigentliche Zapfenfarbraum.
Was ist die PCA?

- Faktor 1 => Richtung der maximalen Varianz
- Datenpunkte räumlich geteilt durch Faktor 1 (rot und blau) im Bezug zum Schwerpunkt (grüner Punkt))
- Faktor 2 => Richtung der Varianz (Datenpunkte) am zweitgrößten (bzw. in diesem Fall am geringsten, da es nur 2 Achsen gibt) usw.
- Datenpunkte räumlich geteilt durch Faktor 2 (rot und blau) im Bezug zum Schwerpunkt (grüner Punkt))
Beispiel nachgerechnet mit Octave
Die PCA (Principle Component Analysis), die Hauptkomponentenanalyse verfolgt das Ziel durch Bestimmung der Hauptachsen, mit Hilfe einer kleineren Anzahl von Basisvektoren (Projektion der Daten in einen Unterraum der höherdimensionalen Messdaten) die Dimensionen der Messdaten zu reduzieren und Redundanzen zu vermeiden, ohne bzw. nur einen kleinen Teil der Informationen zu verlieren.
Sie dient dazu, umfangreiche Datensätze zu strukturieren, zu vereinfachen und zu veranschaulichen, indem eine Vielzahl statistischer Variablen durch eine geringere Zahl möglichst aussagekräftiger Linearkombinationen (die „Hauptkomponenten“) genähert wird.
Wo findet die PCA in der BV Anwendung?
Die PCA kommt aus der Statistik. In der Bildverarbeitung und speziell in der Mustererkennung wird sie verwendet um z.B. einen hochdimensionalen Feature-Raum auf die aussagekräftigsten Feature zu reduzieren. Dabei ist ein linearer Zusammenhang der einzelnen Features zu einander bedeutend. Es kann herausgefilter werden welche Features weniger zur Aussage des Musters beitragen ... oder vielleicht sogar redunant sind.
Weiter Anwendungen:
Beispiel (Schiffe charakterisieren):
Betrachtet werden Artillerieschiffe des Zweiten Weltkriegs. Sie sind eingeteilt in die Klassen Schlachtschiffe, schwere Kreuzer, leichte Kreuzer und Zerstörer. Es liegen Daten für ca. 200 Schiffe vor. Es wurden die Merkmale Länge, Breite, Wasserverdrängung, Tiefgang, Leistung der Maschinen, Geschwindigkeit (längerfristig mögliche Höchstgeschwindigkeit), Aktionsradius und Mannschaftsstärke erfasst. Eigentlich messen die Merkmale Länge, Breite, Wasserverdrängung und Tiefgang alle einen ähnlichen Sachverhalt. Man könnte hier also von einem Faktor „Größe“ sprechen. Die Frage ist, ob noch andere Faktoren die Daten bestimmen. Es gibt tatsächlich noch einen zweiten deutlichen Faktor, der vor allem durch die Leistung der Maschinen und die Höchstgeschwindigkeit bestimmt wird. Man könnte ihn zu einem Faktor „Geschwindigkeit“ zusammenfassen.
=> Ein Schiff kann im wesentlich durch nur Zwei Faktoren beschrieben werden anstatt durch die komplette Anzahl der Merkmale
=> Speicherplatz/Rechenzeit sparen / Daten anschaulicher
Das Feature "Farbe" ist z.B. als Charakterisierungsmerkmal zur Bestimmung der Leistungsfähigkeit eines Schiffes insgesamt nicht geeignet und ist als Feature unbedeutend. Es hat keinen linearen Zusammenhang im Bezug zu anderen Schiffen (Farbe kann willkürlich sein).
Weiter Anwendungen:
- Bildkompression
- Farbnormalisierung (Color-Cluster-Rotation)
- Feature-Anzahl bei Data-Mining reduzieren
- Ausdehnung eines Objektes (z.B. Binärisiert)
- Clusteranalyse
- Farbbild: Größte Ausdehnung der Punktwolke im RGB-Würfel (z.B. "Rotstich")
Beispiel (Schiffe charakterisieren):
Betrachtet werden Artillerieschiffe des Zweiten Weltkriegs. Sie sind eingeteilt in die Klassen Schlachtschiffe, schwere Kreuzer, leichte Kreuzer und Zerstörer. Es liegen Daten für ca. 200 Schiffe vor. Es wurden die Merkmale Länge, Breite, Wasserverdrängung, Tiefgang, Leistung der Maschinen, Geschwindigkeit (längerfristig mögliche Höchstgeschwindigkeit), Aktionsradius und Mannschaftsstärke erfasst. Eigentlich messen die Merkmale Länge, Breite, Wasserverdrängung und Tiefgang alle einen ähnlichen Sachverhalt. Man könnte hier also von einem Faktor „Größe“ sprechen. Die Frage ist, ob noch andere Faktoren die Daten bestimmen. Es gibt tatsächlich noch einen zweiten deutlichen Faktor, der vor allem durch die Leistung der Maschinen und die Höchstgeschwindigkeit bestimmt wird. Man könnte ihn zu einem Faktor „Geschwindigkeit“ zusammenfassen.
=> Ein Schiff kann im wesentlich durch nur Zwei Faktoren beschrieben werden anstatt durch die komplette Anzahl der Merkmale
=> Speicherplatz/Rechenzeit sparen / Daten anschaulicher
Das Feature "Farbe" ist z.B. als Charakterisierungsmerkmal zur Bestimmung der Leistungsfähigkeit eines Schiffes insgesamt nicht geeignet und ist als Feature unbedeutend. Es hat keinen linearen Zusammenhang im Bezug zu anderen Schiffen (Farbe kann willkürlich sein).
Was ist Kovarianz? Was sagt sie aus?
Die Kovarianz (cov) gibt Aussage über den linearen Zusammenhang von zwei Variablen.
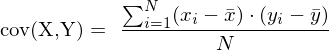
1. X,Y linear völlig unabhängig = 0
2. X,Y linear gleichsinnig abhängig = +
3. X,Y linear gegensinnig abhängig = -
=> Tendenz
Erst durch Korrelationskoeffizienten werden Daten vergleichbar => [-1..1].
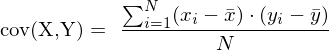
1. X,Y linear völlig unabhängig = 0
2. X,Y linear gleichsinnig abhängig = +
3. X,Y linear gegensinnig abhängig = -
=> Tendenz
Erst durch Korrelationskoeffizienten werden Daten vergleichbar => [-1..1].
Wie funktioniert die Berechnung der Hauptachsen?
1. Messdaten anordnen => Dimensionen (Variablen) in der Spalte und Messdaten (Datensätze z.B. eines Schiffes) in den Zeilen.
2. Messdaten + Matrix zentrieren (Messdaten in Ursprung des Koordinatensystems verschieben) => Mittelwert von Datenpunkten abziehen
3. Kovarianz-Matrix (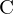 ) der Messdaten erstellen
) der Messdaten erstellen
4. Eigenwerte und Eigenvektoren von C berechnen (z.B. mit SVD)
5. Der zum größten Eigenwert korrespondierende Eigenvektor (normiert!) entspricht der eindeutigsten Hauptachse / signifikanteste Hauptachse / größter linearer Zusammenhang => analog absteigend die anderen Hauptachsen
Anmerkung: Eigenvektoren sind orthogonal zueinander
Interpretation: Drehung der Koordinatenachse in Richtung der größtmöglichen Varianz des Datensatzes.
2. Messdaten + Matrix zentrieren (Messdaten in Ursprung des Koordinatensystems verschieben) => Mittelwert von Datenpunkten abziehen
3. Kovarianz-Matrix (
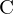 ) der Messdaten erstellen
) der Messdaten erstellen4. Eigenwerte und Eigenvektoren von C berechnen (z.B. mit SVD)
5. Der zum größten Eigenwert korrespondierende Eigenvektor (normiert!) entspricht der eindeutigsten Hauptachse / signifikanteste Hauptachse / größter linearer Zusammenhang => analog absteigend die anderen Hauptachsen
Anmerkung: Eigenvektoren sind orthogonal zueinander
Interpretation: Drehung der Koordinatenachse in Richtung der größtmöglichen Varianz des Datensatzes.
Wie verläuft die Rückrechnung der alten Daten?
1. Komponenten (Eigenvektoren und Eigenwerte) können => Komponenten mit kleiner Varianz weglassen => Hauptkomponenten auswählen
2. Projektion der Daten auf reduzierte Achsenanzahl / auf die Hauptachsen (z.B. durch Skalarprodukt) => in den Unterraum projezieren => Transformierte Messdaten
3. Inverse Matrix mit verwendeten Eigenvektoren bilden (falls alle Eigenvektoren verwendet werden geht auch Transponierte) => Matrix auf transformierte Messdaten anwenden (Rückrechnung in ursprüngliches Koordinatensystem)
4. Mittelwert wieder aufaddieren => zurück aus Zentrierung in Postion des alten Koordinatensystems
(PCA-Kompression durch weglassen von Hauptachsen ist verlustbehaftet => allerdings durch weglassen von unwichtigen Hauptachsen (kleine Eigenwerte) nur wenig Informationsverlust)
2. Projektion der Daten auf reduzierte Achsenanzahl / auf die Hauptachsen (z.B. durch Skalarprodukt) => in den Unterraum projezieren => Transformierte Messdaten
3. Inverse Matrix mit verwendeten Eigenvektoren bilden (falls alle Eigenvektoren verwendet werden geht auch Transponierte) => Matrix auf transformierte Messdaten anwenden (Rückrechnung in ursprüngliches Koordinatensystem)
4. Mittelwert wieder aufaddieren => zurück aus Zentrierung in Postion des alten Koordinatensystems
(PCA-Kompression durch weglassen von Hauptachsen ist verlustbehaftet => allerdings durch weglassen von unwichtigen Hauptachsen (kleine Eigenwerte) nur wenig Informationsverlust)
Was ist CAM? Wofür wird es verwendet?
Color Appearance Models (CAM)
Motivation: Erweiterung von physiologischen Farbräumen wie CIE L*a*b um zahlreiche weitere Einflussfaktoren der Farbwahrnehmung zu beachten
=> sollen unser Farbwahrnehmungssystem modellieren.

Motivation: Erweiterung von physiologischen Farbräumen wie CIE L*a*b um zahlreiche weitere Einflussfaktoren der Farbwahrnehmung zu beachten
=> sollen unser Farbwahrnehmungssystem modellieren.

- stellt Formeln bereit, um physikalische Messungen des Farbreizes und des Blickfeldes in die entsprechenden Farbwahrnehmungsattribute zu transformieren.
- Beispiel: Dixiklo
- Ziel: Man erreicht eine bessere Farbrepräsentation unter Abhängigkeit von mehr Eingabefaktoren
Was für Parameter gehen in ein CAM rein ... welche kommen raus?

Eingabe:
- XYZ (relativer Tristimulus)
- XwYwZw(Weißpunkt)
- relative Luminanz des Hintergrunds (
 )
) - absolute Luminanz des Blickfelds (
 )
) - Umegbungsparameter (Adaptionsfaktoren, Einfluss der Umgebung)
Ausgabe:
- brightness (Leuchtdichte/Luminanz): Objekt emittiert mehr oder weniger Licht (absolut)
- lightness (Helligkeit): Ein Objekt ist relativ hell zu einer Weißrefernz
- colorfulness (Buntheit): Absolute Farbigkeit
- chroma: Farbigkeit relativ zur Helligkeit der Weißrefernz (Farbe unter hellem Licht bunter)
- saturation: Farbigkeit relativ zur Luminanz
- hue: Farbton
Welche Effekte der menschlichen Farbwahrnehmung kennen sie?
- Simultankontrast: Hintergrundfarbe beeinflusst Wahrnehmung (grauer Kasten auf schwarzen Hintergrund => heller, grauer Kasten auf weißen Hintergrund => dunkler
- Hunt-Effekt: bei steigender Luminanz nimmt die Farbigkeit zu
- Stevens-Effekt: bei steigender Luminanz nimmt der Kontrast zu
- Surround-Effekt: Umgebung beeinflusst die Wahrnehmung
Welche Arten der Adaption kennen Sie bei der menschlichen Wahrnehmung?
Arten der Adaption
- Licht-Adaption: visuelle Sensitivität nimmt ab, wenn sich die Helligkeit erhöht
- Dunkel-Adaption: visuelle Sensitivität nimmt zu, wenn die Helligkeit sinkt
- chromatische-Adaption: Anpassung an Farbtemperatur des Umgebungslichts (Dixiklo)
Flashcard set info:
Author: JanBo
Main topic: Digitale Bildverarbeitung
Topic: IPCV
School / Univ.: Universität Koblenz-Landau
City: Koblenz
Published: 20.11.2010
Card tags:
All cards (51)
no tags






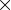 Dim Einträgen (Dim = Anzahl der Merkmale/Features/Variablen). Sie enthält alle Kovarianzen zwischen allen Dimensionen.
Dim Einträgen (Dim = Anzahl der Merkmale/Features/Variablen). Sie enthält alle Kovarianzen zwischen allen Dimensionen.