Was versteht man unter Eichen im Sinne von Relativieren? Welche Eichmaßstäbe (8) können unterschieden werden?
Unter Eichen im Sinne von Relativieren versteht man das in Bezug setzen der Testwerte, um die relative Position einer Tp bzw. ihrer Testleistung hinsichtlich der entsprechenden Referenzpopulation adäquat zu beschreiben.
Aus der Statistik - z-Wert:
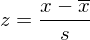
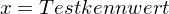
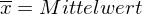
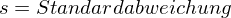
Die standardnormalverteilte Variable z als ein "Eichmaßstab" (Normwert) könnte die relative Position einer Tp bzw. ihrer Testleistung hinsichtlich der entsprechenden Referenzpopulation adäquat beschreiben.
Positive z-Werte bedeuten überdurchschnittliche, negative bedeuten unterdurchschnittliche Testleistungen. Durch die Transformation wird der Populationsmittelwert auf 0 und die Standardabweichung auf 1 gesetzt.
Von Wechsler - Wertpunkte (W)
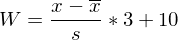
Die Transformation "mal 3" und "plus 10" ist willkürlich und entspricht dem Festlegen ("Eichen" im Sinne von Relativieren) des Maßstabs samt Null- bzw. Bezugspunkt. (Mittelwert der Population = 10 und eine Standardabweichung von 3).
Weiterer Eichmaßstab von Wechsler - IQ
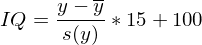
(Mittelwert von 100 und Standardabweichung von 15)
Betrachtet man die IQ-Werte und die z-Werte so sieht man folgendes: Auf einen IQ von 110 kommt man über z0=0,67; da diesem Tabellenwert p=0,25 entspricht, fallen in das Intervall 90 ≤ IQ ≤ 11ß die mittleren 50% der Referenzpopulation. Leistungen innerhalb diesen Intervalls werden üblicherweise als "durchschnittlich" bzw. "normal" beziechnet.
Weitere Eichmaßstäbe

Aus der Statistik - z-Wert:
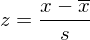
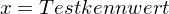
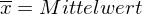
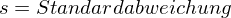
Die standardnormalverteilte Variable z als ein "Eichmaßstab" (Normwert) könnte die relative Position einer Tp bzw. ihrer Testleistung hinsichtlich der entsprechenden Referenzpopulation adäquat beschreiben.
Positive z-Werte bedeuten überdurchschnittliche, negative bedeuten unterdurchschnittliche Testleistungen. Durch die Transformation wird der Populationsmittelwert auf 0 und die Standardabweichung auf 1 gesetzt.
Von Wechsler - Wertpunkte (W)
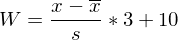
Die Transformation "mal 3" und "plus 10" ist willkürlich und entspricht dem Festlegen ("Eichen" im Sinne von Relativieren) des Maßstabs samt Null- bzw. Bezugspunkt. (Mittelwert der Population = 10 und eine Standardabweichung von 3).
Weiterer Eichmaßstab von Wechsler - IQ
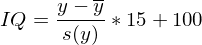
(Mittelwert von 100 und Standardabweichung von 15)
Betrachtet man die IQ-Werte und die z-Werte so sieht man folgendes: Auf einen IQ von 110 kommt man über z0=0,67; da diesem Tabellenwert p=0,25 entspricht, fallen in das Intervall 90 ≤ IQ ≤ 11ß die mittleren 50% der Referenzpopulation. Leistungen innerhalb diesen Intervalls werden üblicherweise als "durchschnittlich" bzw. "normal" beziechnet.
Weitere Eichmaßstäbe
- Z-Werte
- Centil-Werte
- Stanine-Werte ("standard-nine")
- Sten-Werte ("standard-ten")
- t-Werte
- Prozentrang
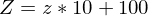
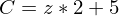
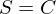 mit
mit 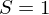 für
für 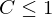 und
und 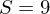 für
für 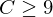
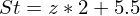
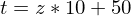

Tags: Eichmaßstäbe, Eichung
Source: S69
Source: S69
Welche z-Werte sind äußerst unwahrscheinlich? (Werte bei den anderen Eichmaßstäben)
- z-Wert: -3 ≤ z ≤ +3
- Wertpunkte W: 1 ≤ W ≤ 19
- Intelligenzquotient IQ: 55 ≤ IQ ≤ 145
- Z-Werte (Standardwerte, SW): 70 ≤ Z ≤ 130
- Centil-Werte: -1 ≤ C ≤ 11
- Sten-Werte: in 98,8% aller Fälle: 1 ≤ St ≤ 10
- T-Werte: 20 ≤ T ≤ 80

Tags: Eichmaßstäbe, Eichung
Source: S73
Source: S73
Welche Eichmaßstäbe können bei nicht-normalverteilten Testwerten verwendet werden?
Die Prozentränge sind auch bei nicht-normalverteilten Testwerten eruierbar, indem sie unmittelbar aus der Häufigkeitsfunktion der Eichstichprobe empirisch bestimmt werden.
Und die T-Werte waren ursprünglich sogar dafür gedacht, nichtnormalverteilte Testwerte in normalverteilte zu transformieren. Zum Beispiel kann für einen bestimmten Testwert, dem ein Prozentrang von 5% entspricht, leicht über die Standardnormalverteilungstabelle der zugehörigen (normalverteilte) T-Werte errechnet werden: T= (-1,645) * 10 + 50 = 33,6. Dieses Vorgehen wird als Flächentransformation bezeichnet; sie könnte natürlich auch für alle übrigen Eichmaßstäbe erfolgen.
Und die T-Werte waren ursprünglich sogar dafür gedacht, nichtnormalverteilte Testwerte in normalverteilte zu transformieren. Zum Beispiel kann für einen bestimmten Testwert, dem ein Prozentrang von 5% entspricht, leicht über die Standardnormalverteilungstabelle der zugehörigen (normalverteilte) T-Werte errechnet werden: T= (-1,645) * 10 + 50 = 33,6. Dieses Vorgehen wird als Flächentransformation bezeichnet; sie könnte natürlich auch für alle übrigen Eichmaßstäbe erfolgen.
Tags: Eichmaßstäbe, Eichung, Prozentrang
Source: S73
Source: S73
Flashcard set info:
Author: coster
Main topic: Psychologie
Topic: Psychologische Diagnostik
School / Univ.: Universität Wien
City: Wien
Published: 12.06.2013
Tags: SS2013, Holocher-Ertl
Card tags:
All cards (119)
16 PF-R (3)
AIST-R/UST-R (2)
Aufmerksamkeit (1)
Beobachten (1)
Big Five (1)
culture-fair (5)
Definition (3)
Diagnostik (15)
Eichmaßstäbe (3)
Eichung (9)
Eigenschaft (1)
Ethik (1)
Fairness (7)
Faktorenanalyse (2)
Formal (8)
Fragen (3)
Freiwillige (1)
GIS (1)
Grundsätze (6)
Gruppenverfahren (1)
Gütekriterien (1)
Intelligenz (1)
Interessen (4)
IQ (1)
Konzentration (1)
Laien (1)
Leistungsdiagnostik (13)
Memory (1)
Merkmal (1)
Messen (1)
NEO-PI-R (2)
Nützlichkeit (2)
Objektivität (5)
Ökonomie (3)
Postkorb (1)
Profil (1)
Prognose (1)
Prozentrang (2)
Prüfen (3)
Psychologe (1)
Rasch-Modell (5)
Reasoning (1)
Reliabilität (6)
Schwierigkeit (1)
Skalierung (8)
Space (1)
Test (2)
trait (1)
Validität (8)
Verfahren (3)
Voraussetzung (1)
Zumutbarkeit (2)



