Was versteht man unter einer Nullstelle?
Nenne passend zu diesem Begriff drei gleichwertige Aufgabenstellungen .
Nenne passend zu diesem Begriff drei gleichwertige Aufgabenstellungen .
Nullstellen einer Funktion sind die Zahlen, die beim Einsetzten in die Funktion den y-Wert 0 ergeben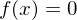 
.
Aufgabenstellung 1:
Finde die Nullstellen der Funktion f.
Aufgabenstellung 2:
Finde alle Stellen, bei denen das Schaubild der Funktion f die x-Achse schneidet oder berührt.
Aufgabenstellung 3:
Löse die Geichung f(x)=0.
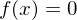.Aufgabenstellung 1:
Finde die Nullstellen der Funktion f.
Aufgabenstellung 2:
Finde alle Stellen, bei denen das Schaubild der Funktion f die x-Achse schneidet oder berührt.
Aufgabenstellung 3:
Löse die Geichung f(x)=0.
Tags: Begriffe, Nullstelle
Quelle:
Quelle:
Wie geht man bei der Nullstellensuche vor?
Welchen wichtigen Satz verwendet man hierbei?
Welchen wichtigen Satz verwendet man hierbei?
Versuche den Funktionsterm als Produkt zu schreiben.
1. Möglichst x oder x-Potenzen ausklammern.
2. Biquadratische Gleichungen durch Substitution lösen.
3. Die Summe bei Quadratische Gleichungen mit binomischen
Formeln in ein Produkt umwandeln.
4. (Polynomdivision ist nicht mehr Lehrplanstoff in Baden-Württem-
berg).
Wir überlegen bei der Nullstellensuche, für welche Zahlen die einzelnen Faktoren null ergeben. Hierbei verwenden wir den
Satz:
Ein Produkt ist genau dann null, wenn (mindestens) einer der Faktoren null ergibt.
Bemerkungen:
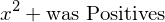kann niemals null ergeben.
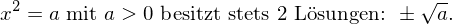
1. Möglichst x oder x-Potenzen ausklammern.
2. Biquadratische Gleichungen durch Substitution lösen.
3. Die Summe bei Quadratische Gleichungen mit binomischen
Formeln in ein Produkt umwandeln.
4. (Polynomdivision ist nicht mehr Lehrplanstoff in Baden-Württem-
berg).
Wir überlegen bei der Nullstellensuche, für welche Zahlen die einzelnen Faktoren null ergeben. Hierbei verwenden wir den
Satz:
Ein Produkt ist genau dann null, wenn (mindestens) einer der Faktoren null ergibt.
Bemerkungen:
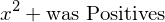kann niemals null ergeben.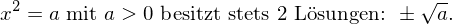Tags: Nullstelle, Produktform
Quelle:
Quelle:
Welche Eigenschaft hat die Funktion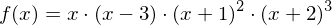 
?
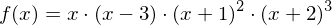?Die Funktion besitzt eine einfache Nullstelle bei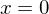 
und 
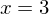, eine doppelte Nullstelle bei 
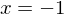und eine dreifache Nullstelle bei 
.
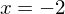Das Schaubild schneidet die x-Achse bei den einfachen Nullstellen (lokal nährungsweise wie eine Gerade), es berührt die x-Achse bei der doppelten Nullstellen (näherungsweise wie eine Parabel) und schneidet die x-Achse in einem Sattelpunkt (auch Terassenpunkt) bei der dreifachen Nullstelle (lokal wie einer Parabel dritter Ordnung).
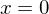und 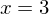, eine doppelte Nullstelle bei 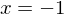und eine dreifache Nullstelle bei 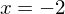.Das Schaubild schneidet die x-Achse bei den einfachen Nullstellen (lokal nährungsweise wie eine Gerade), es berührt die x-Achse bei der doppelten Nullstellen (näherungsweise wie eine Parabel) und schneidet die x-Achse in einem Sattelpunkt (auch Terassenpunkt) bei der dreifachen Nullstelle (lokal wie einer Parabel dritter Ordnung).
Tags: Funktion, Nullstelle, Produktform, Sattelpunkt, Terassenpunkt
Quelle:
Quelle:
Finde eine Funktion deren Schaubild an der Stelle 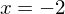und die x-Achse durchschneidet, an der Stelle 
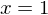die x-Achse berührt und die y-Achse im Punkt (0/6) schneidet.
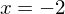und die x-Achse durchschneidet, an der Stelle 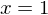die x-Achse berührt und die y-Achse im Punkt (0/6) schneidet.Für die Lösung dieser Aufgabe benötigt man nicht unbedingt die Differenzialrechnung.
Die einfache Nullstelle liefert den Faktor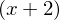
, die doppelte Nullstelle (bei x=1) entsprechend 
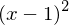. Hieraus ergibt sich eine (Hilfs-)Funktion 
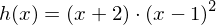, die wir so in y-Richtung strecken, dass das Schaubild der gestreckten Funktion durch (0/6) verläuft.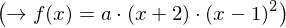 
Aus (0/6) folgt: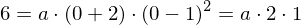
also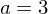
.
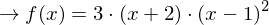
(Bei f(x) handelt es sich um eine ganzrationale Funktion, aber eine Darstellung in Summenform ist nicht gefordert! Kontrolliere das Ergebnis mit dem GTR/CAS.)
Die einfache Nullstelle liefert den Faktor
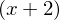, die doppelte Nullstelle (bei x=1) entsprechend 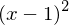. Hieraus ergibt sich eine (Hilfs-)Funktion 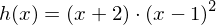, die wir so in y-Richtung strecken, dass das Schaubild der gestreckten Funktion durch (0/6) verläuft.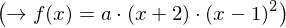 Aus (0/6) folgt:
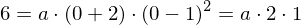
also
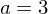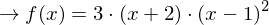
.(Bei f(x) handelt es sich um eine ganzrationale Funktion, aber eine Darstellung in Summenform ist nicht gefordert! Kontrolliere das Ergebnis mit dem GTR/CAS.)
Tags: Funktion, ganzrational, Nullstelle, Produktform, Streckung
Quelle:
Quelle:
Warum hat eine ganzrationale Funktion vom Grad n höchstens n Nullstellen?
Jede Nullstelle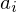 
einer ganzrationalen Funktion erzeugt in der Produktform einen Linearfaktor der Form 
.
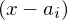Gäbe es mehr als n Nullstellen, könnte man die Funktion in der Produktdarstellung mit mehr als n Linearfaktoren darstellen. Beim Ausmultiplizieren wäre hierbei die größte x-Potenz größer als n. Das kann nicht sein.
Beachte: Es gibt natürlich ganzrationale Funktionen vom Grad n mit weniger als n Nullstellen.
Beispiel: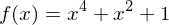
hat gar keine Nullstelle.
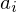einer ganzrationalen Funktion erzeugt in der Produktform einen Linearfaktor der Form 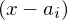. Gäbe es mehr als n Nullstellen, könnte man die Funktion in der Produktdarstellung mit mehr als n Linearfaktoren darstellen. Beim Ausmultiplizieren wäre hierbei die größte x-Potenz größer als n. Das kann nicht sein.
Beachte: Es gibt natürlich ganzrationale Funktionen vom Grad n mit weniger als n Nullstellen.
Beispiel:
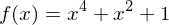hat gar keine Nullstelle.Tags: ganzrational, Grad, Nullstelle
Quelle:
Quelle:
Kartensatzinfo:
Autor: www.mathematik-bw.de
Oberthema: Mathematik
Thema: 10. Klasse
Schule / Uni: Clara-Schumann-Gymnasium
Ort: Lahr
Veröffentlicht: 23.12.2009
Schlagwörter Karten:
Alle Karten (47)
Ableitung (10)
Änderungsrate (9)
Anwendung (2)
Begriffe (17)
Definitionsmenge (1)
Extremstelle (2)
Funktion (8)
ganzrational (5)
Gerade (13)
Grad (1)
h-Methode (6)
hinreichend (3)
Intervalle (1)
Normale (2)
notwendig (2)
Nullstelle (5)
Produktform (3)
Sattelpunkt (3)
Schnittwinkel (1)
Sekante (1)
Sekantensteigung (1)
Steigungswinkel (3)
Streckung (1)
Symmetrie (3)
Tangente (7)
Terassenpunkt (3)
Verschiebung (7)
Wertemenge (1)
