Wie berechnet man den Mittelpunkt M einer Strecke 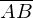 , wenn die Koordinaten von A und B gegeben sind.
, wenn die Koordinaten von A und B gegeben sind.
Wie bestimmt man den Schwerpunkt S eines Dreiecks ABC, wenn die Koordinaten der Eckpunkte gegeben sind.
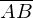 , wenn die Koordinaten von A und B gegeben sind.
, wenn die Koordinaten von A und B gegeben sind.Wie bestimmt man den Schwerpunkt S eines Dreiecks ABC, wenn die Koordinaten der Eckpunkte gegeben sind.
Die Koordinaten des Streckenmittelpunktes sind die "Durchschnitte" der jeweiligen Eckkoordinaten.
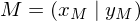 mit:
mit:
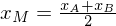 und
und 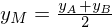 .
.
Der Schwerpunkt S eines Dreiecks errechnet sich als "physikalischer Mittelpunkt" (Besondere Punkte im Dreieck) analog:
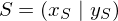 mit:
mit:
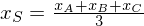 und
und 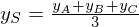 .
.
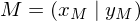 mit:
mit: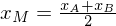 und
und 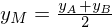 .
.Der Schwerpunkt S eines Dreiecks errechnet sich als "physikalischer Mittelpunkt" (Besondere Punkte im Dreieck) analog:
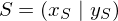 mit:
mit: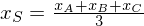 und
und 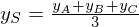 .
.Tags: Begriffe
Quelle:
Quelle:
Welcher Zusammenhang besteht zwischen dem Steigungswinkel einer Geraden und deren Steigung?
Welchen Steigungswinkel hat eine Gerade mit der Steigung 1?
Welche Werte kann ein Steigungswinkel annehmen?
Welchen Steigungswinkel hat eine Gerade mit der Steigung 1?
Welche Werte kann ein Steigungswinkel annehmen?
Mit Hilfe der Tangensbeziehung am rechtwinkligen Dreieck folgt aus dem Steigungsdreieck für den Steigungswinkel 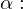
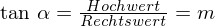 .
.
Bei einer Geraden mit der Steigung eins ist das Verhältnis aus Hochwert zu Rechtswert bei jedem Steigungsdreieck 1. Der Steigungswinkel ist hierbei Basiswinkel eines rechtwinklig gleichschenkligen Dreiecks und somit gleich 45°.
Steigungswinkel können Werte zwischen -90° und +90° annehmen. (Bei +/-90° ist die Geradensteigung nicht definiert, da die Gerade parallel zur y-Achse verläuft - der Rechtswert bei allen Steigungsdreiecken ist hier 0!)
(Lässt man keine negativen Steigungswinkel zu, liegen die Steigungswinkel zwischen 0° und 180°, wobei die Steigungen der Geraden ab 90° negativ verlaufen.)
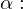
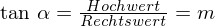 .
.Bei einer Geraden mit der Steigung eins ist das Verhältnis aus Hochwert zu Rechtswert bei jedem Steigungsdreieck 1. Der Steigungswinkel ist hierbei Basiswinkel eines rechtwinklig gleichschenkligen Dreiecks und somit gleich 45°.
Steigungswinkel können Werte zwischen -90° und +90° annehmen. (Bei +/-90° ist die Geradensteigung nicht definiert, da die Gerade parallel zur y-Achse verläuft - der Rechtswert bei allen Steigungsdreiecken ist hier 0!)
(Lässt man keine negativen Steigungswinkel zu, liegen die Steigungswinkel zwischen 0° und 180°, wobei die Steigungen der Geraden ab 90° negativ verlaufen.)
Tags: Begriffe, Gerade, Steigungswinkel
Quelle:
Quelle:
Woran erkennt man bereits an den Punktkoordinaten zweier Geradenpunkte, ob der Steigungswinkel der Geraden negativ ist?
Liegt der y-Wert des rechten Punktes unterhalb des y-Wertes des linken, dann "fällt die Gerade an". Der Steigungswinkel (und die Steigung) ist in diesen Fällen negativ.
Tags: Begriffe, Gerade, Steigungswinkel
Quelle:
Quelle:
Wie bestimmt man den Schnittwinkel zwischen zwei Geraden?
Erstelle zunächst eine Skizze!
Bestimme die Steigungswinkel zu jeder einzelnen Geraden und errechne hieraus den Wert für die Steigungswinkel beider Geraden.
Beachte, dass man je nach Lage der Geraden die Steigungswinkel addieren bzw. voneinander subtrahieren muss. Aus diesem Grund ist bei dieser Aufgabenstellung eine Skizze unbedingt zu empfehlen.
Linktipp: Landesbildungsserver Baden-Württemberg
Bestimme die Steigungswinkel zu jeder einzelnen Geraden und errechne hieraus den Wert für die Steigungswinkel beider Geraden.
Beachte, dass man je nach Lage der Geraden die Steigungswinkel addieren bzw. voneinander subtrahieren muss. Aus diesem Grund ist bei dieser Aufgabenstellung eine Skizze unbedingt zu empfehlen.
Linktipp: Landesbildungsserver Baden-Württemberg
Tags: Begriffe, Gerade, Schnittwinkel, Steigungswinkel
Quelle:
Quelle:
Skizziere die Schaubilder der Kehrwertfunktion, der Quadratfunktion und der Wurzelfunktion.
Wie nennt man das Schaubild der Kehrwertfunktion?
Was ist eine „Antiproportionalität“?
Wie nennt man das Schaubild der Kehrwertfunktion?
Was ist eine „Antiproportionalität“?
Antwort 
Schaubild der Kehrwertfunktion heißt Hyperbel: blau
Schaubild der Quadratfunktion (heißt Nomalparabel): rot
Schaubild der Wurzelfunktion: grün
Eine Antiproportionalität ist eine „gestreckte“ Kehrwertfunktion. Das Verdoppeln des x-Wertes bewirkt stets eine Halbierung des entsprechenden Funktionswertes.
Linktipp: Die wichtigsten Funktionen mit ihren Schaubildern

Schaubild der Kehrwertfunktion heißt Hyperbel: blau
Schaubild der Quadratfunktion (heißt Nomalparabel): rot
Schaubild der Wurzelfunktion: grün
Eine Antiproportionalität ist eine „gestreckte“ Kehrwertfunktion. Das Verdoppeln des x-Wertes bewirkt stets eine Halbierung des entsprechenden Funktionswertes.
Linktipp: Die wichtigsten Funktionen mit ihren Schaubildern
Tags: Begriffe, Funktion
Quelle:
Quelle:
Wie bestimmt man die momentane/lokale Änderungsrate einer Funktion f an einer Stelle x (mit der h-Methode)?
Man wählt zu einer Stelle  eine „Nachbarstelle“
eine „Nachbarstelle“ 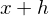 und bildet mit den zugehörigen Funktionswerten
und bildet mit den zugehörigen Funktionswerten 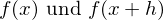 den so genannten Differenzenquotienten
den so genannten Differenzenquotienten 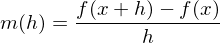
Durch Ausklammern von h im Zähler und durch Kürzen mit h (bzw. geschicktes Umformen) wird der Bruch „reif für den Grenzübergang“: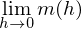 .
.
Nur wenn die Funktionsvariable (x) eine Zeit beschreibt, spricht man von momentaner Änderungsrate. In allen anderen Fällen sagt man lokale Änderungsrate.
Geometrisch entspricht dieser Grenzübergang dem Übergang von einer Sekante zur Tangenten.
Linktipp: Von der Sekanten zur Tangenten
 eine „Nachbarstelle“
eine „Nachbarstelle“ 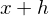 und bildet mit den zugehörigen Funktionswerten
und bildet mit den zugehörigen Funktionswerten 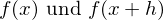 den so genannten Differenzenquotienten
den so genannten Differenzenquotienten 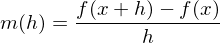
Durch Ausklammern von h im Zähler und durch Kürzen mit h (bzw. geschicktes Umformen) wird der Bruch „reif für den Grenzübergang“:
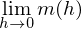 .
.Nur wenn die Funktionsvariable (x) eine Zeit beschreibt, spricht man von momentaner Änderungsrate. In allen anderen Fällen sagt man lokale Änderungsrate.
Geometrisch entspricht dieser Grenzübergang dem Übergang von einer Sekante zur Tangenten.
Linktipp: Von der Sekanten zur Tangenten
Tags: Ableitung, Ableitungsfunktion, Änderungsrate, Begriffe, Differenzenquotient, h-Methode
Quelle:
Quelle:
Bestimme die Änderungsrate der Kreisfläche an der Stelle r=4 cm. Handelt es sich um eine lokale oder momentane ÄndR?
Wie groß ist die Änderungsrate an der Stelle r=10 cm?
Wie groß ist die Änderungsrate an der Stelle r=10 cm?
Da die Kreisfläche nicht von der Zeit abhängt, handelt es sich um eine lokale ÄndR.
Bestandsfunktion: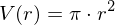
Differenzenquotient: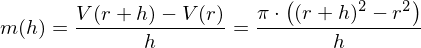
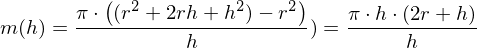
Der Differenzenquotient ist nun "reif für den Grenzübergang", denn nach dem Kürzen mit h kann der Nenner nicht mehr null werden.
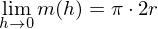
Hieraus folgt für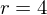 die lokale ÄndR
die lokale ÄndR 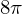 und für
und für 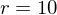 die lokale ÄndR
die lokale ÄndR 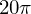 .
.
Bestandsfunktion:
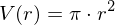
Differenzenquotient:
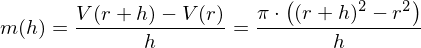
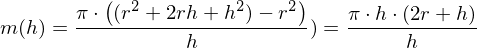
Der Differenzenquotient ist nun "reif für den Grenzübergang", denn nach dem Kürzen mit h kann der Nenner nicht mehr null werden.
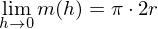
Hieraus folgt für
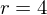 die lokale ÄndR
die lokale ÄndR 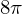 und für
und für 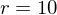 die lokale ÄndR
die lokale ÄndR 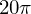 .
.Tags: Ableitung, Ableitungsfunktion, Änderungsrate, Begriffe, Differenzenquotient, h-Methode
Quelle:
Quelle:
Wie ist die Ableitung einer Funktion an einer Stelle x definiert?
Die Ableitung einer Funktion f an einer Stelle x ist über den Grenzwert des Differenzenquotienten definiert:
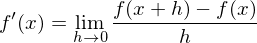
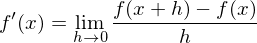
Tags: Ableitung, Ableitungsfunktion, Begriffe, Differenzenquotient, h-Methode
Quelle:
Quelle:
Zeige mit der Definition der Ableitung, dass die Ableitungsfunktion von 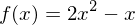 gleich
gleich 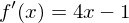 ist.
ist.
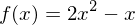 gleich
gleich 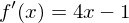 ist.
ist.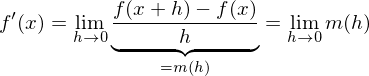
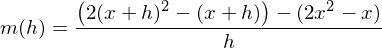
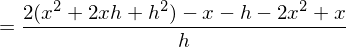
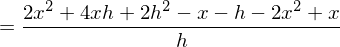
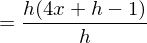
Kürzen mit h und Durchführung des Grenzübergangs führt zum Ergebnis:
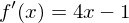
Achtung: Häufige Rechenfehler beim Aufstellen des Differenzenquotienten, da Minusklammern auftreten, sobald die Funktion aus einer Summe oder Differenz besteht.
Tags: Ableitung, Ableitungsfunktion, Begriffe, h-Methode
Quelle:
Quelle:
Zeige mit der Definition der Ableitung, dass die Ableitungsfunktion von 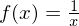 gleich
gleich 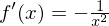 ist.
ist.
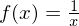 gleich
gleich 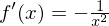 ist.
ist.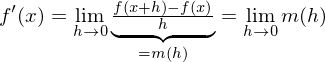
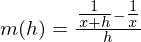 (HN im Zähler ist
(HN im Zähler ist 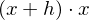 )
)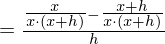
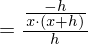
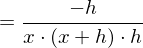
Kürzen mit h und Durchführung des Grenzübergangs führt zum Ergebnis:
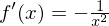
Achtung: Beachte, dass das Minuszeichen in der dritten Zeile auf
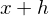 wirkt. Hierdurch kommt das Minus im Ergebnis zustande.
wirkt. Hierdurch kommt das Minus im Ergebnis zustande.Tags: Ableitung, Ableitungsfunktion, Begriffe, h-Methode
Quelle:
Quelle:
Zeige mit der Definition der Ableitung, dass die Ableitungsfunktion von 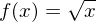 gleich
gleich 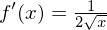 ist.
ist.
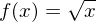 gleich
gleich 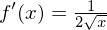 ist.
ist.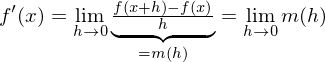
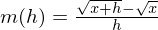 (Wurzel im Zähler verschwinden durch "geschicktes" Erweitern)
(Wurzel im Zähler verschwinden durch "geschicktes" Erweitern)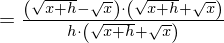
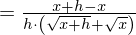
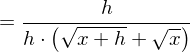
Kürzen mit h und Durchführung des Grenzübergangs führt zum Ergebnis:
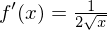
Achtung: Beim "geschickten" Erweitern wurde die dritte binomische Formel ausgenutzt.
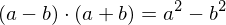
und
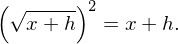
Tags: Ableitung, Ableitungsfunktion, Begriffe, h-Methode
Quelle:
Quelle:
Bei einer Funktion f gilt für alle 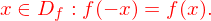
Was bedeutet dies für das zugehörige Schaubild?
Nenne drei unterschiedliche Funktionstypen mit dieser Eigenschaft in der allgemeinen Form.
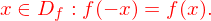
Was bedeutet dies für das zugehörige Schaubild?
Nenne drei unterschiedliche Funktionstypen mit dieser Eigenschaft in der allgemeinen Form.
Aus der Bedingung folgt die (Achsen-)Symmetrie des Schaubildes von f zur y-Achse
Beachte, dass man die entsprechende Funktion als "gerade" bezeichnet - nicht aber das Schaubild!
Beispiele:
- Jede konstante Funktion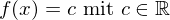
- Potenzfunktionen mit gerader, ganzzahligen Hochzahl:
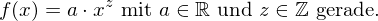
- Jede ganzrationale Funktion mit ausschließlich geraden
"x-Potenzen" .
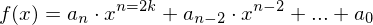
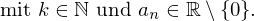
- Die Kosinusfunktion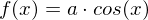 mit beliebigem
mit beliebigem
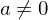 .
.
- Die Nullfunktion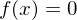 . (Einzige Funktion die sowohl
. (Einzige Funktion die sowohl
gerade, als auch ungerade ist.)
Bemerkungen:
In Worten bedeutet die obige Gleichung: "Betrachtet man
auf der x-Achse eine Zahl und ihre Gegenzahl, so sind auch die entsprechenden y-Werte identisch."
Gerade Zahlen haben immer die Form eines Produkt aus einer natürlichen Zahl mit 2.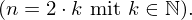
Beachte, dass man die entsprechende Funktion als "gerade" bezeichnet - nicht aber das Schaubild!
Beispiele:
- Jede konstante Funktion
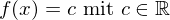
- Potenzfunktionen mit gerader, ganzzahligen Hochzahl:
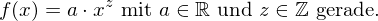
- Jede ganzrationale Funktion mit ausschließlich geraden
"x-Potenzen" .
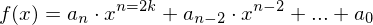
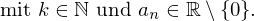
- Die Kosinusfunktion
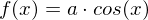 mit beliebigem
mit beliebigem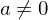 .
.- Die Nullfunktion
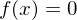 . (Einzige Funktion die sowohl
. (Einzige Funktion die sowohlgerade, als auch ungerade ist.)
Bemerkungen:
In Worten bedeutet die obige Gleichung: "Betrachtet man
auf der x-Achse eine Zahl und ihre Gegenzahl, so sind auch die entsprechenden y-Werte identisch."
Gerade Zahlen haben immer die Form eines Produkt aus einer natürlichen Zahl mit 2.
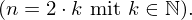
Tags: Begriffe, Funktion, ganzrational, Symmetrie
Quelle:
Quelle:
Bei einer Funktion f gilt für alle 
Was bedeutet dies für das zugehörige Schaubild?
Nenne drei unterschiedliche Funktionstypen mit dieser Eigenschaft in der allgemeinen Form.

Was bedeutet dies für das zugehörige Schaubild?
Nenne drei unterschiedliche Funktionstypen mit dieser Eigenschaft in der allgemeinen Form.
Aus der Bedingung folgt die Punktsymmetrie des Schaubildes von f zum Ursprung
Beachte, dass man die entsprechende Funktion als "ungerade" bezeichnet - nicht aber das Schaubild!
Beispiele:
- Jede Proportionalität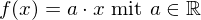 oder
oder
allg. Potenzfktn. mit ungerader, ganzzahliger Hochzahl
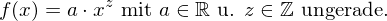 .
.
Hierzu zählt auch die Kehrwertfunktion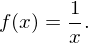
- Jede ganzrationale Funktion mit ausschließlich ungeraden
"x-Potenzen"
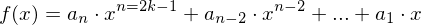
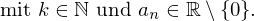
- Die Sinusfunktion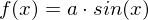 mit beliebigem
mit beliebigem
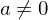 .
.
- Die Nullfunktion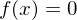 . (Einzige Funktion die sowohl
. (Einzige Funktion die sowohl
gerade, als auch ungerade ist.)
Bemerkungen:
In Worten bedeutet die obige Gleichung: "Betrachtet man
auf der x-Achse eine Zahl und ihre Gegenzahl, so sind auch die entsprechenden y-Werte jeweils Zahl und Gegenzahl."
Ungerade Zahlen haben immer die Form eines Produkt aus einer natürlichen Zahl mit 2 abzüglich oder zuzüglich 1.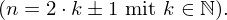
Beachte, dass man die entsprechende Funktion als "ungerade" bezeichnet - nicht aber das Schaubild!
Beispiele:
- Jede Proportionalität
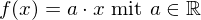 oder
oder allg. Potenzfktn. mit ungerader, ganzzahliger Hochzahl
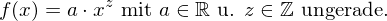 .
. Hierzu zählt auch die Kehrwertfunktion
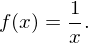
- Jede ganzrationale Funktion mit ausschließlich ungeraden
"x-Potenzen"
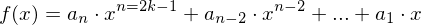
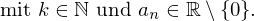
- Die Sinusfunktion
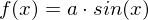 mit beliebigem
mit beliebigem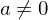 .
.- Die Nullfunktion
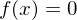 . (Einzige Funktion die sowohl
. (Einzige Funktion die sowohlgerade, als auch ungerade ist.)
Bemerkungen:
In Worten bedeutet die obige Gleichung: "Betrachtet man
auf der x-Achse eine Zahl und ihre Gegenzahl, so sind auch die entsprechenden y-Werte jeweils Zahl und Gegenzahl."
Ungerade Zahlen haben immer die Form eines Produkt aus einer natürlichen Zahl mit 2 abzüglich oder zuzüglich 1.
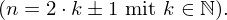
Tags: Begriffe, Funktion, ganzrational, Symmetrie
Quelle:
Quelle:
Was versteht man unter einer Nullstelle?
Nenne passend zu diesem Begriff drei gleichwertige Aufgabenstellungen .
Nenne passend zu diesem Begriff drei gleichwertige Aufgabenstellungen .
Nullstellen einer Funktion sind die Zahlen, die beim Einsetzten in die Funktion den y-Wert 0 ergeben 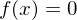 .
.
Aufgabenstellung 1:
Finde die Nullstellen der Funktion f.
Aufgabenstellung 2:
Finde alle Stellen, bei denen das Schaubild der Funktion f die x-Achse schneidet oder berührt.
Aufgabenstellung 3:
Löse die Geichung f(x)=0.
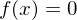 .
.Aufgabenstellung 1:
Finde die Nullstellen der Funktion f.
Aufgabenstellung 2:
Finde alle Stellen, bei denen das Schaubild der Funktion f die x-Achse schneidet oder berührt.
Aufgabenstellung 3:
Löse die Geichung f(x)=0.
Tags: Begriffe, Nullstelle
Quelle:
Quelle:
Was versteht man unter den charakteristischen Punkten eines Schaubildes?
Hochpunkte, Tiefpunkte und die Schnittpunkte mit den Koordinatenachsen.
Tags: Begriffe
Quelle:
Quelle:
Erkläre das hinreichende Kriterium für Extremstellen mit dem VZ-Wechsel der ersten Ableitung.
Wenn die Ableitungsfunktion f' negative Werte besitzt, bedeutet das für die Stammfunktion f, dass die y-Werte abnehmen (zugehöriges Schaubild fällt) - bei positiven Werten von f' nehmen die y-Werte von f zu (Schaubild von f steigt).
Damit bedeutet ein VZ-Wechsel bei f' von Minus nach Plus, dass hier bei f ein ein Übergang von abnehmenden nach zunehmenden y-Werten stattfindet - dies überführt eine Minimalstelle.
Bei einer Maximalstelle ist es umgekehrt.
Betrachte hierzu auch das YouTube-Video Hinreichende Bedingung für Extremstelle
Damit bedeutet ein VZ-Wechsel bei f' von Minus nach Plus, dass hier bei f ein ein Übergang von abnehmenden nach zunehmenden y-Werten stattfindet - dies überführt eine Minimalstelle.
Bei einer Maximalstelle ist es umgekehrt.
Betrachte hierzu auch das YouTube-Video Hinreichende Bedingung für Extremstelle
Tags: Begriffe, Extremstelle, hinreichend
Quelle:
Quelle:
Welche notwendigen und hinreichenden Bedingungen muss eine (differenzierbare) Funktion erfüllen, wenn beim zugehörigen Schaubild an einer Stelle  ein Sattelpunkt (oder Terassenpunkt) vorliegt?
ein Sattelpunkt (oder Terassenpunkt) vorliegt?
 ein Sattelpunkt (oder Terassenpunkt) vorliegt?
ein Sattelpunkt (oder Terassenpunkt) vorliegt?Bei einem Sattelpunkt (auch Terassenpunkt) muss an der entsprechenden Stelle  die Ableitungsfunktion f' den Wert null besitzten (Sattelpunkte haben waagerechte Tangenten), rechts und links von
die Ableitungsfunktion f' den Wert null besitzten (Sattelpunkte haben waagerechte Tangenten), rechts und links von  muss f' entweder nur positive Werte oder nur negative Werte besitzten.
muss f' entweder nur positive Werte oder nur negative Werte besitzten.
Jede dieser zwei Bedingungen ist notwendig für einen Sattelpunkt - nur wenn beide Bedingungen gleichzeitig erfüllt sind, können wir an dieser Stelle sicher auf einen Sattelpunkt schließen - sie sind hierfür hinreichend.
Ebenfalls hinreichend für einen Sattelpunkt an der Stelle ist die Bedingung, dass sowohl
ist die Bedingung, dass sowohl 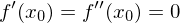 als auch
als auch 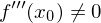 gilt.
gilt.
 die Ableitungsfunktion f' den Wert null besitzten (Sattelpunkte haben waagerechte Tangenten), rechts und links von
die Ableitungsfunktion f' den Wert null besitzten (Sattelpunkte haben waagerechte Tangenten), rechts und links von  muss f' entweder nur positive Werte oder nur negative Werte besitzten.
muss f' entweder nur positive Werte oder nur negative Werte besitzten. Jede dieser zwei Bedingungen ist notwendig für einen Sattelpunkt - nur wenn beide Bedingungen gleichzeitig erfüllt sind, können wir an dieser Stelle sicher auf einen Sattelpunkt schließen - sie sind hierfür hinreichend.
Ebenfalls hinreichend für einen Sattelpunkt an der Stelle
 ist die Bedingung, dass sowohl
ist die Bedingung, dass sowohl 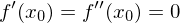 als auch
als auch 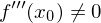 gilt.
gilt.Tags: Begriffe, Funktion, hinreichend, notwendig, Sattelpunkt, Terassenpunkt
Quelle:
Quelle:
Kartensatzinfo:
Autor: www.mathematik-bw.de
Oberthema: Mathematik
Thema: 10. Klasse
Schule / Uni: Clara-Schumann-Gymnasium
Ort: Lahr
Veröffentlicht: 23.12.2009
Schlagwörter Karten:
Alle Karten (47)
Ableitung (10)
Änderungsrate (9)
Anwendung (2)
Begriffe (17)
Definitionsmenge (1)
Extremstelle (2)
Funktion (8)
ganzrational (5)
Gerade (13)
Grad (1)
h-Methode (6)
hinreichend (3)
Intervalle (1)
Normale (2)
notwendig (2)
Nullstelle (5)
Produktform (3)
Sattelpunkt (3)
Schnittwinkel (1)
Sekante (1)
Sekantensteigung (1)
Steigungswinkel (3)
Streckung (1)
Symmetrie (3)
Tangente (7)
Terassenpunkt (3)
Verschiebung (7)
Wertemenge (1)



