Wie bestimmt man die momentane/lokale Änderungsrate einer Funktion f an einer Stelle x (mit der h-Methode)?
Man wählt zu einer Stelle  eine „Nachbarstelle“
eine „Nachbarstelle“ 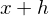 und bildet mit den zugehörigen Funktionswerten
und bildet mit den zugehörigen Funktionswerten 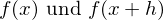 den so genannten Differenzenquotienten
den so genannten Differenzenquotienten 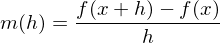
Durch Ausklammern von h im Zähler und durch Kürzen mit h (bzw. geschicktes Umformen) wird der Bruch „reif für den Grenzübergang“: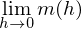 .
.
Nur wenn die Funktionsvariable (x) eine Zeit beschreibt, spricht man von momentaner Änderungsrate. In allen anderen Fällen sagt man lokale Änderungsrate.
Geometrisch entspricht dieser Grenzübergang dem Übergang von einer Sekante zur Tangenten.
Linktipp: Von der Sekanten zur Tangenten
 eine „Nachbarstelle“
eine „Nachbarstelle“ 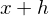 und bildet mit den zugehörigen Funktionswerten
und bildet mit den zugehörigen Funktionswerten 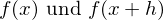 den so genannten Differenzenquotienten
den so genannten Differenzenquotienten 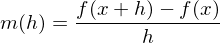
Durch Ausklammern von h im Zähler und durch Kürzen mit h (bzw. geschicktes Umformen) wird der Bruch „reif für den Grenzübergang“:
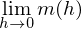 .
.Nur wenn die Funktionsvariable (x) eine Zeit beschreibt, spricht man von momentaner Änderungsrate. In allen anderen Fällen sagt man lokale Änderungsrate.
Geometrisch entspricht dieser Grenzübergang dem Übergang von einer Sekante zur Tangenten.
Linktipp: Von der Sekanten zur Tangenten
Tags: Ableitung, Ableitungsfunktion, Änderungsrate, Begriffe, Differenzenquotient, h-Methode
Quelle:
Quelle:
Bestimme die Änderungsrate der Kreisfläche an der Stelle r=4 cm. Handelt es sich um eine lokale oder momentane ÄndR?
Wie groß ist die Änderungsrate an der Stelle r=10 cm?
Wie groß ist die Änderungsrate an der Stelle r=10 cm?
Da die Kreisfläche nicht von der Zeit abhängt, handelt es sich um eine lokale ÄndR.
Bestandsfunktion: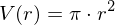
Differenzenquotient: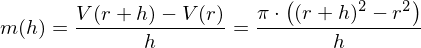
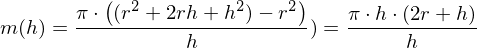
Der Differenzenquotient ist nun "reif für den Grenzübergang", denn nach dem Kürzen mit h kann der Nenner nicht mehr null werden.
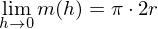
Hieraus folgt für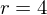 die lokale ÄndR
die lokale ÄndR 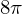 und für
und für 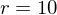 die lokale ÄndR
die lokale ÄndR 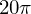 .
.
Bestandsfunktion:
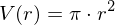
Differenzenquotient:
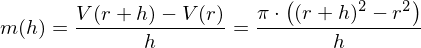
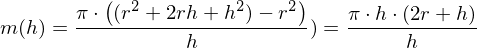
Der Differenzenquotient ist nun "reif für den Grenzübergang", denn nach dem Kürzen mit h kann der Nenner nicht mehr null werden.
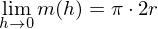
Hieraus folgt für
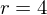 die lokale ÄndR
die lokale ÄndR 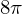 und für
und für 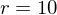 die lokale ÄndR
die lokale ÄndR 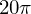 .
.Tags: Ableitung, Ableitungsfunktion, Änderungsrate, Begriffe, Differenzenquotient, h-Methode
Quelle:
Quelle:
Wie ist die Ableitung einer Funktion an einer Stelle x definiert?
Die Ableitung einer Funktion f an einer Stelle x ist über den Grenzwert des Differenzenquotienten definiert:
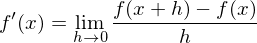
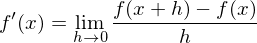
Tags: Ableitung, Ableitungsfunktion, Begriffe, Differenzenquotient, h-Methode
Quelle:
Quelle:
Zeige mit der Definition der Ableitung, dass die Ableitungsfunktion von 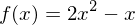 gleich
gleich 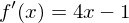 ist.
ist.
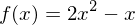 gleich
gleich 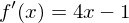 ist.
ist.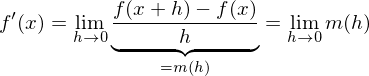
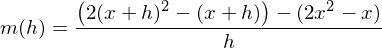
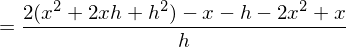
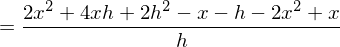
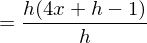
Kürzen mit h und Durchführung des Grenzübergangs führt zum Ergebnis:
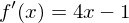
Achtung: Häufige Rechenfehler beim Aufstellen des Differenzenquotienten, da Minusklammern auftreten, sobald die Funktion aus einer Summe oder Differenz besteht.
Tags: Ableitung, Ableitungsfunktion, Begriffe, h-Methode
Quelle:
Quelle:
Zeige mit der Definition der Ableitung, dass die Ableitungsfunktion von 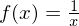 gleich
gleich 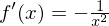 ist.
ist.
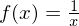 gleich
gleich 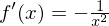 ist.
ist.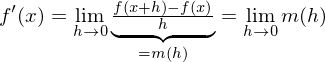
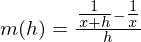 (HN im Zähler ist
(HN im Zähler ist 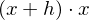 )
)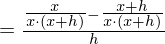
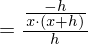
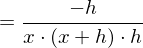
Kürzen mit h und Durchführung des Grenzübergangs führt zum Ergebnis:
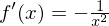
Achtung: Beachte, dass das Minuszeichen in der dritten Zeile auf
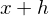 wirkt. Hierdurch kommt das Minus im Ergebnis zustande.
wirkt. Hierdurch kommt das Minus im Ergebnis zustande.Tags: Ableitung, Ableitungsfunktion, Begriffe, h-Methode
Quelle:
Quelle:
Zeige mit der Definition der Ableitung, dass die Ableitungsfunktion von 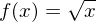 gleich
gleich 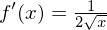 ist.
ist.
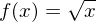 gleich
gleich 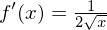 ist.
ist.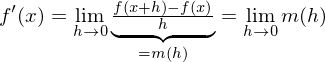
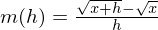 (Wurzel im Zähler verschwinden durch "geschicktes" Erweitern)
(Wurzel im Zähler verschwinden durch "geschicktes" Erweitern)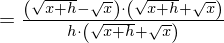
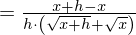
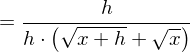
Kürzen mit h und Durchführung des Grenzübergangs führt zum Ergebnis:
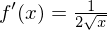
Achtung: Beim "geschickten" Erweitern wurde die dritte binomische Formel ausgenutzt.
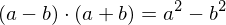
und
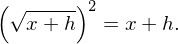
Tags: Ableitung, Ableitungsfunktion, Begriffe, h-Methode
Quelle:
Quelle:
Was lässt sich über das Schaubild einer Funktion f sagen, wenn das Schaubild der zugehörigen Ableitungsfunktion f' an einer Stelle x die x-Achse von unten nach oben durchschneidet?
Die Steigungen des Schaubildes von f sind links von x negativ und rechts von x positiv. Damit liegt an der Stelle x eine Maximalstelle vor.
Animation: Informationen aus dem Schaubild von f'(x).
Animation: Informationen aus dem Schaubild von f'(x).
Tags: Ableitung, Ableitungsfunktion
Quelle:
Quelle:
Was lässt sich über das Schaubild einer Funktion f sagen, wenn das Schaubild der zugehörigen Ableitungsfunktion f' an einer Stelle x die x-Achse berührt, aber nicht durchschneidet?
Links und rechts von der Stelle x sind die Steigungen des Schaubildes von f jeweils positiv,falls das Schaubild von f' die x-Achse von oben berührt andernfalls negativ.
An der Stelle x ist die Steigung des Schaubildes von f null. Somit liegt an dieser Stelle ein Sattelpunkt des Schaubildes von f.
Setzte den ersten und den dritten Haken bei Animation: Informationen aus dem Schaubild von f'(x) und stelle anschließend den roten Schieberegler (y Verschiebung) auf null.
An der Stelle x ist die Steigung des Schaubildes von f null. Somit liegt an dieser Stelle ein Sattelpunkt des Schaubildes von f.
Setzte den ersten und den dritten Haken bei Animation: Informationen aus dem Schaubild von f'(x) und stelle anschließend den roten Schieberegler (y Verschiebung) auf null.
Tags: Ableitung, Ableitungsfunktion
Quelle:
Quelle:
Wie lässt sich die Existenz eines Hochpunktes aus dem Schaubild der Ableitungsfunktion ablesen?
Links von einem Hochpunkt findet man stets positive Tangentensteigungen, rechts davon sind sie negativ. Damit liegt an jeder Stelle, an der das Schaubild der Ableitungsfunktion f'(x) die x-Achse von oben nach unten durchschneidet ein Hochpunkt im Schaubild von f(x).
Animation: Informationen aus dem Schaubild von f'(x).
Animation: Informationen aus dem Schaubild von f'(x).
Tags: Ableitung, Ableitungsfunktion
Quelle:
Quelle:
Kartensatzinfo:
Autor: www.mathematik-bw.de
Oberthema: Mathematik
Thema: 10. Klasse
Schule / Uni: Clara-Schumann-Gymnasium
Ort: Lahr
Veröffentlicht: 23.12.2009
Schlagwörter Karten:
Alle Karten (47)
Ableitung (10)
Ableitungsfunktion (9)
Änderungsrate (9)
Anwendung (2)
Begriffe (17)
Definitionsmenge (1)
Extremstelle (2)
Funktion (8)
ganzrational (5)
Gerade (13)
Grad (1)
h-Methode (6)
hinreichend (3)
Intervalle (1)
Normale (2)
notwendig (2)
Nullstelle (5)
Produktform (3)
Sattelpunkt (3)
Schnittwinkel (1)
Sekante (1)
Sekantensteigung (1)
Steigungswinkel (3)
Streckung (1)
Symmetrie (3)
Tangente (7)
Terassenpunkt (3)
Verschiebung (7)
Wertemenge (1)



