Wie löst man das folgende Tangentenproblem (Typ 2):
Eine Tangentensteigung ist gegeben. Gesucht ist/sind die Tangente(n) an das Schaubild mit dieser Steigung.
Eine Tangentensteigung ist gegeben. Gesucht ist/sind die Tangente(n) an das Schaubild mit dieser Steigung.
Leite die Funktion zum Schaubild ab und setzte die Ableitungsfunktion mit der gegebenen Steigung gleich. Die Gleichung besitzt eine oder mehrere Lösungen, je nachdem, ob es eine oder mehrere Tangenten mit der geforderten Steigung gibt.
Jede Lösung entspricht dem x-Wert eines Berührpunktes. Den zugehörigen y-Wert erhält man durch Einsetzen des x-Wertes in f(x).
Durch Verschiebung der Ursprungsgeraden mit der geforderten Steigung in x- und y-Richtung erhalten wir die Tangentengleichung:
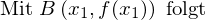
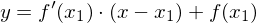
Bemerkungen:
Beim Schaubild der Kehrwertfunktion gibt es für alle Steigungen außer m=0 zwei Tangenten.
Bei Parabeln gerader Ordnung gibt es zu jeder Steigung genau eine Lösung.
Bei ganzrationalen Funktionen mit einem Grad > 2 kann es mehrere Lösungen geben.
Jede Lösung entspricht dem x-Wert eines Berührpunktes. Den zugehörigen y-Wert erhält man durch Einsetzen des x-Wertes in f(x).
Durch Verschiebung der Ursprungsgeraden mit der geforderten Steigung in x- und y-Richtung erhalten wir die Tangentengleichung:
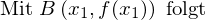
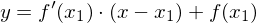
Bemerkungen:
Beim Schaubild der Kehrwertfunktion gibt es für alle Steigungen außer m=0 zwei Tangenten.
Bei Parabeln gerader Ordnung gibt es zu jeder Steigung genau eine Lösung.
Bei ganzrationalen Funktionen mit einem Grad > 2 kann es mehrere Lösungen geben.
Tags: ganzrational, Tangente, Verschiebung
Source:
Source:
Bei einer Funktion f gilt für alle 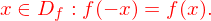
Was bedeutet dies für das zugehörige Schaubild?
Nenne drei unterschiedliche Funktionstypen mit dieser Eigenschaft in der allgemeinen Form.
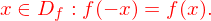
Was bedeutet dies für das zugehörige Schaubild?
Nenne drei unterschiedliche Funktionstypen mit dieser Eigenschaft in der allgemeinen Form.
Aus der Bedingung folgt die (Achsen-)Symmetrie des Schaubildes von f zur y-Achse
Beachte, dass man die entsprechende Funktion als "gerade" bezeichnet - nicht aber das Schaubild!
Beispiele:
- Jede konstante Funktion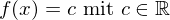
- Potenzfunktionen mit gerader, ganzzahligen Hochzahl:
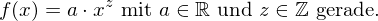
- Jede ganzrationale Funktion mit ausschließlich geraden
"x-Potenzen" .
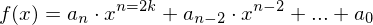
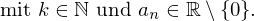
- Die Kosinusfunktion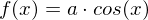 mit beliebigem
mit beliebigem
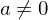 .
.
- Die Nullfunktion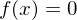 . (Einzige Funktion die sowohl
. (Einzige Funktion die sowohl
gerade, als auch ungerade ist.)
Bemerkungen:
In Worten bedeutet die obige Gleichung: "Betrachtet man
auf der x-Achse eine Zahl und ihre Gegenzahl, so sind auch die entsprechenden y-Werte identisch."
Gerade Zahlen haben immer die Form eines Produkt aus einer natürlichen Zahl mit 2.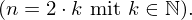
Beachte, dass man die entsprechende Funktion als "gerade" bezeichnet - nicht aber das Schaubild!
Beispiele:
- Jede konstante Funktion
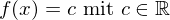
- Potenzfunktionen mit gerader, ganzzahligen Hochzahl:
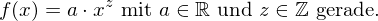
- Jede ganzrationale Funktion mit ausschließlich geraden
"x-Potenzen" .
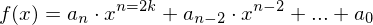
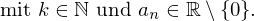
- Die Kosinusfunktion
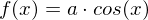 mit beliebigem
mit beliebigem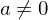 .
.- Die Nullfunktion
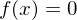 . (Einzige Funktion die sowohl
. (Einzige Funktion die sowohlgerade, als auch ungerade ist.)
Bemerkungen:
In Worten bedeutet die obige Gleichung: "Betrachtet man
auf der x-Achse eine Zahl und ihre Gegenzahl, so sind auch die entsprechenden y-Werte identisch."
Gerade Zahlen haben immer die Form eines Produkt aus einer natürlichen Zahl mit 2.
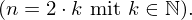
Tags: Begriffe, Funktion, ganzrational, Symmetrie
Source:
Source:
Bei einer Funktion f gilt für alle 
Was bedeutet dies für das zugehörige Schaubild?
Nenne drei unterschiedliche Funktionstypen mit dieser Eigenschaft in der allgemeinen Form.

Was bedeutet dies für das zugehörige Schaubild?
Nenne drei unterschiedliche Funktionstypen mit dieser Eigenschaft in der allgemeinen Form.
Aus der Bedingung folgt die Punktsymmetrie des Schaubildes von f zum Ursprung
Beachte, dass man die entsprechende Funktion als "ungerade" bezeichnet - nicht aber das Schaubild!
Beispiele:
- Jede Proportionalität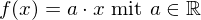 oder
oder
allg. Potenzfktn. mit ungerader, ganzzahliger Hochzahl
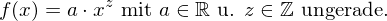 .
.
Hierzu zählt auch die Kehrwertfunktion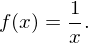
- Jede ganzrationale Funktion mit ausschließlich ungeraden
"x-Potenzen"
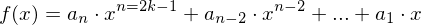
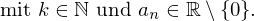
- Die Sinusfunktion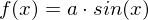 mit beliebigem
mit beliebigem
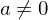 .
.
- Die Nullfunktion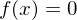 . (Einzige Funktion die sowohl
. (Einzige Funktion die sowohl
gerade, als auch ungerade ist.)
Bemerkungen:
In Worten bedeutet die obige Gleichung: "Betrachtet man
auf der x-Achse eine Zahl und ihre Gegenzahl, so sind auch die entsprechenden y-Werte jeweils Zahl und Gegenzahl."
Ungerade Zahlen haben immer die Form eines Produkt aus einer natürlichen Zahl mit 2 abzüglich oder zuzüglich 1.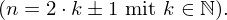
Beachte, dass man die entsprechende Funktion als "ungerade" bezeichnet - nicht aber das Schaubild!
Beispiele:
- Jede Proportionalität
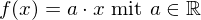 oder
oder allg. Potenzfktn. mit ungerader, ganzzahliger Hochzahl
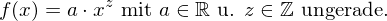 .
. Hierzu zählt auch die Kehrwertfunktion
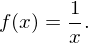
- Jede ganzrationale Funktion mit ausschließlich ungeraden
"x-Potenzen"
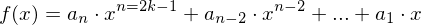
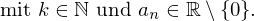
- Die Sinusfunktion
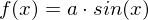 mit beliebigem
mit beliebigem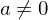 .
.- Die Nullfunktion
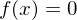 . (Einzige Funktion die sowohl
. (Einzige Funktion die sowohlgerade, als auch ungerade ist.)
Bemerkungen:
In Worten bedeutet die obige Gleichung: "Betrachtet man
auf der x-Achse eine Zahl und ihre Gegenzahl, so sind auch die entsprechenden y-Werte jeweils Zahl und Gegenzahl."
Ungerade Zahlen haben immer die Form eines Produkt aus einer natürlichen Zahl mit 2 abzüglich oder zuzüglich 1.
Tags: Begriffe, Funktion, ganzrational, Symmetrie
Source:
Source:
Finde eine Funktion deren Schaubild an der Stelle 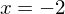 und die x-Achse durchschneidet, an der Stelle
und die x-Achse durchschneidet, an der Stelle 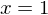 die x-Achse berührt und die y-Achse im Punkt (0/6) schneidet.
die x-Achse berührt und die y-Achse im Punkt (0/6) schneidet.
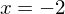 und die x-Achse durchschneidet, an der Stelle
und die x-Achse durchschneidet, an der Stelle 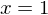 die x-Achse berührt und die y-Achse im Punkt (0/6) schneidet.
die x-Achse berührt und die y-Achse im Punkt (0/6) schneidet.Für die Lösung dieser Aufgabe benötigt man nicht unbedingt die Differenzialrechnung.
Die einfache Nullstelle liefert den Faktor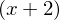 , die doppelte Nullstelle (bei x=1) entsprechend
, die doppelte Nullstelle (bei x=1) entsprechend 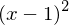 . Hieraus ergibt sich eine (Hilfs-)Funktion
. Hieraus ergibt sich eine (Hilfs-)Funktion 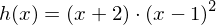 , die wir so in y-Richtung strecken, dass das Schaubild der gestreckten Funktion durch (0/6) verläuft.
, die wir so in y-Richtung strecken, dass das Schaubild der gestreckten Funktion durch (0/6) verläuft. 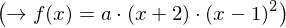
Aus (0/6) folgt: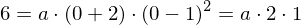
also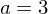 .
.
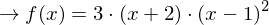
(Bei f(x) handelt es sich um eine ganzrationale Funktion, aber eine Darstellung in Summenform ist nicht gefordert! Kontrolliere das Ergebnis mit dem GTR/CAS.)
Die einfache Nullstelle liefert den Faktor
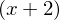 , die doppelte Nullstelle (bei x=1) entsprechend
, die doppelte Nullstelle (bei x=1) entsprechend 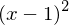 . Hieraus ergibt sich eine (Hilfs-)Funktion
. Hieraus ergibt sich eine (Hilfs-)Funktion 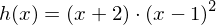 , die wir so in y-Richtung strecken, dass das Schaubild der gestreckten Funktion durch (0/6) verläuft.
, die wir so in y-Richtung strecken, dass das Schaubild der gestreckten Funktion durch (0/6) verläuft. 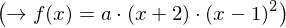
Aus (0/6) folgt:
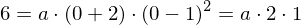
also
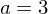 .
.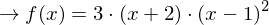
(Bei f(x) handelt es sich um eine ganzrationale Funktion, aber eine Darstellung in Summenform ist nicht gefordert! Kontrolliere das Ergebnis mit dem GTR/CAS.)
Tags: Funktion, ganzrational, Nullstelle, Produktform, Streckung
Source:
Source:
Warum hat eine ganzrationale Funktion vom Grad n höchstens n Nullstellen?
Jede Nullstelle 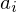 einer ganzrationalen Funktion erzeugt in der Produktform einen Linearfaktor der Form
einer ganzrationalen Funktion erzeugt in der Produktform einen Linearfaktor der Form 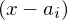 .
.
Gäbe es mehr als n Nullstellen, könnte man die Funktion in der Produktdarstellung mit mehr als n Linearfaktoren darstellen. Beim Ausmultiplizieren wäre hierbei die größte x-Potenz größer als n. Das kann nicht sein.
Beachte: Es gibt natürlich ganzrationale Funktionen vom Grad n mit weniger als n Nullstellen.
Beispiel: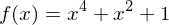 hat gar keine Nullstelle.
hat gar keine Nullstelle.
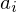 einer ganzrationalen Funktion erzeugt in der Produktform einen Linearfaktor der Form
einer ganzrationalen Funktion erzeugt in der Produktform einen Linearfaktor der Form 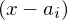 .
. Gäbe es mehr als n Nullstellen, könnte man die Funktion in der Produktdarstellung mit mehr als n Linearfaktoren darstellen. Beim Ausmultiplizieren wäre hierbei die größte x-Potenz größer als n. Das kann nicht sein.
Beachte: Es gibt natürlich ganzrationale Funktionen vom Grad n mit weniger als n Nullstellen.
Beispiel:
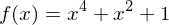 hat gar keine Nullstelle.
hat gar keine Nullstelle.Tags: ganzrational, Grad, Nullstelle
Source:
Source:
Flashcard set info:
Author: www.mathematik-bw.de
Main topic: Mathematik
Topic: 10. Klasse
School / Univ.: Clara-Schumann-Gymnasium
City: Lahr
Published: 23.12.2009
Card tags:
All cards (47)
Ableitung (10)
Änderungsrate (9)
Anwendung (2)
Begriffe (17)
Definitionsmenge (1)
Extremstelle (2)
Funktion (8)
ganzrational (5)
Gerade (13)
Grad (1)
h-Methode (6)
hinreichend (3)
Intervalle (1)
Normale (2)
notwendig (2)
Nullstelle (5)
Produktform (3)
Sattelpunkt (3)
Schnittwinkel (1)
Sekante (1)
Sekantensteigung (1)
Steigungswinkel (3)
Streckung (1)
Symmetrie (3)
Tangente (7)
Terassenpunkt (3)
Verschiebung (7)
Wertemenge (1)



