Welcher Zusammenhang besteht zwischen dem Steigungswinkel einer Geraden und deren Steigung?
Welchen Steigungswinkel hat eine Gerade mit der Steigung 1?
Welche Werte kann ein Steigungswinkel annehmen?
Welchen Steigungswinkel hat eine Gerade mit der Steigung 1?
Welche Werte kann ein Steigungswinkel annehmen?
Mit Hilfe der Tangensbeziehung am rechtwinkligen Dreieck folgt aus dem Steigungsdreieck für den Steigungswinkel 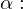
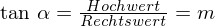 .
.
Bei einer Geraden mit der Steigung eins ist das Verhältnis aus Hochwert zu Rechtswert bei jedem Steigungsdreieck 1. Der Steigungswinkel ist hierbei Basiswinkel eines rechtwinklig gleichschenkligen Dreiecks und somit gleich 45°.
Steigungswinkel können Werte zwischen -90° und +90° annehmen. (Bei +/-90° ist die Geradensteigung nicht definiert, da die Gerade parallel zur y-Achse verläuft - der Rechtswert bei allen Steigungsdreiecken ist hier 0!)
(Lässt man keine negativen Steigungswinkel zu, liegen die Steigungswinkel zwischen 0° und 180°, wobei die Steigungen der Geraden ab 90° negativ verlaufen.)
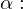
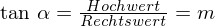 .
.Bei einer Geraden mit der Steigung eins ist das Verhältnis aus Hochwert zu Rechtswert bei jedem Steigungsdreieck 1. Der Steigungswinkel ist hierbei Basiswinkel eines rechtwinklig gleichschenkligen Dreiecks und somit gleich 45°.
Steigungswinkel können Werte zwischen -90° und +90° annehmen. (Bei +/-90° ist die Geradensteigung nicht definiert, da die Gerade parallel zur y-Achse verläuft - der Rechtswert bei allen Steigungsdreiecken ist hier 0!)
(Lässt man keine negativen Steigungswinkel zu, liegen die Steigungswinkel zwischen 0° und 180°, wobei die Steigungen der Geraden ab 90° negativ verlaufen.)
Tags: Begriffe, Gerade, Steigungswinkel
Quelle:
Quelle:
Woran erkennt man bereits an den Punktkoordinaten zweier Geradenpunkte, ob der Steigungswinkel der Geraden negativ ist?
Liegt der y-Wert des rechten Punktes unterhalb des y-Wertes des linken, dann "fällt die Gerade an". Der Steigungswinkel (und die Steigung) ist in diesen Fällen negativ.
Tags: Begriffe, Gerade, Steigungswinkel
Quelle:
Quelle:
Wie bestimmt man den Schnittwinkel zwischen zwei Geraden?
Erstelle zunächst eine Skizze!
Bestimme die Steigungswinkel zu jeder einzelnen Geraden und errechne hieraus den Wert für die Steigungswinkel beider Geraden.
Beachte, dass man je nach Lage der Geraden die Steigungswinkel addieren bzw. voneinander subtrahieren muss. Aus diesem Grund ist bei dieser Aufgabenstellung eine Skizze unbedingt zu empfehlen.
Linktipp: Landesbildungsserver Baden-Württemberg
Bestimme die Steigungswinkel zu jeder einzelnen Geraden und errechne hieraus den Wert für die Steigungswinkel beider Geraden.
Beachte, dass man je nach Lage der Geraden die Steigungswinkel addieren bzw. voneinander subtrahieren muss. Aus diesem Grund ist bei dieser Aufgabenstellung eine Skizze unbedingt zu empfehlen.
Linktipp: Landesbildungsserver Baden-Württemberg
Tags: Begriffe, Gerade, Schnittwinkel, Steigungswinkel
Quelle:
Quelle:
Kartensatzinfo:
Autor: www.mathematik-bw.de
Oberthema: Mathematik
Thema: 10. Klasse
Schule / Uni: Clara-Schumann-Gymnasium
Ort: Lahr
Veröffentlicht: 23.12.2009
Schlagwörter Karten:
Alle Karten (47)
Ableitung (10)
Änderungsrate (9)
Anwendung (2)
Begriffe (17)
Definitionsmenge (1)
Extremstelle (2)
Funktion (8)
ganzrational (5)
Gerade (13)
Grad (1)
h-Methode (6)
hinreichend (3)
Intervalle (1)
Normale (2)
notwendig (2)
Nullstelle (5)
Produktform (3)
Sattelpunkt (3)
Schnittwinkel (1)
Sekante (1)
Sekantensteigung (1)
Steigungswinkel (3)
Streckung (1)
Symmetrie (3)
Tangente (7)
Terassenpunkt (3)
Verschiebung (7)
Wertemenge (1)



