Was versteht man unter "orthogonal"?
Wie lautet die "Orthogonalitätsbedingung" bei Geradensteigungen? Gib die Gleichung an und formuliere den Zusammenhang in einem Satz.
Wo wird die Orthoganlitätsbedingung benötigt?
Wie lautet die "Orthogonalitätsbedingung" bei Geradensteigungen? Gib die Gleichung an und formuliere den Zusammenhang in einem Satz.
Wo wird die Orthoganlitätsbedingung benötigt?
"Orthogonal" ist ein Synonym zu "rechtwinklig".
Die Orthogonalitätsbedingung lautet: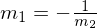
oder 
.
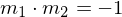Dies bedeutet, dass bei zwei zueinander senkrecht stehenden Geraden die eine Steigung genau die Gegenzahl des Kehrwertes der anderen Steigung ist.
(Z. B. ist zu einer Geraden mit der Steigung 2 jede Gerade orthogonal, die die Steigung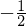
besitzt.)
Die Orthogonalitätsbediung wird beim Zusammenhang von Tangenten und Normalen benötigt.
Die Orthogonalitätsbedingung lautet:
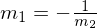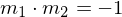oder .Dies bedeutet, dass bei zwei zueinander senkrecht stehenden Geraden die eine Steigung genau die Gegenzahl des Kehrwertes der anderen Steigung ist.
(Z. B. ist zu einer Geraden mit der Steigung 2 jede Gerade orthogonal, die die Steigung
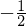besitzt.)Die Orthogonalitätsbediung wird beim Zusammenhang von Tangenten und Normalen benötigt.
Tags: Gerade, Normale, Tangente
Quelle:
Quelle:
Wie lauten die Gleichungen der Tangenen und der Normalen an die Normalparabel an der Stelle x=1,5?
Zugehörige Funktion: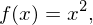 
Tangentensteigung aus Ableitungsfunktion 
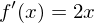somit beträgt die Tangentsteigung an der Stelle 1,5: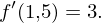 
Der y-Wert an der Stelle 1,5 ist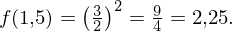
Verschiebt man eine Ursprungsgerade mit der Steigung 3 um 1,5 in x-Richtung und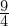
in y-Richtung erhält man die gesuchte Tangente. Ihre Gleichung lautet:
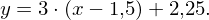
Aufgrund der Orthogonalitätsbedingung folgt für die Gleichung der zugehörigen Normalen:
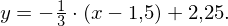
Hinweis:
In der Hauptform (mit Steigung und y-Achsenabschnitt) lauten die Gleichungen:
Tangente: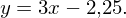
Normale: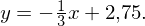
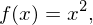Tangentensteigung aus Ableitungsfunktion 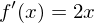somit beträgt die Tangentsteigung an der Stelle 1,5: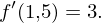 Der y-Wert an der Stelle 1,5 ist
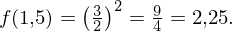
Verschiebt man eine Ursprungsgerade mit der Steigung 3 um 1,5 in x-Richtung und
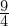in y-Richtung erhält man die gesuchte Tangente. Ihre Gleichung lautet: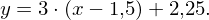 Aufgrund der Orthogonalitätsbedingung folgt für die Gleichung der zugehörigen Normalen:
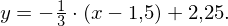
Hinweis:
In der Hauptform (mit Steigung und y-Achsenabschnitt) lauten die Gleichungen:
Tangente:
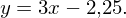
Normale:
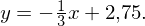
Tags: Gerade, Normale, Tangente, Verschiebung
Quelle:
Quelle:
Kartensatzinfo:
Autor: www.mathematik-bw.de
Oberthema: Mathematik
Thema: 10. Klasse
Schule / Uni: Clara-Schumann-Gymnasium
Ort: Lahr
Veröffentlicht: 23.12.2009
Schlagwörter Karten:
Alle Karten (47)
Ableitung (10)
Änderungsrate (9)
Anwendung (2)
Begriffe (17)
Definitionsmenge (1)
Extremstelle (2)
Funktion (8)
ganzrational (5)
Gerade (13)
Grad (1)
h-Methode (6)
hinreichend (3)
Intervalle (1)
Normale (2)
notwendig (2)
Nullstelle (5)
Produktform (3)
Sattelpunkt (3)
Schnittwinkel (1)
Sekante (1)
Sekantensteigung (1)
Steigungswinkel (3)
Streckung (1)
Symmetrie (3)
Tangente (7)
Terassenpunkt (3)
Verschiebung (7)
Wertemenge (1)
