Finde eine Funktion deren Schaubild an der Stelle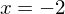 
und die x-Achse durchschneidet, an der Stelle 
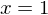die x-Achse berührt und die y-Achse im Punkt (0/6) schneidet.
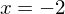und die x-Achse durchschneidet, an der Stelle 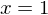die x-Achse berührt und die y-Achse im Punkt (0/6) schneidet.Für die Lösung dieser Aufgabe benötigt man nicht unbedingt die Differenzialrechnung.
Die einfache Nullstelle liefert den Faktor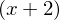
, die doppelte Nullstelle (bei x=1) entsprechend 
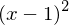. Hieraus ergibt sich eine (Hilfs-)Funktion 
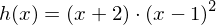, die wir so in y-Richtung strecken, dass das Schaubild der gestreckten Funktion durch (0/6) verläuft.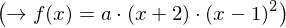 
Aus (0/6) folgt: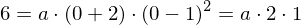
also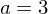
.
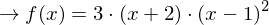
(Bei f(x) handelt es sich um eine ganzrationale Funktion, aber eine Darstellung in Summenform ist nicht gefordert! Kontrolliere das Ergebnis mit dem GTR/CAS.)
Die einfache Nullstelle liefert den Faktor
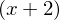, die doppelte Nullstelle (bei x=1) entsprechend 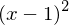. Hieraus ergibt sich eine (Hilfs-)Funktion 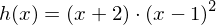, die wir so in y-Richtung strecken, dass das Schaubild der gestreckten Funktion durch (0/6) verläuft.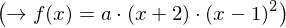 Aus (0/6) folgt:
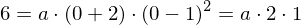
also
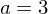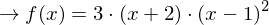
.(Bei f(x) handelt es sich um eine ganzrationale Funktion, aber eine Darstellung in Summenform ist nicht gefordert! Kontrolliere das Ergebnis mit dem GTR/CAS.)
Tags: Funktion, ganzrational, Nullstelle, Produktform, Streckung
Quelle:
Quelle:
Kartensatzinfo:
Autor: www.mathematik-bw.de
Oberthema: Mathematik
Thema: 10. Klasse
Schule / Uni: Clara-Schumann-Gymnasium
Ort: Lahr
Veröffentlicht: 23.12.2009
Schlagwörter Karten:
Alle Karten (47)
Ableitung (10)
Änderungsrate (9)
Anwendung (2)
Begriffe (17)
Definitionsmenge (1)
Extremstelle (2)
Funktion (8)
ganzrational (5)
Gerade (13)
Grad (1)
h-Methode (6)
hinreichend (3)
Intervalle (1)
Normale (2)
notwendig (2)
Nullstelle (5)
Produktform (3)
Sattelpunkt (3)
Schnittwinkel (1)
Sekante (1)
Sekantensteigung (1)
Steigungswinkel (3)
Streckung (1)
Symmetrie (3)
Tangente (7)
Terassenpunkt (3)
Verschiebung (7)
Wertemenge (1)
