Was ist der einfachste Verrechnungsmodus (Methode der Skalierung)? Welche Bedingung muss gelten, damit dieser Verrechnungsmodus fair ist?
Der einfachste Verrechnungsmodus sieht als Testkennwert die Anzahl gelöster Aufgaben vor. Das heißt, ungeachtet dessen, welche Aufgaben von einer Tp gelöst und welche nicht gelöst werden, zählen nur die "Treffer".
Fischer gibt dazu einen Beweis, wonach das (dichotome) logistische Testmodell von Georg Rasch - Rasch-Modell - notwendigerweise gelten muss, damit dieser Verrechnungsmodus fair ist.
Das Rasch-Modell beschreibt die Wahrscheinlichkeit, dass Tp Item
Item  löst (+), in Abhängigkeit des Personenparameters
löst (+), in Abhängigkeit des Personenparameters 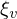 , das ist die (wahre) Fähigkeit von
, das ist die (wahre) Fähigkeit von  , und des Itemparameters
, und des Itemparameters 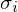 , das ist die (wahre) Schwierigkeit von
, das ist die (wahre) Schwierigkeit von  :
:

Weil sich dieses Modell als im statistischen Sinn stichprobenunabhängig herausstellt, kann auch ein besonderer Modelltest abgeleitet werden - somit muss es nie ungeprüft vorausgesetzt werden.
Fischer gibt dazu einen Beweis, wonach das (dichotome) logistische Testmodell von Georg Rasch - Rasch-Modell - notwendigerweise gelten muss, damit dieser Verrechnungsmodus fair ist.
Das Rasch-Modell beschreibt die Wahrscheinlichkeit, dass Tp
 Item
Item  löst (+), in Abhängigkeit des Personenparameters
löst (+), in Abhängigkeit des Personenparameters 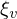 , das ist die (wahre) Fähigkeit von
, das ist die (wahre) Fähigkeit von  , und des Itemparameters
, und des Itemparameters 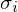 , das ist die (wahre) Schwierigkeit von
, das ist die (wahre) Schwierigkeit von  :
:
Weil sich dieses Modell als im statistischen Sinn stichprobenunabhängig herausstellt, kann auch ein besonderer Modelltest abgeleitet werden - somit muss es nie ungeprüft vorausgesetzt werden.
Tags: Rasch-Modell, Skalierung, Stichprobenunabhängig
Source: S88
Source: S88
Inwiefern ist das Rasch-Modell stichprobenunabhängig?
Im Gegensatz zu anderen testtheoretischen Modellen erfüllt das Rasch-Modell" einen besonderen wissenschaftstheoretischen Ansatz, nämlich den sog. "spezifisch objektive" Vergleiche zu ermöglichen:
Den Unterschied in den Fähigkeiten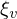 und
und 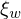 zwischen je zwei Personen
zwischen je zwei Personen  und
und 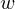 kann unabhängig davon bestimmt werden, welche Aufgaben des Tests herangezogen werden; bzw. umgekehrt und wichtiger, der Vergleich je zweier Aufgaben
kann unabhängig davon bestimmt werden, welche Aufgaben des Tests herangezogen werden; bzw. umgekehrt und wichtiger, der Vergleich je zweier Aufgaben  und
und 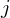 bezüglich
bezüglich 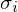 und
und 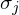 ist unabhängig davon mögliche, welche Stichprobe dafür verwendet wird.
ist unabhängig davon mögliche, welche Stichprobe dafür verwendet wird.
Das heißt, die Schätzung der Parameter sind insofern stichprobenunabhängig, als die Wahl der Stichprobe aus einer bestimmten Population für die statistische Interferenz dieser Parameter keine Rolle spielt.
Diese Tatsache kann für den Spezialfall eines Tests mit nur zwei Aufgaben leicht bewiesen werden, und zwar ausgehend vom zitierten Beweis, wonach bei Geltung des Rasch-Modells die Anzahl gelöster Aufgaben (S) einen fairen Testkennwert darstellt.
Stellt sich dementsprechend einmal empirisch heraus, dass (abgesehen von zufallsbedingten Variationen) die Differenz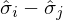 von Stichprobe zu Stichprobe verschieden ist, so stünde das in Widerspruch zu der abgeleiteten Konsequenz des Rasch-Modells; was heißt: Das Rasch-Modell kann nicht gelten - folglich wäre die zur Diskussion stehende Verrechnung nicht fair.
von Stichprobe zu Stichprobe verschieden ist, so stünde das in Widerspruch zu der abgeleiteten Konsequenz des Rasch-Modells; was heißt: Das Rasch-Modell kann nicht gelten - folglich wäre die zur Diskussion stehende Verrechnung nicht fair.
Den Unterschied in den Fähigkeiten
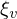 und
und 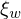 zwischen je zwei Personen
zwischen je zwei Personen  und
und 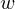 kann unabhängig davon bestimmt werden, welche Aufgaben des Tests herangezogen werden; bzw. umgekehrt und wichtiger, der Vergleich je zweier Aufgaben
kann unabhängig davon bestimmt werden, welche Aufgaben des Tests herangezogen werden; bzw. umgekehrt und wichtiger, der Vergleich je zweier Aufgaben  und
und 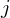 bezüglich
bezüglich 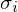 und
und 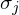 ist unabhängig davon mögliche, welche Stichprobe dafür verwendet wird.
ist unabhängig davon mögliche, welche Stichprobe dafür verwendet wird.Das heißt, die Schätzung der Parameter sind insofern stichprobenunabhängig, als die Wahl der Stichprobe aus einer bestimmten Population für die statistische Interferenz dieser Parameter keine Rolle spielt.
Diese Tatsache kann für den Spezialfall eines Tests mit nur zwei Aufgaben leicht bewiesen werden, und zwar ausgehend vom zitierten Beweis, wonach bei Geltung des Rasch-Modells die Anzahl gelöster Aufgaben (S) einen fairen Testkennwert darstellt.
Stellt sich dementsprechend einmal empirisch heraus, dass (abgesehen von zufallsbedingten Variationen) die Differenz
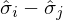 von Stichprobe zu Stichprobe verschieden ist, so stünde das in Widerspruch zu der abgeleiteten Konsequenz des Rasch-Modells; was heißt: Das Rasch-Modell kann nicht gelten - folglich wäre die zur Diskussion stehende Verrechnung nicht fair.
von Stichprobe zu Stichprobe verschieden ist, so stünde das in Widerspruch zu der abgeleiteten Konsequenz des Rasch-Modells; was heißt: Das Rasch-Modell kann nicht gelten - folglich wäre die zur Diskussion stehende Verrechnung nicht fair. Tags: Rasch-Modell, stichprobenunabhängig
Source: S89
Source: S89
Flashcard set info:
Author: coster
Main topic: Psychologie
Topic: Psychologische Diagnostik
School / Univ.: Universität Wien
City: Wien
Published: 12.06.2013
Tags: SS2013, Holocher-Ertl
Card tags:
All cards (119)
16 PF-R (3)
AIST-R/UST-R (2)
Aufmerksamkeit (1)
Beobachten (1)
Big Five (1)
culture-fair (5)
Definition (3)
Diagnostik (15)
Eichmaßstäbe (3)
Eichung (9)
Eigenschaft (1)
Ethik (1)
Fairness (7)
Faktorenanalyse (2)
Formal (8)
Fragen (3)
Freiwillige (1)
GIS (1)
Grundsätze (6)
Gruppenverfahren (1)
Gütekriterien (1)
Intelligenz (1)
Interessen (4)
IQ (1)
Konzentration (1)
Laien (1)
Leistungsdiagnostik (13)
Memory (1)
Merkmal (1)
Messen (1)
NEO-PI-R (2)
Nützlichkeit (2)
Objektivität (5)
Ökonomie (3)
Postkorb (1)
Profil (1)
Prognose (1)
Prozentrang (2)
Prüfen (3)
Psychologe (1)
Rasch-Modell (5)
Reasoning (1)
Reliabilität (6)
Schwierigkeit (1)
Skalierung (8)
Space (1)
Stichprobenunabhängig (1)
Test (2)
trait (1)
Validität (8)
Verfahren (3)
Voraussetzung (1)
Zumutbarkeit (2)



