Was ist Mustererkennung? Was versteht man darunter?
Mustererkennung
Beispiel:
Der Computer soll Sprache ähnlich zuverlässig erkennen wie ein Mensch...was aber nicht unbedingt auf dem gleichen Weg geschehen muss.
- betreffen mathematisch-technische Aspekte der Perzeption / Wahrnehmung anhand von Sensordaten
- => Simulation einer perzeptiven Leistung (ähnlich Mensch)
- automatische Transformation eines Sensorsignals in einer aufgabenspezifische Beschreibung
- => es wird für ein physikalisches Signal (Sprache,Bild, Messwert, ...) eine geeignete Sympolkette (Datenstruktur) berechnet.
- Dabei unterteilt man in zwei Kategorien:
- Klassifikation einfacher Muster
- Analyse komplexer Muster
Beispiel:
Der Computer soll Sprache ähnlich zuverlässig erkennen wie ein Mensch...was aber nicht unbedingt auf dem gleichen Weg geschehen muss.
Was ist ein Muster? Wie ist es definiert?
Muster
Ein Muster kann ein ganzes Bild sein oder z.B. aus mehreren Bilder bestehen (Schnittbilder in Exprimage)..
Beispiele:
Schnittbilder in Exprimage:
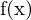 = (HE1, VIM, ER, PR, ... , Grading, Therapie, Verlauf, ...)
= (HE1, VIM, ER, PR, ... , Grading, Therapie, Verlauf, ...)
Farbbild aus TV als Muster (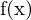 ,
, 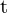 = Zeitpunkt):
= Zeitpunkt):
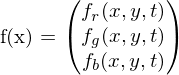
- die Elemente der Menge U, die zu einem Problemkreis
 gehören
gehören - Muster heißen Funktionen
- dargestellt durch MxN Funktionen
- Funktionen können den zugeordneten Merkmalen entsprechen
- es gibt komplexe und einfache Muster
Ein Muster kann ein ganzes Bild sein oder z.B. aus mehreren Bilder bestehen (Schnittbilder in Exprimage)..
Beispiele:
Schnittbilder in Exprimage:
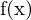 = (HE1, VIM, ER, PR, ... , Grading, Therapie, Verlauf, ...)
= (HE1, VIM, ER, PR, ... , Grading, Therapie, Verlauf, ...) Farbbild aus TV als Muster (
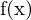 ,
, 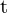 = Zeitpunkt):
= Zeitpunkt):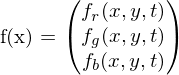
Was sind Klassen? Welche Eigenschaften haben sie?
Klassen (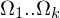 )
)
Klassen sind Partitionen der Menge in k Teilmengen und sollten folgende Eigenschaften erfüllen:
in k Teilmengen und sollten folgende Eigenschaften erfüllen:
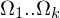 )
)Klassen sind Partitionen der Menge
 in k Teilmengen und sollten folgende Eigenschaften erfüllen:
in k Teilmengen und sollten folgende Eigenschaften erfüllen:- die Vereinigung aller Mengen
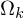 ist
ist 
- keine Menge ist leer
- keine disjunkten Mengen (keine Eigenschaften/Muster doppelt in einer Klasse)
- Wenn die Merkmale des Musters bestimmte Eigenschaften haben werden sie einer Klasse zugeordnet.
- Muster einer Klasse sollten ähnlich untereinander und verschieden zu anderen Mustern anderer Klassen sein
- eine Definition von Ähnlichkeit (Abstandsmaß/Klassifikator) wird vorausgsetzt
- wenn ein Muster nicht zuverlässig klassifiziert werden kann => entfernen in Rückweisungsklasse
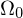 oder Alternativen angeben (Mischklassen)
oder Alternativen angeben (Mischklassen)
Was ist ein einfaches Muster?
Einfache Muster:
Definition: Ein Muster wird als einfaches Muster bezeichnet, wenn den Anwender nur der Klassenname interessiert und es möglich ist, es als Ganzes genau einer Klasse zuzuweisen.
Bei einfachen Mustern spricht man von Klassifikation.
Beispiele:
=> es ist nur der Klassenname von Interesse
Definition: Ein Muster wird als einfaches Muster bezeichnet, wenn den Anwender nur der Klassenname interessiert und es möglich ist, es als Ganzes genau einer Klasse zuzuweisen.
Bei einfachen Mustern spricht man von Klassifikation.
Beispiele:
- Farbbild aus TV
- einzelnes gesondertes Schriftzeichen
- isoliert gesprochenes Wort
- Gewebetyp
- ....
=> es ist nur der Klassenname von Interesse
Was ist ein komplexes Muster?
Komplexe Muster
Definition: Ein Muster wird als komplexes Muster bezeichnet, wenn dem Anwender die Angabe eines Klassennamens nicht genügt oder wenn die Klassifikation als ganzes in eine Klasse nicht möglich ist.
Der Übergang zwischen einfachen Mustern und komplexen Mustern ist fließend.
Bei komplexen Mustern spricht man von Analyse der Muster. Es geht dabei meistens um komplexere Szenarien. Die Klassifikation als Ganzes in genau eine Klasse ist nicht möglich.
Beispiele:

Definition: Ein Muster wird als komplexes Muster bezeichnet, wenn dem Anwender die Angabe eines Klassennamens nicht genügt oder wenn die Klassifikation als ganzes in eine Klasse nicht möglich ist.
Der Übergang zwischen einfachen Mustern und komplexen Mustern ist fließend.
Bei komplexen Mustern spricht man von Analyse der Muster. Es geht dabei meistens um komplexere Szenarien. Die Klassifikation als Ganzes in genau eine Klasse ist nicht möglich.
Beispiele:
- Exprimage:
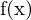 = (HE1, VIM, ER, PR, ... , Grading, Therapie, Verlauf, ...)
= (HE1, VIM, ER, PR, ... , Grading, Therapie, Verlauf, ...) - Verkehrszenen
- Diagnostische Interpretation von Bildern
- ....

Was bedeutet Klassifikation einfacher Muster?
Klassifikationsaufgaben können sowohl bei einfachen als auch bei komplexen Mustern auftreten.
Klassifikation von einfachen Mustern:
Bei der Klassifikation von einfachen Mustern wird jedes Muster als ein ganzes betrachtet und unabhängig genau einer Klasse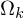 von k möglichen Klassen zugeordnet.
von k möglichen Klassen zugeordnet.
Das Muster kann auch in eine Klasse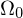 zurückgewiesen werden.
zurückgewiesen werden.
Beispiel: Klassifikation von einzelnen Schriftzeichen

Klassifikation von einfachen Mustern:
Bei der Klassifikation von einfachen Mustern wird jedes Muster als ein ganzes betrachtet und unabhängig genau einer Klasse
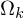 von k möglichen Klassen zugeordnet.
von k möglichen Klassen zugeordnet. Das Muster kann auch in eine Klasse
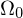 zurückgewiesen werden.
zurückgewiesen werden.Beispiel: Klassifikation von einzelnen Schriftzeichen

Was bedeuetet Analyse komplexer Muster?
Ein komplexes Muster (z.B. Exprimage => mehrere Daten zu einem bisher unverstandenen Krankheitsverlauf) kann in der Regel mehr als ein zu klassifizierendes Objekt enthalten.
Ein Muster muss im Kontext zu anderen Mustern klassifiziert werden ... => bei der Analyse komplexer Muster wird jedem Muster eine individuelle symbolische Beschreibung zugeordnet.
Das Muster wird aufgrund einer Wissensbasis (z.B. gelabelte Daten) bzw. eines Modells errechnet.
Diagnoseunterstützung von komplexen Krankheiten (Krebs)
Ein Muster muss im Kontext zu anderen Mustern klassifiziert werden ... => bei der Analyse komplexer Muster wird jedem Muster eine individuelle symbolische Beschreibung zugeordnet.
Das Muster wird aufgrund einer Wissensbasis (z.B. gelabelte Daten) bzw. eines Modells errechnet.
Diagnoseunterstützung von komplexen Krankheiten (Krebs)
Woher kommen die Klasseneinteilungen?
1. Ansicht (objektive Betrachtungsweise)
2. Experimentelle Realität
3. Ähnlichkeiten
Algorithmische Möglichkeiten:
- Aussagekräftige Konzepte
- Kategorisierung (gemeinsame Eigenschaften in eine Kategorie)
2. Experimentelle Realität
- Menschliche Wahrnehmung nachempfinden
- Wahrnehmung
- Bewegung eines Körpers
- Erfahrung (physikalisch und soziel) => Heuristiken
- prototypenbasierte Kategorien (definiert durch kognitives Modell) => z.B. Modell
3. Ähnlichkeiten
- Existenz einer realen Umgebung
- stabiles Wissen über die Welt
- Realität limitiert diese Konzepte
Algorithmische Möglichkeiten:
- supervisierten Lernen
- unsupervisierten Lernen
Was ist supervisiertes Lernen?
Es werden vom Menschen gelabelte Daten (z.B. Das ist Tumor, das ist Entzündung, ...) von Stichproben vorgegeben, an denen sich ein Klassifikator orientiert => Training eines Klassifikators
Algorithmen zum Training eines Klassifikators:
Algorithmen zum Training eines Klassifikators:
- Supported Vector Machine
- Random Forests
- Neuronale Netze
Was ist unsupervisiertes Lernen?
Es wird versucht anhand von mehrdimensionalen gegebenen Daten eine Ordnung der Daten zu berechnen ohne dass Vorwissen über die Daten vorhanden ist. Es geht dabei lediglich um eine Differenzierung der Daten (z.B. visualisiert durch Segmentierung (Exprimage SOM)), nicht um eine Erkennung. Es gibt keine Stichproben mit gelabelten Daten. Es wird nur anhand der momentanen Datenbasis versucht eine Ordnung zu finden.
=> Erstellen von homogenen Teilmengen (Clustern)
Clustering-Algorihtmen
=> Erstellen von homogenen Teilmengen (Clustern)
Clustering-Algorihtmen
- K-Mean-Clustering
- Self-Organizing-Map (SOM), Neuronale Netze
- Histogrammbasierte Clusteranalyse
Was ist der Unterschied zwischen Maschinellen Lernen und Data-Maining?
Maschinelles Lernen:
finden von bekannten Mustern in neuen Daten
Data-Mining (Daten schürfen):
finden neuer unbekannter Muster (Zusammenhänge) aufgrund großer Datenmengen
Beide Vorgehensweisen verfolgen das Ziel der Mustererkennung.
finden von bekannten Mustern in neuen Daten
Data-Mining (Daten schürfen):
finden neuer unbekannter Muster (Zusammenhänge) aufgrund großer Datenmengen
Beide Vorgehensweisen verfolgen das Ziel der Mustererkennung.
Stichproben?
1. Informationen über Problemkreis  sammeln
sammeln
=> Randfälle finden
=> Interessante Fälle finden
 sammeln
sammeln- repräsentative Stichproben
- Generalisierung von Beobachtungen => Konfidenzintervall (Vertrauenbereich) Er sagt etwas über die Präzision der Lageschätzung eines Parameters (zum Beispiel eines Mittelwertes) aus.
- Stichproben sollten möglichst disjunkt sein
=> Randfälle finden
=> Interessante Fälle finden
Kompaktheit?
3. Kompaktheit
Die Merkmale bilden für Muster einer Klasse einen einigermaßen kompakten Bereich im Merkmalsraum => trennen Klassen gut
=> Kompaktheitshypothese
Die Anzahl der Features sollte nicht zu groß sein
=> da "course-of-dimension" (exponentieller Volumenzuwachs des Suchraumes durch Dimensionsvergrößerung)
=> Aussagekräftige Features bestimmen (z.B über PCA)

Die Merkmale bilden für Muster einer Klasse einen einigermaßen kompakten Bereich im Merkmalsraum => trennen Klassen gut
=> Kompaktheitshypothese
Die Anzahl der Features sollte nicht zu groß sein
=> da "course-of-dimension" (exponentieller Volumenzuwachs des Suchraumes durch Dimensionsvergrößerung)
=> Aussagekräftige Features bestimmen (z.B über PCA)

Segmentierungsobject?
4. Segmentierungsobjekt
Ein (komplexes) Muster besitzt einfachere Bestandteile, die untereinander bestimmte Beziehungen haben. Das Muster lässt sich in diese Bestandteile zerlegen.
Übergang von unstrukturierten Pixelmengen => interpretierbaren Objekten
Segmentieren der Bilddaten (Abstrahieren und Zusammenfassen der gegebenen Daten/Informationen)
Beispiel:
Anwendung der SOM => komprimiert verschiedene Hormon-Färbungen zu einem aussagekräftigen Bild.
Ein (komplexes) Muster besitzt einfachere Bestandteile, die untereinander bestimmte Beziehungen haben. Das Muster lässt sich in diese Bestandteile zerlegen.
Übergang von unstrukturierten Pixelmengen => interpretierbaren Objekten
Segmentieren der Bilddaten (Abstrahieren und Zusammenfassen der gegebenen Daten/Informationen)
Beispiel:
Anwendung der SOM => komprimiert verschiedene Hormon-Färbungen zu einem aussagekräftigen Bild.
Strukturen?
5. Strukturen
Ein (komplexes) Muster aus einem Problemkreis hat eine bestimmte Struktur. Das bedeutet, dass nicht jede beliebige Anordnung einfacherer Bestandteile ein Muster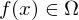 ergibt.
ergibt.
Muster lassen sich mit relativ wenigen einfacheren Bestandteilen darstellen.
=> nicht jede Anordnung eines Musters ist erlaubt!
Beispiel: In der Medizin weiß man, dass der Schädel sich nicht am Fuß befindet.
=> Vorwissen über gegebene Strukturen wird benötigt und kann verwendet werden.
"nachts ist es kälter als draußen" => macht keinen Sinn! => ungültiges Muster!
Ein (komplexes) Muster aus einem Problemkreis hat eine bestimmte Struktur. Das bedeutet, dass nicht jede beliebige Anordnung einfacherer Bestandteile ein Muster
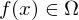 ergibt.
ergibt.Muster lassen sich mit relativ wenigen einfacheren Bestandteilen darstellen.
=> nicht jede Anordnung eines Musters ist erlaubt!
Beispiel: In der Medizin weiß man, dass der Schädel sich nicht am Fuß befindet.
=> Vorwissen über gegebene Strukturen wird benötigt und kann verwendet werden.
"nachts ist es kälter als draußen" => macht keinen Sinn! => ungültiges Muster!
Vorverarbeitung? Was passiert da ... aus welchen Schritten kann die Vorverarbeitung bestehen?
Ein vorgegbenes Muster f wird in ein anderes Muster f´ überführt, dass für die weitere Verarbeitung besser geeignet ist oder/und den Prozess vereinfacht.
Die Segmentierung (Strukturierung/Verdichtung der Daten) kann als eigener Schritt vor der Merkmalsgewinnung eingesetzt werden.
- Kodierung
- Schwellwertoperationen
- Lineare Operationen
- Nicht-Lineare-Operationen
- Normierungsmaßnahmen
- Operationen auf diskreten Mustern
Die Segmentierung (Strukturierung/Verdichtung der Daten) kann als eigener Schritt vor der Merkmalsgewinnung eingesetzt werden.
Kodierung?

Ein Muster hat in der Regel einen kontinuierlichen Definitionsbereich und einen kontinuierlichen Amplitudenbereich (Wertebereich). Für die effektive Darstellung von Mustern in einer für den digitalen Rechner geeigneten Form ergeben sich drei wesentliche Probleme:
1.Abtastung/Sampling: Wieviele Abtastwerte braucht man um zur angemessenen Darstellung des Musters bzw. wie groß muss das Abtastintervall sein?
2. Quantisierung: Wieviele Quantisierungsstufen braucht man zur angemessenen Darstellung der Funktionswerte? => wie muss die Bittiefe eingestellt werden?
3. Wie sollten die Abstufungen in der Quantisierung gewählt werden (linear,logarithmisch,....?)
Wie muss ich abtasten, dass ich das Signal korrekt wieder herstellen kann?
Sampling: Abtasttheorem (Vorverarbeitung, Kodierung)
Sampling: Abtasttheorem (Vorverarbeitung, Kodierung)

Abtasttheorem
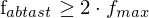 oder im allgemeinen Fall
oder im allgemeinen Fall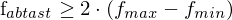 .
.Die praktische Interpretation des Abtasttheorems bedeutet, dass man nur vor der Abtastung die maximale Frequenz kennen oder herausfinden muss (z.B. mit Hilfe der Fourier-Analyse) und das Signal zum Zweck der Digitalisierung mit mehr als der doppelten Frequenz abgetastet werden muss, wenn man das Signal in einer korrekten und guten Näherung rekonstruieren will (ohne Fehler => unendlicher Aufwand).
=> Nyquist-Shannon-Abtasttheorem =
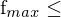
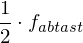 (Nyquist-Frequenz)
(Nyquist-Frequenz)=> wird das Theorem nicht eingehalten kommt es zu Aliasing (siehe Bild) und das Signal kann nicht korrekt wiederhergestellt werden.
Wie verläuft die Quantisierung?
(Kodierung, Vorverarbeitung)
(Kodierung, Vorverarbeitung)

Quantisierungsstufe (s) =
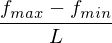
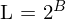 , B = Anzahl Bits, die zur Verfügung stehen
, B = Anzahl Bits, die zur Verfügung stehenBeispiel (Skalare lineare Quantisierung bei Farbbildern 16Bit-Farbtiefe => 8Bit Farbtiefe quantisieren):
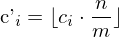
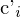 = neue Farbzuordnung
= neue Farbzuordnung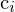 = alte Farbzuordnung
= alte Farbzuordnung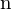 = neue Anzahl Quantisierungsstufen (z.B. 8Bit)
= neue Anzahl Quantisierungsstufen (z.B. 8Bit)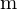 = alte Anzahl Quantisierungsstufen (z.B. 16Bit)
= alte Anzahl Quantisierungsstufen (z.B. 16Bit)Schwellwertoperationen?
Die Auswahl einiger und die Unterdrückung der restlichen Funktionswerte.
Geeignet für einfache Bilder, die auf einem sich stark abhebenden Hintergrund aufgenommen wurden (Beispiel: Gussteil vor Detektorplatte, .. Teile auf Förderband).
Binärisierung:
Geeignet für einfache Bilder, die auf einem sich stark abhebenden Hintergrund aufgenommen wurden (Beispiel: Gussteil vor Detektorplatte, .. Teile auf Förderband).
Binärisierung:
- Verfahren von Otsu
- Schnitt von zwei Gaußfunktionen/Normalverteilungen
- Adaptive-Histogram-Thresholding (Integralbild)
- Maximum-Entropie-Schwellwert
Wie berechnet man einen Schwellwert mittels Schnittpunkt von zwei Normalverteilungen? Wie kann man ein Histogramm durch zwei Gaussfunktionen approximieren?

Ziel: man approximiert durch zwei Gaussfunktionen das Histogramm => bei Schnittpunkt liegt der gesuchte Schwellwert!
Algorithmus:
1. initialen Schwellwert
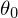 (
(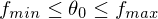 , z.B. 128 bei 8Bit (256 Grauwerten)) setzen
, z.B. 128 bei 8Bit (256 Grauwerten)) setzen2. Wiederhole
- berechne
 (links von
(links von 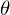 ) und
) und  (rechts von
(rechts von 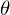 )
) - berechne
 aus Verhältnis beider Gaussfunktionen (zur Normierng
aus Verhältnis beider Gaussfunktionen (zur Normierng  )
) - berechne Fehler zwischen Approximation und Histogramm (z.B. quadratischen Fehler)
- verschiebe
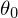 bis
bis 
3.
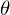 mit minimalen Fehler => Schwellwert (gefunden)
mit minimalen Fehler => Schwellwert (gefunden)- funktioniert gut bei bimodalen Histogrammen (z.B. homogenes Objekt auf homogenen Hintergrund)
- funktioniert nicht bei unimodalen Histogrammen (nur ein Peak => dann besser Schwellwert aus relativem Maximum und erstem verschwindenden Wert im Histogramm bestimmen
Wie funktioniert Adaptive-Histogram-Thresholding? Wie kann man mittels eines Integralbildes binärisieren?
(Vorverarbeitung, Schwellwerte)
(Vorverarbeitung, Schwellwerte)
Adaptive-Histogram-Thresholding
Integralbild = SAT (Summed-Area-Table)
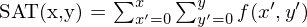
Algorithmus:
1. Berechne Integralbild (SAT)
2. Berechne Mittelwert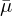 in
in 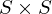 Nachbarschaft von SAT
Nachbarschaft von SAT
Funktioniert auch zur Einteilung von mehreren Pixelklassen (nicht nur binär sondern z.B. 5 Abstufungen)
Integralbild = SAT (Summed-Area-Table)
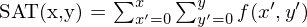
Algorithmus:
1. Berechne Integralbild (SAT)
2. Berechne Mittelwert
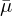 in
in 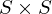 Nachbarschaft von SAT
Nachbarschaft von SAT- wenn Intensität des betrachteten Pixels in der SAT t Prozent höher ist als
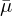 => setze Pixel auf 1
=> setze Pixel auf 1 - sonst => setze Pixel auf 0
Funktioniert auch zur Einteilung von mehreren Pixelklassen (nicht nur binär sondern z.B. 5 Abstufungen)
Binärisierung mittels Entropie .. wie funktioniert das? Wie funktioniert das Maximum-Entropie-Schwellwertverfahren?
(Vorverarbeitung, Schwellwerte)
(Vorverarbeitung, Schwellwerte)
Maximum-Entropie-Schwellwertverfahren
Algorithmus:
1. initialisieren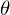 bei
bei 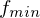 in Histogramm
in Histogramm
2. Iteriere über alle Bins im Histogramm (man schiebt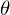 von links
von links 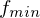 einzeln bis
einzeln bis 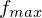 )
)
3. nach Iterationen wähle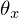 mit
mit 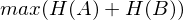
Algorithmus:
1. initialisieren
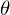 bei
bei 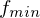 in Histogramm
in Histogramm2. Iteriere über alle Bins im Histogramm (man schiebt
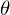 von links
von links 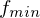 einzeln bis
einzeln bis 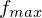 )
)- berechne und speichere Entropie
 von beiden Klassen links von
von beiden Klassen links von  und rechts von
und rechts von  ((Vorder- und Hintergrund) für jedes
((Vorder- und Hintergrund) für jedes 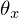
3. nach Iterationen wähle
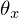 mit
mit 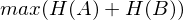
- funktioniert nur bei bimodalen Histogrammen gut (Objekte auf Hintergrund)
- es wird versucht die Entropie zwisch den beiden Klassen (Vorder- und Hintergrund) zu maximieren, so dass jede Klasse ein maximal viel Information ohne die andere Klasse hat => Informationen im Vordergrund und Informationen im Hintergrund
- lässt sich auf für mehrere Schwellwerte (Grauwerabstufung z.B. 256 => 5) einsetzen
Was ist die Wasserscheide-Transformation bzw. der Watershed-Algorithmus und wie funktioniert er?
(Vorverarbeitung, Segmentierung)
(Vorverarbeitung, Segmentierung)

Idee:
- Regen fällt auf eine Landschaft (Pixelintensitäten als Gebirge) und füllt langsam die Löcher, die zu Seen werden
- dazwischen liegen die Wasserscheiden / Dämme
- => Segmente sind die entandenen Seen
Anwendung:
- auf Gradientenbilder
- oder direkt auf Intensitätsbilder
Algorithmus
1. Lese Bild
2. sortiere Pixelwerte bzw. Pixelpositionen nach Grauwerten (z.B. 256-linked-lists)
3. initialisiere Regionen-Bild mit Labeln
4. Für alle Wasser-Level
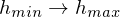
Wiederhole
- flute Pixel, die bereits geflutete Nachbarn haben
- falls benötigt setze neue Region mit neuen lokalen Minimum =

- falls zwei Seen/Regionen zusammenfallen/sich berühren => setze Damm
bis alle Pixel das momentan Level erreicht haben
5. speichere Bild
Lineare Operationen?
Beseitigung oder Verbesserung fehlerhafter oder unnötiger Funktionswerte des Musters mit linearen Transformationen.
- Glättung des Bildes (Rauschen entfernen z.B. Röntgenaufnahmen) => Gaußfilter, Mittelwertfilter, ...
- Herausrechnen von Unschärfe / Verwacklung PSF
- Eliminierung von Artefakten
- ....
Was sind die Linearitätseigenschaften?
(Vorverarbeitung)
(Vorverarbeitung)

Spiegelung Y-Achse (lineare Abbildung)
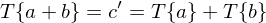
- lineare Transformationen, die durch ein lineares System realisiert werden
- Muster können in verschiedener Weise beeinflusst werden (Erzeugung, Aufnahme, Übetragung, Speicherung, ...)
- durch Anwendung geeigneter Transformationen versucht man u.a. Rauschen zu reduzieren, Wichtige Informationen hervorzuheben (Kontrast verstärken), ideale Muster rekonstruieren (bei Defokussierung), ...
Lineare Systeme:
- f = Funktione (z.B. Bild)
- a = Skalar / Konstante
- T = eine Transformation (z.B. Faltung mit linearen Faltungskern g)
-
 = Kombination mit Konstante
= Kombination mit Konstante -
 = Verknüpfung von zwei Funktionen
= Verknüpfung von zwei Funktionen
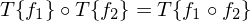
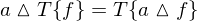
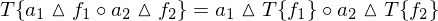
Linearer Filter / Lineare Faltung:
- Behandelt alle Pixel gleich (Impulsantwort ist immer bekannt) Ergebnis ist immer eindeutig .. die Anwendung der Faltungsmaske ist nicht abhängig von Position im Bild
- es gibt eine Umkehrfunktion
- Reihenfolge der Faltungen ist egal (erst Gauß dann Mittelwert = umgekehrt)
- Bsp.:

Was bedeutet Verschiebungsinvarianz (shift-invariance)?
(Vorverarbeitung)
(Vorverarbeitung)
Dies bedeutet, dass die Wirkungsweise eines Operators (z.B. eine Maske eines Mittelwertfilters) nicht von der Position in einem Signal abhängt.
Bei der speziellen Klasse der verschiebungsinvarianten Systeme bewirkt jedoch eine Verschiebung des Einheitsimpulses lediglich
eine entsprechende Verschiebung der Impulsantwort, es ist also
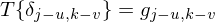
In diesem Fall kann man ohne Einschränkung der Allgemeinheit den Impuls stets an der Stelle u = v = 0 ansetzen und erhält die Impulsantwort des verschiebungsinvarianten Systems zu
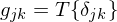
Bei der speziellen Klasse der verschiebungsinvarianten Systeme bewirkt jedoch eine Verschiebung des Einheitsimpulses lediglich
eine entsprechende Verschiebung der Impulsantwort, es ist also
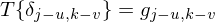
In diesem Fall kann man ohne Einschränkung der Allgemeinheit den Impuls stets an der Stelle u = v = 0 ansetzen und erhält die Impulsantwort des verschiebungsinvarianten Systems zu
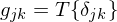
- bei Verschiebung des Systems ändert sich die Impulsantwort nicht
- Bsp.: Mittelwertfilter (Maske = 3x3 = 1) => Impulsantwort immer

- beim Median-Filter oder SNN Filter ändert sich die Impulsantwort bei Verschiebung der Maske (g) bzw. des Systems
Nichtlineare Operationen?
Beseitigung oder Verbesserung fehlerhafter oder unnötiger Funktionswerte des Musters mit nicht-linearen Transformationen.
- Rangordnungsfilter: Kantenerhaltenden Filter ... Kuwahara, SNN, Median, Bilaterale Filter...
- Homomorphe Filter
- morphologische Operationen
- ...
Was sind Homomorphe Systeme bzw. homorphe Filter?
(Vorverarbeitung)
(Vorverarbeitung)
Lineare Systeme (z.B. lineare Filter) sind gut geeignet für die Entfernung von additiven Raushen (gleichverteilt, gleiches Verhältnis) => für nicht-additives z.B. multiplikatives Rauschen nicht geeignet!
Homorphe Systeme sind Generalisierungen von linearen Systemen.
Idee: nicht-additives Signal und Rauschen in additives Reduzieren/Transformieren und dort die lineare Operation ausführen => dann wieder zurücktransformieren.
1. nicht-additiv -> additiv mit Transformation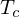 (charakteristisches System)
(charakteristisches System)
2. lineare Transformation (lineare Faltung)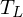
3. wieder zurücktransformieren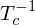
=> nicht-lineare Transformation: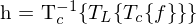
Beispiel 1:
Kombination Signal (signal) und Rauschen (noise) durch Multiplikation (nicht-additives Rauschen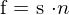 ).
).
Das charkteristische System zur Entfernung des multiplikativen Rauschens:
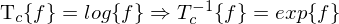
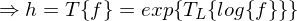
Beispiel 2:
Kombination von Signal und Rauschen durch Konvolution (Faltung)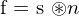 . Durch Fourier-Transformation (FT) kann die Faltung herausgerechnet werden.
. Durch Fourier-Transformation (FT) kann die Faltung herausgerechnet werden.
Das charakteristische System zur Entfernung der Faltung:
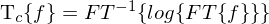
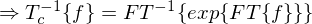
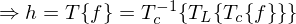
Das Ergebnis von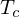 wird Komplexe Ceptrum genannt.
wird Komplexe Ceptrum genannt.
Homorphe Systeme sind Generalisierungen von linearen Systemen.
Idee: nicht-additives Signal und Rauschen in additives Reduzieren/Transformieren und dort die lineare Operation ausführen => dann wieder zurücktransformieren.
1. nicht-additiv -> additiv mit Transformation
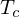 (charakteristisches System)
(charakteristisches System) 2. lineare Transformation (lineare Faltung)
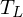
3. wieder zurücktransformieren
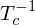
=> nicht-lineare Transformation:
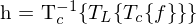
Beispiel 1:
Kombination Signal (signal) und Rauschen (noise) durch Multiplikation (nicht-additives Rauschen
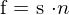 ).
).Das charkteristische System zur Entfernung des multiplikativen Rauschens:
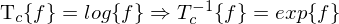
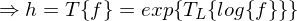
Beispiel 2:
Kombination von Signal und Rauschen durch Konvolution (Faltung)
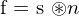 . Durch Fourier-Transformation (FT) kann die Faltung herausgerechnet werden.
. Durch Fourier-Transformation (FT) kann die Faltung herausgerechnet werden.Das charakteristische System zur Entfernung der Faltung:
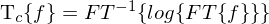
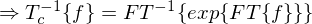
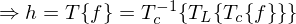
Das Ergebnis von
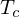 wird Komplexe Ceptrum genannt.
wird Komplexe Ceptrum genannt. Normierungsmaßnahmen?
Angleichung der Werte einiger Parameter an Normalwerte oder bestimmten Wertebereich (z.B. zur besseren Vergleichbarkeit). Die Normierung soll den Wertebreich von Parametern, die für die Klassifizierung irrelevant sind, reduzieren, um bei gegebenen Aufwand für die Klassifikation eine geringe Fehlerwahrscheinlichkeit zu erreichen.
Parameter, die beispielsweise für eine Normalisierung in Frage kommen:
Parameter, die für die Klassen wichtig sind (Unterscheidungsmerkmale), sollten nicht normalisiert werden.
Parameter, die beispielsweise für eine Normalisierung in Frage kommen:
- Größe
- Rotation
- Helligkeit
- Sättigung
- Beleuchtung
Parameter, die für die Klassen wichtig sind (Unterscheidungsmerkmale), sollten nicht normalisiert werden.
Welche Parameter eignen sich zur Normalisierung? Welches Ziel verfolgt die Normalisierung?
(Vorverarbeitung, Normierung)
(Vorverarbeitung, Normierung)
Ziel: Normalisierung dient dem Zweck für Klassen irrelevante Parameter auf normale / vergleichbare Werte zu bringen.
=> Schwankungen in Mustern reduzieren, die keinen Einfluss auf die Bedeutung haben.

Alle A's haben die gleiche Bedeutung unterliegen allerdings Schwankungen (Rotation,Strichstärke, Größe, ...) die zur einfacheren Klassifikation normiert werden sollten.
Parameter, die normalisiert werden:
Parameter, die für eine Klasse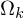 wichtig sind dürfen nicht normalisiert werden!
wichtig sind dürfen nicht normalisiert werden!
Beispiel 1 (Rotation):
- Rotation bei 6 und 9 ist wichtig => nicht normalisieren!
- bei Chromosonen nicht => normieren!
Beispiel 2 (Größe):
- Größe von a und a ist irrelevant => normieren!
- Größe von ´ und / ist relevant => nicht normieren!
=> Schwankungen in Mustern reduzieren, die keinen Einfluss auf die Bedeutung haben.

Alle A's haben die gleiche Bedeutung unterliegen allerdings Schwankungen (Rotation,Strichstärke, Größe, ...) die zur einfacheren Klassifikation normiert werden sollten.
Parameter, die normalisiert werden:
- Größe
- Laufzeit
- Pose (Kombination von Position und Orientierung)
- Rotation
- Energie (Helligkeit)
- Strichstärke (z.B. bei Schriftzeichen)
- Beleuchtung
- charakteristische Sprache (Lautstärke, Akzente, ...)
- Sättigung ...
Parameter, die für eine Klasse
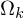 wichtig sind dürfen nicht normalisiert werden!
wichtig sind dürfen nicht normalisiert werden!Beispiel 1 (Rotation):
- Rotation bei 6 und 9 ist wichtig => nicht normalisieren!
- bei Chromosonen nicht => normieren!
Beispiel 2 (Größe):
- Größe von a und a ist irrelevant => normieren!
- Größe von ´ und / ist relevant => nicht normieren!
Wie kann man die Größe normalisieren?
(Vorverarbeitung, Normierung)
(Vorverarbeitung, Normierung)
- lineare Abbildung der Intervalle zu einem normierten Intervall von fester Größe
=> normierung der Größe und Position/Pose
1. durch Resampling (nochmaliges Abtasten in größeren Abständen) => verkleinern
2. durch (bi-)lineare Interpolation zwischen Abtastwerten => vergrößern

Problem: bei Vergrößerung eines Bildes müssen neue Pixel zwischen bestehenden gebildet werden, die den Charakter des Bildes erhalten.
=> normierung der Größe und Position/Pose
1. durch Resampling (nochmaliges Abtasten in größeren Abständen) => verkleinern
2. durch (bi-)lineare Interpolation zwischen Abtastwerten => vergrößern

Problem: bei Vergrößerung eines Bildes müssen neue Pixel zwischen bestehenden gebildet werden, die den Charakter des Bildes erhalten.
Wie kann man die Lage von Mustern normieren?
(Vorverarbeitung, Normierung)
(Vorverarbeitung, Normierung)
Mit Hilfe der Momente:

1. Translation in Schwerpunkt / bzw. des Schwepunktes (Momente)
2. Normalisieren der Größe, Skalierung der Größe auf 1 (durch zentrierte Momente im Bezug zum Schwerpunkt)
3. Rotation auf Hauptachsen / Hauptträgheitsachse (durch zentrierte Momente im Bezug zum Schwerpunkt)
4. Spiegelung an Y-Achse (falls notwendig)
- Musterschwerpunkt berechnen und in Ursprung verschieben
- Muster in Normorientierung bringen

1. Translation in Schwerpunkt / bzw. des Schwepunktes (Momente)
2. Normalisieren der Größe, Skalierung der Größe auf 1 (durch zentrierte Momente im Bezug zum Schwerpunkt)
3. Rotation auf Hauptachsen / Hauptträgheitsachse (durch zentrierte Momente im Bezug zum Schwerpunkt)
4. Spiegelung an Y-Achse (falls notwendig)
Was sind Merkmale? Welche Anforderungen gibt es?
(Merkmale)
(Merkmale)
- Klassifikation bedeutet grob: Muster (fx) => Zahl (Klasse) k
- in Praxis nicht in einem Schritt => Klassifikation wird in mehrere Unterziele zerlegt => Teilschritt löst Teilproblem
- Trennung zwischen Merkmalgewinnung und Vorverarbeitung kann unscharf sein
- Merkmale dienen dazu die Datenmenge zu reduzieren (auf wichtige Aspekte im Muster, Bsp.: nur Tumor nicht ganzer Körper)
- => trennscharfe Informationen herausarbeiten (Bsp.: Unterscheidung O und Q (rechter unterer Teil wichtig!)
- Konzentration auf die für die Klassifikation wichtige Information
Anforderungen an Merkmale:
1. Gütekriterium vorhanden (wie gut ist das Merkmal? => Fehlerwahrscheinlichkeit)
2. Merkmalsgewinnung weitesgehend unabhängig von Vorverarbeitungsoperationen
=> jedes Muster erhält einen Merkmalsvektor
 (das Muster wird durch Transformationen umgeformt in einzelne Zahlenkodierungen (Feature-Vektoren))
(das Muster wird durch Transformationen umgeformt in einzelne Zahlenkodierungen (Feature-Vektoren))Dabei gibt es zwei verschiedene Ansätze:
1. heuristische Methoden (Merkmale aufgrund Intuition, Erfahrungen, ...)
2. analytische Methoden (optimale Merkmale systematisch ableiten, Problemabhängige Reihenentwicklung)
=> Bewertung der Merkmale und Auswahl möglichst guter Untermengen (z.B. über PCA)
Was bedeutet die Berechnung der Merkmale?
- Reduktion der Datenmenge (auf wesentliche/gesuchte Informationen)
- quantitative Analyse der Muster / Bilddaten
- charakteristische Eigenschaften werden durch Merkmale komprimiert dargestellt
- Haralick-Features (Kookurenzen)
- Momente
- statistische Werte
- Fourier-Deskriptoren
- Orthogonale Reihen
- morphologische Eigenschaften
=> Feature-Vektor
Welche Unterschiede gibt es bei der Merkmalsgewinnung?
(Merkmale)
(Merkmale)
- Entwicklung nach einem orthogonalen Basensystem (Verwendung von Koeffizienten eine Reihenentwicklung)
- Merkmale für Texturerkennung
- Merkmale für Objekterkennung
- Merkmale für Spracherkennung
=> Merkmalsbewertung möglich über PCA
Was sind Momente? Wie sind sie definiert und welche Eigenschaften haben sie? Wofür werden sie verwendet?
(Merkmale, Normierung)
(Merkmale, Normierung)
- Momente zählen zu den heuristischen Methoden der Merkmalsgewinnung
- sind gewichtete Mittelwerte aus Helligkeitswerten/Positionen(Binärbild) der Pixel
Sie beschreiben z.B. Formeigenschaften einer binären Region:
-
 Fläche einer Region (oder Summe aller Grauwerte)
Fläche einer Region (oder Summe aller Grauwerte) -
 Schwerpunkt einer Region (oder Mittelwert aller Grauwerte)
Schwerpunkt einer Region (oder Mittelwert aller Grauwerte) - Normalisierung der Skalierung durch normalisierte zentrale Momente
- Orientierung (Richtung der Hauptachse, geringste Trägheit) => Normierung der Orientierung
- Exzentrität (Ausdehnung)
Eigenschaften (normierte zentrale Momente)
- invariant bzgl. Translation
- invariant bzgl. Rotation
- invariant bzgl. Skalierung
invariante Momente "Hu's Momente" => Kombination einfacher Merkmale (Momente)
Wie kann man ein I von einem T unterscheiden ... welche Merkmale wären da sinnvoll?
1. zunächst Beleuchtung und Helligkeit (Energie) normalisieren
2. Schwellwertoperation (Maximierung-Entropie, Approximation von zwei Normalverteilungen, Otsu) => Vordergrund (Muster) Hintergrund trennen
3. Größe (Resampling oder lineare Interpolation) und Lage normieren (mit Momenten)
4. Strichstärke normieren
5. Merkmale bestimmen
2. Schwellwertoperation (Maximierung-Entropie, Approximation von zwei Normalverteilungen, Otsu) => Vordergrund (Muster) Hintergrund trennen
3. Größe (Resampling oder lineare Interpolation) und Lage normieren (mit Momenten)
4. Strichstärke normieren
5. Merkmale bestimmen
- Umfang (Länge äußerer Kontur) T > I
- Fläche T > I
- Rundheit T < I
- Bounding-Box T > I
- Momente (Lage Schwerpunkt) T weiter oben als I
- Momente (Exzentrität) T größer als I
- Anzahl Ecken (HCD) T > I
- Projektion entlang Koordinatenachsen
- Topologische Merkmal z.B. bei 8 und 9 Anzahl der Löcher
Wie funktioniert der Harris-Corner-Detektor (Harris-Punkt-Detektor)?
(Merkmale)
(Merkmale)
- Interessenspunkte => Idee: Ecken (sind in fast jedem Bild enthalten und ihre Position kann eindeutig bestimmt werden)
- robust gegenüber Skalierung, Rotation und Beleuchtung
- kodiert gleichzeitig homogene Bereiche, Kanten und Ecken (Strukturtensor)

Lokale Maxima => Non-Maxima-Unterdrückung
Der Strukturtensor/Autokorrelationsmatrix kodiert lokale Umgebung eines Pixels. Aufgrund der Symmetrie kann er diagonalisiert werden.
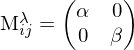
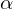 bzw.
bzw. 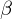 sind die Eigenwerte der Eigenvektoren des Strukturtensors. Sie kodieren die lokale Umgebung.
sind die Eigenwerte der Eigenvektoren des Strukturtensors. Sie kodieren die lokale Umgebung.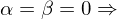 homogene Region
homogene Region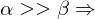 Kante/Kontur
Kante/Kontur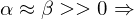 Eckenregion
Eckenregionweitere Details siehe Lernkarte
Orthogonale Reihententwicklung (Merkmale)
Entwicklung des Musters f(x) nach einem orthonormalen Funktionssystem.
Eine Menge von Vektoren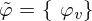 spannt einen Vektorraum V auf, wenn sich jedes Element aus V als Linearkombination von Vektoren aus
spannt einen Vektorraum V auf, wenn sich jedes Element aus V als Linearkombination von Vektoren aus 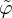 darstellen lässt. Die Koeffizienten c der Linearkombination sind die Entwicklungskoeffizienten.
darstellen lässt. Die Koeffizienten c der Linearkombination sind die Entwicklungskoeffizienten.
Wenn zu jedem Element aus V eindeutige Entwicklungskoeffizienten gehören, so bildet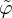
eine Basis für V .
Der Vektor f enthält die Abtastwerte des Musters.
Die Entwicklung eines Vektors f nach orthonormalen Basisvektoren aus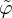 ergibt die eindeutigen Entwicklungskoeffizienten c wenn man die orthonormalen Basisvektoren
ergibt die eindeutigen Entwicklungskoeffizienten c wenn man die orthonormalen Basisvektoren 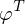 den Zeilen der Matrix
den Zeilen der Matrix 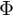 zuordnet. So kann man den Vektor c als Feature-Vektor verstehen, der das Muster eindeutig beschreibt.
zuordnet. So kann man den Vektor c als Feature-Vektor verstehen, der das Muster eindeutig beschreibt.

Die Vektoren f und c haben M und n Kompo-
nenten, M ≥ n, sodass die Matrix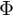 die Größe nM hat. n gibt dabei die Anzahl der verwendeten Basisvektoren an.
die Größe nM hat. n gibt dabei die Anzahl der verwendeten Basisvektoren an.
Dabei ist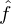 eine Approximation für f , und für n = M ist
eine Approximation für f , und für n = M ist 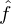 = f , wenn die Basisvektoren vollständig sind.
= f , wenn die Basisvektoren vollständig sind.
In der Praxis reduziert man die Anzahl der Basisvektoren auf die wichtigsten um die Informationen auf einen niedrigdimensionalen Feature-Vektor zu reduzieren. Dabei entsteht ein Fehler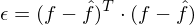 , der aufgrund des Orthogonalitätsprinzips minimal ist.
, der aufgrund des Orthogonalitätsprinzips minimal ist.
Die Entwicklungskoeffizienten c sind nichts anderes als die Beträge der Projektionen der einzelnen Werte aus f auf die Basisvektoren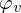 (siehe Orthogonalitätsprinzip).
(siehe Orthogonalitätsprinzip).
Eine Menge von Vektoren
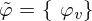 spannt einen Vektorraum V auf, wenn sich jedes Element aus V als Linearkombination von Vektoren aus
spannt einen Vektorraum V auf, wenn sich jedes Element aus V als Linearkombination von Vektoren aus 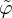 darstellen lässt. Die Koeffizienten c der Linearkombination sind die Entwicklungskoeffizienten.
darstellen lässt. Die Koeffizienten c der Linearkombination sind die Entwicklungskoeffizienten.Wenn zu jedem Element aus V eindeutige Entwicklungskoeffizienten gehören, so bildet
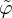
eine Basis für V .
Der Vektor f enthält die Abtastwerte des Musters.
Die Entwicklung eines Vektors f nach orthonormalen Basisvektoren aus
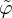 ergibt die eindeutigen Entwicklungskoeffizienten c wenn man die orthonormalen Basisvektoren
ergibt die eindeutigen Entwicklungskoeffizienten c wenn man die orthonormalen Basisvektoren 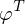 den Zeilen der Matrix
den Zeilen der Matrix 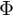 zuordnet. So kann man den Vektor c als Feature-Vektor verstehen, der das Muster eindeutig beschreibt.
zuordnet. So kann man den Vektor c als Feature-Vektor verstehen, der das Muster eindeutig beschreibt.
Die Vektoren f und c haben M und n Kompo-
nenten, M ≥ n, sodass die Matrix
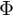 die Größe nM hat. n gibt dabei die Anzahl der verwendeten Basisvektoren an.
die Größe nM hat. n gibt dabei die Anzahl der verwendeten Basisvektoren an. Dabei ist
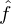 eine Approximation für f , und für n = M ist
eine Approximation für f , und für n = M ist 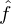 = f , wenn die Basisvektoren vollständig sind.
= f , wenn die Basisvektoren vollständig sind.In der Praxis reduziert man die Anzahl der Basisvektoren auf die wichtigsten um die Informationen auf einen niedrigdimensionalen Feature-Vektor zu reduzieren. Dabei entsteht ein Fehler
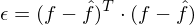 , der aufgrund des Orthogonalitätsprinzips minimal ist.
, der aufgrund des Orthogonalitätsprinzips minimal ist. Die Entwicklungskoeffizienten c sind nichts anderes als die Beträge der Projektionen der einzelnen Werte aus f auf die Basisvektoren
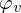 (siehe Orthogonalitätsprinzip).
(siehe Orthogonalitätsprinzip).Orthogonalitätsprinzip (Merkmale)

Dadurch erreicht man durch das "wegwerfen" der Dimensionen (Verwendung weniger Basisvektoren n<<M) einen vertretbaren Fehler
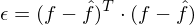 .
.Die Forderung nach Minimierung des Fehlers besagt dann, dass der Abstand zwischen
 und
und 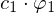
minimal sein soll. Das ist dann der Fall, wenn der Vektor
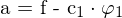
senkrecht auf
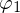 steht, also wenn das Skalarprodukt
steht, also wenn das Skalarprodukt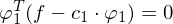
ist.
Das lässt sich auf die Matrix
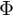 übertragen:
übertragen: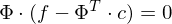
=>
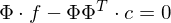
=>
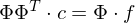
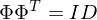
=>
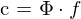
Welche Orthogonalen Basensysteme zur Reihenentwicklung kennen Sie?
(Merkmale)
(Merkmale)
Man kann nun verschiedene "Standardsysteme" die je nachdem in anderen Räumen mit eigenen verschiedenen Basisfunktionen/Basisvektoren verwenden, die bestimmte Sachen besser kodieren oder schlechter. Bei den Basensystemen handelt es sich um heuristiken, die sich als erfolgreich im Bezug zur Feature-Gewinnung und Klassifikationen erwiesen haben.
"Eine Heuristik ist gut, wenn sie erfolgreich ist!"
"Eine Heuristik ist gut, wenn sie erfolgreich ist!"
- Diskrete Fourier-Transformation (DFT)
- Walsh-Transformation
- Diskrete Cosinus-Transformation (DCT)
- Legendre-Polynome
- Hermite-Funktionen
- ....
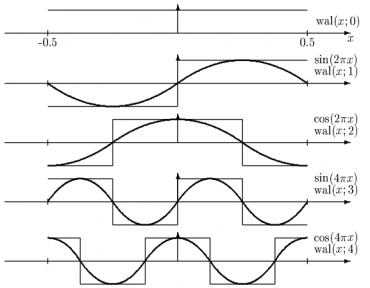
Was ist die Walsh-Hadamard-Transformation ... wie erhält man die Basisvektoren?
(Merkmale)
(Merkmale)
Die Basisvektoren 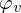 erhält man aus den Walsh-Funktionen in dem man das Intervall (-0.5,+0.5) mit
erhält man aus den Walsh-Funktionen in dem man das Intervall (-0.5,+0.5) mit 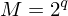 Werten abtasten, wobei es nur Abtastwerte +/- 1 (Amplitude) gibt. Die Transformationsmatrix
Werten abtasten, wobei es nur Abtastwerte +/- 1 (Amplitude) gibt. Die Transformationsmatrix 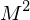 lässt sich rekursiv aus der HADAMARD-Matrix mittels Kronecker-Produkt
lässt sich rekursiv aus der HADAMARD-Matrix mittels Kronecker-Produkt 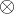 berechnen.
berechnen.

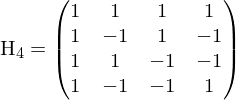
Diese Matrix enthält die Abtastwerte der ersten vier Walsh-Funktionen und bildet ein orthogonales Basensystem (alle Zeilen und Spalten orthogonal, nur 1 und -1 als Koeffizienten).
Die Hadamard-geordnete Walsh-Hadamard-Transformation (WHT) eines Mustervektors f mit M Komponenten erfolgt gemäß
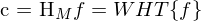
Die Inverse
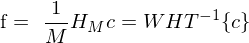
 erhält man aus den Walsh-Funktionen in dem man das Intervall (-0.5,+0.5) mit
erhält man aus den Walsh-Funktionen in dem man das Intervall (-0.5,+0.5) mit 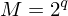 Werten abtasten, wobei es nur Abtastwerte +/- 1 (Amplitude) gibt. Die Transformationsmatrix
Werten abtasten, wobei es nur Abtastwerte +/- 1 (Amplitude) gibt. Die Transformationsmatrix 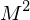 lässt sich rekursiv aus der HADAMARD-Matrix mittels Kronecker-Produkt
lässt sich rekursiv aus der HADAMARD-Matrix mittels Kronecker-Produkt 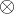 berechnen.
berechnen.
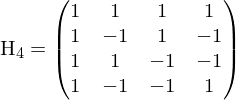
Diese Matrix enthält die Abtastwerte der ersten vier Walsh-Funktionen und bildet ein orthogonales Basensystem (alle Zeilen und Spalten orthogonal, nur 1 und -1 als Koeffizienten).
Die Hadamard-geordnete Walsh-Hadamard-Transformation (WHT) eines Mustervektors f mit M Komponenten erfolgt gemäß
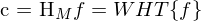
Die Inverse
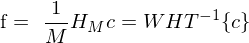
- nur Addition und Subtraktion nötig
- Resultat (c) sind reelle Zahlen
- gibt schnelle Implementierung mittels Faktorisierung
Was ist die Idee der Faktorisierung der WHT?
(Merkmale)
(Merkmale)
- Faktorisierung bedeutet die Zerlegung eines Objektes in mehrere nichttriviale Faktoren die zu dem gleichen Ergebnis führen.
- "Teile und Hersche" => Divide and Conquer
- Kann rekursiv implementiert werden => Fast WHT
- gleichartige Zwischenergebnisse sind auf diese Weise mehrfach wiederverwendbar
- Aufwand von

- die Berechnung endet mit 8
 Matrixberechnungen
Matrixberechnungen

Diskrete Fourier-Transformation als orthogonale Basis ... was passiert da? Was sind die Basisvektoren? Welche eigenschaften hat die DFT?
(Merkmale)
(Merkmale)
- Features (c, die Entwicklungskoeffizienten) sind translationinvariant
- wichtiges Werkzeug für lineare, verschiebungsinvariante Systeme
- ermöglicht Wege die Ausgabe von linearen Systemen zu berrechenen
- kann durch FFT schnell berechnet werden
- erlaubt Visualisierung des Effektes eines linearen Systems
- invariant zur Translation
- einfache Matrixvektor-Operation
- sie bildet komplexe Vektoren auf komplexe Vektoren ab
- die Foruier-Matrix lässt sich aus der n'ten primitiven Einheitswurzel konstruieren wobei M die Länge des Vektors f ist.
- die Basisvektoren

-


Was ist die Idee der Faktorisierung der DFT?
(Merkmale)
(Merkmale)
- Faktorisierung bedeutet die Zerlegung eines Objektes in mehrere nichttriviale Faktoren die zu dem gleichen Ergebnis führen.
- "Teile und Hersche" => Divide and Conquer
- Kann rekursiv implementiert werden => Fast Fourier Transformation
- gleichartige Zwischenergebnisse sind auf diese Weise mehrfach wiederverwendbar
- Berechnung der DFT der Größe 2n zunächst in zwei Berechnungen der Größe n aufteilen
- => Vektoren mit geraden bzw. ungeraden Indizes
- und beide Teilergebnisse nach der Transformation wieder zu einer zusammenzufügen
- => Berechnung DFT halbe Länge nur ein viertel der komplexen Multiplikationen und Additionen und diese Vorschrift mehrfach hintereinander anwendbar ist (rekursives Vorgehen) ...
- ... Aufwand (rekursive Berechnung)

Wie funktioniert Appearence-Based Objectrecognition mittels Eigenspaces?
(Merkmale)
(Merkmale)

Originalbilder und ihre Repräsentation im Eigenspace (Feature-Vektor
 ).
).Idee (Funktionsweise):
- Darstellung des Bildes
 als Spaltenvektor
als Spaltenvektor  in dem das Bild Zeilenweise eingetragen wird
in dem das Bild Zeilenweise eingetragen wird - Der Vergleich zwischen 2 Bildern
 und
und  mit
mit  reduziert sich auf die Berechnung des Skalarproduktes
reduziert sich auf die Berechnung des Skalarproduktes  . Je größer
. Je größer  desto ähnlicher die beiden Bilder (Projektion des einen Vektor auf den anderen)
desto ähnlicher die beiden Bilder (Projektion des einen Vektor auf den anderen) - Der Bildverktor ist zu groß für schnelle Berechnungen, daher reduziert man mittels einer linearen Transformation auf Featurevektor

- Für alle Eingabevektoren (Eingabebilder, z.B. rotierter Locher) bildet man den Mean-Vektor
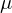 . zieht ihn von jedem Bild ab und schreibtdie Bildvektoren in die Matrix
. zieht ihn von jedem Bild ab und schreibtdie Bildvektoren in die Matrix 
- Man bestimmt dann die Eigenvektoren
 von
von  (z.B. mittels SVD)
(z.B. mittels SVD) - Man kann dann aus Linearkombination aus
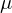 und
und  Eigenvektoren den Feature-Vektor
Eigenvektoren den Feature-Vektor  im Eigenspace berechnen
im Eigenspace berechnen 
Praktische Anwendung zur Objekterkennung:
- Für jede Klasse
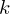 werden
werden  Feature-Vektoren im Eigenspace generiert (für jedes verwendete Bild unter verschiedenen Aufnahmebedingungen => Trainingsset) und entsprechend
Feature-Vektoren im Eigenspace generiert (für jedes verwendete Bild unter verschiedenen Aufnahmebedingungen => Trainingsset) und entsprechend 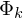 (enthält verwendete Eigenvektoren aus K)
(enthält verwendete Eigenvektoren aus K) - die Vektoren
 einer Klasse
einer Klasse 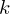 bildern das Modell
bildern das Modell 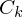
- die Korrelation zwischen zwei Bildern lässt sich dann approximiert durch die Eukldische Distanz aus
 berechnen
berechnen - ist wesentlich schneller, da
 wesentlich weniger Dimensionen hat
wesentlich weniger Dimensionen hat
Klassifikation mittels Eigenspaces:
Die Klassifikation eines Bildvektors
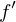 (Voraussetzung: Bild befindet sich in Trainingsset) verläuft unter Verwendung des Modells
(Voraussetzung: Bild befindet sich in Trainingsset) verläuft unter Verwendung des Modells 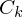 und der Eigenwertmatrix
und der Eigenwertmatrix 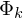
1. Transformation des Bildvektors
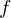 in den Eigenspace =>
in den Eigenspace => 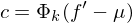
2. Vergleich mit allen Eigenspace-Vektoren aus
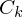
3. Wähle Vektor mit minimaler Distanz zu
 => Objekt gefunden!
=> Objekt gefunden!Was ist ein Klassifikator? Welche kennen Sie?
(Klassifikation)
(Klassifikation)
Klassifikatoren werden für das überwachte Lernen verwendet.
1. Auswahl Klassen (z.B. durch Markierung bestimmter Gewebsbereiche im Bild => Tumor, kein Tumor, Stroma, Entzündung, ...)
2. Zuweisung aller Pixel zu den entsprechenden Klassen -> verschiedene Methoden / Klassifikatoren

Eine lineare Funktion teilt den Merkmalsraum (2D) in zwei Klassen auf. Anhand des trainierten Klassifikators wird im Klassifikationsschritt das Muster anhand seiner Merkmalsausprägungen unmittelbar einem Klasse zugeordnet.
1. Auswahl Klassen (z.B. durch Markierung bestimmter Gewebsbereiche im Bild => Tumor, kein Tumor, Stroma, Entzündung, ...)
2. Zuweisung aller Pixel zu den entsprechenden Klassen -> verschiedene Methoden / Klassifikatoren
- Maximum-Likelihood ( Zuweisung anhand der größten Zugehörigkeitswahrscheinlichkeit)
- Minimum-Distance ( Zuweisung anhand des nächstgelegenen Klassenmittelpunktes)
- K-Nearest-Neighbours
- Support Vector Machine
- Neuronale Netze (iterative Optimierung der Verbindung zwischen den einzelnen Einheiten (Pixeln)
- ...
- ein Klassifikator dient dazu eine Funktion zu finden, die die Merkmale möglichst optimal in Klassen einteilt (aufgrund von ausgewählten Stichproben)
- der trainierte Klassifikator wird mit dem Ziel eingesetzt, neue, nicht in der Stichprobe enthaltene Muster der Klassen
 anhand der Merkmale automatisch zuzuordnen.
anhand der Merkmale automatisch zuzuordnen.

Eine lineare Funktion teilt den Merkmalsraum (2D) in zwei Klassen auf. Anhand des trainierten Klassifikators wird im Klassifikationsschritt das Muster anhand seiner Merkmalsausprägungen unmittelbar einem Klasse zugeordnet.
Was versteht man unter der Fourier-Transformation?

Man kann jede periodische, kontinuierliche Funktion als Summe von Sinus- und Kosinustermen konstruieren (siehe Bild rotes Signal).
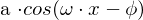
a = Amplitude
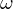 = Frequenz
= Frequenz = Phase
= PhaseDas Fourier-Integral beschreibt die ursprüngliche Funktion g(x) als Summe unendlich vieler Kosinus-/Sinusfunktionen mit kontinuierlichen (positiven) Frequenzwerten, wofür die Funktionen
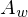 und
und 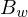 eindeutige Frequenzkoeffizienten liefern. Das Signal g(x) bzw, f(x) ist durch die zugehörigen Funktionen
eindeutige Frequenzkoeffizienten liefern. Das Signal g(x) bzw, f(x) ist durch die zugehörigen Funktionen 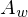 bzw.
bzw. 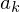 und
und 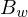 bzw.
bzw. 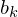 eindeutig definiert. Sie beschreiben die Amplitude und die Frequenz des Signals g(x) bzw. f(x).
eindeutig definiert. Sie beschreiben die Amplitude und die Frequenz des Signals g(x) bzw. f(x).Die Fourier-Transformation hat eine Reihe von Basisfunktionen (bestehend aus Sinus- und Cosinus-Funktionen) .. die sogenannten Fourier-Reihen.
Durch Kombination der Fourier-Reihen mit den eindeutigen Frequenzkoeffizienten wird das Signal g(x) bzw. f(x) im Ortsbereich eindeutig im Frequenzbereich G(w) bzw.
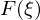 beschrieben.
beschrieben.Welche Eigenschaften hat die Fourier-Transformation?

Symmetrie:
Um den Urpsrung symmetrisch
Linearität:
Die Fourier-Transformation ist eine lineare Operation (w = Frequenz)
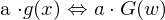
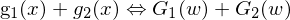
Ähnlichkeit:
Wird die ursprüngliche Funktion g(x) in Zeit oder Raum skaliert, so tritt der entgegengesetzte Effekt im zugehörigen Fourier-Spektrum auf.
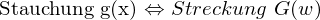
Verschiebungseigenschaft:
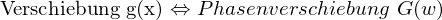
Faltungseigenschaft:
Eine Multiplikation der Funktion in einem Raum (Orts- oder Spektralraum) entspricht einer linearen Faltung (
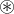 ) der zugehörigen Transformation im jeweils anderen Raum.
) der zugehörigen Transformation im jeweils anderen Raum.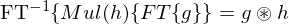
Flashcard set info:
Author: JanBo
Main topic: Digitale Bildverarbeitung
Topic: Mustererkennung
School / Univ.: Universität Koblenz-Landau
City: Koblenz
Published: 13.09.2012
Tags: Paulus
Card tags:
All cards (73)
no tags














 , mit
, mit  und
und  die den Schwerpunkt definieren und als Referenz dienen.
die den Schwerpunkt definieren und als Referenz dienen.



 berechnet und direkt anhand des trainierten Klassifikators (aus den Stichproben) im Merkmalsraum einer Klasse
berechnet und direkt anhand des trainierten Klassifikators (aus den Stichproben) im Merkmalsraum einer Klasse 

