Get these flashcards, study & pass exams. For free! Even on iPhone/Android!

Im Falle eines einzigen gemeinsamen latenten Merkmals,
lautet die formale Darstellung der Faktorenanalyse


Zum Vergleich das Modell der einfachen Regression

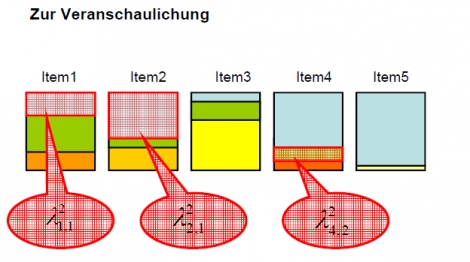
Zur Veranschaulichung

Die Box steht für die Varianz des Items.
Die hellblaue Fläche für den Anteil an Varianz, der durch den ersten Faktor erklärt wird.
Die hellgrünen Flächen für den Anteil an Varianz, der durch den
zweiten Faktor erklärt wird.
Die anderen Farben für die „itemspezifischen“ Einflüsse, die auf das jeweilige Item wirken. Sie sind bei jedem Item anders.

Multiple Faktorenanalyse - Korrelation zwischen Items


Die Berechnung kann sinnvoll sein um die Korrelation zu überprüfen wie es theoretisch ist (diese Berechnung) und realen Ergebnissen. Dies kann dabei helfen um zu überprüfen ob es möglicherweise noch einen weiteren, nicht entdeckten, Faktor gibt  - wenn die theoretischen und realen Ergebnisse nicht übereinstimmen.
Um von einer Korrelation zu sprechen sollte der Unterschied nicht größer sein als 0.1

Ladungen der Faktoren pro Item




Ladung (Lambda) - Wichtig: Man liest dies von hinten (Faktor) nach vorne (Item)
-Ladung von Faktor 1 im Item 1
-Ladung von Faktor 1 im Item 2

Die mathematische Herausforderung im Rahmen der Faktorenanalyse ist die Bestimmung der (unbekannten) Ladungen sowie die Festlegung der Faktorenzahl.

Die Grundidee der Parameterschätzung basiert darauf, zunächst jenen Faktor mit dem größten Eigenwert zu „extrahieren“. Dadurch wird die Summe der quadrierten verbleibenden Korrelationen zwischen den Items am stärksten minimiert.

Daraus folgt, dass man die Ladungen des 1. Faktors so bestimmt, dass


Die mathematische Name dieses Problems nennt sich „Eigenwert – Eigenvektor Problem“ und wurde (zum Glück) bereits gelöst.
Der Lösungsweg erfolgt iterativ und ist in realen Situationen für die händische Berechnung viel zu aufwändig.

Nach Extraktion des ersten Faktors (= Schätzung der Ladungen des ersten Faktors), wird der zweite Faktor nach derselben Grundidee extrahiert. Allerdings verwendet man hierfür nicht die originalen Korrelationen, sondern die um den Einfluss des ersten Faktors reduzierten. Diese Korrelationen werden „Restkorrelationen“ genannt.

Im Rahmen der Faktorenanalyse wurden eine Vielzahl an Extraktionsverfahren entwickelt. Die zwei am häufigsten angewandten sind
– die Hauptachsenanalyse („principal axis“) und
– die Hauptkomponentenanalyse („principal components“).

Bei der Hauptkomponentenanalyse wird davon ausgegangen, dass sich die Varianz eines Items vollständig durch die gemeinsamen Faktoren erklären lässt. Demnach sind alle Kommunalitäten (und somit auch die Korrelationen eines Items mit sich selbst) gleich 1. Als Konsequenz werden so viele Faktoren extrahiert, wie es Items gibt.
Sie ist die Standardeinstellung bei Berechnung einer Faktorenanalyse in SPSS.

Bei der Hauptachsenanalyse wird davon ausgegangen, dass sich die Varianz eines Items immer in die Kommunalität und die Einzelrestvarianz aufteilt. Demnach sind die Kommunalitäten (und somit auch die Korrelationen eines Items mit sich selbst) kleiner als 1.
Ziel ist es also, nur die durch die gemeinsamen Faktoren erklärbare Varianz zu beschreiben.
Da zu Beginn der Datenanalyse die Kommunalitäten nicht bekannt sind (=„Kommunalitätenproblem“), werden die Faktoren zunächst mittels Hauptkomponentenanalyse geschätzt und iterativ (=schrittweise) „verbessert“ („Kommunalitäteniteration“).
Kommunalitätenproblem - Vorgehensweise:
- „1“ wird in die Hauptdiagnoale geschrieben (jedes Items mit sich selbst)
- Mit der Lösung erhält man (etwas falsche) Ladungen
- Durch diese Ladungen erhält man (falsche) Kommunalitäten.
- Diese setzt man dann wiederrum in die Hauptdiagonale ein und führt die gesamte Berechnung neu durch.
- Dadurch kommt man zu immer besseren Daten.

Laut Backhaus et al.* unterscheidet sich die Interpretation der Faktoren je nach Methode.
Bei der Hauptkomponentenanalyse geht es darum, die hoch auf einem Faktor ladenden Items zu einem Sammelbegriff zusammenzufassen.
Bei der Hauptachsenanalyse geht es darum, die „Ursachen“ für die (hohen) Korrelationen zwischen den Items zu finden.

Mathematisch sind dies 2 leicht verschiedene Modelle, dies ist aber nicht weiter zu beachten (State of the art – in der Literatur wird immer die Hauptachsenanalyse erklärt – aber bei SPSS mit der Hauptkomponentenanalyse berechnet.

Für die Bestimmung der Anzahl an Faktoren gibt es fünf üblicherweise herangezogene Kriterien

• Faktorenzahl wird a priori festgelegt
• alle Restkorrelationen sind nahe 0 (z.B.: <.2)
• der Eigenwert des zuletzt extrahierten Faktors ist kleiner 1* (auch "Kaiser-Kriterium": im übertragenen Sinn ist damit die „Information, die über den Faktor vorliegt“ geringer als die Information eines einzigen Items),
Ein Item hat die Varianz 1; wenn ein Faktor einen Eigenwert von weniger als 1 hat, dann enthält der Faktor weniger Information als ein einziges Item. Es macht dann keinen Sinn diesen Faktor zu verwenden.
• der Verlauf des Eigenwertediagramms (Screeplot)
Bei der Betrachtung des Eigenwertediagramms, wird jene Stelle gesucht, an der Verlauf das Eigenwertediagramm „abflacht“ (= Elbow Kriterium). Die Faktoren vor dem „Knick“ werden in der weiteren Analyse berücksichtigt.
• die Parallelanalyse
Bei der Parallelanalyse werden zumindest 100 Datensätze von Zufallszahlen erzeugt, wobei die Anzahl an Items und der Stichprobenumfang dem empirisch gewonnenen Datensatz entspricht. All diese Datensätze werden einer Faktorenanalyse unterzogen und die aus jeder Analyse gewonnenen Eigenwerte werden pro Faktor gemittelt. Als relevante nichttriviale Faktoren werden all jene Faktoren bezeichnet, deren Eigenwerte über jenen der (gemittelten) Eigenwerte der Parallelanalyse liegen.Dort wo die Parallelanalyse (zufällige Werte) die realen Eigenwerte schneidet, dort liegt die Grenze. PROBLEM: sehr aufwändig.

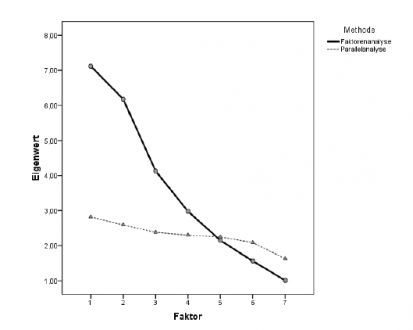
Für die Bestimmung der Faktorenzahl gibt es keine generellen Vorschriften, sodass der Grad an Subjektivität hier relativ hoch ist.

Die Ladungsmatrix bildet die Grundlage für die inhaltliche Interpretation der Faktoren. Hierfür werden üblicherweise die in einem Faktor hoch (=ideal sind Items mit Ladungen über 0.7) und in allen anderen Faktoren niedrig ladenden Items (ideal sind hier Ladungen unter 0.3) herangezogen. Diese Items werden auch als „Marker-Items“ bezeichnet.
Zeichnet man die Items als Punkte in einem Raum mit so vielen Dimensionen wie es Faktoren gibt, so liegen „Marker-Items“ „nahe“ an den Koordinatenachsen.

Vorgehen:
- Man nimmt Items die in einem Faktor hoch laden = Marker-Items
- Diese sollten im Idealfall in anderen Items niedrig laden.
- Bei diesen Items sollte man die Eigenschaft dann gut erkennen.

Wegen der Vorgehensweise bei der Parameterschätzung sind derartig hohe Ladungen bei der „Erstlösung“ in der Praxis aber eher selten.
Aus diesem Grund werden die Faktoren zur besseren Interpretierbarkeit „rotiert“.

Ziel ist eine einfache Struktur („simple structure“) bei der jedes Item nach Möglichkeit nur in einem Faktor hoch in den anderen Faktoren jedoch gering lädt.
Dadurch ergeben sich neue, besser interpretierbare Ladungen.

• Marker-Items für Faktor 1: 2,3,4,6
• Marker-Items für Faktor 2: 1,5 und 7
- Diese liegen in der Grafik nahe der Koordinatenachse F2

Ladungen – man sieht ein rechtwinkeliges Dreieck – wenn die orange Linie mittels der beiden Ladungen berechnet wird, ist das Ergebnis die Kommunalität (Ursprung zu Item). = Notwendig für Faktorenrotation.

Die Items liegen nicht auf den Achsen - Faktorenrotation
Ziel: Man dreht die Achsen, damit die Achsen auf den Items liegen– jedoch darf sich die Entfernung vom Mittelpunkt zu den Items (= Kommunalität) nicht ändern.

Wegen der Vorgehensweise bei der Parameterschätzung sind derartig hohe Ladungen bei der „Erstlösung“ in der Praxis aber eher selten.
Aus diesem Grund werden die Faktoren zur besseren Interpretierbarkeit „rotiert“.

Ziel ist eine einfache Struktur („simple structure“) bei der jedes Item nach Möglichkeit nur in einem Faktor hoch in den anderen Faktoren jedoch gering lädt.
Dadurch ergeben sich neue, besser interpretierbare Ladungen.

Durch die Rotation ändern sich

• die Ladungen,
• die Eigenwerte und
• möglicherweise auch die Interpretation der Faktoren.

Unverändert bleiben

• die Kommunalitäten und
• der Anteil der durch die Faktoren erklärbaren Varianz.

Wird der rechte Winkel zwischen den Faktorenachsen beibehalten (= unabhängige Faktoren) spricht man von einer orthogonalen Rotation.

Gibt man die Forderung nach unabhängigen Faktoren auf (=Faktorenachsen müssen nicht im rechten Winkel aufeinander stehen) so spricht man von schiefwinkeligen (= oblique) Rotationen.

Die bekannteste Art der Faktorenrotation ist die „Varimax-Rotation“. Hierbei werden die Faktoren so rotiert, dass die Varianz der Ladungen innerhalb eines Faktors maximal wird. Das bedeutet, das Ziel ist pro Faktor sowohl hohe als auch niedrige Ladungen zu haben, um so die Faktoren leichter benennen zu können.

Rechtwinkelig bedeutet unabhängig. Wenn man schiefwinkelige Faktorenlösungen nimmt, dann sind die Faktoren miteinander korreliert.

Da es das Ziel der Faktorenanalyse ist, die Zahl der Kennwerte zu reduzieren (aus vielen Items sollen deutlich weniger Faktoren resultieren), ist es nötig, Kennwerte für die Ausprägungen der Personen in den zu Grunde liegenden Faktoren zu ermitteln. Diese Kennwerte nennen sich Faktorwerte (auch „Skalenwerte“ genannt).

Man unterscheidet zwischen gewichteten und ungewichteten Faktorwerten.

Ungewichtete Faktorwerte
Die Berechnung der ungewichteten Faktorwerte erfolgt pro Person z.B. durch aufsummieren oder mitteln der Punkte jener Items, die in einem Faktor hoch laden.
Items, die in mehreren Faktoren ähnlich hohe Ladungen aufweisen, werden entweder jenem Faktor zugerechnet, in dem sie die höchste Ladung aufweisen oder bei der Berechnung der Faktorwerte nicht berücksichtigt.
Ist die Ladung eines Items in einem Faktor negativ, so muss das Item „umgepolt“ werden.

Gewichtete Faktorwerte
Da bei der ungewichteten Berechnung der Faktorwerte die unterschiedliche Konstruktvalidität der Items nicht berücksichtigt wird und Items, die in zwei oder mehr Faktoren ähnlich hohe Ladungen haben, problematisch sind, werden die Items je nach Ladung eines Items in einem Faktor gewichtet.

• Das Umpolen der Items ist hierbei nicht nötig.
• Es resultieren pro Faktor standardisierte Faktorwerte.
• Für die Berechnung stehen in SPSS unterschiedliche Methoden zu Verfügung.

Aufgrund der negativen Ladung von Item 5 in Faktor 1 muss dieses Item für die Berechnung des ungewichteten Faktorwerts (und auch für die Berechnung der Reliabilität) „umgepolt“ werden.

Es lassen sich zwei Arten von Faktorenanalysen unterscheiden

• die explorative und
• die konfirmatorische Faktorenanalyse.

Explorative Faktorenanalysen
Die explorative Faktorenanalyse wird verwendet, wenn noch keine Hypothesen über die Anzahl an Faktoren und die Zuordnung der Items zu den Faktoren existieren.
Die Zahl der Faktoren und die Zuordnung der Items zu den Faktoren wird mittels der zuvor besprochenen Vorgehensweisen bestimmt.

Konfirmatorische Faktorenanalysen
Bei der konfirmatorischen Faktorenanalyse sollen eine oder mehrere zuvor theoretisch festgelegte Faktorenstrukturen anhand empirischer Daten auf ihre Gültigkeit hin überprüft werden. Demnach müssen die Faktorenzahl und die Zuordnung der Items zu den Faktoren bekannt sein.

Die konfirmatorische Faktorenanalyse zählt zu den Strukturgleichungsmodellen (SEM) in deren Rahmen geprüft wird, wie gut ein oder mehrere theoretisch formulierte Modelle, die erhobenen Daten beschreiben. Für diese Fragestellung werden sowohl Signifikanztests als auch Indices zur Überprüfung der Modellanpassung an die Daten verwendet.

Die Faktorenanalyse trifft keine Aussagen über die Dimensionalität der Items.

Die klassische Variante der Faktorenanalyse beruht auf der Berechnung von Pearson Korrelationen bzw. Kovarianzen.
Demnach sollten die für eine Faktorenanalyse herangezogenen Items metrisch sein.

Weiters sind die Ergebnisse (vor allem die Anzahl an Faktoren) stark stichprobenabhängig.
Je homogener die Stichprobe, desto geringer die Korrelationen zwischen den Items und umso mehr Faktoren ergeben sich. Demnach müssten z.B. die Gewichtungen für die gewichteten Summen in jeder Stichprobe neu berechnet werden.

Für den Fall dichotomer Items sollte als Basis für die faktorenanalytischen Berechnungen die tetrachorische Korrelation herangezogen werden. Die Höhe der Vierfelderkorrelation (=Pearson Korrelation für zwei dichotome Items) hängt stark von den Itemschwierigkeiten der Items ab und führt somit zu artifiziellen Ergebnissen. Die Faktoren bilden zumeist Gruppen von in etwa gleich schweren Items.

Mitunter bilden die Faktoren nur das Antwortwortverhalten der Personen ab. So können z.B. Fragen, die von Personen meist bejaht werden, in einem gemeinsamen Faktor hoch laden auch wenn damit inhaltlich völlig unterschiedliche „Dimensionen“ abgefragt wurden.

Kommunalitäten der Items, h²i

Wie viel der Varianz im Item i kann durch die extrahierten Faktoren erklärt werden?
h²i ≤ rel(Xi)

Eigenwerte der Faktoren, Eig(Fj)

• Wie viel der Gesamtvarianz der Items kann durch den Faktor erklärt werden?
• Mögliche Höhe der Eigenwerte ist abhängig von der Anzahl der Items!!

Eig(F1) = 0.10² + 0.43² + 0.66² + 0.89² + 0.82² = 2.095
Eig(F2) = 0.88² + 0.55² + (-0.23)² + 0.12² + 0.10² = 1.15