Was sind die Kennzeichen eines psychologischen Tests?
Definition eines (psychologischen) Tests (Moosbrugger & Kelava, 2008, S. 2):
Ein Test ist ein wissenschaftliches Routineverfahren zur Erfassung eines oder mehrerer empirisch abgrenzbarer psychologischer Merkmale mit dem Ziel einer möglichst genauen quantitativen Aussage über den Grad der individuellen Merkmalsausprägung.
Ein Test ist ein wissenschaftliches Routineverfahren zur Erfassung eines oder mehrerer empirisch abgrenzbarer psychologischer Merkmale mit dem Ziel einer möglichst genauen quantitativen Aussage über den Grad der individuellen Merkmalsausprägung.
- Muss wissenschaftlich sein
- Soll ein Routineverfahren sein
- Soll psychologische Merkmale messen
- Soll eine quantitative Aussage machen (soll eine Messung liefern)
Tags: Definition, Merkmal, Routineverfahren, Test, Wissenschaft
Quelle: F3
Quelle: F3
Was kennzeichnet Wissenschaftlichkeit bzw. wann kann man von wissenschaftlich sprechen?
Was sind die primären Aufgabengebiete der Testtheorie?
Was sind die primären Aufgabengebiete der Testtheorie?
Um von wissenschaftlich sprechen zu können, muss es eine Theorie darüber geben, unter welchen Bedingungen welche Aussagen anhand der Testergebnisse ableitbar sind.
Demnach sollte eine möglichst genaue Vorstellung über das zu messende Merkmal vorliegen und der Test testtheoretischen Qualitätsansprüchen entsprechen.
Die (primären) Aufgabengebiete der Testtheorie sind
Demnach sollte eine möglichst genaue Vorstellung über das zu messende Merkmal vorliegen und der Test testtheoretischen Qualitätsansprüchen entsprechen.
Die (primären) Aufgabengebiete der Testtheorie sind
- die Formulierung des theoretischen Hintergrunds über die Verbindung von zu messendem Merkmal und im Test gezeigtem Verhalten sowie
- die Festlegung und Quantifizierung notweniger Qualitätsansprüche.
Tags: Definition, Testtheorie, Wissenschaft
Quelle: F4
Quelle: F4
Wann spricht man von einem Routineverfahren?
Von einem Routineverfahren spricht man, wenn Durchführung und Auswertung
(Wird häufiger angewandt: es gibt Erfahrungswerte und ist an größeren Stichproben erprobt und Wissen über Durchführung und Auswertung soll vorhanden sein)
- bereits an einer größeren Stichprobe erprobt sind und
- so detailliert beschrieben sind, dass das Verfahren auch von anderen „TestleiterInnen“ bei anderen Personen einsetzbar ist.
(Wird häufiger angewandt: es gibt Erfahrungswerte und ist an größeren Stichproben erprobt und Wissen über Durchführung und Auswertung soll vorhanden sein)
Tags: Definition, Routineverfahren, Tests
Quelle: F5
Quelle: F5
Was versteht man unter einem psychologischen Merkmal?
Bei einem psychologischen Merkmal handelt es sich um einen Oberbegriff für
Diese meist nicht direkt beobachtbaren (=latenten) Merkmale sollen mit Hilfe von messbaren Sachverhalten „erschlossen“ werden.

(Es werden Items gemessen und auf Merkmale geschlossen)
- relativ stabile und konsistente Merkmale (auch „Eigenschaften“ oder „Traits“ genannt),
- zeitlich begrenzte biologische, emotionale und kognitive Zustände sowie (auch „States“ genannt) und
- Erlebens- und Verhaltensweisen.
Diese meist nicht direkt beobachtbaren (=latenten) Merkmale sollen mit Hilfe von messbaren Sachverhalten „erschlossen“ werden.

(Es werden Items gemessen und auf Merkmale geschlossen)
Tags: Definition, Merkmal
Quelle: F6
Quelle: F6
Was versteht man darunter das Tests quantitative Aussagen machen sollen?
Ziel psychologischer Tests ist es die Ausprägung des Merkmals der gestestete Person zu messen.
Messen bedeutet einem Objekt (empirisches Relativ) einen Zahlenwert (numerisches Relativ) so zuzuordnen, dass zumindest eine Eigenschaft des numerischen Relativs auch für das empirische Relativ gilt.
(vgl. Bortz J. (1999) Statistik für Sozialwissenschaftler, 5. Auflage S. 18 - 20).
Dieser Zahlenwert kann in weiterer Folge dazu verwendet werden, die Person mit anderen Personen vergleichen oder einer Personengruppe zuordnen zu können.
Je nach theoretischer Fundierung des Messvorgangs haben die erzielten Zahlenwerte unterschiedliches Skalenniveau.


Messen bedeutet einem Objekt (empirisches Relativ) einen Zahlenwert (numerisches Relativ) so zuzuordnen, dass zumindest eine Eigenschaft des numerischen Relativs auch für das empirische Relativ gilt.
(vgl. Bortz J. (1999) Statistik für Sozialwissenschaftler, 5. Auflage S. 18 - 20).
Dieser Zahlenwert kann in weiterer Folge dazu verwendet werden, die Person mit anderen Personen vergleichen oder einer Personengruppe zuordnen zu können.
Je nach theoretischer Fundierung des Messvorgangs haben die erzielten Zahlenwerte unterschiedliches Skalenniveau.


Tags: Definition, Messung, Skalenniveau, Test
Quelle: F8
Quelle: F8
Was versteht man unter einem Fragebogen?
Der Begriff wird im Deutschen für Unterschiedliches verwendet.
Gemeinsam ist beiden, dass das „Erfragen“ im Vordergrund steht.
- schriftliche Befragungen zur Erhebung von - demoskopischen Daten- schulischen Daten- medizinischen Daten- usw.
- Instrument zur „Selbst- oder Fremdeinschätzung“ - wird meist zur Erfassung von Persönlichkeitseigenschaften und Interessen verwendet- Häufig auch als Persönlichkeits“test“ bezeichnet
Gemeinsam ist beiden, dass das „Erfragen“ im Vordergrund steht.
Tags: Definition, Fragebogen
Quelle: F11
Quelle: F11
Welche Testarten können unterschieden werden?
Je nach Merkmal, das erfasst werden soll, werden drei/vier unterschiedliche Testarten unterschieden
* Die Bezeichnung „Persönlichkeitsfragebogen“ unterscheidet sich bewusst von der im Buch von Moosbrugger & Kelava (2008), S.29 gewählten, da die Personen hier „befragt“ werden.
- Leistungstests
- Persönlichkeits- und Interessensfragebögen*
- [objektive Persönlichkeitstests]
- projektive Verfahren
- apperative Tests
* Die Bezeichnung „Persönlichkeitsfragebogen“ unterscheidet sich bewusst von der im Buch von Moosbrugger & Kelava (2008), S.29 gewählten, da die Personen hier „befragt“ werden.
Tags: Definition, Test, Testarten
Quelle: F12
Quelle: F12
Wodurch sind Leistungstests gekennzeichnet? Beispiele?
Sind dadurch gekennzeichnet, dass sie



- Konstrukte erfassen, die sich auf kognitive Leistungen beziehen
- die unter der jeweiligen Testbedingung maximale Leistung erfassen möchten
- Aufgaben verwenden, bei denen es „richtige“ und „falsche“ Antworten gibt



Tags: Definition, Leistungstest, Test
Quelle: F13
Quelle: F13
Wodurch sind Persönlichkeitsfragebögen gekennzeichnet? Beispiel?
Sind dadurch gekennzeichnet, dass sie

- das Ziel verfolgen, das für eine Person typische Verhalten zu erfassen,
- mehrere Fragen verwenden, um das Persönlichkeitsmerkmal zu erfassen,
- die Antworten nicht in „richtig“ und „falsch“ klassifizierbar sind, sondern „erfragen“, wie stark das interessierende Merkmal ausgeprägt ist und
- im Allgemeinen leicht verfälschbar sind (z.B. durch sozial erwünschte Antworten).

Tags: Definition, Fragebogen, Persönlichkeitsfragebogen, Test
Quelle: F17
Quelle: F17
Was kennzeichnet objektive Persönlichkeitstests?
Sind dadurch gekennzeichnet, dass sie
(„Tarnen“ sich als Leistungstests, sind aber Persönlichkeitstests)
- versuchen, das Ausmaß an „Verfälschbarkeit“ z.B. durch „sozial erwünschte Antworten“ zu reduzieren indem sie
- das Persönlichkeitsmerkmal nicht durch subjektive Urteile, sondern über Verhalten in standardisierten Situationen erfassen.
(„Tarnen“ sich als Leistungstests, sind aber Persönlichkeitstests)
Tags: Definition, Objektiver Persönlichkeitstest, Persönlichkeitstest, Test
Quelle: F19
Quelle: F19
Was kennzeichnet projektive Tests?
Sind dadurch gekennzeichnet, dass sie



- versuchen, die Persönlichkeit als Ganzes zu erfassen, wobei sie
- auf individuelle Erlebnis- und Bedürfnisstrukturen Rücksicht nehmen,
- mehrdeutiges Bildmaterial verwenden, um unbewusste oder verdrängte Bewusstseinsinhalte zu erfassen und
- oft explorativen Charakter haben. (Man erhält keine konkrete Zahl)



Tags: Definition, projektiver Test, Test
Quelle: F20
Quelle: F20
Welche 2 Arten von apparative Tests werden unterschieden?
Moosbrugger & Kelava (2008), S. 32 unterscheiden im Wesentlichen zwei Arten
- Tests, sie insbesondere sensorische und motorische Merkmale erfassen. z.B.Tests zur - Erfassung von Muskelkraft- Geschicklichkeit- sensumotorischer Koordination
- computerbasierte Tests, die häufig spezielle Varianten von Leistungstests und Persönlichkeitsfragebogen sind.
Tags: apparativer Test, Definition, Test
Quelle: F24
Quelle: F24
Welche Testgütekritieren können unterschieden werden (im Überblick)?
Hauptgütekriterien
Nebengütekriterien
- Objektivität
- Reliabilität
- Validität
Nebengütekriterien
- Skalierung
- Normierung
- Ökonomie
- Nützlichkeit
- Zumutbarkeit
- Unverfälschbarkeit
- Fairness
Tags: Objektivität, Reliabilität, Testgütekriterien, Validität
Quelle: F26
Quelle: F26
Was versteht man unter Objektivität und welche 3 Bereiche lassen sich unterscheiden?
Ein Test ist objektiv, wenn er dasjenige Merkmal, das er misst, unabhängig von TestleiterIn, TestauswerterIn und von der Ergebnisinterpretation misst.
(angelehnt an Moosbrugger & Kelava, 2008, S. 8)
Bei der Objektivität lassen sich drei Bereiche unterscheiden
(angelehnt an Moosbrugger & Kelava, 2008, S. 8)
Bei der Objektivität lassen sich drei Bereiche unterscheiden
- Durchführungsobjektivität (~Testleiterunabhängigkeit*)
- Auswertungsobjektivität (~Verrechnungssicherheit*)
- Interpretationsobjektivität (~Interpretationseindeutigkeit*)
Tags: Definition, Objektivität
Quelle: F27
Quelle: F27
Was versteht man unter Durchführungsobjektivität?
Durchführungsobjektivität ist gegeben, wenn das Ergebnis der Testung nicht davon abhängt, welche TestleiterIn, die Testung durchgeführt.
Demnach sollte die Testvorgabe unter möglichst standardisierten Bedingungen stattfinden.
Diese werden optimiert indem
Demnach sollte die Testvorgabe unter möglichst standardisierten Bedingungen stattfinden.
Diese werden optimiert indem
- Instruktionen, die die TestleiterInnen geben, schriftlich festgehalten sind,
- die soziale Interaktion zwischen TestleiterIn und getesteter Person möglichst gering gehalten wird und
- die Untersuchungssituationen möglichst ähnlich sind.
Tags: Definition, Objektivität
Quelle: F29
Quelle: F29
Was versteht man unter Auswertungsobjektivität?
Ist gegeben, wenn beim Vorliegen der Antworten der Personen auf die Fragen (=Testprotokoll) jede(r) AuswerterIn zum selben numerischen Testergebnis kommt.
Die Auswertungsobjektivität kann erhöht/gesichert werden durch
Die Auswertungsobjektivität kann durch statistische Kennzahlen zur Beurteilerübereinstimmung (z.B. Cohens Kappa, Fleiss Kappa, Konkordanzkoeffizienten nach Kendall) erfasst werden.
Die Auswertungsobjektivität kann erhöht/gesichert werden durch
- das Vermeiden freier Antwortformate,
- klare Auswertungsregeln und
- die Verwendung von Multiple-Choice (Mehrfachauswahl) Antworten.
Die Auswertungsobjektivität kann durch statistische Kennzahlen zur Beurteilerübereinstimmung (z.B. Cohens Kappa, Fleiss Kappa, Konkordanzkoeffizienten nach Kendall) erfasst werden.
Tags: Definition, Objektivität
Quelle: F30
Quelle: F30
Was versteht man unter Interpretationsobjektivität?
Ist gegeben, wenn beim Vorliegen der Testergebnisse unterschiedliche „TestanwenderInnen“ zum selben „Schluss“ kommen.
Die Interpretationsobjektivität kann erhöht/gesichert werden
durch
* Ein Prozentrang (PR) gibt an wie viel Prozent der „Referenzpopulation“ diesen oder einen schlechteren Testwert erzielen.
Die Interpretationsobjektivität kann erhöht/gesichert werden
durch
- klare Regeln für die Interpretation,
- Vorhandensein von Normen und Normwerten
- der Verwendung von Prozenträngen*.
* Ein Prozentrang (PR) gibt an wie viel Prozent der „Referenzpopulation“ diesen oder einen schlechteren Testwert erzielen.
Tags: Definition, Objektivität
Quelle: F31
Quelle: F31
Was versteht man unter Reliabilität und welche Arten lassen sich unterscheiden?
Ein Test ist dann (vollständig) reliabel, wenn er das Merkmal, das er misst, exakt, d.h. ohne Messfehler, misst.
(angelehnt an Moosbrugger & Kelava, 2008, S. 11)
Die Reliabilität eines Tests gibt den Grad der Genauigkeit an, mit dem ein Test ein bestimmtes Merkmal misst.
Allerdings geht es nicht darum, ob der Test auch jenes Merkmal misst, das er zu messen vorgibt.
Es lassen sich drei/vier Arten der Reliabilität unterscheiden
Näheres zur Reliabilität im Rahmen der Lehrveranstaltungseinheiten zur klassischen Testtheorie
(angelehnt an Moosbrugger & Kelava, 2008, S. 11)
Die Reliabilität eines Tests gibt den Grad der Genauigkeit an, mit dem ein Test ein bestimmtes Merkmal misst.
Allerdings geht es nicht darum, ob der Test auch jenes Merkmal misst, das er zu messen vorgibt.
Es lassen sich drei/vier Arten der Reliabilität unterscheiden
- Retest - Reliabilität
- Paralleltest - Reliabilität
- Innere Konsistenz
- [Testhalbierungs- (Split Half-) Reliabilität]
Näheres zur Reliabilität im Rahmen der Lehrveranstaltungseinheiten zur klassischen Testtheorie
Tags: Definition, Reliabilität
Quelle: F32
Quelle: F32
Was versteht man unter Validität und welche Arten können unterschieden werden?
Ein Test gilt dann als valide („gültig“), wenn er das Merkmal, das er messen soll, auch wirklich misst.
(angelehnt an Moosbrugger & Kelava, 2008, S. 13)
Die Validität ist im Hinblick auf die Praxis, das wichtigste Gütekriterium. Mit Hilfe der Validität lässt sich klären
Es lassen sich vier Arten der Validität unterscheiden
Näheres zur Validität im Rahmen der Lehrveranstaltungseinheiten zur klassischen Testtheorie und Faktorenanalyse.
(angelehnt an Moosbrugger & Kelava, 2008, S. 13)
Die Validität ist im Hinblick auf die Praxis, das wichtigste Gütekriterium. Mit Hilfe der Validität lässt sich klären
- wie sehr eine Test wirklich das zu messende Merkmal misst (~„Konstruktvalidität“) und
- wie gut der Testkennwert „Verhaltensweisen“ außerhalb der Testsituation vorhersagen kann (~„Kriteriumsvalidität“).
Es lassen sich vier Arten der Validität unterscheiden
- Inhaltsvalidität
- Augenscheinvalidität
- Konstruktvalidität
- Kriteriumsvalidität
Näheres zur Validität im Rahmen der Lehrveranstaltungseinheiten zur klassischen Testtheorie und Faktorenanalyse.
Tags: Definition, Validität
Quelle: F34
Quelle: F34
Was versteht man unter dem Gütekriterium der Skalierung?
Ein Test erfüllt das Gütekriterium Skalierung, wenn die laut Verrechnungsregel resultierenden Testwerte die empirische Merkmalsrelation adäquat abbilden.
(Moosbrugger & Kelava, 2008, S. 18)
Näheres zur Skalierung im Rahmen der Lehrveranstaltungseinheiten zur modernen Testtheorie.
(Moosbrugger & Kelava, 2008, S. 18)
Näheres zur Skalierung im Rahmen der Lehrveranstaltungseinheiten zur modernen Testtheorie.
Tags: Skalierung, Testgütekriterien
Quelle: F36
Quelle: F36
Was versteht man unter Normierung und wann ist das Gütekriterium erfüllt?
Unter Normierung (Eichung) eines Tests versteht man, das Erstellen eines Bezugssystems, mit dessen Hilfe die Ergebnisse einer Testperson im Vergleich zu den Merkmalsausprägungen anderer Personen eindeutig eingeordnet und interpretiert werden können.
(Moosbrugger & Kelava, 2008, S. 19)
Ziel der Normierung ist es einen Rahmen für die Interpretation der (durch eine Person) erzielten Testergebnisse zu schaffen. Dies erfolgt dadurch, dass die Testergebnisse in Normwerte umgewandelt werden.
Weit verbreitete Normwerte sind z.B.

Das Gütekriterium der Normierung (Eichung) kann als erfüllt angesehen werden, wenn
(Moosbrugger & Kelava, 2008, S. 19)
Ziel der Normierung ist es einen Rahmen für die Interpretation der (durch eine Person) erzielten Testergebnisse zu schaffen. Dies erfolgt dadurch, dass die Testergebnisse in Normwerte umgewandelt werden.
Weit verbreitete Normwerte sind z.B.
- Prozentränge,
- z-Werte,
- Z-Werte,
- IQ-Werte und
- T-Werte (nicht zu verwechseln mit den t-Werten des t-Tests).

Das Gütekriterium der Normierung (Eichung) kann als erfüllt angesehen werden, wenn
- die Eichtabellen gültig (d.h. nicht veraltet) sind,
- die Population für die Eichtabellen definiert ist und
- die für die Erstellung der Eichtabellen herangezogene Stichprobe repräsentativ ist*.
Tags: Normierung, Testgütekriterien
Quelle: F37
Quelle: F37
Was versteht man unter einem Prozentrang?
Der Prozentrang gibt an, wie viel Prozent der Normierungsstichprobe einen Testwert erzielen, der niedriger oder maximal ebenso hoch ist, wie der Testwert xv der Testperson v. Der Prozentrang entspricht somit dem prozentualen Flächenanteil der Häufigkeitsverteilung der Bezugsgruppe, der am unteren Skalenende beginnt und nach oben hin durch den Testwert xv begrenzt wird.
(nach Moosbrugger & Kelava, 2008, S. 168)

Prozentränge sind als Normwerte insofern besonders hervorzuheben, als sie
(nach Moosbrugger & Kelava, 2008, S. 168)

Prozentränge sind als Normwerte insofern besonders hervorzuheben, als sie
- keine Intervallskalierung der Testkennwerte voraussetzen,
- keine Normalverteilung der Testwerte voraussetzen und
- eine inhaltlich einfache Interpretation des Testergebnisses darstellen.
Tags: Prozentränge
Quelle: F40
Quelle: F40
Was versteht man unter z-Werte? Und wie sind die anderen Normwerte ableitbar?
z-Werte (Standardmesswerte)
Jedem z-Wert ist genau ein Prozentrang zugeordnet und umgekehrt. Diese Zuordnungen können anhand der aus der Statistik bekannten z-Tabellen abgelesen werden.
Mit Hilfe von z-Werten können intervallskalierte, aber nicht normalverteilte Testkennwerte in normalverteilte Testkennwerte transformiert werden (=Flächentransformation).

Aus den z-Werten sind alle üblicherweise verwendeten Normwerte ableitbar, mittels


Überblick
- sind im Falle intervallskalierter und normalverteilter Testkennwerte - definiert durch:
- legen die relative Position des Testkennwerts der getesteten Person bezogen auf die Referenzpopulation dar,
- sind positiv bei überdurchschnittlichen Leistungen,
- sind negativ bei unterdurchschnittlichen Testleistungen und
- Null bei durchschnittlichen Leistungen

Jedem z-Wert ist genau ein Prozentrang zugeordnet und umgekehrt. Diese Zuordnungen können anhand der aus der Statistik bekannten z-Tabellen abgelesen werden.
Mit Hilfe von z-Werten können intervallskalierte, aber nicht normalverteilte Testkennwerte in normalverteilte Testkennwerte transformiert werden (=Flächentransformation).

Aus den z-Werten sind alle üblicherweise verwendeten Normwerte ableitbar, mittels


Überblick
| Norm | Mittelwert M | Streuung s |
| z-Werte | 0 | 1 |
| IQ-Werte | 100 | 15 |
| Z-Werte (Standardwerte/SW) | 100 | 10 |
| T-Werte | 50 | 10 |
| C-Werte | 5 | 2 |
| Stanine-Werte | 5 | 2 |
| Sten-Werte | 5,5 | 2 |
| Wertpunkte | 10 | 3 |
| Prozentränge | (50%) | (34,1%) |
Tags: Normierung, Testgütekriterien, z-Wert
Quelle: F43
Quelle: F43

Berechne folgende Werte:
- z-Wert
- IQ-Wert
- Z-Wert
- T-Wert

Überblick
| Norm | Mittelwert M | Streuung s |
| z-Werte | 0 | 1 |
| IQ-Werte | 100 | 15 |
| Z-Werte (auch: Standardwerte oder SW) | 100 | 10 |
| T-Werte | 50 | 10 |
Tags: Normierung, z-Wert
Quelle: F48
Quelle: F48
In welche 6 Schritte lässt sich die Testkonstruktion unterteilen?
- Planung
- Itemkonstruktion
- Erstellung der vorläufigen Testversion
- Erprobung an Stichprobe
- Itemanalyse und Überarbeitung
- Normierung (Eichung)
Die Konstruktionsschritte können wiederum in mehrere Bereiche eingeteilt werden.
Tags: Testkonstruktion
Quelle: F50
Quelle: F50
Welche 4 unterschiedliche Strategien gibt es zu Itemkonstruktion? Beschreibe diese.
- intuitive Konstruktion
- rationale Konstruktion
- externale (kriteriumsorientierte) Konstruktion
- internale (faktorenanalytische) Konstruktion
Intuitive Konstruktion
Auf eine intuitive Konstruktion der Items sollte nur zurückgegriffen werden, wenn der theoretische Kenntnisstand bezüglich des interessierenden Merkmals gering ist (nach Moosbrugger & Kelava, 2008, S. 36).
Demnach ist die Konstruktion der Items abhängig von der Intuition der des/der TestkonstrukteurIn.
Rationale Konstruktion
Bei einer rationalen Konstruktion besteht bereits eine elaborierte Theorie über die Differenziertheit von Personen hinsichtlich des interessierenden Merkmals.
Es ist wesentlich
- das Merkmal zu differenzieren und spezifizieren sowie
- Verhaltensindikatoren festzulegen.
Externale (kriteriumsorientierte) Konstruktion
Hierbei wird zunächst ein großer Itempool zusammengestellt und Personen vorgegeben, die sich in dem interessierenden, externalen Merkmal (Kriterium) stark unterscheiden.
Im Anschluss werden jene Items ausgewählt, die gut zwischen Gruppen mit unterschiedlichen Ausprägungen im Kriterium diskriminieren.
Zur Absicherung der Diskriminationsfähigkeit der Items sollte das Ergebnis der Itemauswahl an einer anderen Stichprobe überprüft werden.
Internale (faktorenanalytische) Konstruktion
Hierbei werden zunächst Items konstruiert, die hypothetischen Verhaltensdimensionen erfassen sollen.
Diese werden einer Stichprobe von Personen der interessierenden Zielgruppe vorgegeben.
Im Anschluss werden die Items einer Faktorenanalyse unterzogen und aufgrund der faktorenanalytischen Ergebnisse zu „Skalen“ zusammengefasst.
Tags: Itemkonstruktion
Quelle: F51
Quelle: F51
Welche weiteren Aspekte sind bei der Itemkonstruktion und Testentwicklung noch zu beachten?
Weitere Aspekte der Itemkonstruktion und Testentwicklung, wie
sind auf den Seiten 38 – 71 des Buchs von Moosbrugger & Kelava (2008) zu finden.
- Aufgabentypen und Antwortformate
- Fehlerquellen bei der Itembeantwortung
- Gesichtspunkte der Itemformulierung
- Erstellen der vorläufigen Testversion
- Erprobung der vorläufigen Testversion
sind auf den Seiten 38 – 71 des Buchs von Moosbrugger & Kelava (2008) zu finden.
Tags: Itemkonstruktion, Testkonstruktion
Quelle: F57
Quelle: F57
Was sind die Axiome der klassischen Testtheorie?
Im Rahmen der klassischen Testtheorie gelten laut Moosbrugger & Kelava (2008)* die folgenden Axiome:
* die angeführten Axiome unterscheiden sich von den üblicherweise angeführten.
Axiome sind nicht weiter zu hinterfragende Grundannahmen.
- das Existenzaxiom,
- das Verknüpfungsaxiom und
- das Unabhängigkeitsaxiom.
* die angeführten Axiome unterscheiden sich von den üblicherweise angeführten.
Axiome sind nicht weiter zu hinterfragende Grundannahmen.
Tags: Axiome, Klassische Testtheorie
Quelle: F59
Quelle: F59
Was besagt das Existenzaxiom?
Das Existenzaxiom besagt, dass ein „wahrer Wert“ (= true score) existiert. Dieser „wahre Wert“ ist der Erwartungswert der gemessenen Leistung einer Person.
Demnach gilt

(Im Rahmen der klassischen Testtheorie gelten laut Moosbrugger & Kelava (2008) die folgenden Axiome: das Existenzaxiom, das Verknüpfungsaxiom und das Unabhängigkeitsaxiom.)
Demnach gilt

(Im Rahmen der klassischen Testtheorie gelten laut Moosbrugger & Kelava (2008) die folgenden Axiome: das Existenzaxiom, das Verknüpfungsaxiom und das Unabhängigkeitsaxiom.)
Tags: Axiome, Existenzaxiom, Klassische Testtheorie
Quelle: F60
Quelle: F60
Was ist das Verknüpfungsaxiom?
Das Verknüpfungsaxiom besagt, dass sich die gemessene Leistung einer Person aus ihrem wahren Wert und dem Messfehler zusammensetzt.

Der Messfehler spielt in der klassischen Testtheorie eine zentrale Rolle. Sie wird daher auch oft als „Messfehlertheorie“ bezeichnet.
(Im Rahmen der klassischen Testtheorie gelten laut Moosbrugger & Kelava (2008) die folgenden Axiome: das Existenzaxiom, das Verknüpfungsaxiom und das Unabhängigkeitsaxiom.)

Der Messfehler spielt in der klassischen Testtheorie eine zentrale Rolle. Sie wird daher auch oft als „Messfehlertheorie“ bezeichnet.
(Im Rahmen der klassischen Testtheorie gelten laut Moosbrugger & Kelava (2008) die folgenden Axiome: das Existenzaxiom, das Verknüpfungsaxiom und das Unabhängigkeitsaxiom.)
Tags: Axiome, Klassische Testtheorie, Verknüpfungsaxiom
Quelle: F61
Quelle: F61
Was ist das Unabhängigkeitsaxiom?
Das Unabhängigkeitsaxiom besagt, dass der „wahre Wert“ einer Person und der bei der Messung entstandene Messfehler nicht korrelieren.

(Im Rahmen der klassischen Testtheorie gelten laut Moosbrugger & Kelava (2008) die folgenden Axiome: das Existenzaxiom, das Verknüpfungsaxiom und das Unabhängigkeitsaxiom.)

(Im Rahmen der klassischen Testtheorie gelten laut Moosbrugger & Kelava (2008) die folgenden Axiome: das Existenzaxiom, das Verknüpfungsaxiom und das Unabhängigkeitsaxiom.)
Tags: Axiome, Klassische Testtheorie, Unabhängigkeitsaxiom
Quelle: F62
Quelle: F62
Welche Zusatzannahmen gibt es neben den Axiomen bei der Klassischen Testtheorie?
Da bei Messfehlertheorien im allgemeinen angenommen wird, dass es sich bei dem Messfehler um eine Zufallsvariable handelt, muss das Unabhängigkeitsaxiom erweitert werden.


Tags: Axiome, Klassische Testtheorie
Quelle: F63
Quelle: F63
Was kann aus den Axiomen der klassischen Testtheorie gefolgert werden hinsichtlich Erwartungswert des Messfehlers, Varianz und Kovarianz der gemessenen Werte?

Tags: Axiome, Erwartungswert, Klassische Testtheorie, Kovarianz, Varianz
Quelle: F64
Quelle: F64
Was versteht man unter äquivalenten Messungen? Welche vier Zugänge gibt es?
(Klassische Testtheorie)
Äquivalente Messungen
Bei den äquivalenten Messungen geht es um die Frage, welche Voraussetzungen erfüllt sein müssen, um annehmen zu können, dass zwei Tests (oder auch Items), dasselbe psychologische Merkmal messen.
Es gibt hierfür vier unterschiedlich strenge „Zugänge“:
– Replikation,
– Parallelmessung
– - äquivalente Messungen und
- äquivalente Messungen und
– essentielle -äquivalente Messungen.
-äquivalente Messungen.
Replikation
Bei der Replikation wird gefordert, dass verschiedene Messinstrumente bei derselben Person zu exakt demselben Messergebnis kommen müssen, um von einer wiederholten Messung zu sprechen. Sie stellt somit die strengsten (und für die Praxis unrealistische) Forderungen.
Parallelmessung
Um eine Parallelmessung handelt es sich, wenn zwei Tests (oder Items), denselben Erwartungswert und die selbe Varianz besitzen.
Demnach gilt bei Parallelmessungen

Parallelmessungen erfassen das gleiche psychologische Merkmal gleich genau, da die Gleichheit der Varianzen der Messwerte auch gleiche Varianzen der Messfehler bedeutet.
Ein zu Test A paralleler Test wird in weiterer Folge mit A‘ bezeichnet.
 - äquivalente Messungen
- äquivalente Messungen
Um - äquivalente Messungen handelt es sich, wenn zwei Tests (oder Items), denselben Erwartungswert aber unterschiedliche Varianz besitzen.
- äquivalente Messungen handelt es sich, wenn zwei Tests (oder Items), denselben Erwartungswert aber unterschiedliche Varianz besitzen.
Demnach gilt bei - äquivalenten Messungen
- äquivalenten Messungen

 - äquivalente Messungen erfassen das gleiche Merkmal verschieden genau.
- äquivalente Messungen erfassen das gleiche Merkmal verschieden genau.
Essentiell äquivalente Messungen
äquivalente Messungen
Bei essentiell - äquivalente Messungen unterscheiden sich die Erwartungswerte zweier Tests (oder Items) um eine additive Konstante. Die Varianzen können ebenfalls verschieden sein.
- äquivalente Messungen unterscheiden sich die Erwartungswerte zweier Tests (oder Items) um eine additive Konstante. Die Varianzen können ebenfalls verschieden sein.
Demnach gilt bei essentiell - äquivalenten Messungen
- äquivalenten Messungen

Äquivalente Messungen
Bei den äquivalenten Messungen geht es um die Frage, welche Voraussetzungen erfüllt sein müssen, um annehmen zu können, dass zwei Tests (oder auch Items), dasselbe psychologische Merkmal messen.
Es gibt hierfür vier unterschiedlich strenge „Zugänge“:
– Replikation,
– Parallelmessung
–
 - äquivalente Messungen und
- äquivalente Messungen und– essentielle
 -äquivalente Messungen.
-äquivalente Messungen.Replikation
Bei der Replikation wird gefordert, dass verschiedene Messinstrumente bei derselben Person zu exakt demselben Messergebnis kommen müssen, um von einer wiederholten Messung zu sprechen. Sie stellt somit die strengsten (und für die Praxis unrealistische) Forderungen.
Parallelmessung
Um eine Parallelmessung handelt es sich, wenn zwei Tests (oder Items), denselben Erwartungswert und die selbe Varianz besitzen.
Demnach gilt bei Parallelmessungen

Parallelmessungen erfassen das gleiche psychologische Merkmal gleich genau, da die Gleichheit der Varianzen der Messwerte auch gleiche Varianzen der Messfehler bedeutet.
Ein zu Test A paralleler Test wird in weiterer Folge mit A‘ bezeichnet.
 - äquivalente Messungen
- äquivalente MessungenUm
 - äquivalente Messungen handelt es sich, wenn zwei Tests (oder Items), denselben Erwartungswert aber unterschiedliche Varianz besitzen.
- äquivalente Messungen handelt es sich, wenn zwei Tests (oder Items), denselben Erwartungswert aber unterschiedliche Varianz besitzen.Demnach gilt bei
 - äquivalenten Messungen
- äquivalenten Messungen
 - äquivalente Messungen erfassen das gleiche Merkmal verschieden genau.
- äquivalente Messungen erfassen das gleiche Merkmal verschieden genau.Essentiell
 äquivalente Messungen
äquivalente MessungenBei essentiell
 - äquivalente Messungen unterscheiden sich die Erwartungswerte zweier Tests (oder Items) um eine additive Konstante. Die Varianzen können ebenfalls verschieden sein.
- äquivalente Messungen unterscheiden sich die Erwartungswerte zweier Tests (oder Items) um eine additive Konstante. Die Varianzen können ebenfalls verschieden sein.Demnach gilt bei essentiell
 - äquivalenten Messungen
- äquivalenten Messungen
Tags: äquivalente Messungen, Klassische Testtheorie
Quelle: F65
Quelle: F65
Was ist die Reliabilität? Was kennzeichnet diese?
Die Reliabilität eines Tests gibt den Grad der Genauigkeit an, mit dem ein Test ein bestimmtes Merkmal misst. Im Rahmen der klassischen Testtheorie steht hierbei die Varianz des Messfehlers im Vordergrund.
Vereinfacht gesagt: Je größer die Varianz des Messfehlers desto, geringer die Reliabilität.

Je nach Autor wird eine Reliabilität ab 0.7 bzw. 0.8 als ausreichende Reliabilität angesehen.

Vereinfacht gesagt: Je größer die Varianz des Messfehlers desto, geringer die Reliabilität.

Je nach Autor wird eine Reliabilität ab 0.7 bzw. 0.8 als ausreichende Reliabilität angesehen.

Tags: Reliabilität
Quelle: F70
Quelle: F70
Welche Arten der Reliabilitätsbestimmung gibt es (im Überblick)?
Es lassen sich drei/vier Arten der Reliabilität unterscheiden
- Retest - Reliabilität
- Paralleltest – Reliabilität
- [Testhalbierungs- (Split Half-) Reliabilität]
- Innere Konsistenz
Tags: Reliabilität
Quelle: F73
Quelle: F73
Was versteht man unter der Retest-Reliabilität?
Hierbei wird derselbe Test derselben Stichprobe zweimal vorgelegt. Vorausgesetzt es gibt weder
entspricht die geschätzte Reliabilität der Korrelationen der Testergebnisse der beiden Durchgänge.
Um unsystematische Veränderungen handelt es sich, wenn die zeitlichen Veränderungen nicht bei allen Personen gleichartig sind z.B. bei manchen Personen bleibt der wahre Wert gleich bei anderen steigt er.
Bei Leistungstest ergeben sich Probleme z.B. aufgrund von Deckeneffekten.
- Veränderungen der Messfehlereinflüsse noch
- „unsystematische“ Veränderungen des wahren Werts,
entspricht die geschätzte Reliabilität der Korrelationen der Testergebnisse der beiden Durchgänge.
Um unsystematische Veränderungen handelt es sich, wenn die zeitlichen Veränderungen nicht bei allen Personen gleichartig sind z.B. bei manchen Personen bleibt der wahre Wert gleich bei anderen steigt er.
Bei Leistungstest ergeben sich Probleme z.B. aufgrund von Deckeneffekten.
Tags: Reliabilität
Quelle: F73
Quelle: F73
Was versteht man unter der Paralleltest-Reliabilität?
Hierbei werden den Personen zwei Tests vorgelegt, die parallele Messungen darstellen. Die Korrelation der Ergebnisse schätzt die Reliabilität der beiden Tests.

Probleme ergeben sich, wenn die beiden Tests nicht völlig parallel sind. Eine strenge Testung der Parallelität zweier Tests ist im Rahmen der klassischen Testtheorie nicht möglich.
Die eleganteste Prüfung der Parallelität von Tests ohne auf die moderne Testtheorie zurückzugreifen, stellen konfirmatorische Faktorenanalysen dar.

Probleme ergeben sich, wenn die beiden Tests nicht völlig parallel sind. Eine strenge Testung der Parallelität zweier Tests ist im Rahmen der klassischen Testtheorie nicht möglich.
Die eleganteste Prüfung der Parallelität von Tests ohne auf die moderne Testtheorie zurückzugreifen, stellen konfirmatorische Faktorenanalysen dar.
Tags: Reliabilität
Quelle: F74
Quelle: F74
Was ist die Testhalbierungs-Reliabilität (Split-Half Reliabilität)?
Hierbei wird ein aus mehreren Items bestehender Test in zwei möglichst parallele Untertests geteilt. Die Korrelation der Ergebnisse der beiden Untertests schätzt die Reliabilität des halb so langen Tests. Um auf die geschätzte Reliabilität des Gesamttests zu kommen, wird auf einen Spezialfall der Formel von Spearman-Brown* zurückgegriffen.


Tags: Reliabilität
Quelle: F75
Quelle: F75
Was ist die Innere Konsistenz?
Methode zur Feststellung der Reliabilität
Hierbei wird jedes Item eines aus mehreren Items bestehenden Tests als eigene Messung des interessierenden Merkmals betrachtet. Die innere Konsistenz kann dann vereinfacht als durchschnittliche Korrelation aller Items dieses Tests verstanden werden, hängt aber auch von der Anzahl an Items im Test ab.
Die bekanntesten Kennwerte zur inneren Konsistenz sind

Stellen die Items zumindest essentiell - äquivalente Messungen dar, sind
- äquivalente Messungen dar, sind  und
und 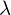 3 Schätzungen der Reliabilität des Gesamttests.
3 Schätzungen der Reliabilität des Gesamttests.
Für den Fall, dass die Items keine äquivalenten Messungen darstellen, sind und
und 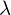 3 lediglich untere Schranken der Reliabilität.
3 lediglich untere Schranken der Reliabilität.
WICHTIG
Hierbei wird jedes Item eines aus mehreren Items bestehenden Tests als eigene Messung des interessierenden Merkmals betrachtet. Die innere Konsistenz kann dann vereinfacht als durchschnittliche Korrelation aller Items dieses Tests verstanden werden, hängt aber auch von der Anzahl an Items im Test ab.
Die bekanntesten Kennwerte zur inneren Konsistenz sind
- Cronbach

- Lambda3 nach Guttman

Stellen die Items zumindest essentiell
 - äquivalente Messungen dar, sind
- äquivalente Messungen dar, sind  und
und 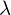 3 Schätzungen der Reliabilität des Gesamttests.
3 Schätzungen der Reliabilität des Gesamttests.Für den Fall, dass die Items keine äquivalenten Messungen darstellen, sind
 und
und 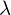 3 lediglich untere Schranken der Reliabilität.
3 lediglich untere Schranken der Reliabilität.WICHTIG
- bei der Berechnung von
 und
und 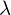 3 müssen die Items gleichartig „gepolt“ sein, d.h. hohe Werte müssen inhaltlich immer dieselbe Bedeutung haben (z.B. für eine hohe Ausprägung des Merkmals sprechen)
3 müssen die Items gleichartig „gepolt“ sein, d.h. hohe Werte müssen inhaltlich immer dieselbe Bedeutung haben (z.B. für eine hohe Ausprägung des Merkmals sprechen) - Weder
 noch
noch 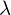 3 sind ein Maß für die „Eindimensionalität“ von Items
3 sind ein Maß für die „Eindimensionalität“ von Items
Tags: Reliabilität
Quelle: F76
Quelle: F76
Was kann man mit der Formel nach Spearman-Brown berechnen?
Für den Fall paralleler Items, kann aus der Kenntnis der Reliabilität eines Tests, die Reliabilität des um parallele Items verlängerten bzw. verkürzten Tests mittels der Formel von Spearman-Brown berechnet werden.


Tags: Reliabilität, Spearman-Brown
Quelle: F82
Quelle: F82
Ein Test besteht aus 30 parallelen Items.
Die Reliabilität des Tests beträgt rel=0.67
Wie hoch ist die Reliabilität, wenn man den Test um 10 parallele Items verlängert?
Die Reliabilität des Tests beträgt rel=0.67
Wie hoch ist die Reliabilität, wenn man den Test um 10 parallele Items verlängert?

Tags: Reliabilität, Spearman-Brown
Quelle: F83
Quelle: F83
Ein Test besteht aus 30 parallelen Items.
Die Reliabilität des Tests beträgt rel=0.67
Wie viele Items mehr benötigt der Test, wenn man eine Reliabilität von 0.73 anstrebt?
Die Reliabilität des Tests beträgt rel=0.67
Wie viele Items mehr benötigt der Test, wenn man eine Reliabilität von 0.73 anstrebt?

Tags: Reliabilität, Spearman-Brown
Quelle: F84
Quelle: F84
Wie verändern sich Mittelwert und Varianz bei der Verlängerung/Verkürzung von Tests?
Verlängert oder verkürzt man einen Test um parallele Items, können Mittelwert und Varianz des veränderten Tests aus Kenntnis der Kennwerte des Originaltests mittels der nachfolgenden Formeln errechnet werden.

verlängerter Test - Mittelwert höher
verkürzter Test - Mittelwert kleiner

verlängerter Test - Mittelwert höher
verkürzter Test - Mittelwert kleiner
Was ist die anzustrebende Höhe der Reliabilität? Welche Punkte sind zu berücksichtigen?
Allgemein: so hoch wie möglich.
Es sind jedoch die nachfolgenden Punkte zu berücksichtigen
Art des zu erfassenden Merkmals
Leistungsvariablen sind meist präziser messbar als z.B. Einstellungen oder Persönlichkeitseigenschaften. Bei etablierten Intelligenztests sind Reliabilitäten der globalen Maße oft über 0.90, während Persönlichkeitsfragebogen Skalen oft nur Reliabilitäten um 0.7 aufweisen.
Bei heterogenen Merkmalen kann die innere Konsistenz deutlich geringer sein als z.B. die Retest- oder Paralleltest Reliabilität.
Individual- versus Kollektivdiagnostik
Bei Individualdiagnostik sollte Messgenauigkeit höher sein als bei Messung der Durchschnittleistung eines Kollektivs, da sich die Messfehler bei der Zusammenfassung von Messungen mehrerer Individuen „reduzieren“.
Einsatzbedingungen
Bei Tests, die nicht adaptiv* vorgegeben werden können, hängt die Reliabilität relativ stark von der Testlänge ab.
Daher weisen Tests und Fragebögen, die zum Screening eingesetzt werden und daher eher kurz sind, meist eine geringere Reliabilität auf.
*adaptive Testvorgaben werden im Rahmen der Einheiten zur modernen Testtheorie behandelt
Es sind jedoch die nachfolgenden Punkte zu berücksichtigen
- Art des zu erfassenden Merkmals
- Individual- versus Kollektivdiagnostik
- Einsatzbedingungen
- Kosten-Nutzen Abwägungen
- Objektivierbarkeit
Art des zu erfassenden Merkmals
Leistungsvariablen sind meist präziser messbar als z.B. Einstellungen oder Persönlichkeitseigenschaften. Bei etablierten Intelligenztests sind Reliabilitäten der globalen Maße oft über 0.90, während Persönlichkeitsfragebogen Skalen oft nur Reliabilitäten um 0.7 aufweisen.
Bei heterogenen Merkmalen kann die innere Konsistenz deutlich geringer sein als z.B. die Retest- oder Paralleltest Reliabilität.
Individual- versus Kollektivdiagnostik
Bei Individualdiagnostik sollte Messgenauigkeit höher sein als bei Messung der Durchschnittleistung eines Kollektivs, da sich die Messfehler bei der Zusammenfassung von Messungen mehrerer Individuen „reduzieren“.
Einsatzbedingungen
Bei Tests, die nicht adaptiv* vorgegeben werden können, hängt die Reliabilität relativ stark von der Testlänge ab.
Daher weisen Tests und Fragebögen, die zum Screening eingesetzt werden und daher eher kurz sind, meist eine geringere Reliabilität auf.
*adaptive Testvorgaben werden im Rahmen der Einheiten zur modernen Testtheorie behandelt
Tags: Reliabilität
Quelle: F86
Quelle: F86
Was ist der Zusammenhang zwischen Reliabilität und Konfidenzintervallen? Welche Arten von Konfidenzintervallen gibt es?
Reliabilität und Konfidenzintervalle für 
Da die Reliabilität als Maß für die Genauigkeit der Messung des wahren Werts einer Person verstanden werden kann, ist sie Basis für die Erstellung von Konfidenzintervallen für wahre Werte.
Es gibt zwei Arten von Konfidenzintervallen
– auf Basis der Messfehlervarianz
– auf Basis der Schätzfehlervarianz

Da die Reliabilität als Maß für die Genauigkeit der Messung des wahren Werts einer Person verstanden werden kann, ist sie Basis für die Erstellung von Konfidenzintervallen für wahre Werte.
Es gibt zwei Arten von Konfidenzintervallen
– auf Basis der Messfehlervarianz
– auf Basis der Schätzfehlervarianz
Tags: Konfidenzintervalle, Reliabilität
Quelle: F90
Quelle: F90
Wie kann die Messfehlervarianz berechnet werden?
KI auf Basis der Messfehlervarianz
Bei Vorliegen der Varianz der Testwerte und der Reliabilität kann die Messfehlervarianz berechnet werden.

Bei Vorliegen der Varianz der Testwerte und der Reliabilität kann die Messfehlervarianz berechnet werden.

Tags: Konfidenzintervalle, Reliabilität
Quelle: F91
Quelle: F91
Wie kann der geschätzte wahre Wert und die Schätzfehlervarianz berechnet werden?
KI auf Basis der Schätzfehlervarianz


Tags: Konfidenzintervalle, Reliabilität, Varianz
Quelle: F92
Quelle: F92
Eine Person erzielt in einem Test 43 Punkte. Es ist bekannt, dass der Mittelwert des Tests 39 Punkte, die Standardabweichung des Tests 5 Punkte und die Reliabilität rel= 0.85 beträgt.
In welchem Bereich befindet sich der wahre Wert der Person mit 99%iger Sicherheit?
In welchem Bereich befindet sich der wahre Wert der Person mit 99%iger Sicherheit?

Tags: Mittelwert, Reliabilität, Standardabweichung, Varianz
Quelle: F93
Quelle: F93
Eine Person erzielt in einem Test einen IQ von 134. Die im Testmanual angegebene Testreliabilität beträgt rel= 0.75.
Kann man mit 95%iger Sicherheit davon ausgehen, dass die Person einen „wahren“ IQ über 130 hat und somit hochbegabt ist?
Bemerkung: die Standardabweichung des IQ ist laut Normtabellen auf 15 festgelegt
Kann man mit 95%iger Sicherheit davon ausgehen, dass die Person einen „wahren“ IQ über 130 hat und somit hochbegabt ist?
Bemerkung: die Standardabweichung des IQ ist laut Normtabellen auf 15 festgelegt

Tags: Konfidenzintervalle, Reliabilität
Quelle: F94
Quelle: F94
Was versteht man unter Validität?
Definition
Ein Test gilt dann als valide („gültig“), wenn er das Merkmal, das er messen soll, auch wirklich misst.
(angelehnt an Moosbrugger & Kelava, 2008, S. 13)
ABER:
Woran ist erkennbar welches Merkmal ein Test misst?
Anstatt von der „Validität eines Tests“ zu sprechen, sollte die Validität möglicher Interpretationen von Testergebnissen betrachtet werden.
(vergl. Moosbrugger & Kelava, 2008,S.136)
Ein Test gilt dann als valide („gültig“), wenn er das Merkmal, das er messen soll, auch wirklich misst.
(angelehnt an Moosbrugger & Kelava, 2008, S. 13)
ABER:
Woran ist erkennbar welches Merkmal ein Test misst?
Anstatt von der „Validität eines Tests“ zu sprechen, sollte die Validität möglicher Interpretationen von Testergebnissen betrachtet werden.
(vergl. Moosbrugger & Kelava, 2008,S.136)
Tags: Validität
Quelle: F95
Quelle: F95
Auf was können sich die verschiedenen Interpretationen eines Testergebnisses beziehen?
Verschiedene Interpretationen des Testergebnisses können sich beziehen auf
Entscheidungen als Folge des Testergebnisses ergeben.
Vor der Validierung muss überlegt werden, welche der oben angeführten Bereiche betrachtet werden sollen.
- die Bewertung des Endergebnisses,
- das Verallgemeinern des Ergebnisses,
- die Extrapolation auf andere Bereiche,
- das (kausale) Erklären und
- mögliche Konsequenzen, die sich durch das Treffen von
Entscheidungen als Folge des Testergebnisses ergeben.
Vor der Validierung muss überlegt werden, welche der oben angeführten Bereiche betrachtet werden sollen.
Tags: Validität
Quelle: F96
Quelle: F96
Welche Arten von Merkmalsdefinitionen können unterschieden werden?
(Validität)
Neben der Überlegung, welcher Bereich validiert werden soll, ist zu überlegen, auf welcher Definition das zu erfassende Merkmal basiert.
Moosbrugger & Kelava unterscheiden zwischen zwei Merkmalsdefinitionen
Die Grenzen zwischen den beiden Definitionen sind allerdings fließend.
Operationale Merkmalsdefinition
Um eine operationale Merkmalsdefinition handelt es sich, wenn die Testaufgaben den interessierenden Anforderungsbereich direkt repräsentieren.
Ein operational definiertes Merkmal bezieht sich zunächst nur auf die spezifischen Test- bzw. Merkmalsinhalte.
z.B.:
Theoretische Merkmalsdefinition
Bei theoretischen Merkmalsdefinitionen werden Theorien herangezogen, die spezifizieren (verdeutlichen), worauf bestimmte Unterschiede zwischen Personen zurückgeführt werden können und wie sich diese Unterschiede in den Testergebnissen ausdrücken.
z.B. formuliert Eysenck (1981) Annahmen darüber, in welchen neuronalen Strukturen sich Personen mit unterschiedlichen Ausprägungen der Persönlichkeitsdimension Extraversion unterscheiden. Daraus leitet er Unterschiede in bestimmten Erlebens- und Verhaltensweisen ab, auf die sich dann die Items, die zur Erfassung der Extraversion herangezogen werden, beziehen.
Neben der Überlegung, welcher Bereich validiert werden soll, ist zu überlegen, auf welcher Definition das zu erfassende Merkmal basiert.
Moosbrugger & Kelava unterscheiden zwischen zwei Merkmalsdefinitionen
- operational und
- theoretisch.
Die Grenzen zwischen den beiden Definitionen sind allerdings fließend.
Operationale Merkmalsdefinition
Um eine operationale Merkmalsdefinition handelt es sich, wenn die Testaufgaben den interessierenden Anforderungsbereich direkt repräsentieren.
Ein operational definiertes Merkmal bezieht sich zunächst nur auf die spezifischen Test- bzw. Merkmalsinhalte.
z.B.:
- Test zur Erfassung des Kurzzeitgedächtnisses
- Fragebogen zur Einschätzung der Sicherheit von Atomkraftwerken
Theoretische Merkmalsdefinition
Bei theoretischen Merkmalsdefinitionen werden Theorien herangezogen, die spezifizieren (verdeutlichen), worauf bestimmte Unterschiede zwischen Personen zurückgeführt werden können und wie sich diese Unterschiede in den Testergebnissen ausdrücken.
z.B. formuliert Eysenck (1981) Annahmen darüber, in welchen neuronalen Strukturen sich Personen mit unterschiedlichen Ausprägungen der Persönlichkeitsdimension Extraversion unterscheiden. Daraus leitet er Unterschiede in bestimmten Erlebens- und Verhaltensweisen ab, auf die sich dann die Items, die zur Erfassung der Extraversion herangezogen werden, beziehen.
Tags: Merkmal, Merkmalsdefinition, Validität
Quelle: F97
Quelle: F97
Welche Arten von Validität können unterschieden werden (im Überblick)? Welche weiteren Begriffe werden häufig im Zusammenhang mit Validität gebracht?
Im Wesentlichen werden vier Arten der Validität unterschieden
Weitere, häufig zu findende Begriffe im Zusammenhang mit Validität sind
- Inhaltsvalidität,
- Augenscheinvalidität,
- Kriteriumsvalidität und
- Konstruktvalidität.
Weitere, häufig zu findende Begriffe im Zusammenhang mit Validität sind
- Übereinstimmungsvalidität,
- prognostische Validität,
- diskriminante Validität und
- konvergente Validität.
Tags: Validität
Quelle: F100
Quelle: F100
Was versteht man unter Inhaltsvalidität?
Inhaltsvalidität bezieht sich darauf, inwieweit die Inhalte der Tests bzw. der Items, aus denen sich ein Test zusammensetzt, tatsächlich das interessierende Merkmal erfassen.
(vergl. Moosbrugger & Kelava, 2008, S.140)
Bei operationalisierten Merkmalen bezieht sich die Inhaltsvalidität vor allem auf die Verallgemeinerbarkeit der Testergebnisse. Es geht also darum, inwieweit die ausgewählte Items eine repräsentative Auswahl aus der Menge aller möglicher Aufgaben sind.
z.B. Wie gut decken die Fragen, die bei der Testtheorieprüfung gestellt werden, das vorgetragene Stoffgebiet ab?
Auch bei theoretisch definierten Merkmalen muss die Verallgemeinerung auf eine größere Menge von Aufgaben möglich sein. Zusätzlich muss angenommen werden können, dass unterschiedliche Antworten Unterschiede im interessierenden Merkmal erklären können.
Das bedeutet, es muss von den Antworten auf die Items auf das interessierende Merkmal geschlossen werden können.
Dies kann nur durch eine gute theoretische Fundierung und eine daran orientierte Itemkonstruktion gewährleistet werden.
(vergl. Moosbrugger & Kelava, 2008, S.140)
Bei operationalisierten Merkmalen bezieht sich die Inhaltsvalidität vor allem auf die Verallgemeinerbarkeit der Testergebnisse. Es geht also darum, inwieweit die ausgewählte Items eine repräsentative Auswahl aus der Menge aller möglicher Aufgaben sind.
z.B. Wie gut decken die Fragen, die bei der Testtheorieprüfung gestellt werden, das vorgetragene Stoffgebiet ab?
Auch bei theoretisch definierten Merkmalen muss die Verallgemeinerung auf eine größere Menge von Aufgaben möglich sein. Zusätzlich muss angenommen werden können, dass unterschiedliche Antworten Unterschiede im interessierenden Merkmal erklären können.
Das bedeutet, es muss von den Antworten auf die Items auf das interessierende Merkmal geschlossen werden können.
Dies kann nur durch eine gute theoretische Fundierung und eine daran orientierte Itemkonstruktion gewährleistet werden.
Tags: Validität
Quelle: F101
Quelle: F101
Was versteht man unter Augenscheinvalidität?
Augenscheinvalidität gibt an, inwieweit der Validitätsanspruch eines Tests vom bloßen Augenschein her einem Laien gerechtfertigt erscheint.
(Moosbrugger & Kelava, 2008 S.15)
(Moosbrugger & Kelava, 2008 S.15)
Tags: Validität
Quelle: F104
Quelle: F104
Was versteht man unter Konstruktvalidität? Wie wird diese untersucht?
Konstruktvalidität umfasst die empirischen Befunde und Argumente, mit denen die Zuverlässigkeit der Interpretation von Testergebnissen im Sinne erklärender Konzepte, die sowohl Testergebnisse als auch Zusammenhänge der Testwerte mit anderen Variablen erklären, gestützt wird.
(Messick, 1995, S.743, Übersetzung J. Hartig & A. Frey;
aus Moosbrugger & Kelava, 2008, S. 145)
Auf die Konstruktvalidität wird im Zuge der Faktorenanalyse nochmals eingegangen
Im Wesentlichen geht es darum, Testergebnisse vor dem Hintergrund eines theoretischen Konstrukts zu interpretieren.
Man unterscheidet zwischen
Der Bereich der Theorie beschäftigt sich mit nicht direkt beobachtbaren (=latenten) Konstrukten und deren Zusammenhängen. Im Idealfall sind diese Zusammenhänge durch Axiome formalisiert.
Korrespondenzregeln geben an, wie sich die theoretischen Zusammenhänge auf den Bereich des Beobachtbaren auswirken.
Bei diesen „Auswirkungen“ handelt es sich meist um Zusammenhänge zwischen manifesten Variablen mitunter aber auch um Unterschiede zwischen Gruppen.
Diese Zusammenhänge bzw. Unterschiede werden in weiterer Folge empirisch geprüft.
Stimmen die theoretische Vorhersagen mit den empirischen Beobachtungen überein, wird das als Bestätigung der Theorie als auch der Interpretation der Testkennwerte als individuelle Ausprägung auf dem theoretischen Konstrukt angesehen.
Für den Fall, dass eine relativ hohe Korrelation erwartet wird, spricht man von konvergenter Validität (z.B. Korrelation mit einem Test der dasselbe Konstrukt messen soll).
Falls man eine niedrige Korrelation erwartet, spricht man von diskriminanter Validität. (z.B. Korrelation mit einem Test, der ein anderes Konstrukt erfassen soll).
Weitere Methoden zur Untersuchung der Konstruktvalidität sind
Bei der Analyse von Antwortprozessen können Personen z.B. gebeten werden, bei der Bearbeitung der Aufgaben laut zu denken, um so Annahmen über Antwortprozesse zu erheben bzw. zu klären, ob sich die Antwortprozesse auf das gewünschte Konstrukt beziehen.
(Messick, 1995, S.743, Übersetzung J. Hartig & A. Frey;
aus Moosbrugger & Kelava, 2008, S. 145)
Auf die Konstruktvalidität wird im Zuge der Faktorenanalyse nochmals eingegangen
Im Wesentlichen geht es darum, Testergebnisse vor dem Hintergrund eines theoretischen Konstrukts zu interpretieren.
Man unterscheidet zwischen
- dem Bereich der Theorie und
- dem Bereich der Beobachtung.
Der Bereich der Theorie beschäftigt sich mit nicht direkt beobachtbaren (=latenten) Konstrukten und deren Zusammenhängen. Im Idealfall sind diese Zusammenhänge durch Axiome formalisiert.
Korrespondenzregeln geben an, wie sich die theoretischen Zusammenhänge auf den Bereich des Beobachtbaren auswirken.
Bei diesen „Auswirkungen“ handelt es sich meist um Zusammenhänge zwischen manifesten Variablen mitunter aber auch um Unterschiede zwischen Gruppen.
Diese Zusammenhänge bzw. Unterschiede werden in weiterer Folge empirisch geprüft.
Stimmen die theoretische Vorhersagen mit den empirischen Beobachtungen überein, wird das als Bestätigung der Theorie als auch der Interpretation der Testkennwerte als individuelle Ausprägung auf dem theoretischen Konstrukt angesehen.
Für den Fall, dass eine relativ hohe Korrelation erwartet wird, spricht man von konvergenter Validität (z.B. Korrelation mit einem Test der dasselbe Konstrukt messen soll).
Falls man eine niedrige Korrelation erwartet, spricht man von diskriminanter Validität. (z.B. Korrelation mit einem Test, der ein anderes Konstrukt erfassen soll).
Weitere Methoden zur Untersuchung der Konstruktvalidität sind
- Analysen von Antwortprozessen und
- der Vergleich von theoretisch erwarteten Itemschwierigkeiten mit empirisch ermittelten.
Bei der Analyse von Antwortprozessen können Personen z.B. gebeten werden, bei der Bearbeitung der Aufgaben laut zu denken, um so Annahmen über Antwortprozesse zu erheben bzw. zu klären, ob sich die Antwortprozesse auf das gewünschte Konstrukt beziehen.
Tags: Validität
Quelle: F105
Quelle: F105
Was versteht man unter Kriteriumsvalidität?
Kriteriumsvalidität bedeutet, dass von einem Testergebnis, auf ein für diagnostische Entscheidungen praktisch relevantes Kriterium außerhalb der Testsituation geschlossen werden kann. Kriteriumsvalidität kann durch empirische Zusammenhänge zwischen dem Testwert und möglichen Außenkriterien belegt werden. Je enger diese Zusammenhänge, desto besser kann die Kriteriumsvalidität als belegt gelten.
(Moosbrugger & Kelava, 2008, S. 156)
Von größter Bedeutung ist hierbei die Frage, welche Außenkriterien gewählt werden.
Die Auswahl sollte gut begründet und nachvollziehbar sein.
Kann ein theoretisch hergeleiteter Zusammenhang von Testergebnis und Außenkriterium empirisch untermauert werden, wird dadurch sowohl die Validität der theoriebasierten Testwertinterpretation als auch die Validität der diagnostischen Entscheidung unterstützt.
Außenkriterien können
(Moosbrugger & Kelava, 2008, S. 156)
Von größter Bedeutung ist hierbei die Frage, welche Außenkriterien gewählt werden.
Die Auswahl sollte gut begründet und nachvollziehbar sein.
Kann ein theoretisch hergeleiteter Zusammenhang von Testergebnis und Außenkriterium empirisch untermauert werden, wird dadurch sowohl die Validität der theoriebasierten Testwertinterpretation als auch die Validität der diagnostischen Entscheidung unterstützt.
Außenkriterien können
- zeitlich parallel existieren (Übereinstimmungsvalidität) oder
- sich auf zukünftige Ausprägungen eins Merkmals beziehen (prognostische Validität).
Tags: Validität
Quelle: F110
Quelle: F110
Wie kann die Kriteriumsvalidität berechnet werden? Welches Problem tritt dabei auf? Welche Formel muss hier angewendet werden?
Die praktische Berechnung der Kriteriumsvalidität erfolgt durch die Berechnung der Korrelation von Testergebnis (X) mit dem Außenkriterium (Y).

Problematisch dabei ist, dass die Validität durch zwei Messfehler „verdünnt“ wird. Sie fällt also aufgrund der Messfehler, die bei der Messung des Testergebnisses und des Außenkriteriums auftreten, geringer aus, als sie in „Wirklichkeit“ wäre.

Verdünnungsformeln
Um diesen Fehler auszugleichen, gibt es je nachdem welche(r) Messfehler theoretisch beseitigt werden soll, drei Verdünnungsformeln*

*die Verdünnungsformeln können natürlich auch im Zuge der Berechnung von Konstruktvaliditäten angewandt werden

Problematisch dabei ist, dass die Validität durch zwei Messfehler „verdünnt“ wird. Sie fällt also aufgrund der Messfehler, die bei der Messung des Testergebnisses und des Außenkriteriums auftreten, geringer aus, als sie in „Wirklichkeit“ wäre.

Verdünnungsformeln
Um diesen Fehler auszugleichen, gibt es je nachdem welche(r) Messfehler theoretisch beseitigt werden soll, drei Verdünnungsformeln*

*die Verdünnungsformeln können natürlich auch im Zuge der Berechnung von Konstruktvaliditäten angewandt werden
Tags: Validität, Verdünnungsformel
Quelle: F113
Quelle: F113
Die Korrelation eines Tests X mit einem Außenkriterium Y sei r(X,Y)=0.47. Es sei bekannt, dass die Reliabilität des Tests 0.64 und die des Außenkriteriums 0.49 beträgt.
Wie hoch wäre die Validität des Tests, wenn man das Außenkriterium fehlerfrei erheben könnte?
Wie hoch wäre die Validität des Tests, wenn man das Außenkriterium fehlerfrei erheben könnte?

Tags: Validität, Verdünnungsformel
Quelle: F116
Quelle: F116
Die Korrelation eines Tests X mit einem Außenkriterium Y sei
r(X,Y)=0.47. Es sei bekannt, dass die Reliabilität des Tests
0.64 und die des Außenkriteriums 0.49 beträgt.
Wie hoch wäre die Validität des Tests, wenn man das
Testergebnis fehlerfrei messen könnte?
r(X,Y)=0.47. Es sei bekannt, dass die Reliabilität des Tests
0.64 und die des Außenkriteriums 0.49 beträgt.
Wie hoch wäre die Validität des Tests, wenn man das
Testergebnis fehlerfrei messen könnte?

Tags: Validität, Verdünnungsformel
Quelle: F117
Quelle: F117
Die Korrelation eines Tests X mit einem Außenkriterium Y sei r(X,Y)=0.47. Es sei bekannt, dass die Reliabilität des Tests 0.64 und die des Außenkriteriums 0.49 beträgt.
Wie hoch wäre die Validität des Tests, wenn man sowohl den Test als auch das Außenkriterium fehlerfrei messen könnte?
Wie hoch wäre die Validität des Tests, wenn man sowohl den Test als auch das Außenkriterium fehlerfrei messen könnte?

Tags: Validität, Verdünnungsformel
Quelle: F118
Quelle: F118
Wie kann eine Kosten-Nutzen-Abwägung eines Tests erfolgen?
Ist die Validität eines Tests bekannt, kann damit der Nutzen der Anwendung eines Tests zur Personenselektion ermittelt werden.
Hierfür können die sogenannten Taylor- Russell Tafeln herangezogen werden.
Anhand der Taylor Russell Tafeln ist für tabellierte Grund- und Selektionsraten sowie bei gegebener Validität des Tests ablesbar, wie hoch der Anteil „wirklich geeigneter“ Personen ist, sofern sie aufgrund des Testergebnisses als „geeignet“ angesehen werden.
Hierfür können die sogenannten Taylor- Russell Tafeln herangezogen werden.
Anhand der Taylor Russell Tafeln ist für tabellierte Grund- und Selektionsraten sowie bei gegebener Validität des Tests ablesbar, wie hoch der Anteil „wirklich geeigneter“ Personen ist, sofern sie aufgrund des Testergebnisses als „geeignet“ angesehen werden.
Tags: Kosten-Nutzen, Taylor-Russell-Tafeln, Validität
Quelle: F119
Quelle: F119
Was ist die Grundidee der Taylor-Russel Tafeln?
Die Grundidee der Taylor Russel Tafeln besteht darin, dass angenommen wird, dass ein Individuum über eine bestimmte Mindestausprägung des zu erhebenden Merkmals verfügen muss, um für eine bestimmte Anforderung geeignet zu sein.
Je nachdem wie hoch diese Mindestausprägung ist, ist nur ein gewisser Prozentsatz der „relevanten“ Population „wirklich geeignet“. Dieser Prozentsatz nennt sich Grundrate (GR) bzw. Grundquote (GQ)
Weiters wird aufgrund des Testergebnisses ein bestimmter Teil der getesteten Personen als geeignet betrachtet. Dieser Anteil nennt sich Selektionsrate (SR) oder Selektionsquote (SQ).
Anhand der Taylor Russell Tafeln ist für tabellierte Grund und Selektionsraten sowie bei gegebener Validität des Tests ablesbar, wie hoch der Anteil „wirklich geeigneter“ Personen ist, sofern sie aufgrund des Testergebnisses als „geeignet“ angesehen werden (rosa Bereich).

Je nachdem wie hoch diese Mindestausprägung ist, ist nur ein gewisser Prozentsatz der „relevanten“ Population „wirklich geeignet“. Dieser Prozentsatz nennt sich Grundrate (GR) bzw. Grundquote (GQ)
Weiters wird aufgrund des Testergebnisses ein bestimmter Teil der getesteten Personen als geeignet betrachtet. Dieser Anteil nennt sich Selektionsrate (SR) oder Selektionsquote (SQ).
Anhand der Taylor Russell Tafeln ist für tabellierte Grund und Selektionsraten sowie bei gegebener Validität des Tests ablesbar, wie hoch der Anteil „wirklich geeigneter“ Personen ist, sofern sie aufgrund des Testergebnisses als „geeignet“ angesehen werden (rosa Bereich).

Tags: Taylor-Russell-Tafeln, Validität
Quelle: F120
Quelle: F120
Was zeigt diese Grafik?


- X-Achse: Testergebnis der Person
- Y-Achse: Merkmalsausprägung: Das Merkmal das wir messen wollen (z.B. Eignung für das Psychologiestudium)
- Gelb: idealisiertes Streudiagramm der gesamten Population
- Rote gepunktete Linie: Die Personen müssen hinsichtlich der Merkmalsausprägung über der Linie liegen. (Grundquote) - Rote Fläche: Leute die in Wirklichkeit geeignet sind.
- Grüne gepunktete Linie: Wenn die Person hinsichtlich des Testergebnisses über dieser Linie liegen, dann heißt dies, dass diese Personen laut dem Test geeignet sind. - Blaue Fläche: Leute die laut dem Test geeignet sind.
Es gibt einen Bereich/Gruppe an Personen die vom Test als geeignet gewählt werden, aber eigentlich nicht wirklich geeignet sind.
Der Überschneidungsbereich (rosa) beinhaltet alle Personen die geeignet sind und der Test als geeignet auswählt. (Bedingte Wahrscheinlichkeit)
Tags: Taylor-Russell-Tafeln, Validität
Quelle: F125
Quelle: F125
Inwiefern verändert die Validität die Form des Streudiagrams?


Die Validität bedingt die Form des Streudiagramms

- Die Ellipse symbolisiert die Korrelation zwischen der X-Variable (Testergebnis) und Y-Variable (Außenkriterium, Merkmal).
- Diese Validität ist die Kriteriumsvalidität. - Ist die Validität 0, dann ist das Streudiagramm eher rund. (kein Zusammenhang zwischen Testergebnis und Außenkriterium.- Ist die Validität 0,9, dann wird die Ellipse immer dünner.Der Anteil derer die durch den Test ausgewählt werden und tatsächlich geeignet sind wird immer höher.

Tags: Taylor-Russell-Tafeln, Validität
Quelle: F127
Quelle: F127
Was bedeutet ein Grundrate von 0,1?
Jeder 10. Ist geeignet (10% der Population).
(Taylor-Russel-Tafeln)
(Taylor-Russel-Tafeln)
Tags: Taylor-Russell-Tafeln, Validität
Quelle: F128
Quelle: F128
Was zeigt die Taylor-Russel-Tafel? (Spalten/Zeilen)

- Spaltenüberschrift – Selektionsrate: 0.05 – nur 5% der Personen die getestet werden, werden als geeignet anerkannt.
- Zeilenüberschrift (r): Validität des Tests
- In den Zellen: Wie viel Prozent der Personen die vom Test ausgewählt wurden sind tatsächlich geeignet.
Wenn man keinen Test nimmt und blind jemanden nimmt (raten), dann ist die Wahrscheinlichkeit die korrekte Person zu bekommen die Grundrate.
Tags: Taylor-Russell-Tafeln
Quelle: F128
Quelle: F128
Es sei bekannt, dass 40 % jener Personen, die sich für eine
Stelle bewerben auch wirklich dafür geeignet sind. Zur
Auswahl der Personen wird ein Test mit einer Validität von
val=0.20 verwendet.
a) Wie hoch ist die Wahrscheinlichkeit, dass die aus 20
BewerberInnen aufgrund des Tests ausgewählte Person
wirklich für die ausgeschriebene Stelle geeignet ist?
b) Wie hoch ist die Wahrscheinlichkeit eine geeignete
Person zu erhalten, wenn die Auswahl der Person nicht
aufgrund der Testergebnisse, sondern zufällig erfolgt?
Stelle bewerben auch wirklich dafür geeignet sind. Zur
Auswahl der Personen wird ein Test mit einer Validität von
val=0.20 verwendet.
a) Wie hoch ist die Wahrscheinlichkeit, dass die aus 20
BewerberInnen aufgrund des Tests ausgewählte Person
wirklich für die ausgeschriebene Stelle geeignet ist?
b) Wie hoch ist die Wahrscheinlichkeit eine geeignete
Person zu erhalten, wenn die Auswahl der Person nicht
aufgrund der Testergebnisse, sondern zufällig erfolgt?
a)
Lösung: GR= 0.40 SR=1/20=0.05 val=0.20
=> 0.57
b) Lösung: die Grundrate (hier 0.40)
Lösung: GR= 0.40 SR=1/20=0.05 val=0.20
=> 0.57
b) Lösung: die Grundrate (hier 0.40)
Tags: Taylor-Russell-Tafeln, Validität
Quelle: F129
Quelle: F129
Es sei bekannt, dass 40 % jener Personen, die sich für eine
Stelle bewerben auch wirklich dafür geeignet sind.
Wie hoch müsste die Validität sein, damit die
Wahrscheinlichkeit, dass eine aus 20 BewerberInnen
aufgrund des Tests ausgewählte Person, auch wirklich
geeignet ist, 95 % beträgt?
Stelle bewerben auch wirklich dafür geeignet sind.
Wie hoch müsste die Validität sein, damit die
Wahrscheinlichkeit, dass eine aus 20 BewerberInnen
aufgrund des Tests ausgewählte Person, auch wirklich
geeignet ist, 95 % beträgt?
Lösung: GR=0.40 SR=1/20=0.05 % - Satz=0.95
=> val= 0.70
=> val= 0.70
Tags: Taylor-Russell-Tafeln, Validität
Quelle: F132
Quelle: F132
Welche Grundannahme ist bei der Berechnung der Validität oder Reliabilität eines verkürzten/verlängerten Tests zu berücksichtigen?
Bei der Verkürzung eines Tests darf die Validität und Reliabilität nicht größer werden (und umgekehrt). Falls dies bei der Berechnung trotzdem herauskommt, dann soll dies angemerkt werden.
Tags: Reliabilität, Validität
Quelle: F133
Quelle: F133
Ein Test besteht aus 30 parallelen Items.
Die Reliabilität des Tests beträgt rel=0.67, die Validität ist 0.43.
Wie hoch ist die Validität, wenn man den Test um 10 parallele
Items verkürzt?
Die Reliabilität des Tests beträgt rel=0.67, die Validität ist 0.43.
Wie hoch ist die Validität, wenn man den Test um 10 parallele
Items verkürzt?

Tags: Validität
Quelle: F134
Quelle: F134
Was ist die Grundidee der Faktorenanalyse (einfaktoriell)?
Ziel der Faktorenanalyse: Fragen/Items die das Selbe erfassen zu einem Kennwert (Subskala, Skala) zusammenzufassen.
Korrelationen zwischen den (manifesten) Items werden dadurch erklärt, dass ihnen zumindest ein gemeinsames latentes Merkmal (=„Faktor“) zugrunde liegt.
Die paarweisen Korrelation zwischen den (standardisierten) Items sind selbst bei einem Faktor nicht 1, da neben dem
Einfluss des latenten Merkmals auch andere Einflüsse (wie z.B. Messfehler) berücksichtigt werden müssen.

Im Falle eines einzigen gemeinsamen latenten Merkmals, lautet die formale Darstellung der Faktorenanalyse

„itemspezifischer Faktor“ = Messfehler
Dieses Modell wird auch als das „Generalfaktormodell“ bezeichnet und geht auf Spearman zurück.
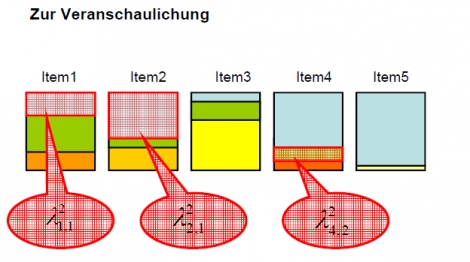
<b>
Zur Veranschaulichung</b>

Die Box steht für die Varianz des Items.
Die hellblaue Fläche für den Anteil an Varianz, der durch den ersten Faktor erklärt wird.
Die anderen Farben für die „itemspezifischen“ Einflüsse, die auf das jeweilige Item wirken. Sie sind bei jedem Item anders.
(Die Items 4 und 5 korrelieren am stärksten miteinander – da sie die größte Gemeinsamkeit haben.)
Korrelationen zwischen den (manifesten) Items werden dadurch erklärt, dass ihnen zumindest ein gemeinsames latentes Merkmal (=„Faktor“) zugrunde liegt.
Die paarweisen Korrelation zwischen den (standardisierten) Items sind selbst bei einem Faktor nicht 1, da neben dem
Einfluss des latenten Merkmals auch andere Einflüsse (wie z.B. Messfehler) berücksichtigt werden müssen.

Im Falle eines einzigen gemeinsamen latenten Merkmals, lautet die formale Darstellung der Faktorenanalyse

„itemspezifischer Faktor“ = Messfehler
Dieses Modell wird auch als das „Generalfaktormodell“ bezeichnet und geht auf Spearman zurück.
<b>
Zur Veranschaulichung</b>

Die Box steht für die Varianz des Items.
Die hellblaue Fläche für den Anteil an Varianz, der durch den ersten Faktor erklärt wird.
Die anderen Farben für die „itemspezifischen“ Einflüsse, die auf das jeweilige Item wirken. Sie sind bei jedem Item anders.
(Die Items 4 und 5 korrelieren am stärksten miteinander – da sie die größte Gemeinsamkeit haben.)
Beschreibe die Formel:


Im Falle eines einzigen gemeinsamen latenten Merkmals,
lautet die formale Darstellung der Faktorenanalyse

Zum Vergleich das Modell der einfachen Regression

lautet die formale Darstellung der Faktorenanalyse

Zum Vergleich das Modell der einfachen Regression

Tags: Faktorenanalyse, Regression
Quelle: F138
Quelle: F138
Was ist die Grundidee der Faktorenanalyse mit 2 Faktoren?

Zur Veranschaulichung

Die Box steht für die Varianz des Items.
Die hellblaue Fläche für den Anteil an Varianz, der durch den ersten Faktor erklärt wird.
Die hellgrünen Flächen für den Anteil an Varianz, der durch den
zweiten Faktor erklärt wird.
Die anderen Farben für die „itemspezifischen“ Einflüsse, die auf das jeweilige Item wirken. Sie sind bei jedem Item anders.
Tags: Faktorenanalyse
Quelle: F141
Quelle: F141
Was ist das multiple Faktorenmodell von Thurstone?
Wie lässt sich beruhend darauf die Korrelation zwischen zwei Items berechnen?
Wie lässt sich beruhend darauf die Korrelation zwischen zwei Items berechnen?


Tags: Faktorenanalyse, Korrelation
Quelle: F143
Quelle: F143
Wie hoch korrelieren folgende Items miteinander?
a) Item 1 und 3
b) Item 1 und 4

a) Item 1 und 3
b) Item 1 und 4

Multiple Faktorenanalyse - Korrelation zwischen Items

Die Berechnung kann sinnvoll sein um die Korrelation zu überprüfen wie es theoretisch ist (diese Berechnung) und realen Ergebnissen. Dies kann dabei helfen um zu überprüfen ob es möglicherweise noch einen weiteren, nicht entdeckten, Faktor gibt - wenn die theoretischen und realen Ergebnisse nicht übereinstimmen.
Um von einer Korrelation zu sprechen sollte der Unterschied nicht größer sein als 0.1

Die Berechnung kann sinnvoll sein um die Korrelation zu überprüfen wie es theoretisch ist (diese Berechnung) und realen Ergebnissen. Dies kann dabei helfen um zu überprüfen ob es möglicherweise noch einen weiteren, nicht entdeckten, Faktor gibt - wenn die theoretischen und realen Ergebnisse nicht übereinstimmen.
Um von einer Korrelation zu sprechen sollte der Unterschied nicht größer sein als 0.1
Tags: Faktorenanalyse, Korrelation
Quelle: F145
Quelle: F145
Tags: Faktorenanalyse, Kennwerte
Quelle: F146
Quelle: F146
Was versteht man unter der Ladung?
Ladungen der Faktoren pro Item


Ladung (Lambda) - Wichtig: Man liest dies von hinten (Faktor) nach vorne (Item)
-Ladung von Faktor 1 im Item 1
-Ladung von Faktor 1 im Item 2



Ladung (Lambda) - Wichtig: Man liest dies von hinten (Faktor) nach vorne (Item)
-Ladung von Faktor 1 im Item 1
-Ladung von Faktor 1 im Item 2
Tags: Faktorenanalyse, Ladung
Quelle: F147
Quelle: F147
Was versteht man unter Kommunalität eines Items?



Item 5: Die Kommunalität ist nur die hellblaue Fläche
Tags: Faktorenanalyse, Kennwert
Quelle: F150
Quelle: F150
Tags: Eigenwert, Faktorenanalyse, Kennwert
Quelle: F153
Quelle: F153
Tags: Eigenwert
Quelle: F154
Quelle: F154
Tags: Eigenwert, Kommunalität, Ladung
Quelle: F163
Quelle: F163
Berechne für folgende Werte die
- Eigenwerte?
- Prozent der Gesamtvarianz für Faktor 1 sowie Faktor 2?
- Prozent der erklärbaren Varianz für Faktor 1 und 2?

- Eigenwerte?
- Prozent der Gesamtvarianz für Faktor 1 sowie Faktor 2?
- Prozent der erklärbaren Varianz für Faktor 1 und 2?


Tags: Eigenwert, Varianz
Quelle: F164
Quelle: F164
Was ist die Grundidee der Parameterschätzung der Faktorenanalyse? Wie erfolgt die Parameterschätzung?
Die mathematische Herausforderung im Rahmen der Faktorenanalyse ist die Bestimmung der (unbekannten) Ladungen sowie die Festlegung der Faktorenzahl.
Die Grundidee der Parameterschätzung basiert darauf, zunächst jenen Faktor mit dem größten Eigenwert zu „extrahieren“. Dadurch wird die Summe der quadrierten verbleibenden Korrelationen zwischen den Items am stärksten minimiert.
Daraus folgt, dass man die Ladungen des 1. Faktors so bestimmt, dass

Die mathematische Name dieses Problems nennt sich „Eigenwert – Eigenvektor Problem“ und wurde (zum Glück) bereits gelöst.
Der Lösungsweg erfolgt iterativ und ist in realen Situationen für die händische Berechnung viel zu aufwändig.
Nach Extraktion des ersten Faktors (= Schätzung der Ladungen des ersten Faktors), wird der zweite Faktor nach derselben Grundidee extrahiert. Allerdings verwendet man hierfür nicht die originalen Korrelationen, sondern die um den Einfluss des ersten Faktors reduzierten. Diese Korrelationen werden „Restkorrelationen“ genannt.

Die Grundidee der Parameterschätzung basiert darauf, zunächst jenen Faktor mit dem größten Eigenwert zu „extrahieren“. Dadurch wird die Summe der quadrierten verbleibenden Korrelationen zwischen den Items am stärksten minimiert.
Daraus folgt, dass man die Ladungen des 1. Faktors so bestimmt, dass

Die mathematische Name dieses Problems nennt sich „Eigenwert – Eigenvektor Problem“ und wurde (zum Glück) bereits gelöst.
Der Lösungsweg erfolgt iterativ und ist in realen Situationen für die händische Berechnung viel zu aufwändig.
Nach Extraktion des ersten Faktors (= Schätzung der Ladungen des ersten Faktors), wird der zweite Faktor nach derselben Grundidee extrahiert. Allerdings verwendet man hierfür nicht die originalen Korrelationen, sondern die um den Einfluss des ersten Faktors reduzierten. Diese Korrelationen werden „Restkorrelationen“ genannt.

Tags: Faktorenanalyse, Parameterschätzung
Quelle: F165
Quelle: F165
Welche Extraktionsverfahren für die Parameterschätzung der Faktorenanalyse sind die am häufigsten angewandten?
Im Rahmen der Faktorenanalyse wurden eine Vielzahl an Extraktionsverfahren entwickelt. Die zwei am häufigsten angewandten sind
– die Hauptachsenanalyse („principal axis“) und
– die Hauptkomponentenanalyse („principal components“).
Bei der Hauptkomponentenanalyse wird davon ausgegangen, dass sich die Varianz eines Items vollständig durch die gemeinsamen Faktoren erklären lässt. Demnach sind alle Kommunalitäten (und somit auch die Korrelationen eines Items mit sich selbst) gleich 1. Als Konsequenz werden so viele Faktoren extrahiert, wie es Items gibt.
Sie ist die Standardeinstellung bei Berechnung einer Faktorenanalyse in SPSS.
Bei der Hauptachsenanalyse wird davon ausgegangen, dass sich die Varianz eines Items immer in die Kommunalität und die Einzelrestvarianz aufteilt. Demnach sind die Kommunalitäten (und somit auch die Korrelationen eines Items mit sich selbst) kleiner als 1.
Ziel ist es also, nur die durch die gemeinsamen Faktoren erklärbare Varianz zu beschreiben.
Da zu Beginn der Datenanalyse die Kommunalitäten nicht bekannt sind (=„Kommunalitätenproblem“), werden die Faktoren zunächst mittels Hauptkomponentenanalyse geschätzt und iterativ (=schrittweise) „verbessert“ („Kommunalitäteniteration“).
Kommunalitätenproblem - Vorgehensweise:
- „1“ wird in die Hauptdiagnoale geschrieben (jedes Items mit sich selbst)
- Mit der Lösung erhält man (etwas falsche) Ladungen
- Durch diese Ladungen erhält man (falsche) Kommunalitäten.
- Diese setzt man dann wiederrum in die Hauptdiagonale ein und führt die gesamte Berechnung neu durch.
- Dadurch kommt man zu immer besseren Daten.
Laut Backhaus et al.* unterscheidet sich die Interpretation der Faktoren je nach Methode.
Bei der Hauptkomponentenanalyse geht es darum, die hoch auf einem Faktor ladenden Items zu einem Sammelbegriff zusammenzufassen.
Bei der Hauptachsenanalyse geht es darum, die „Ursachen“ für die (hohen) Korrelationen zwischen den Items zu finden.
Mathematisch sind dies 2 leicht verschiedene Modelle, dies ist aber nicht weiter zu beachten (State of the art – in der Literatur wird immer die Hauptachsenanalyse erklärt – aber bei SPSS mit der Hauptkomponentenanalyse berechnet.
– die Hauptachsenanalyse („principal axis“) und
– die Hauptkomponentenanalyse („principal components“).
Bei der Hauptkomponentenanalyse wird davon ausgegangen, dass sich die Varianz eines Items vollständig durch die gemeinsamen Faktoren erklären lässt. Demnach sind alle Kommunalitäten (und somit auch die Korrelationen eines Items mit sich selbst) gleich 1. Als Konsequenz werden so viele Faktoren extrahiert, wie es Items gibt.
Sie ist die Standardeinstellung bei Berechnung einer Faktorenanalyse in SPSS.
Bei der Hauptachsenanalyse wird davon ausgegangen, dass sich die Varianz eines Items immer in die Kommunalität und die Einzelrestvarianz aufteilt. Demnach sind die Kommunalitäten (und somit auch die Korrelationen eines Items mit sich selbst) kleiner als 1.
Ziel ist es also, nur die durch die gemeinsamen Faktoren erklärbare Varianz zu beschreiben.
Da zu Beginn der Datenanalyse die Kommunalitäten nicht bekannt sind (=„Kommunalitätenproblem“), werden die Faktoren zunächst mittels Hauptkomponentenanalyse geschätzt und iterativ (=schrittweise) „verbessert“ („Kommunalitäteniteration“).
Kommunalitätenproblem - Vorgehensweise:
- „1“ wird in die Hauptdiagnoale geschrieben (jedes Items mit sich selbst)
- Mit der Lösung erhält man (etwas falsche) Ladungen
- Durch diese Ladungen erhält man (falsche) Kommunalitäten.
- Diese setzt man dann wiederrum in die Hauptdiagonale ein und führt die gesamte Berechnung neu durch.
- Dadurch kommt man zu immer besseren Daten.
Laut Backhaus et al.* unterscheidet sich die Interpretation der Faktoren je nach Methode.
Bei der Hauptkomponentenanalyse geht es darum, die hoch auf einem Faktor ladenden Items zu einem Sammelbegriff zusammenzufassen.
Bei der Hauptachsenanalyse geht es darum, die „Ursachen“ für die (hohen) Korrelationen zwischen den Items zu finden.
Mathematisch sind dies 2 leicht verschiedene Modelle, dies ist aber nicht weiter zu beachten (State of the art – in der Literatur wird immer die Hauptachsenanalyse erklärt – aber bei SPSS mit der Hauptkomponentenanalyse berechnet.
Tags: Faktorenanalyse, Parameterschätzung
Quelle: F168
Quelle: F168
Welche Methoden (5) gibt es um die Anzahl der Faktoren bei der Parameterschätzung festzulegen?
Für die Bestimmung der Anzahl an Faktoren gibt es fünf üblicherweise herangezogene Kriterien
Für die Bestimmung der Faktorenzahl gibt es keine generellen Vorschriften, sodass der Grad an Subjektivität hier relativ hoch ist.
- Faktorenzahl wird a priori festgelegt
- alle Restkorrelationen sind nahe 0 (z.B.: <.2)
- der Eigenwert des zuletzt extrahierten Faktors ist kleiner 1* (auch "Kaiser-Kriterium": im übertragenen Sinn ist damit die „Information, die über den Faktor vorliegt“ geringer als die Information eines einzigen Items), Ein Item hat die Varianz 1; wenn ein Faktor einen Eigenwert von weniger als 1 hat, dann enthält der Faktor weniger Information als ein einziges Item. Es macht dann keinen Sinn diesen Faktor zu verwenden.
- der Verlauf des Eigenwertediagramms (Screeplot) Bei der Betrachtung des Eigenwertediagramms, wird jene Stelle gesucht, an der Verlauf das Eigenwertediagramm „abflacht“ (= Elbow Kriterium). Die Faktoren vor dem „Knick“ werden in der weiteren Analyse berücksichtigt.
- die Parallelanalyse Bei der Parallelanalyse werden zumindest 100 Datensätze von Zufallszahlen erzeugt, wobei die Anzahl an Items und der Stichprobenumfang dem empirisch gewonnenen Datensatz entspricht. All diese Datensätze werden einer Faktorenanalyse unterzogen und die aus jeder Analyse gewonnenen Eigenwerte werden pro Faktor gemittelt. Als relevante nichttriviale Faktoren werden all jene Faktoren bezeichnet, deren Eigenwerte über jenen der (gemittelten) Eigenwerte der Parallelanalyse liegen.Dort wo die Parallelanalyse (zufällige Werte) die realen Eigenwerte schneidet, dort liegt die Grenze. PROBLEM: sehr aufwändig.

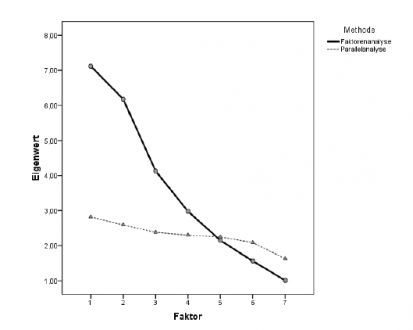
Für die Bestimmung der Faktorenzahl gibt es keine generellen Vorschriften, sodass der Grad an Subjektivität hier relativ hoch ist.
Tags: Faktorenanalyse, Faktorenzahl, Parameterschätzung
Quelle: F173
Quelle: F173
Wie erfolgt die Interpretation bei der Faktorenlösung (Ergebnisinterpretation)?
Die Ladungsmatrix bildet die Grundlage für die inhaltliche Interpretation der Faktoren. Hierfür werden üblicherweise die in einem Faktor hoch (=ideal sind Items mit Ladungen über 0.7) und in allen anderen Faktoren niedrig ladenden Items (ideal sind hier Ladungen unter 0.3) herangezogen. Diese Items werden auch als „Marker-Items“ bezeichnet.
Zeichnet man die Items als Punkte in einem Raum mit so vielen Dimensionen wie es Faktoren gibt, so liegen „Marker-Items“ „nahe“ an den Koordinatenachsen.
Vorgehen:
- Man nimmt Items die in einem Faktor hoch laden = Marker-Items
- Diese sollten im Idealfall in anderen Items niedrig laden.
- Bei diesen Items sollte man die Eigenschaft dann gut erkennen.
Wegen der Vorgehensweise bei der Parameterschätzung sind derartig hohe Ladungen bei der „Erstlösung“ in der Praxis aber eher selten.
Aus diesem Grund werden die Faktoren zur besseren Interpretierbarkeit „rotiert“.
Ziel ist eine einfache Struktur („simple structure“) bei der jedes Item nach Möglichkeit nur in einem Faktor hoch in den anderen Faktoren jedoch gering lädt.
Dadurch ergeben sich neue, besser interpretierbare Ladungen.
Zeichnet man die Items als Punkte in einem Raum mit so vielen Dimensionen wie es Faktoren gibt, so liegen „Marker-Items“ „nahe“ an den Koordinatenachsen.
Vorgehen:
- Man nimmt Items die in einem Faktor hoch laden = Marker-Items
- Diese sollten im Idealfall in anderen Items niedrig laden.
- Bei diesen Items sollte man die Eigenschaft dann gut erkennen.
Wegen der Vorgehensweise bei der Parameterschätzung sind derartig hohe Ladungen bei der „Erstlösung“ in der Praxis aber eher selten.
Aus diesem Grund werden die Faktoren zur besseren Interpretierbarkeit „rotiert“.
Ziel ist eine einfache Struktur („simple structure“) bei der jedes Item nach Möglichkeit nur in einem Faktor hoch in den anderen Faktoren jedoch gering lädt.
Dadurch ergeben sich neue, besser interpretierbare Ladungen.
Tags: Faktorenanalyse, Parameterschätzung
Quelle: F178
Quelle: F178
Was sind Marker-Items für Faktor 1 und für Faktor 2?
Was ist der nächste Schritt um eine Interpretation der Faktoren zu ermöglichen?

Was ist der nächste Schritt um eine Interpretation der Faktoren zu ermöglichen?

- Marker-Items für Faktor 1: 2,3,4,6
- Marker-Items für Faktor 2: 1,5 und 7 - Diese liegen in der Grafik nahe der Koordinatenachse F2
Ladungen – man sieht ein rechtwinkeliges Dreieck – wenn die orange Linie mittels der beiden Ladungen berechnet wird, ist das Ergebnis die Kommunalität (Ursprung zu Item). = Notwendig für Faktorenrotation.
Die Items liegen nicht auf den Achsen - Faktorenrotation
Ziel: Man dreht die Achsen, damit die Achsen auf den Items liegen– jedoch darf sich die Entfernung vom Mittelpunkt zu den Items (= Kommunalität) nicht ändern.
Tags: Faktorenanalyse, Marker-Item
Quelle: F178
Quelle: F178
Wie erfolgt die Faktorenrotation? Was ändert sich dadurch? Was bleibt gleich?
Wegen der Vorgehensweise bei der Parameterschätzung sind derartig hohe Ladungen bei der „Erstlösung“ in der Praxis aber eher selten.
Aus diesem Grund werden die Faktoren zur besseren Interpretierbarkeit „rotiert“.
Ziel ist eine einfache Struktur („simple structure“) bei der jedes Item nach Möglichkeit nur in einem Faktor hoch in den anderen Faktoren jedoch gering lädt.
Dadurch ergeben sich neue, besser interpretierbare Ladungen.

Durch die Rotation ändern sich
Unverändert bleiben
Aus diesem Grund werden die Faktoren zur besseren Interpretierbarkeit „rotiert“.
Ziel ist eine einfache Struktur („simple structure“) bei der jedes Item nach Möglichkeit nur in einem Faktor hoch in den anderen Faktoren jedoch gering lädt.
Dadurch ergeben sich neue, besser interpretierbare Ladungen.

Durch die Rotation ändern sich
- die Ladungen,
- die Eigenwerte und
- möglicherweise auch die Interpretation der Faktoren.
Unverändert bleiben
- die Kommunalitäten und
- der Anteil der durch die Faktoren erklärbaren Varianz.
Tags: Faktorenanalyse, Faktorenrotation
Quelle: F180
Quelle: F180
Welche Arten von Faktorenrotationen können unterschieden werden?
Wird der rechte Winkel zwischen den Faktorenachsen beibehalten (= unabhängige Faktoren) spricht man von einer orthogonalen Rotation.
Gibt man die Forderung nach unabhängigen Faktoren auf (=Faktorenachsen müssen nicht im rechten Winkel aufeinander stehen) so spricht man von schiefwinkeligen (= oblique) Rotationen.
Die bekannteste Art der Faktorenrotation ist die „Varimax-Rotation“. Hierbei werden die Faktoren so rotiert, dass die Varianz der Ladungen innerhalb eines Faktors maximal wird. Das bedeutet, das Ziel ist pro Faktor sowohl hohe als auch niedrige Ladungen zu haben, um so die Faktoren leichter benennen zu können.
Rechtwinkelig bedeutet unabhängig. Wenn man schiefwinkelige Faktorenlösungen nimmt, dann sind die Faktoren miteinander korreliert.

Gibt man die Forderung nach unabhängigen Faktoren auf (=Faktorenachsen müssen nicht im rechten Winkel aufeinander stehen) so spricht man von schiefwinkeligen (= oblique) Rotationen.
Die bekannteste Art der Faktorenrotation ist die „Varimax-Rotation“. Hierbei werden die Faktoren so rotiert, dass die Varianz der Ladungen innerhalb eines Faktors maximal wird. Das bedeutet, das Ziel ist pro Faktor sowohl hohe als auch niedrige Ladungen zu haben, um so die Faktoren leichter benennen zu können.
Rechtwinkelig bedeutet unabhängig. Wenn man schiefwinkelige Faktorenlösungen nimmt, dann sind die Faktoren miteinander korreliert.

Tags: Faktorenanalyse, Faktorenrotation
Quelle: F184
Quelle: F184
Was sind Faktorwerte? Welche Arten können unterschieden werden?
Da es das Ziel der Faktorenanalyse ist, die Zahl der Kennwerte zu reduzieren (aus vielen Items sollen deutlich weniger Faktoren resultieren), ist es nötig, Kennwerte für die Ausprägungen der Personen in den zu Grunde liegenden Faktoren zu ermitteln. Diese Kennwerte nennen sich Faktorwerte (auch „Skalenwerte“ genannt).
Man unterscheidet zwischen gewichteten und ungewichteten Faktorwerten.
Ungewichtete Faktorwerte
Die Berechnung der ungewichteten Faktorwerte erfolgt pro Person z.B. durch aufsummieren oder mitteln der Punkte jener Items, die in einem Faktor hoch laden.
Items, die in mehreren Faktoren ähnlich hohe Ladungen aufweisen, werden entweder jenem Faktor zugerechnet, in dem sie die höchste Ladung aufweisen oder bei der Berechnung der Faktorwerte nicht berücksichtigt.
Ist die Ladung eines Items in einem Faktor negativ, so muss das Item „umgepolt“ werden.
Gewichtete Faktorwerte
Da bei der ungewichteten Berechnung der Faktorwerte die unterschiedliche Konstruktvalidität der Items nicht berücksichtigt wird und Items, die in zwei oder mehr Faktoren ähnlich hohe Ladungen haben, problematisch sind, werden die Items je nach Ladung eines Items in einem Faktor gewichtet.

Man unterscheidet zwischen gewichteten und ungewichteten Faktorwerten.
Ungewichtete Faktorwerte
Die Berechnung der ungewichteten Faktorwerte erfolgt pro Person z.B. durch aufsummieren oder mitteln der Punkte jener Items, die in einem Faktor hoch laden.
Items, die in mehreren Faktoren ähnlich hohe Ladungen aufweisen, werden entweder jenem Faktor zugerechnet, in dem sie die höchste Ladung aufweisen oder bei der Berechnung der Faktorwerte nicht berücksichtigt.
Ist die Ladung eines Items in einem Faktor negativ, so muss das Item „umgepolt“ werden.
Gewichtete Faktorwerte
Da bei der ungewichteten Berechnung der Faktorwerte die unterschiedliche Konstruktvalidität der Items nicht berücksichtigt wird und Items, die in zwei oder mehr Faktoren ähnlich hohe Ladungen haben, problematisch sind, werden die Items je nach Ladung eines Items in einem Faktor gewichtet.
- Das Umpolen der Items ist hierbei nicht nötig.
- Es resultieren pro Faktor standardisierte Faktorwerte.
- Für die Berechnung stehen in SPSS unterschiedliche Methoden zu Verfügung.

Tags: Faktorenanalyse, Faktorwerte
Quelle: F188
Quelle: F188
Berechne die ungewichteten Faktorwerte für die 2 Faktoren:


Aufgrund der negativen Ladung von Item 5 in Faktor 1 muss dieses Item für die Berechnung des ungewichteten Faktorwerts (und auch für die Berechnung der Reliabilität) „umgepolt“ werden.








Tags: Faktorenanalyse, Faktorwert
Quelle: F190
Quelle: F190
Welche Arten der Faktorenanalyse können unterschieden werden?
Es lassen sich zwei Arten von Faktorenanalysen unterscheiden
Explorative Faktorenanalysen
Die explorative Faktorenanalyse wird verwendet, wenn noch keine Hypothesen über die Anzahl an Faktoren und die Zuordnung der Items zu den Faktoren existieren.
Die Zahl der Faktoren und die Zuordnung der Items zu den Faktoren wird mittels der zuvor besprochenen Vorgehensweisen bestimmt.
Konfirmatorische Faktorenanalysen
Bei der konfirmatorischen Faktorenanalyse sollen eine oder mehrere zuvor theoretisch festgelegte Faktorenstrukturen anhand empirischer Daten auf ihre Gültigkeit hin überprüft werden. Demnach müssen die Faktorenzahl und die Zuordnung der Items zu den Faktoren bekannt sein.
Die konfirmatorische Faktorenanalyse zählt zu den Strukturgleichungsmodellen (SEM) in deren Rahmen geprüft wird, wie gut ein oder mehrere theoretisch formulierte Modelle, die erhobenen Daten beschreiben. Für diese Fragestellung werden sowohl Signifikanztests als auch Indices zur Überprüfung der Modellanpassung an die Daten verwendet.
- die explorative und
- die konfirmatorische Faktorenanalyse.
Explorative Faktorenanalysen
Die explorative Faktorenanalyse wird verwendet, wenn noch keine Hypothesen über die Anzahl an Faktoren und die Zuordnung der Items zu den Faktoren existieren.
Die Zahl der Faktoren und die Zuordnung der Items zu den Faktoren wird mittels der zuvor besprochenen Vorgehensweisen bestimmt.
Konfirmatorische Faktorenanalysen
Bei der konfirmatorischen Faktorenanalyse sollen eine oder mehrere zuvor theoretisch festgelegte Faktorenstrukturen anhand empirischer Daten auf ihre Gültigkeit hin überprüft werden. Demnach müssen die Faktorenzahl und die Zuordnung der Items zu den Faktoren bekannt sein.
Die konfirmatorische Faktorenanalyse zählt zu den Strukturgleichungsmodellen (SEM) in deren Rahmen geprüft wird, wie gut ein oder mehrere theoretisch formulierte Modelle, die erhobenen Daten beschreiben. Für diese Fragestellung werden sowohl Signifikanztests als auch Indices zur Überprüfung der Modellanpassung an die Daten verwendet.
Tags: Faktorenanalyse
Quelle: F198
Quelle: F198
Was sind die Probleme, Grenzen und häufigen Fehler bei der Anwendung der Faktorenanalyse?
Die Faktorenanalyse trifft keine Aussagen über die Dimensionalität der Items.
Die klassische Variante der Faktorenanalyse beruht auf der Berechnung von Pearson Korrelationen bzw. Kovarianzen.
Demnach sollten die für eine Faktorenanalyse herangezogenen Items metrisch sein.
Weiters sind die Ergebnisse (vor allem die Anzahl an Faktoren) stark stichprobenabhängig.
Je homogener die Stichprobe, desto geringer die Korrelationen zwischen den Items und umso mehr Faktoren ergeben sich. Demnach müssten z.B. die Gewichtungen für die gewichteten Summen in jeder Stichprobe neu berechnet werden.
Für den Fall dichotomer Items sollte als Basis für die faktorenanalytischen Berechnungen die tetrachorische Korrelation herangezogen werden. Die Höhe der Vierfelderkorrelation (=Pearson Korrelation für zwei dichotome Items) hängt stark von den Itemschwierigkeiten der Items ab und führt somit zu artifiziellen Ergebnissen. Die Faktoren bilden zumeist Gruppen von in etwa gleich schweren Items.
Mitunter bilden die Faktoren nur das Antwortwortverhalten der Personen ab. So können z.B. Fragen, die von Personen meist bejaht werden, in einem gemeinsamen Faktor hoch laden auch wenn damit inhaltlich völlig unterschiedliche „Dimensionen“ abgefragt wurden.
Die klassische Variante der Faktorenanalyse beruht auf der Berechnung von Pearson Korrelationen bzw. Kovarianzen.
Demnach sollten die für eine Faktorenanalyse herangezogenen Items metrisch sein.
Weiters sind die Ergebnisse (vor allem die Anzahl an Faktoren) stark stichprobenabhängig.
Je homogener die Stichprobe, desto geringer die Korrelationen zwischen den Items und umso mehr Faktoren ergeben sich. Demnach müssten z.B. die Gewichtungen für die gewichteten Summen in jeder Stichprobe neu berechnet werden.
Für den Fall dichotomer Items sollte als Basis für die faktorenanalytischen Berechnungen die tetrachorische Korrelation herangezogen werden. Die Höhe der Vierfelderkorrelation (=Pearson Korrelation für zwei dichotome Items) hängt stark von den Itemschwierigkeiten der Items ab und führt somit zu artifiziellen Ergebnissen. Die Faktoren bilden zumeist Gruppen von in etwa gleich schweren Items.
Mitunter bilden die Faktoren nur das Antwortwortverhalten der Personen ab. So können z.B. Fragen, die von Personen meist bejaht werden, in einem gemeinsamen Faktor hoch laden auch wenn damit inhaltlich völlig unterschiedliche „Dimensionen“ abgefragt wurden.
Tags: Faktorenanalyse
Quelle: F202
Quelle: F202
Wie bzw. mit welchen Kennwerten erfolgt die Itemanalyse der klassischen Testtheorie?
Nach der Planung und Entwicklung der Items eines Tests müssen diese einer für den zukünftigen Anwendungsbereich des Tests möglichst repräsentativen Stichprobe vorgelegt werden, um die Eignung der Items deskriptivstatistisch (und eventuell faktorenanalytisch) zu untersuchen.
Die üblicherweise berechneten Kennwerte sind
Die Auswahl für den Test geeigneter Items basiert u.a. auf der gleichzeitigen Berücksichtigung der ermittelten Testkennwerte.
Selbstverständlich können auch die Ergebnisse der Faktorenanalyse zur Itemselektion herangezogen werden.
Die üblicherweise berechneten Kennwerte sind
- Itemschwierigkeit - Zahl zwischen 0 und 1- Eher Itemleichtigkeit – da: je näher als 1 desto leichter.- Bei Items die dichotom messen ist dies (mal 100) der Prozentsatz der Personen die die Aufgabe lösen.
- Itemvarianz - Wie unterschiedlich sind die Ergebnisse?- Ist ein Hinweis, wie gut das Item es erlaubt unterschiedliche Personen auseinanderzuhalten.
- Itemtrennschärfe - Korrelation der Items mit der Gesamtpunkteanzahl- Anders gesagt: Misst dieses Item das gleiche wie die anderen Items im Test.
Die Auswahl für den Test geeigneter Items basiert u.a. auf der gleichzeitigen Berücksichtigung der ermittelten Testkennwerte.
Selbstverständlich können auch die Ergebnisse der Faktorenanalyse zur Itemselektion herangezogen werden.
Tags: Itemanalyse, Itemkonstruktion, Klassische Testtheorie
Quelle: F205
Quelle: F205
Was ist die Itemschwierigkeit? Wie wird diese berechnet?
Der Schwierigkeitsindex Pi eines Items i ist der Quotient aus der bei diesem Item tatsächlich erreichten Punktesumme aller N Personen und der bei diesem Item von allen Personen maximal erreichbaren Punktesumme multipliziert mit 100.

- Zahl zwischen 0 und 1
- Eher Itemleichtigkeit – da: je näher als 1 desto leichter.
- Bei Items die dichotom messen ist dies (mal 100) der Prozentsatz der Personen die die Aufgabe lösen.


- Zahl zwischen 0 und 1
- Eher Itemleichtigkeit – da: je näher als 1 desto leichter.
- Bei Items die dichotom messen ist dies (mal 100) der Prozentsatz der Personen die die Aufgabe lösen.

Tags: Itemanalyse, Itemschwierigkeit, Klassische Testtheorie
Quelle: F206
Quelle: F206
Bei einem Item können Personen zwischen 0 und 5 Punkte erzielen. Das Item wurde 120 Personen vorgelegt, die insgesamt 442 Punkte erzielten.
Wie schwierig ist das Item?
Wie schwierig ist das Item?

Tags: Itemanalyse, Itemschwierigkeit, Klassische Testtheorie
Quelle: F207
Quelle: F207
Bei einem Item können Personen zwischen 1 und 10 Punkte vergeben. Das Item wurde 150 Personen vorgelegt, die insgesamt 956 Punkte vergaben.
Wie „schwierig“ ist das Item?
Wie „schwierig“ ist das Item?

Tags: Itemanalyse, Itemschwierigkeit, Klassische Testtheorie
Quelle: F208
Quelle: F208
Ein dichotomes Item wurde 152 Personen vorgelegt und von 28 gelöst.
Wie schwierig ist das Item?
Wie schwierig ist das Item?

Zahl zwischen 0 und 1
Bei Items die dichotom messen ist dies (mal 100) der Prozentsatz der Personen die die Aufgabe lösen.
Tags: Itemanalyse, Itemschwierigkeit, Klassische Testtheorie
Quelle: F209
Quelle: F209
Was ist bzw. wie berechnet man die Itemvarianz?
Die Varianz der Items wird mittels der aus der Statistik bekannten Formeln für die Varianz ermittelt.

Vereinfacht gilt: je größer die Varianz eines Items, umso besser seine Fähigkeit zur Differenzierung (=Diskriminationsfähigkeit).

Vereinfacht gilt: je größer die Varianz eines Items, umso besser seine Fähigkeit zur Differenzierung (=Diskriminationsfähigkeit).
Tags: Itemanalyse, Itemvarianz, Klassische Testtheorie
Quelle: F210
Quelle: F210
Was versteht man unter der Itemtrennschärfe?
- Korrelation der Items mit der Gesamtpunkteanzahl
- Anders gesagt: Misst dieses Item das gleiche wie die anderen Items im Test.
Die Trennschärfe ri,t eines Item i ist der korrelative Zusammenhang zwischen den Punkten, die von einer Person v im Item i und den Punkten die von Person v im Gesamttest erzielt werden.

Neben der unkorrigierten Itemtrennschärfe gibt es auch noch
die korrigierte Itemtrennschärfe bei der die Punkteanzahl, die
eine Person im Gesamttest erzielt hat, um die Punktezahl die
im jeweiligen Item erzielt wurde reduziert wird.


- Anders gesagt: Misst dieses Item das gleiche wie die anderen Items im Test.
Die Trennschärfe ri,t eines Item i ist der korrelative Zusammenhang zwischen den Punkten, die von einer Person v im Item i und den Punkten die von Person v im Gesamttest erzielt werden.

Neben der unkorrigierten Itemtrennschärfe gibt es auch noch
die korrigierte Itemtrennschärfe bei der die Punkteanzahl, die
eine Person im Gesamttest erzielt hat, um die Punktezahl die
im jeweiligen Item erzielt wurde reduziert wird.


Tags: Itemanalyse, Itemtrennschärfe, Klassische Testtheorie
Quelle: F211
Quelle: F211
Tags: Itemanalyse, Itemtrennschärfe, Klassische Testtheorie
Quelle: F213
Quelle: F213
Welche Rolle spielt die Itemtrennschärfe bei der Validität eines Tests?
Die Validität eines Tests hängt davon ab wie valide die einzelnen Items sind, aber auch von der Itemtrennschärfe. – siehe Verdünnungsformel.
Also wenn alle Items exakt die gleiche Eigenschaft messen ist dies nicht besser sondern verschlechtert die Validität. D.h. das Messen einer einzelnen Eigenschaft ist nicht sinnvoll für Vorhersagen.
Es wurde ein Quotient entwickelt, der einem hilft einen Test (für eine Skala) zu verkürzen, aber dabei die Validität möglichst hoch zu halten.
Die Validität kann man mit Hilfe der Faktorenanalyse erhalten: die Ladung (Konstruktvalidität)
Verdünnungsparadoxon
Eine interessante Erkenntnis bringt die Berechnung des Zusammenhangs von Itemtrennschärfe, Itemvalidität und der Validität des Gesamttests.

Zwar steigt die Validität eines Tests, wenn die einzelnen Items valider sind, jedoch nimmt die Testvalidität mit höher werdender Itemtrennschärfe ab.
Demnach sollte die Itemtrennschärfe eines Items nicht hoch sein.
Liegt pro Item sowohl eine Schätzung der Itemvalidität als auch die Itemtrennschärfe vor, kann der Quotient (Qi) aus den beiden als Kriterium dafür verwendet werden, welche Items bei einer geplanten Testverkürzung aus einem Test entfernt werden können, um die Testvalidität trotzdem größt möglich zu halten.

Es wird die gewünschte Anzahl von Items mit den geringsten Quotienten entfernt.
Also wenn alle Items exakt die gleiche Eigenschaft messen ist dies nicht besser sondern verschlechtert die Validität. D.h. das Messen einer einzelnen Eigenschaft ist nicht sinnvoll für Vorhersagen.
Es wurde ein Quotient entwickelt, der einem hilft einen Test (für eine Skala) zu verkürzen, aber dabei die Validität möglichst hoch zu halten.
Die Validität kann man mit Hilfe der Faktorenanalyse erhalten: die Ladung (Konstruktvalidität)
Verdünnungsparadoxon
Eine interessante Erkenntnis bringt die Berechnung des Zusammenhangs von Itemtrennschärfe, Itemvalidität und der Validität des Gesamttests.

Zwar steigt die Validität eines Tests, wenn die einzelnen Items valider sind, jedoch nimmt die Testvalidität mit höher werdender Itemtrennschärfe ab.
Demnach sollte die Itemtrennschärfe eines Items nicht hoch sein.
Liegt pro Item sowohl eine Schätzung der Itemvalidität als auch die Itemtrennschärfe vor, kann der Quotient (Qi) aus den beiden als Kriterium dafür verwendet werden, welche Items bei einer geplanten Testverkürzung aus einem Test entfernt werden können, um die Testvalidität trotzdem größt möglich zu halten.

Es wird die gewünschte Anzahl von Items mit den geringsten Quotienten entfernt.
Tags: Itemtrennschärfe, Validität, Verdünnungsformel
Quelle: F220
Quelle: F220
Was ist das Verdünnungsparadoxon?
Eine interessante Erkenntnis bringt die Berechnung des Zusammenhangs von Itemtrennschärfe, Itemvalidität und der Validität des Gesamttests.
Zwar steigt die Validität eines Tests, wenn die einzelnen Items valider sind, jedoch nimmt die Testvalidität mit höher werdender Itemtrennschärfe ab.
Demnach sollte die Itemtrennschärfe eines Items nicht hoch sein.

Liegt pro Item sowohl eine Schätzung der Itemvalidität als auch die Itemtrennschärfe vor, kann der Quotient (Qi) aus den beiden als Kriterium dafür verwendet werden, welche Items bei einer geplanten Testverkürzung aus einem Test entfernt werden können, um die Testvalidität trotzdem größt möglich zu halten.

Es wird die gewünschte Anzahl von Items mit den geringsten Quotienten entfernt.
Zwar steigt die Validität eines Tests, wenn die einzelnen Items valider sind, jedoch nimmt die Testvalidität mit höher werdender Itemtrennschärfe ab.
Demnach sollte die Itemtrennschärfe eines Items nicht hoch sein.

Liegt pro Item sowohl eine Schätzung der Itemvalidität als auch die Itemtrennschärfe vor, kann der Quotient (Qi) aus den beiden als Kriterium dafür verwendet werden, welche Items bei einer geplanten Testverkürzung aus einem Test entfernt werden können, um die Testvalidität trotzdem größt möglich zu halten.

Es wird die gewünschte Anzahl von Items mit den geringsten Quotienten entfernt.
Tags: Itemanalyse, Verdünnungsformel
Quelle: F220
Quelle: F220
Ich möchte aus den 5 Items 4 auswählen, sodass Validität des Test möglichst hoch bleibt:



(Verdünnungsparadoxon - Folie 221)
Formel nicht in Formelsammlung.
Was ist die Kritik an der klassischen Testtheorie?
Obwohl sich Tests, die nach der klassischen Testtheorie konstruiert wurden, in der Praxis durchaus bewährt haben, gibt es zahlreiche Kritikpunkte.
- Die Grundannahmen (Axiome) können nicht überprüft werden. Z.B. Korrelation der Parameter
- Das Intervallskalenniveau der Testergebnisse wird vorausgesetzt, kann jedoch nicht generell bewiesen werden. Problem mit rangskalierten Werten – man benötigt intervallskalierte Items, da man mit Varianzen, etc. arbeitet
- Alle im Rahmen der klassischen Testtheorie gewonnenen Kennwerte sind stichprobenabhängig. D.h. die Werte sind nicht verallgemeinerbar.
- Die Fairness der Summenbildung über verschiedene Items zur Ermittlung eines Gesamttestwerts ist nicht gesichert. Beispiel: 20 dichotome Items. Alle Personen die 3 Items richtig haben, sind alle gleich gut. Es ist aber unklar ob eine Person die schwierigeren Aufgaben gelöst hat, oder nicht. - Dies kann mit der modernen Testtheorie mathematisch bewiesen werden.
Tags: Klassische Testtheorie, Kritik
Quelle: F224
Quelle: F224
Welchen Einfluss hat die Stichprobe bei der klassischen Testtheorie auf folgende Kennwerte:
- Itemschwierigkeit
- Itemvarianz
- Reliabilität
- Validität
- Itemschwierigkeit
- Itemvarianz
- Reliabilität
- Validität
Itemschwierigkeit
Je besser die Stichprobe an der die Schwierigkeit eines Items erhoben wird, desto leichter erscheint das Item. Aber auch der Vergleich des Schwierigkeitsverhältnisses zweier Items hängt von der Stichprobe ab.

Itemvarianz
Die größte Varianz kann bei mittelschweren Items erzielt werden. Je schwerer (oder leichter) ein Item wird, umso geringer ist die Varianz aufgrund von Boden- und Deckeneffekten.
z.B. : Dichotome Items: Extrem leichte (immer gelöste) oder extrem schwere (nie gelöste) Items, haben eine Varianz von 0.
Reliabilität

Validität

Da wir gezeigt haben, dass die Reliabilität von der Stichprobe abhängt, hängt auch die Validität von der Stichprobe ab.
Je besser die Stichprobe an der die Schwierigkeit eines Items erhoben wird, desto leichter erscheint das Item. Aber auch der Vergleich des Schwierigkeitsverhältnisses zweier Items hängt von der Stichprobe ab.

Itemvarianz
Die größte Varianz kann bei mittelschweren Items erzielt werden. Je schwerer (oder leichter) ein Item wird, umso geringer ist die Varianz aufgrund von Boden- und Deckeneffekten.
z.B. : Dichotome Items: Extrem leichte (immer gelöste) oder extrem schwere (nie gelöste) Items, haben eine Varianz von 0.
Reliabilität

Validität

Da wir gezeigt haben, dass die Reliabilität von der Stichprobe abhängt, hängt auch die Validität von der Stichprobe ab.
Tags: Itemschwierigkeit, Itemvarianz, Klassische Testtheorie, Reliabilität, Validität
Quelle: F225
Quelle: F225
Kann die Item Response Theory auch für Persönlichkeitsfragebögen eingesetzt werden?
JA
Itemschwierigkeit und Personenfähigkeit sind ganz klar assoziiert mit Leistungstests. Die IRT ist aber auch für die Analyse von Items zur Erfassung von Persönlichkeitsmerkmalen möglich (hier würde man die Personenfähigkeit als Ausprägung bezeichnen).
Obwohl in weiterer Folge aus Gründen der besseren Verständlichkeit angenommen wird, dass das zu messende Merkmal eine Fähigkeit ist und daher auch von der Personenfähigkeit und der „Lösungswahrscheinlichkeit“ eines Items gesprochen wird, ist die Item Response Theory (IRT) prinzipiell auch für die Analyse von Items zur Erfassung von Persönlichkeitsmerkmalen und Einstellungen geeignet.
Itemschwierigkeit und Personenfähigkeit sind ganz klar assoziiert mit Leistungstests. Die IRT ist aber auch für die Analyse von Items zur Erfassung von Persönlichkeitsmerkmalen möglich (hier würde man die Personenfähigkeit als Ausprägung bezeichnen).
Obwohl in weiterer Folge aus Gründen der besseren Verständlichkeit angenommen wird, dass das zu messende Merkmal eine Fähigkeit ist und daher auch von der Personenfähigkeit und der „Lösungswahrscheinlichkeit“ eines Items gesprochen wird, ist die Item Response Theory (IRT) prinzipiell auch für die Analyse von Items zur Erfassung von Persönlichkeitsmerkmalen und Einstellungen geeignet.
Tags: IRT, Persönlichkeitsfragebogen
Quelle: F230
Quelle: F230
Was ist die Grundidee bzw. sind die Grundannahmen der Item Response Theory?
Im Gegensatz zur klassischen Testtheorie, die erst beim Testwert ansetzt, sich jedoch nicht näher damit beschäftigt, wie es zu dem Testergebnis kommt, setzen Modelle der IRT bereits an der Formulierung des Zusammenhangs von latenter Dimension und manifester Variable an.
Ähnlich wie bei der Faktorenanalyse geht es also darum, dass manifeste Antwortverhalten durch die individuellen Merkmalsausprägungen der Personen erklären zu können.
Im Allgemeinen wird davon ausgegangen, dass drei Komponenten die beobachtete Antwort (bzw. die Wahrscheinlichkeit für eine beobachtete Antwort) beeinflussen. Bei den drei Komponenten handelt es sich um
Weiters wird bei den meisten Modellen im Rahmen der IRT von der Existenz einer einzigen latenten Dimension ausgegangen. Die beobachteten Antworten der Person (oder auch die vorliegenden Symptome) werden als Indikatoren dieser latenten Dimension aufgefasst. Mit ihrer Hilfe lässt sich die Ausprägung der Person auf der latenten Dimension abschätzen.
Der Zusammenhang zwischen der Ausprägung auf der latenten Dimension und der Wahrscheinlichkeit für eine bestimmte Antwort wird durch die Itemcharakteristik hergestellt. Es handelt sich dabei um eine eindeutige aber nicht zwingend eindeutig umkehrbare Funktion.
Eine „technische“ Annahme ist die „lokal stochastische Unabhängigkeit“ der Items. Das bedeutet, dass davon ausgegangen wird, dass in einer Gruppe von Personen mit gleicher Personenfähigkeit, die Lösungswahrscheinlichkeit eines Items unabhängig davon ist, ob die Person das zuvor vorgegebene Item gelöst hat oder nicht.
Für die praktische Anwendung bedeutet das, dass die Lösungen von Aufgaben nicht aufeinander aufbauen dürfen bzw. die Reihenfolge in der die Items bearbeitet werden, keine Rolle spielen darf.
Ähnlich wie bei der Faktorenanalyse geht es also darum, dass manifeste Antwortverhalten durch die individuellen Merkmalsausprägungen der Personen erklären zu können.
Im Allgemeinen wird davon ausgegangen, dass drei Komponenten die beobachtete Antwort (bzw. die Wahrscheinlichkeit für eine beobachtete Antwort) beeinflussen. Bei den drei Komponenten handelt es sich um
- Eigenschaften der Person (z.B. Fähigkeit),
- Eigenschaften des Items (z.B. Schwierigkeit) und
- zufällige Einflüsse.
Weiters wird bei den meisten Modellen im Rahmen der IRT von der Existenz einer einzigen latenten Dimension ausgegangen. Die beobachteten Antworten der Person (oder auch die vorliegenden Symptome) werden als Indikatoren dieser latenten Dimension aufgefasst. Mit ihrer Hilfe lässt sich die Ausprägung der Person auf der latenten Dimension abschätzen.
Der Zusammenhang zwischen der Ausprägung auf der latenten Dimension und der Wahrscheinlichkeit für eine bestimmte Antwort wird durch die Itemcharakteristik hergestellt. Es handelt sich dabei um eine eindeutige aber nicht zwingend eindeutig umkehrbare Funktion.
Eine „technische“ Annahme ist die „lokal stochastische Unabhängigkeit“ der Items. Das bedeutet, dass davon ausgegangen wird, dass in einer Gruppe von Personen mit gleicher Personenfähigkeit, die Lösungswahrscheinlichkeit eines Items unabhängig davon ist, ob die Person das zuvor vorgegebene Item gelöst hat oder nicht.
Für die praktische Anwendung bedeutet das, dass die Lösungen von Aufgaben nicht aufeinander aufbauen dürfen bzw. die Reihenfolge in der die Items bearbeitet werden, keine Rolle spielen darf.
Tags: IRT, Itemcharakteristik
Quelle: F231
Quelle: F231
Was ist die Itemcharakteristik? Welche Arten können unterschieden werden?
Die verschiedenen im Rahmen der IRT definierten Modelle unterscheiden sich im Wesentlichen hinsichtlich des angenommenen Zusammenhangs zwischen der Ausprägung auf der latenten Dimension und der Wahrscheinlichkeit für eine bestimmte Antwort.
Dieser Zusammenhang wird durch die Itemcharakteristik hergestellt. Es handelt sich dabei um eine eindeutige aber nicht zwingend eindeutig umkehrbare Funktion.
Das bedeutet, dass z.B. jeder Personenfähigkeit eine eindeutige Lösungswahrscheinlichkeit für ein bestimmtes Item zugeordnet ist, es aber Personen mit unterschiedlicher Fähigkeit geben kann, die dieselbe Lösungswahrscheinlichkeit bei einem Item besitzen.
Die grafische Darstellung dieses Zusammenhangs nennt sich Itemcharakteristik Kurve (ICC).
Es werden drei Typen von Itemcharakteristiken unterschieden
Dieser Zusammenhang wird durch die Itemcharakteristik hergestellt. Es handelt sich dabei um eine eindeutige aber nicht zwingend eindeutig umkehrbare Funktion.
Das bedeutet, dass z.B. jeder Personenfähigkeit eine eindeutige Lösungswahrscheinlichkeit für ein bestimmtes Item zugeordnet ist, es aber Personen mit unterschiedlicher Fähigkeit geben kann, die dieselbe Lösungswahrscheinlichkeit bei einem Item besitzen.
Die grafische Darstellung dieses Zusammenhangs nennt sich Itemcharakteristik Kurve (ICC).
Es werden drei Typen von Itemcharakteristiken unterschieden
- streng monotone Funktionen Bei streng monotonen Funktionen nimmt die Lösungswahrscheinlichkeit eines Items mit zunehmender Ausprägung der Person in der latenten Dimension stetig zu oder ab.
- monotone Funktionen Bei monotonen Funktionen können „Plateaus“ auftreten, sodass Personen mit ähnlichen Fähigkeiten gleiche Lösungswahrscheinlichkeiten haben.
- nicht monotone Funktionen Nicht monotone Funktionen können sowohl steigen als auch fallen.



Tags: IRT, Itemcharakteristik
Quelle: F234
Quelle: F234
Was ist die Guttman-Skala?
Itemcharakteristik nach Guttman.
Guttman (1950) war der erste, der einen Zusammenhang zwischen Personenfähigkeit und Lösungswahrscheinlichkeit modellierte. Es handelt sich dabei um die sogenannte „Guttman Skala“ auch „Skalogramm Analyse“ genannt.
Bei der Itemcharakteristik der „Guttman Skala“ handelt es sich um eine Sprungfunktion, wobei die Itemlösungswahrscheinlichkeit nur die Ausprägungen 0 und 1 annehmen kann. So mit ist das Modell nicht probabilistisch sondern deterministisch.
Trotzdem lassen sich damit wesentliche Erkenntnisse über die IRT ableiten.

- X-Achse: Personenfähigkeit / Y-Achse: Lösungswahrscheinlichkeit
- Alle Personen die eine Personenfähigkeit von < -2 haben, kann keiner die Aufgabe lösen. Ab einer Personenfähigkeit von >-2 können alle, immer die Aufgabe lösen.
Man kann die Itemschwierigkeit bzw. Lösungswahrscheinlichkeit ablesen an der Skala der Personenfähigkeit.
D.h. man gibt die Lösungswahrscheinlichkeit in der Skala der Personenfähigkeit an – d.h. es liegt den beiden Skalen der gleiche Maßstab zu Grunde.
Guttman (1950) war der erste, der einen Zusammenhang zwischen Personenfähigkeit und Lösungswahrscheinlichkeit modellierte. Es handelt sich dabei um die sogenannte „Guttman Skala“ auch „Skalogramm Analyse“ genannt.
Bei der Itemcharakteristik der „Guttman Skala“ handelt es sich um eine Sprungfunktion, wobei die Itemlösungswahrscheinlichkeit nur die Ausprägungen 0 und 1 annehmen kann. So mit ist das Modell nicht probabilistisch sondern deterministisch.
Trotzdem lassen sich damit wesentliche Erkenntnisse über die IRT ableiten.

- X-Achse: Personenfähigkeit / Y-Achse: Lösungswahrscheinlichkeit
- Alle Personen die eine Personenfähigkeit von < -2 haben, kann keiner die Aufgabe lösen. Ab einer Personenfähigkeit von >-2 können alle, immer die Aufgabe lösen.
Man kann die Itemschwierigkeit bzw. Lösungswahrscheinlichkeit ablesen an der Skala der Personenfähigkeit.
D.h. man gibt die Lösungswahrscheinlichkeit in der Skala der Personenfähigkeit an – d.h. es liegt den beiden Skalen der gleiche Maßstab zu Grunde.
Tags: Guttman-Skala, IRT
Quelle: F241
Quelle: F241
- Welches ist die einfachste Aufgabe?
- Welches ist die schwerste Aufgabe?
- Wie ist die Lösungswahrscheinlichkeit einer Person mit dem Personenfähigkeitsparameter von 2 für die 3 Aufgaben?

- Welches ist die schwerste Aufgabe?
- Wie ist die Lösungswahrscheinlichkeit einer Person mit dem Personenfähigkeitsparameter von 2 für die 3 Aufgaben?

- Welches ist die einfachste Aufgabe? Schwarz
- Welches ist die schwerste Aufgabe? Grün
- Wie ist die Lösungswahrscheinlichkeit einer Person mit dem Personenfähigkeitsparameter von 2?
Schwarz = 1; rot = 1; grün = 0
- Welches ist die schwerste Aufgabe? Grün
- Wie ist die Lösungswahrscheinlichkeit einer Person mit dem Personenfähigkeitsparameter von 2?
Schwarz = 1; rot = 1; grün = 0
Tags: Guttman-Skala, IRT
Quelle: F242
Quelle: F242
Was illustriert die Guttman-Skala?
Die Guttman Skala illustriert, dass
- die Schwierigkeit des Items und die Personenfähigkeit anhand der selben Skala abgelesen werden kann. Bei der Guttman Skala markiert die Personenfähigkeit, die an der Sprungstelle liegt, die Schwierigkeit des Items,
- zur Modellierung der Lösungswahrscheinlichkeit aller Items nur eine Dimension angenommen wird und
- anhand des Modells Vorhersagen gemacht werden können, die anhand der manifesten Items überprüfbar sind. Bei der Guttman Skala handelt es sich dabei um die „erlaubten“ Antwortmuster.
Tags: Guttman-Skala, IRT
Quelle: F243
Quelle: F243
Was ist das "Latent Distance Model" von Lazarsfeld?
Da die Guttman Skala unrealistische Forderungen an die Items stellt, wurde der deterministische Ansatz von Lazarsfeld durch einen probabilistischen ersetzt.
Bei der Itemcharakteristik des „Latent Distance Models“ handelt es sich ebenfalls um eine Sprungfunktion, wobei pro Items zwei Itemlösungswahrscheinlichkeiten modelliert
werden. Diese beiden Lösungswahrscheinlichkeiten können bei jedem Item anders sein und müssen aus den Daten geschätzt werden.
Die Lösungswahrscheinlichkeiten sind jedoch nicht 0 und 1 ... sondern 0,13 und 0,86. Hier ist also die Ratewahrscheinlichkeit mitberücksichtigt, trotzdem das richtige anzukreuzen, obwohl man die Personenfähigkeit nicht hat.

Dadurch sind alle Antwortmuster möglich, treten jedoch mit
unterschiedlichen Wahrscheinlichkeiten auf.
Dieses Modell ist ein extrem parameterreiches Modell, da man 3 unbekannte Parameter hat (untere Lösungswahrscheinlichkeit, Sprungstelle und obere Lösungswahrscheinlichkeit).
Obwohl das „Latent Distance“ - Modell realistischere Anforderungen an die Items stellt als die Guttman Skala, ist
die Annahme von konstant bleibenden Itemlösungswahrscheinlichkeiten bei steigender Personenfähigkeit wenig realistisch.
Realistischer erscheint, dass die Lösungswahrscheinlichkeit mit steigender Personenfähigkeit zunimmt.
Aus diesem Grund wurde nach anderen, realistischeren Funktionen gesucht .... z.B. dichotom logistische Modell von Rasch.
Bei der Itemcharakteristik des „Latent Distance Models“ handelt es sich ebenfalls um eine Sprungfunktion, wobei pro Items zwei Itemlösungswahrscheinlichkeiten modelliert
werden. Diese beiden Lösungswahrscheinlichkeiten können bei jedem Item anders sein und müssen aus den Daten geschätzt werden.
Die Lösungswahrscheinlichkeiten sind jedoch nicht 0 und 1 ... sondern 0,13 und 0,86. Hier ist also die Ratewahrscheinlichkeit mitberücksichtigt, trotzdem das richtige anzukreuzen, obwohl man die Personenfähigkeit nicht hat.

Dadurch sind alle Antwortmuster möglich, treten jedoch mit
unterschiedlichen Wahrscheinlichkeiten auf.
Dieses Modell ist ein extrem parameterreiches Modell, da man 3 unbekannte Parameter hat (untere Lösungswahrscheinlichkeit, Sprungstelle und obere Lösungswahrscheinlichkeit).
Obwohl das „Latent Distance“ - Modell realistischere Anforderungen an die Items stellt als die Guttman Skala, ist
die Annahme von konstant bleibenden Itemlösungswahrscheinlichkeiten bei steigender Personenfähigkeit wenig realistisch.
Realistischer erscheint, dass die Lösungswahrscheinlichkeit mit steigender Personenfähigkeit zunimmt.
Aus diesem Grund wurde nach anderen, realistischeren Funktionen gesucht .... z.B. dichotom logistische Modell von Rasch.
Tags: IRT, Latent Distance Model
Quelle: F244
Quelle: F244
Was ist die leichteste, was ist die schwerste Aufgabe?


Bei Sprungfunktionen bleibt die Itemschwierigkeit gleich (d.h. die Sprungstelle definiert die Itemschwierigkeit): das schwarze Item ist das leichteste, das grüne ist das schwerste.
Es ist dabei egal wie groß der Sprung ist.
Es ist dabei egal wie groß der Sprung ist.
Tags: IRT, Latent Distance Model
Quelle: F245
Quelle: F245
Was entwickelte Georg Rasch (Allgemein)?
- Georg Rasch, dänischer Mathematiker
- Fischer (Uni Wien) hat dieses Modell entdeckt und hat es in die Psychologie eingeführt – dies begründete die methodischen Schwerpunkte der Uni Wien. (Forscherkreis um Fischer: Gittler, Kubinger,…)
Georg Rasch hat als Itemcharakteristik die logistische Funktion gewählt.
(U = Unbekannte)

Keine Sprungfunktion, sondern ein kontinuierlicher Wachstum der Wahrscheinlichkeit.
Egal welche Zahl für U eingesetzt wird – das Ergebnis ist immer ein Wert zwischen 0 und 1.
+ ∞ = 1
- ∞ = 0
Mit höherer Personenfähigkeit wird die Lösungswahrscheinlichkeit kontinuierlich höher. = Streng monotone Funktion

U wird von Rasch definiert als Personenfähigkeit (xi) minus der Itemschwierigkeit (sigma/
 ). (Achtung
). (Achtung  ist hier keine Standardabweichung).
ist hier keine Standardabweichung).Tags: IRT, Rasch-Modell
Quelle: F247
Quelle: F247
Wann steigt die Lösungswahrscheinlichkeit (nach dem Rasch-Modell)
a) wenn die Itemschwierigkeit gleich bleibt?
b) wenn die Personenfähigkeit gleich bleibt?
a) wenn die Itemschwierigkeit gleich bleibt?
b) wenn die Personenfähigkeit gleich bleibt?
a) Wenn die Personenfähigkeit steigt (bei gleichbleibender Itemschwierigkeit).
b) Wenn die Itemschwierigkeit sinkt (bei gleichbleibender Personenfähigkeit).

b) Wenn die Itemschwierigkeit sinkt (bei gleichbleibender Personenfähigkeit).

Tags: IRT, Rasch-Modell
Quelle: F252
Quelle: F252
Erkläre diese Formel und was bedingt diese Formel


Der Parameter U soll nun mit den für das Modell wesentlichen
Kennwerten (der Personenfähigkeit und der Itemschwierigkeit) in
Verbindung gebracht werden.

Somit ist die Itemcharakteristik gegeben durch

Demnach haben Personen bei Items, deren Schwierigkeit der Personenfähigkeit entsprechen, eine Lösungswahrscheinlichkeit von p(+|v,i) = 0.5. Ist die Personenfähigkeit geringer als das Item schwierig ist p(+|v,i) < 0.5. Ist die Person fähiger als das Item schwierig, ist p(+|v,i) > 0.5.
Kennwerten (der Personenfähigkeit und der Itemschwierigkeit) in
Verbindung gebracht werden.

Somit ist die Itemcharakteristik gegeben durch

Demnach haben Personen bei Items, deren Schwierigkeit der Personenfähigkeit entsprechen, eine Lösungswahrscheinlichkeit von p(+|v,i) = 0.5. Ist die Personenfähigkeit geringer als das Item schwierig ist p(+|v,i) < 0.5. Ist die Person fähiger als das Item schwierig, ist p(+|v,i) > 0.5.
Tags: IRT, Rasch-Modell
Quelle: F249
Quelle: F249
WIe groß ist die Lösungswahrscheinlichkeit lt. Rasch-Modell wenn die Person gleich fähig wie die Aufgabe schwer ist?
Personen haben bei Items, deren Schwierigkeit der Personenfähigkeit entsprechen, eine Lösungswahrscheinlichkeit von p(+|v,i) = 0.5. Ist die Personenfähigkeit geringer als das Item schwierig ist p(+|v,i) < 0.5. Ist die Person fähiger als das Item schwierig, ist p(+|v,i) > 0.5.

1 / 1+1 = 0,5 (d.h. die Lösungswahrscheinlichkeit liegt bei 50%)


1 / 1+1 = 0,5 (d.h. die Lösungswahrscheinlichkeit liegt bei 50%)

Tags: IRT, Rasch-Modell
Quelle: F250
Quelle: F250
Was definiert die Schwierigkeit des Items (Itemschwierigkeit)
a) beim Modell von Guttman?
b) beim Rasch-Modell?
a) beim Modell von Guttman?
b) beim Rasch-Modell?
a) Die Sprungstelle markiert die Schwierigkeit des Items.
b) Wenn die Person gleich fähig ist wie das Item schwierig: die Lösungswahrscheinlichkeit liegt bei 50%.
In der Graphik (schwarze Linie) – Itemschwierigkeit 0 (= Personenfähigkeit 0) (da beide Werte mit dem gleichen Maß gemessen werden)

Was ist das leichteste Item? Grün.
b) Wenn die Person gleich fähig ist wie das Item schwierig: die Lösungswahrscheinlichkeit liegt bei 50%.
In der Graphik (schwarze Linie) – Itemschwierigkeit 0 (= Personenfähigkeit 0) (da beide Werte mit dem gleichen Maß gemessen werden)

Was ist das leichteste Item? Grün.
Tags: Guttman-Skala, IRT, Itemschwierigkeit, Rasch-Modell
Quelle: F251
Quelle: F251
Was ist ein dichotomes Item im Sinne des Rasch-Modells?
a) Was ist die Hauptstadt Italiens?
b) Fragestellungen bei der Millionenshow?
c) MC-Klausuren mit Teilpunkte?
d) MC-Klausuren ohne Teilpunkte?
a) Was ist die Hauptstadt Italiens?
b) Fragestellungen bei der Millionenshow?
c) MC-Klausuren mit Teilpunkte?
d) MC-Klausuren ohne Teilpunkte?
a) Hauptstadt Italiens?
JA – weil entweder ist die Antwort richtig oder falsch (man bewertet nicht ob etwas „richtiger“ ist, z.B. Florenz ist nicht richtiger als Paris).
b) Sind die Fragen in der Millionenshow dichotome Items?
JA – denn es hat nichts mit der Anzahl der Antwortalternativen zu tun – sondern nur damit ob die Antwort richtig oder falsch.
c) MC-Klausuren mit Teilpunkten?
NEIN, da Fragen auch als teilweise richtig anerkannt werden.
d)MC-Klausuren ohne Teilpunkte?
JA, weil die Antwort auf diese Frage nur richtig oder falsch sein kann.
Dichotomes Item != Zwei Antwortalternativen (= dichotomes Antwortformat)!!
Dadurch ist es der Fall, dass die Lösungswahrscheinlichkeit bei einem dichotomen Item nicht zwangsläufig 50% ist.
JA – weil entweder ist die Antwort richtig oder falsch (man bewertet nicht ob etwas „richtiger“ ist, z.B. Florenz ist nicht richtiger als Paris).
b) Sind die Fragen in der Millionenshow dichotome Items?
JA – denn es hat nichts mit der Anzahl der Antwortalternativen zu tun – sondern nur damit ob die Antwort richtig oder falsch.
c) MC-Klausuren mit Teilpunkten?
NEIN, da Fragen auch als teilweise richtig anerkannt werden.
d)MC-Klausuren ohne Teilpunkte?
JA, weil die Antwort auf diese Frage nur richtig oder falsch sein kann.
Dichotomes Item != Zwei Antwortalternativen (= dichotomes Antwortformat)!!
Dadurch ist es der Fall, dass die Lösungswahrscheinlichkeit bei einem dichotomen Item nicht zwangsläufig 50% ist.
Tags: IRT, Rasch-Modell
Quelle: Mitschrift VO09
Quelle: Mitschrift VO09
Wie sieht die Formel aus für die Wahrscheinlichkeit, dass eine Person v ein Item i nicht löst?
Die Wahrscheinlichkeit, dass eine Person v das Item i nicht
löst ist gegeben durch

Die Kurve der Wahrscheinlichkeit ein Item zu Lösen und ein Item nicht zu lösen, verlaufen gegenläufig.

löst ist gegeben durch

Die Kurve der Wahrscheinlichkeit ein Item zu Lösen und ein Item nicht zu lösen, verlaufen gegenläufig.

Tags: IRT, Rasch-Modell
Quelle: F253
Quelle: F253
Was bedeutet dieser Formel:


Dies eine weitere Art der Modelldarstellung des dichotom logistischen Modells von Rasch:


Tags: IRT, Rasch-Modell
Quelle: F256
Quelle: F256
Welche Forderungen hatte Rasch an sein Modell?
Diese vier Forderungen umfassen also die Forderung nach
Achtung: Spezifische Objektivität von Vergleichen != Testgütekriterium Objektivität
Diese Eigenschaften können mathematisch bewiesen werden.

- spezifischer Objektivität von Vergleichen (Punkt 1, 2) und
- erschöpfenden (suffizienten) Statistiken (Punkt 3, 4).
Achtung: Spezifische Objektivität von Vergleichen != Testgütekriterium Objektivität
- Das Verhältnis der Schwierigkeiten zweier Items soll unabhängig von der gewählten Stichprobe sein. Wenn 2 Items die gleiche Eigenschaft messen, dann muss der Unterschied der Schwierigkeit im Verhältnis bei den Populationen gleich sein
- Das Verhältnis der Fähigkeiten zweier Personen soll unabhängig davon sein, welche Aufgaben den Personen zur Ermittlung der Personenfähigkeiten vorgegeben wurden. Wenn Items die gleiche Eigenschaft erfassen, dann muss unabhängig davon welche Items welcher Population vorgegeben werden, muss das Verhältnis der Fähigkeit gleich bleiben.(Anlehnung: 10 Kilo sind schwerer als 5 Kilo, unabhängig davon wer das Gewicht hebt.)
- Die Anzahl der gelösten Aufgaben soll die gesamte Information der Daten über die Fähigkeit der Person beinhalten. Wenn Personen den gleichen Test erhalten und gleich viele Punkte erhalten, dann kann man sagen „Die Personen sind gleich fähig.“
- Die Anzahl an Personen, die ein Item lösen können, soll die gesamte Information der Daten über die Schwierigkeit des Items beinhalten. Es darf für die Itemschwierigkeit nicht von Bedeutung sein, welche Person welches Item gelöst hat. Es ist nur noch relevant wie viele Items eine Person löst und wie viele Items insgesamt gelöst wurden.
Diese Eigenschaften können mathematisch bewiesen werden.

Tags: IRT, Rasch-Modell
Quelle: F257
Quelle: F257
Wie sollen die Itemcharakteristik-Kurven beim Rasch-Modell aussehen (folgend der Forderung nach spezifischer Objektivität)?
Aus der Forderung nach spezifischer Objektivität folgt, dass sich die IC Kurven nicht schneiden dürfen. Die IC Kurven müssen im Modell von Rasch also dieselbe Steigung (=Diskrimination) haben.

Dadurch, dass sie sich nie schneiden dürfen, müssen die Itemcharakteristikkurven parallel sein.

Dadurch, dass sie sich nie schneiden dürfen, müssen die Itemcharakteristikkurven parallel sein.
Tags: IRT, Itemcharakteristik, Rasch-Modell
Quelle: F260
Quelle: F260
Was versteht man unter Diskriminationfähigkeit einer Itemcharakteristik-Kurve?
Diskriminationsfähigkeit: Ist die Eigenschaft, wie schnell die Itemcharakteristikkurve ansteigt.

Rasch fordert also Items mit der gleichen Diskriminationsfähigkeit.
- Je flacher der Anstieg eines Items ist, desto geringer ist die Diskriminationsfähigkeit
- Gutmans-Sprungfunktion hat eine 100%ige Diskriminationsfähigkeit.

Rasch fordert also Items mit der gleichen Diskriminationsfähigkeit.
Tags: Diskriminationsfähigkeit, IRT, Itemcharakteristik, Rasch-Modell
Quelle: F260
Quelle: F260
Wie kann die Existenz der erschöpfenden Statistik für das Rasch-Modell gezeigt/bewiesen werden?
Die Existenz der erschöpfenden Statistiken kann anhand der Likelihood der Daten gezeigt werden.
Die Likelihood der Daten ist die Wahrscheinlichkeit, EXAKT die erhobenen Daten zu erhalten.
Likelihood ist nur noch von den Randsummen (Anzahl der gelösten Items einer Person und Anzahl wie oft ein Item gelöst wurdE) abhängig und nicht von den konkreten Antworten einer Person.
Die Likelihood der Daten ist die Wahrscheinlichkeit, EXAKT die erhobenen Daten zu erhalten.
Likelihood ist nur noch von den Randsummen (Anzahl der gelösten Items einer Person und Anzahl wie oft ein Item gelöst wurdE) abhängig und nicht von den konkreten Antworten einer Person.
Tags: Existenz der erschöpfenden Statistik, IRT, Likelihood, Rasch-Modell
Quelle: F261
Quelle: F261
Wie ist die Vorgehensweise beim Likelihood um die Existenz der erschöpfenden Statistik zu zeigen?
Die Existenz der erschöpfenden Statistiken kann anhand der Likelihood der Daten gezeigt werden. Die Likelihood der Daten ist die Wahrscheinlichkeit, EXAKT die erhobenen Daten zu erhalten.
Wie sehen diese Daten im Modell von Rasch aus?

Tabelle: Person 1 hat Item 1 falsch beantwortet (0) und Item 2 richtig beantwortet (1), etc.
Gehen wir nun davon aus, wir können die Antwort, die eine
Person v auf ein Item i gegeben hat, in eine
Wahrscheinlichkeit umwandeln, mit der Person v die
gegebene Antwort auf Item i gibt. Dadurch erhalten wir:

Jetzt muss für jede Person und Item berechnet werden wie wahrscheinlich es ist, dass diese Person genau dieses Item löst/nicht löst = Antwortmuster einer Person
Geht man weiters davon aus, dass die Wahrscheinlichkeit der
Lösung von Item i durch Person v unabhängig davon ist,
welche und wie viele Items Person v zuvor gelöst hat (=lokal
stochastische Unabhängigkeit), so kann die
Wahrscheinlichkeit, dass Person v ihr Antwortmuster zeigt,
berechnet werde durch:

(nicht stochastische Unabhängigkeit wenn aufeinander aufbauende Aufgaben oder eine Person lernt zwischen den Aufgaben (z.B. durch Rückmeldung über Ergebnis))
Geht man nun noch davon aus, dass die von den Personen
erzielten Antwortmuster unabhängig sind, so ist die
Wahrscheinlichkeit die gegebenen Daten zu erhalten
(=Likelihood der Daten) gegeben durch:

Sind die Daten voneinander unabhängig? Ja, wenn sie nicht voneinander abschauen (ev. auch problematisch bei mündl. Prüfungen, Partnerarbeiten, Online-Testungen, Person füllt Test mehrfach aus)
Je nach Variante muss die entsprechende Variante gewählt werden – entweder der 1. Term oder der 2. Term. Dies wird automatisch erreicht durch avj bzw. 1-avj …. Da bei richtigen Antworten mit 1 kodiert werden erhält man beim 1. Term bei einer richtigen Antwort den Term hoch 1 und dem 2. Term mit hoch 0 und so wird bei einer richtigen Antwort z.B. nur der 1. Term verwendet.
In der Formel kommt v und i nicht weiter vor – d.h. für die Berechnung der Wahrscheinlichkeit genau diese konkrete Daten zu erhalten (Likelihood) muss nicht die konkrete Antwort der Person gewusst werden = Beweis für die Existenz der erschöpfenden Statistik.

Wie sehen diese Daten im Modell von Rasch aus?

Tabelle: Person 1 hat Item 1 falsch beantwortet (0) und Item 2 richtig beantwortet (1), etc.
Gehen wir nun davon aus, wir können die Antwort, die eine
Person v auf ein Item i gegeben hat, in eine
Wahrscheinlichkeit umwandeln, mit der Person v die
gegebene Antwort auf Item i gibt. Dadurch erhalten wir:

Jetzt muss für jede Person und Item berechnet werden wie wahrscheinlich es ist, dass diese Person genau dieses Item löst/nicht löst = Antwortmuster einer Person
Geht man weiters davon aus, dass die Wahrscheinlichkeit der
Lösung von Item i durch Person v unabhängig davon ist,
welche und wie viele Items Person v zuvor gelöst hat (=lokal
stochastische Unabhängigkeit), so kann die
Wahrscheinlichkeit, dass Person v ihr Antwortmuster zeigt,
berechnet werde durch:

(nicht stochastische Unabhängigkeit wenn aufeinander aufbauende Aufgaben oder eine Person lernt zwischen den Aufgaben (z.B. durch Rückmeldung über Ergebnis))
Geht man nun noch davon aus, dass die von den Personen
erzielten Antwortmuster unabhängig sind, so ist die
Wahrscheinlichkeit die gegebenen Daten zu erhalten
(=Likelihood der Daten) gegeben durch:

Sind die Daten voneinander unabhängig? Ja, wenn sie nicht voneinander abschauen (ev. auch problematisch bei mündl. Prüfungen, Partnerarbeiten, Online-Testungen, Person füllt Test mehrfach aus)
Je nach Variante muss die entsprechende Variante gewählt werden – entweder der 1. Term oder der 2. Term. Dies wird automatisch erreicht durch avj bzw. 1-avj …. Da bei richtigen Antworten mit 1 kodiert werden erhält man beim 1. Term bei einer richtigen Antwort den Term hoch 1 und dem 2. Term mit hoch 0 und so wird bei einer richtigen Antwort z.B. nur der 1. Term verwendet.
In der Formel kommt v und i nicht weiter vor – d.h. für die Berechnung der Wahrscheinlichkeit genau diese konkrete Daten zu erhalten (Likelihood) muss nicht die konkrete Antwort der Person gewusst werden = Beweis für die Existenz der erschöpfenden Statistik.

Tags: Existenz der erschöpfenden Statistik, IRT, Likelihood, Rasch-Modell
Quelle: F261
Quelle: F261
Wie ergibt sich die Likelihood-Formel hinsichtlich der Berechnung der Lösungswahrscheinlichkeit für richtige und falsche Antworten?
(Anm: muss vermutlich nicht so im Detail gewusst werden)
Im dichotom logistischen Modell von Rasch können Personen zwei unterschiedliche Antworten geben.
Entweder sie antworten korrekt (1) oder nicht (0). Die Wahrscheinlichkeiten hierfür sind:

Je nach gegebener Antwort, muss die entsprechende Variante gewählt werden. Dies wird erreicht durch

Je nach Variante muss die entsprechende Variante gewählt werden – entweder der 1. Term oder der 2. Term. Dies wird automatisch erreicht durch avj bzw. 1-avj …. Da bei richtigen Antworten mit 1 kodiert werden erhält man beim 1. Term bei einer richtigen Antwort den Term hoch 1 und dem 2. Term mit hoch 0 und so wird bei einer richtigen Antwort z.B. nur der 1. Term verwendet.


Demnach wird allen Personen, die einem Test mit den selben Items dieselbe Anzahl gelöster Aufgaben erzielen, derselbe Fähigkeitsparameter zugeordnet.
Die Erkenntnis, dass die erschöpfenden Statistiken nur gelten, wenn die Items den Anforderungen des Modells von Rasch (RM) entsprechen, hat weitreichende Konsequenzen.
U.a. bedeutet es, dass die im Rahmen der klassischen Testtheorie vorgenommene Summenbildung zur Gewinnung eines Rohscores nur fair ist, wenn die Items dem RM entsprechen.
Im dichotom logistischen Modell von Rasch können Personen zwei unterschiedliche Antworten geben.
Entweder sie antworten korrekt (1) oder nicht (0). Die Wahrscheinlichkeiten hierfür sind:

Je nach gegebener Antwort, muss die entsprechende Variante gewählt werden. Dies wird erreicht durch

Je nach Variante muss die entsprechende Variante gewählt werden – entweder der 1. Term oder der 2. Term. Dies wird automatisch erreicht durch avj bzw. 1-avj …. Da bei richtigen Antworten mit 1 kodiert werden erhält man beim 1. Term bei einer richtigen Antwort den Term hoch 1 und dem 2. Term mit hoch 0 und so wird bei einer richtigen Antwort z.B. nur der 1. Term verwendet.


- Rohscore von Person v: Wieviele Items hat die Person gelöst?
- Absolute Lösungshäufigkeit von Item i: Wie oft wurde dieses Item gelöst?
- In der Formel kommt v und i nicht weiter vor – d.h. für die Berechnung der Wahrscheinlichkeit genau diese konkrete Antwort zu erhalten (Likelihood) muss nicht die konkrete Antwort der Person gewusst werden = Beweis für die Existenz der erschöpfenden Statistik.
Demnach wird allen Personen, die einem Test mit den selben Items dieselbe Anzahl gelöster Aufgaben erzielen, derselbe Fähigkeitsparameter zugeordnet.
Die Erkenntnis, dass die erschöpfenden Statistiken nur gelten, wenn die Items den Anforderungen des Modells von Rasch (RM) entsprechen, hat weitreichende Konsequenzen.
U.a. bedeutet es, dass die im Rahmen der klassischen Testtheorie vorgenommene Summenbildung zur Gewinnung eines Rohscores nur fair ist, wenn die Items dem RM entsprechen.
Tags: Existenz der erschöpfenden Statistik, IRT, Likelihood, Rasch-Modell
Quelle: F265
Quelle: F265
Was bedeutet es wenn die Existenz der erschöpfenden Statistik durch das Likelihood der Daten bewiesen wurde?

- Rohscore von Person v: Wieviele Items hat die Person gelöst?
- Absolute Lösungshäufigkeit von Item i: Wie oft wurde dieses Item gelöst?
- In der Formel kommt v und i nicht weiter vor – d.h. für die Berechnung der Wahrscheinlichkeit genau diese konkrete Antwort zu erhalten (Likelihood) muss nicht die konkrete Antwort der Person gewusst werden = Beweis für die Existenz der erschöpfenden Statistik.
Demnach wird allen Personen, die einem Test mit den selben Items dieselbe Anzahl gelöster Aufgaben erzielen, derselbe Fähigkeitsparameter zugeordnet.
Die Erkenntnis, dass die erschöpfenden Statistiken nur gelten, wenn die Items den Anforderungen des Modells von Rasch (RM) entsprechen, hat weitreichende Konsequenzen.
U.a. bedeutet es, dass die im Rahmen der klassischen Testtheorie vorgenommene Summenbildung zur Gewinnung eines Rohscores nur fair ist, wenn die Items dem RM entsprechen.
Die Existenz der erschöpfenden Statistik zeigt die Fairness des Rasch-Modells, d.h. es kommt nicht darauf an welche Items gelöst wurden, sondern nur wie viele Aufgaben gelöst wurden.
Tags: Existenz der erschöpfenden Statistik, Likelihood, Rasch-Modell
Quelle: F268
Quelle: F268
Was versteht man unter der spezifischen Objektivität?
Die spezifische Objektivität (also die Tatsache, dass z.B. das Verhältnis der Schwierigkeit zweier Items unabhängig von den getesteten Personen ist), kann anhand der nachfolgenden (bedingten) Wahrscheinlichkeit gezeigt werden:

Es ist die Wahrscheinlichkeit, dass Person v Item A löst und Item B nicht, vorausgesetzt Person v kann genau eines der beiden Items lösen.
In dieser Wahrscheinlichkeit steckt das Verhältnis der Itemschwierigkeiten (bzw. Itemleichtigkeiten).
Spezifische Objektivität: kann gezeigt werden durch die Betrachtung einer bedingten Wahrscheinlichkeit. Man möchte sich die Wahrscheinlichkeit berechnen, dass eine Person ein Item löst und das zweite Item nicht unter der Bedingung, dass sie nur ein Item lösen kann (man kann dies durch eine Vierfeldertafel darstellen). Dass heißt man lässt alle Personen außer Betracht die kein Item oder beide Items lösen können. Man lässt diese Personen weg, da diese Personen keine Aussage darüber liefern, welches Item schwieriger bzw. einfacher ist – d.h. die Personen sind nicht informativ.

Es ist die Wahrscheinlichkeit, dass Person v Item A löst und Item B nicht, vorausgesetzt Person v kann genau eines der beiden Items lösen.
In dieser Wahrscheinlichkeit steckt das Verhältnis der Itemschwierigkeiten (bzw. Itemleichtigkeiten).
Spezifische Objektivität: kann gezeigt werden durch die Betrachtung einer bedingten Wahrscheinlichkeit. Man möchte sich die Wahrscheinlichkeit berechnen, dass eine Person ein Item löst und das zweite Item nicht unter der Bedingung, dass sie nur ein Item lösen kann (man kann dies durch eine Vierfeldertafel darstellen). Dass heißt man lässt alle Personen außer Betracht die kein Item oder beide Items lösen können. Man lässt diese Personen weg, da diese Personen keine Aussage darüber liefern, welches Item schwieriger bzw. einfacher ist – d.h. die Personen sind nicht informativ.
Tags: spezifische Objektivität
Quelle: F270
Quelle: F270
Erkläre die Formel der spezifischen Objektivität:



Spezifische Objektivität: kann gezeigt werden durch die Betrachtung einer bedingten Wahrscheinlichkeit.
Man möchte sich die Wahrscheinlichkeit berechnen, dass eine Person ein Item löst und das zweite Item nicht unter der Bedingung, dass sie nur ein Item lösen kann (man kann dies durch eine Vierfeldertafel darstellen). Dass heißt man lässt alle Personen außer Betracht die kein Item oder beide Items lösen können. Man lässt diese Personen weg, da diese Personen keine Aussage darüber liefern, welches Item schwieriger bzw. einfacher ist – d.h. die Personen sind nicht informativ.
Formel der spezifischen Objektivität:
Nach der Umformung der Formel kann man θ_v herausheben und dann ergibt sich daraus das Schwierigkeitsverhältnis. D.h. die Schwierigkeit/Leichtigkeit eines Items ist unabhängig von der Personenfähigkeit.

Dies bedeutet auch, dass das Schwierigkeitsverhältnis zweier Items konstant bleibt.
Tags: spezifische Objektivität
Quelle: F271
Quelle: F271
Was ermöglicht die IRT dadurch, dass die Itemschwierigkeit unabhängig ist von der Personenfähigkeit?
Entspricht eine Menge von Items einem IRT Modell, so ermöglicht das Personen miteinander zu vergleichen, auch wenn sie nicht dieselben Aufgaben bearbeitet haben. Damit können die Tests an die Personen angepasst werden (=adaptives Testen).
Die beiden Arten des adaptiven Testens sind
Die beiden Arten des adaptiven Testens sind
- Tailored Testing (maßgeschneidertes Testen) und
- Branched Testing (verzweigtes Tests).
Tags: adaptiver Test, IRT
Quelle: F273
Quelle: F273
Welche Arten des adaptiven Testens können unterschieden werden?
Entspricht eine Menge von Items einem IRT Modell, so ermöglicht das Personen miteinander zu vergleichen, auch wenn sie nicht dieselben Aufgaben bearbeitet haben. Damit können die Tests an die Personen angepasst werden (=adaptives Testen).
Die beiden Arten des adaptiven Testens sind
Tailored Testing
Üblicherweise erhalten die Personen zu Beginn ein oder mehrere mittelschwere Items.
Beim tailored testing wird nach jeder Vorgabe eines Items der Personenparameter neu geschätzt und aus der Menge der vorhandenen Items (=Itempool) jenes Items ausgewählt, dessen Schwierigkeit der Personenfähigkeit am besten entspricht.
Diese Methode ist sehr rechenintensiv und erfordert eine computergestützte Testung.
Branched Testing
Aus diesem Grund werden beim branched testing bereits in der Testentwicklung Gruppen von Items zusammengestellt.
Je nachdem wie gut eine Person bei der ersten Itemgruppe abschneidet, wird eine weitere zuvor festgelegte Itemgruppe ausgewählt usw.

Die beiden Arten des adaptiven Testens sind
- Tailored Testing (maßgeschneidertes Testen) und
- Branched Testing (verzweigtes Tests).
Tailored Testing
Üblicherweise erhalten die Personen zu Beginn ein oder mehrere mittelschwere Items.
Beim tailored testing wird nach jeder Vorgabe eines Items der Personenparameter neu geschätzt und aus der Menge der vorhandenen Items (=Itempool) jenes Items ausgewählt, dessen Schwierigkeit der Personenfähigkeit am besten entspricht.
Diese Methode ist sehr rechenintensiv und erfordert eine computergestützte Testung.
Branched Testing
Aus diesem Grund werden beim branched testing bereits in der Testentwicklung Gruppen von Items zusammengestellt.
Je nachdem wie gut eine Person bei der ersten Itemgruppe abschneidet, wird eine weitere zuvor festgelegte Itemgruppe ausgewählt usw.

Tags: adaptive Testen
Quelle: F274
Quelle: F274
Wie können die Personen beim adaptiven Testen miteinander verglichen werden? Was sind die Vorteile des adaptiven Testens?
Die Vergleichbarkeit der Personen ist für den Fall, dass sie unterschiedliche Items bearbeiten jedoch nicht mehr über die Anzahl der gelösten Aufgaben, sondern nur noch über die geschätzte Personenparameter möglich.
Eine auf die Fähigkeiten der getesteten Personen abgestimmte Itemauswahl,
Bei der IRT darf man nicht mehr sagen: Personen die gleich viele Aufgaben gelöst haben sind gleich gut. Denn dies darf man nur sagen, wenn alle Personen die gleichen Items vorgelegt wurden.
Die Genauigkeit mit der wir eine Person messen können (Messfehler) hängt von der Vorgabe des Tests ab. Bei der klassischen Testtheorie geht man davon aus dass der Messfehler gleich groß ist. Bei der modernen Testtheorie kann man durch adaptives Testen den Messfehler reduzieren.
Eine auf die Fähigkeiten der getesteten Personen abgestimmte Itemauswahl,
- reduziert in vielen Fällen nicht nur die benötigte Testzeit und
- ermöglicht die Personen weitestgehend weder durch die Vorgabe von zu leichten Aufgaben zu „langweilen“ oder von zu schweren Aufgaben zu „demotivieren“, sondern
- erhöht auch die Genauigkeit der Schätzung des Personenparameters (Messfehler wird reduziert).
Bei der IRT darf man nicht mehr sagen: Personen die gleich viele Aufgaben gelöst haben sind gleich gut. Denn dies darf man nur sagen, wenn alle Personen die gleichen Items vorgelegt wurden.
Die Genauigkeit mit der wir eine Person messen können (Messfehler) hängt von der Vorgabe des Tests ab. Bei der klassischen Testtheorie geht man davon aus dass der Messfehler gleich groß ist. Bei der modernen Testtheorie kann man durch adaptives Testen den Messfehler reduzieren.
Tags: adaptives Testen, IRT
Quelle: F276
Quelle: F276
Wie kann die Parameterschätzung im Rasch-Modell erfolgen?
Die Schätzung der unbekannten Parameter erfolgt im Rasch Modell üblicherweise mit Hilfe der Maximum-Likelihood-Methode.
Hierbei werden die unbekannten Parameter so geschätzt, dass die Likelihood der Daten maximal wird.
Die Parameterschätzung benötigt man für die Schätzung der Personenfähigkeit bzw. der Itemschwierigkeit.


Hierbei werden die unbekannten Parameter so geschätzt, dass die Likelihood der Daten maximal wird.
Die Parameterschätzung benötigt man für die Schätzung der Personenfähigkeit bzw. der Itemschwierigkeit.


Tags: IRT, Maximum-Likelihood-Methode, Parameterschätzung, Rasch-Modell
Quelle: F277
Quelle: F277
Welche Arten der Maximum-Likelihood-Methode können unterschieden werden?
(für Parameterschätzung)
Es gibt der Arten der Maximum Likelihood Schätzungen
unbedingte Maximum Likelihood Methode (UML)
Die UML basiert auf der Totalen Likelihood der Daten.
Hierbei werden Personenfähigkeits- und Itemschwierigkeitsparameter gleichzeitig geschätzt. Bei dieser Methode muss für jedes Item aber auch für jede Person ein eigener Parameter geschätzt werden.
Das bedeutet jedoch, dass für jede neu hinzukommende Person ein weiterer Personenfähigkeitsparameter benötigt wird. Dies führt häufig zu gröberen Problemen bei der Schätzung.
bedingte Maximum Likelihood Methode (CML)
Bei der CML wird davon ausgegangen, dass pro Person die Zahl der gelösten Aufgaben bekannt ist. Somit werden die Personenparameter durch die Anzahl gelöster Aufgaben ersetzt und es müssen zunächst „nur“ die Itemschwierigkeitsparameter geschätzt werden.
Die Schätzung der Personenparameter erfolgt dann wiederum mittels der UML. Personen mit der gleichen Anzahl an gelösten Aufgaben wird der selbe Personenparameter zugeordnet. Allerdings kann für Personen, die alle oder kein Item gelöst haben, kein Fähigkeitsparameter geschätzt werden.
marginale Maximum Likelihood Methode (MML)
Auch bei der MML werden zunächst nur die Itemparameter geschätzt. Anstatt von pro Person bekannten Rohscores auszugehen, wird nur von einer bestimmten Verteilung der Personenparameter ausgegangen (z.B. NV). Somit müssen anstatt der einzelnen Personenparameter vorerst nur die Parameter der Verteilung (z.B. Mittelwert und Varianz) geschätzt werden.
Nach der Schätzung der Itemparameter werden die Personenparameter abermals mittels UML geschätzt. Verzerrungen ergeben sich, wenn die vorab angenommene Verteilung der Personenparameter falsch ist.
Es gibt der Arten der Maximum Likelihood Schätzungen
- die unbedingte Maximum Likelihood Methode (UML)
- die bedingte Maximum Likelihood Methode (CML) und
- die marginale Maximum Likelihood Methode (MML).
unbedingte Maximum Likelihood Methode (UML)
Die UML basiert auf der Totalen Likelihood der Daten.
Hierbei werden Personenfähigkeits- und Itemschwierigkeitsparameter gleichzeitig geschätzt. Bei dieser Methode muss für jedes Item aber auch für jede Person ein eigener Parameter geschätzt werden.
Das bedeutet jedoch, dass für jede neu hinzukommende Person ein weiterer Personenfähigkeitsparameter benötigt wird. Dies führt häufig zu gröberen Problemen bei der Schätzung.
- Muss sehr viele Parameter schätzen
- In der Praxis gibt es Schätzprobleme.
bedingte Maximum Likelihood Methode (CML)
Bei der CML wird davon ausgegangen, dass pro Person die Zahl der gelösten Aufgaben bekannt ist. Somit werden die Personenparameter durch die Anzahl gelöster Aufgaben ersetzt und es müssen zunächst „nur“ die Itemschwierigkeitsparameter geschätzt werden.
Die Schätzung der Personenparameter erfolgt dann wiederum mittels der UML. Personen mit der gleichen Anzahl an gelösten Aufgaben wird der selbe Personenparameter zugeordnet. Allerdings kann für Personen, die alle oder kein Item gelöst haben, kein Fähigkeitsparameter geschätzt werden.
- Nutzt die Information, dass sie weiß wieviele Personen ein Item gelöst haben und wieviele Aufgaben eine Person bereits gelöst hat.
- Durch das Erhöhen der Personenanzahl wird die Anzahl der zu schätzenden Personenfähigkeitsparameter gleich (Personen mit gleicher Rohscore wird derselbe Personenparameter zugeordnet).
marginale Maximum Likelihood Methode (MML)
Auch bei der MML werden zunächst nur die Itemparameter geschätzt. Anstatt von pro Person bekannten Rohscores auszugehen, wird nur von einer bestimmten Verteilung der Personenparameter ausgegangen (z.B. NV). Somit müssen anstatt der einzelnen Personenparameter vorerst nur die Parameter der Verteilung (z.B. Mittelwert und Varianz) geschätzt werden.
Nach der Schätzung der Itemparameter werden die Personenparameter abermals mittels UML geschätzt. Verzerrungen ergeben sich, wenn die vorab angenommene Verteilung der Personenparameter falsch ist.
- Geht von einer Verteilung der Personenfähigkeitsparameter aus. D.h. es wird der Mittelwert und die Streuung von Personenfähigkeitsparameter und Itemschwierigkeit geschätzt.
- Problem: wenn die Verteilung nicht passt erhält man falsche Daten.
- Man kriegt auch Personenparameter für Personen die alles gelöst haben und Personen die nichts gelöst haben (dies ist nicht der Fall bei der CML)
- (Parametermäßig am besten aber man benötigt zusätzliche Information zur Verteilung)
Tags: Maximum-Likelihood-Methode
Quelle: F280
Quelle: F280
Wann ergeben sich Probleme bei der Maximum-Likelihood-Methode? Wovon hängt die Genauigkeit der Schätzung ab?
Probleme bei der Parameterschätzung ergeben sich, wenn es kein eindeutig definiertes Maximum der Likelihoodfunktion gibt.
Dies ist der Fall, wenn die Funktion

Die Genauigkeit der Schätzung hängt davon ab, wie viel Information man über einen Parameter besitzt.
Die Genauigkeit der Parameterschätzung der Personenfähigkeit kann erhöht werden durch die zusätzliche Abfrage von Items mit einer Itemschwierigkeit die der aktuellen Personenfähigkeit entsprechen (da diese Items die Person mit einer Wahrscheinlichkeit von 50% löst).
Dies ist der Fall, wenn die Funktion
- multiple Maxima hat (d.h. es neben den globalen noch lokale Maxima gibt) oder
- das Maximum kein Punkt, sondern ein Plateau oder eine Fläche ist.

Die Genauigkeit der Schätzung hängt davon ab, wie viel Information man über einen Parameter besitzt.
Die Genauigkeit der Parameterschätzung der Personenfähigkeit kann erhöht werden durch die zusätzliche Abfrage von Items mit einer Itemschwierigkeit die der aktuellen Personenfähigkeit entsprechen (da diese Items die Person mit einer Wahrscheinlichkeit von 50% löst).
Tags: Maximum-Likelihood-Methode, Parameterschätzung
Quelle: F284
Quelle: F284
Was ist die Informationsfunktion?

Die Information = Die Wahrscheinlichkeit dass das Ereignis eintritt mal der Wahrscheinlichkeit dass das Ereignis nicht eintritt.

Je ähnlicher die Schwierigkeit eines Items i der Fähigkeit einer Person v ist, umso höher ist die Information, die eine Person über ein Item bzw. ein Item über eine Person liefert.
Die Genauigkeit der Parameterschätzung der Personenfähigkeit kann erhöht werden durch die zusätzliche Abfrage von Items mit einer Itemschwierigkeit die der aktuellen Personenfähigkeit entsprechen (da diese Items die Person mit einer Wahrscheinlichkeit von 50% löst).

Je größer die Information, die man über ein Item bzw. über eine Person sammelt, umso genauer kann man den Item bzw.
Personenparameter schätzen.
Daraus folgt:
Hat man einen fixen Test, so ist die Messgenauigkeit dieses Tests nicht bei allen Personen gleich.
Für die Items gilt: je stärker die Itemschwierigkeit von der durchschnittlichen Personenfähigkeit einer Gruppe abweicht umso ungenauer ist die Schätzung der Itemschwierigkeit.
Bei einem fixen Test ist die Messgenauigkeit nicht bei allen Personen gleich, denn je besser die Personenfähigkeit zur Itemschwierigkeit passt, desto besser kann man die Personenfähigkeit schätzen.

Je ähnlicher die Schwierigkeit eines Items i der Fähigkeit einer Person v ist, umso höher ist die Information, die eine Person über ein Item bzw. ein Item über eine Person liefert.
Die Genauigkeit der Parameterschätzung der Personenfähigkeit kann erhöht werden durch die zusätzliche Abfrage von Items mit einer Itemschwierigkeit die der aktuellen Personenfähigkeit entsprechen (da diese Items die Person mit einer Wahrscheinlichkeit von 50% löst).

Je größer die Information, die man über ein Item bzw. über eine Person sammelt, umso genauer kann man den Item bzw.
Personenparameter schätzen.
Daraus folgt:
Hat man einen fixen Test, so ist die Messgenauigkeit dieses Tests nicht bei allen Personen gleich.
Für die Items gilt: je stärker die Itemschwierigkeit von der durchschnittlichen Personenfähigkeit einer Gruppe abweicht umso ungenauer ist die Schätzung der Itemschwierigkeit.
Bei einem fixen Test ist die Messgenauigkeit nicht bei allen Personen gleich, denn je besser die Personenfähigkeit zur Itemschwierigkeit passt, desto besser kann man die Personenfähigkeit schätzen.
Tags: Informationsfunktion, Parameterschätzung
Quelle: F286
Quelle: F286
Welche Methoden zur Modellkontrolle gibt es?
Um zu überprüfen, ob die vorliegenden Items dem dichotom logistischen Modell von Rasch entsprechen, können verschiedene Modelltests herangezogen werden.
Dazu gehören z.B.
Bei den Modellkontrollen wird überprüft ob/welche Item nicht das Rasch-Modell erfüllen.
Es werden solange Items aus dem Test entfernt bis die Modelltests nicht mehr signifikant sind.
Müssen mehr als in etwa 20% der Items entfernt werden, sollten die verbleibenden Items an einer neuen Stichprobe abermals geprüft werden.
Dazu gehören z.B.
- die grafische Modellkontrolle,
- der z-Test nach Wald,
- der bedingte Likelihood Quotienten Test nach Andersen und
- der Martin Löf Test.
Bei den Modellkontrollen wird überprüft ob/welche Item nicht das Rasch-Modell erfüllen.
Es werden solange Items aus dem Test entfernt bis die Modelltests nicht mehr signifikant sind.
Müssen mehr als in etwa 20% der Items entfernt werden, sollten die verbleibenden Items an einer neuen Stichprobe abermals geprüft werden.
Tags: IRT, Modellkontrollen, Rasch-Modell
Quelle: F290
Quelle: F290
Wie erfolgt die grafische Modellkontrolle?
Für die grafische Modellkontrolle werden die Personen in zwei Gruppen eingeteilt und die Itemschwierigkeitsparameter in jeder Gruppe extra geschätzt.
Für die Einteilung in die zwei Gruppen können zwei Arten von Kriterien verwendet werden
Dann wird für die Itemschwierigkeitsparameter in jeder Gruppe extra geschätzt.
Für den Fall, dass ein Item dem Modell von Rasch entspricht, sollten die Schätzungen in beiden Stichproben in etwa gleich groß sein (=spezifische Objektivität).
Trägt man die Items in einem Koordinatensystem mit
- x=Schätzung in Gruppe 1 und
- y= Schätzung in Gruppe 2, so sollten Items, die dem Modell von Rasch entsprechen, nahe der 45° Geraden liegen.



Da die geschätzten Itemschwierigkeitsparameter eindeutig bis auf additive Konstanten (bzw. die Itemleichtigkeitsparameter eindeutig bis auf multiplikative Konstanten) sind, muss sicher gestellt werden, dass die Itemparameter in beiden Stichproben gleichartig normiert sind.
Für die Einteilung in die zwei Gruppen können zwei Arten von Kriterien verwendet werden
- intern (= Rohscore) oder
- extern (Eigenschaften der Personen z.B. Altersgruppen, Geschlecht, Gruppenzugehörigkeit…).
Dann wird für die Itemschwierigkeitsparameter in jeder Gruppe extra geschätzt.
Für den Fall, dass ein Item dem Modell von Rasch entspricht, sollten die Schätzungen in beiden Stichproben in etwa gleich groß sein (=spezifische Objektivität).
Trägt man die Items in einem Koordinatensystem mit
- x=Schätzung in Gruppe 1 und
- y= Schätzung in Gruppe 2, so sollten Items, die dem Modell von Rasch entsprechen, nahe der 45° Geraden liegen.



Da die geschätzten Itemschwierigkeitsparameter eindeutig bis auf additive Konstanten (bzw. die Itemleichtigkeitsparameter eindeutig bis auf multiplikative Konstanten) sind, muss sicher gestellt werden, dass die Itemparameter in beiden Stichproben gleichartig normiert sind.
Tags: Modellkontrolle, Rasch-Modell
Quelle: F291
Quelle: F291
Welche Methoden müssen zur Normierung der Itemschwierigkeit bzw. -leichtigkeit eingesetzt werden?
Für Itemschwierigkeiten ist die „Summe 0“ Normierung zu empfehlen (d.h. die Summe aller Itemschwierigkeiten ist 0).
Wenn dies nicht der Fall ist, dann können die Items nachträglich normiert werden. Man berechnet sich den Mittelwert und zieht diese von der Itemschwierigkeit ab.

Für Itemleichtigkeiten sollte die „Produkt 1“ Normierung verwendet werden (d.h. das Produkt aller Itemleichtigkeiten ist 1).

Wenn dies nicht der Fall ist, dann können die Items nachträglich normiert werden. Man berechnet sich den Mittelwert und zieht diese von der Itemschwierigkeit ab.

Für Itemleichtigkeiten sollte die „Produkt 1“ Normierung verwendet werden (d.h. das Produkt aller Itemleichtigkeiten ist 1).

Tags: Itemschwierigkeit, Modellkontrollen, Normierung, Rasch-Modell
Quelle: F297
Quelle: F297
Was ist der z-Test nach Wald?
(Modellkontrollen)
Beim z-Test nach Wald werden die in zwei Stichproben (A, B) erhobenen und normierten Itemschwierigkeitsparameter miteinander verglichen.

Ist der Betrag des z-Werts größer als der kritische z-Wert, ist das Ergebnis signifikant und das Modell von Rasch gilt für dieses Item nicht.
Da der z-Test pro Item erfolgt und demnach die Gefahr der Alpha Überhöhung gegeben ist, kann aus den z-Werten ein Globaltest für alle in einem Test enthaltenen Items berechnet werden.

Ist der -Wert größer als der kritische, ist das Ergebnis
-Wert größer als der kritische, ist das Ergebnis
signifikant und man muss zumindest das Item mit dem betragsmäßig größten z-Wert aus dem Test entfernen.
Dann muss der Test erneut durchgeführt werden.
Beim z-Test nach Wald werden die in zwei Stichproben (A, B) erhobenen und normierten Itemschwierigkeitsparameter miteinander verglichen.

Ist der Betrag des z-Werts größer als der kritische z-Wert, ist das Ergebnis signifikant und das Modell von Rasch gilt für dieses Item nicht.
Da der z-Test pro Item erfolgt und demnach die Gefahr der Alpha Überhöhung gegeben ist, kann aus den z-Werten ein Globaltest für alle in einem Test enthaltenen Items berechnet werden.

Ist der
 -Wert größer als der kritische, ist das Ergebnis
-Wert größer als der kritische, ist das Ergebnissignifikant und man muss zumindest das Item mit dem betragsmäßig größten z-Wert aus dem Test entfernen.
Dann muss der Test erneut durchgeführt werden.
Tags: Modellkontrollen, Rasch-Modell, z-Test
Quelle: F298
Quelle: F298
Was ist der LQT?
Bei Likelihood Quotienten Tests (LQT) werden die Likelihoods zweier Modelle miteinander verglichen.

Die beiden Modelle müssen drei Bedingungen erfüllen
Sind diese drei Bedingungen erfüllt, kann man den LQT in eine verteilte Prüfgröße umwandeln.
verteilte Prüfgröße umwandeln.

Beim bedingten LQT Test nach Andersen wird für Modell 1 angenommen, dass zwei (oder mehr) Gruppen von Personen unterschiedliche Itemparameter haben.
Bei Modell 2 wird davon ausgegangen, dass die Itemparameter in allen Gruppen gleich sind (= spezifische Objektivität).
Lässt sich kein Unterschied zwischen der Likelihood der beiden Modelle nachweisen(= nicht signifikantes Ergebnis), darf Modell 2 (und damit die Gültigkeit des RM) angenommen werden.

Die beiden Modelle müssen drei Bedingungen erfüllen
- Modell 1 muss ein echtes Obermodell von Modell 2 sein (d.h. dass Modell 2 durch Restriktionen von Parametern aus Modell 1 entsteht).
- Modell 2 darf nicht durch 0 setzen von Parametern entstehen.
- Modellgültigkeit von Modell 1 muss nachgewiesen sein.
Sind diese drei Bedingungen erfüllt, kann man den LQT in eine
 verteilte Prüfgröße umwandeln.
verteilte Prüfgröße umwandeln.
Beim bedingten LQT Test nach Andersen wird für Modell 1 angenommen, dass zwei (oder mehr) Gruppen von Personen unterschiedliche Itemparameter haben.
Bei Modell 2 wird davon ausgegangen, dass die Itemparameter in allen Gruppen gleich sind (= spezifische Objektivität).
Lässt sich kein Unterschied zwischen der Likelihood der beiden Modelle nachweisen(= nicht signifikantes Ergebnis), darf Modell 2 (und damit die Gültigkeit des RM) angenommen werden.
Tags: LQT, Modellkontrollen, Rasch-Modell
Quelle: F300
Quelle: F300
Was ist der Martin Löf Test?
(Modellkontrollen)
Der Martin Löf Test basiert im Wesentlichen auf derselben Annahme wie der bedingte LQT von Andersen, jedoch werden nicht die Personen, sondern die Items in zwei Gruppen aufgeteilt. Demnach wird geprüft, ob die Schätzungen der Personenparameter in beiden Itemgruppen gleich sind.
Auch hier deutet ein signifikantes Ergebnis auf eine Verletzung der Annahmen des Rasch Modells bei zumindest einem Item hin.
Es werden solange Items aus dem Test entfernt bis die Modelltests nicht mehr signifikant sind.
Müssen mehr als in etwa 20% der Items entfernt werden, sollten die verbleibenden Items an einer neuen Stichprobe abermals geprüft werden.
Der Martin Löf Test basiert im Wesentlichen auf derselben Annahme wie der bedingte LQT von Andersen, jedoch werden nicht die Personen, sondern die Items in zwei Gruppen aufgeteilt. Demnach wird geprüft, ob die Schätzungen der Personenparameter in beiden Itemgruppen gleich sind.
Auch hier deutet ein signifikantes Ergebnis auf eine Verletzung der Annahmen des Rasch Modells bei zumindest einem Item hin.
Es werden solange Items aus dem Test entfernt bis die Modelltests nicht mehr signifikant sind.
Müssen mehr als in etwa 20% der Items entfernt werden, sollten die verbleibenden Items an einer neuen Stichprobe abermals geprüft werden.
Tags: Modellkontrollen, Rasch-Modell
Quelle: F304
Quelle: F304
Was zeigen diese Ausdruck? Was kann interpretiert werden?




Ein Test zur Erfassung von Raumvorstellung besteht aus 13 dichotomen Items. Es soll geprüft werden, ob die Items dem Modell von Rasch entsprechen. Als Teilungskriterien werden der Mittelwert und der Median des Rohscores herangezogen.


Grafische Darstellung:



Grafische Darstellung:

Tags: Modellkontrollen, Rasch-Modell, z-Test
Quelle: F306
Quelle: F306
Was zeigt dieser Ausdruck?


Modellkontrolle:

Der Martin Löf Test basiert im Wesentlichen auf derselben Annahme wie der bedingte LQT von Andersen, jedoch werden nicht die Personen, sondern die Items in zwei Gruppen aufgeteilt. Demnach wird geprüft, ob die Schätzungen der Personenparameter in beiden Itemgruppen gleich sind.
Auch hier deutet ein signifikantes Ergebnis auf eine Verletzung der Annahmen des Rasch Modells bei zumindest einem Item hin.
Es werden solange Items aus dem Test entfernt bis die Modelltests nicht mehr signifikant sind.
Müssen mehr als in etwa 20% der Items entfernt werden, sollten die verbleibenden Items an einer neuen Stichprobe abermals geprüft werden.

Der Martin Löf Test basiert im Wesentlichen auf derselben Annahme wie der bedingte LQT von Andersen, jedoch werden nicht die Personen, sondern die Items in zwei Gruppen aufgeteilt. Demnach wird geprüft, ob die Schätzungen der Personenparameter in beiden Itemgruppen gleich sind.
Auch hier deutet ein signifikantes Ergebnis auf eine Verletzung der Annahmen des Rasch Modells bei zumindest einem Item hin.
Es werden solange Items aus dem Test entfernt bis die Modelltests nicht mehr signifikant sind.
Müssen mehr als in etwa 20% der Items entfernt werden, sollten die verbleibenden Items an einer neuen Stichprobe abermals geprüft werden.
Tags: Martin Löf Test, Modellkontrollen, Rasch-Modell
Quelle: F310
Quelle: F310
Welche weiteren Modelle neben der IRT gibt es (Beispiele)?
Ausgehende von den Ideen von Georg Rasch wurden zahlreiche weitere Modelle entwickelt. Im Folgenden werden
kurz vorgestellt.
- die Modelle von Birnbaum (1968),
- das linear logistische Testmodell (LLTM) und
- die Erweiterung auf rangskalierte Daten
kurz vorgestellt.
Tags: IRT
Quelle: F312
Quelle: F312
Was sind die Birnbaum Modelle? Beschreibe diese.
Birnbaum (1968) stellte zwei Erweiterungen des dichotom logistischen Modells von Rasch vor, indem er unterschiedliche Diskriminations- und Rateparameter pro Item erlaubt.
Bei diesen Modellen handelt es sich um
Bei beiden Modellen ergeben sich wegen der relativ großen Zahl an Modellparametern häufig Probleme bei der Parameterschätzung.
Das zwei Parameter logistische Modell
Bei diesem Modell gibt es pro Item zwei Parameter, nämlich
Die Lösungswahrscheinlichkeit eines Items i durch Person v ist gegeben durch

Aufgrund der unterschiedlichen Diskriminationsparameter gibt es in diesem Modell schneidende IC Kurven, sodass die spezifische Objektivität bei diesem Modell nicht gegeben ist.

Das drei Parameter logistische Modell
Bei diesem Modell gibt es pro Item drei Parameter, nämlich
Die Lösungswahrscheinlichkeit eines Items i durch Person v ist gegeben durch

Auch hier schneiden die IC Kurven einander

Bei diesen Modellen handelt es sich um
- das zwei Parameter logistische Modell und
- das drei Parameter logistische Modell.
Bei beiden Modellen ergeben sich wegen der relativ großen Zahl an Modellparametern häufig Probleme bei der Parameterschätzung.
Das zwei Parameter logistische Modell
Bei diesem Modell gibt es pro Item zwei Parameter, nämlich
- den Itemschwierigkeitsparamter und
- den Diskriminationsparameter.
Die Lösungswahrscheinlichkeit eines Items i durch Person v ist gegeben durch

Aufgrund der unterschiedlichen Diskriminationsparameter gibt es in diesem Modell schneidende IC Kurven, sodass die spezifische Objektivität bei diesem Modell nicht gegeben ist.

Das drei Parameter logistische Modell
Bei diesem Modell gibt es pro Item drei Parameter, nämlich
- den Itemschwierigkeitsparamter,
- den Diskriminationsparameter und
- die Ratewahrscheinlichkeit.
Die Lösungswahrscheinlichkeit eines Items i durch Person v ist gegeben durch

Auch hier schneiden die IC Kurven einander

Tags: Birnbaum Modelle, IRT
Quelle: F313
Quelle: F313
Was ist das linear logistische Testmodell (LLTM)?
Das LLTM geht auf Scheiblechner (1972) und Fischer (1972, 1973) zurück und stellt ein restriktiveres Modell als das dichotom logistische Modell von Rasch dar.
Die ursprüngliche Idee war es, die Schwierigkeit eines dem Modell von Rasch entsprechenden Items auf die Schwierigkeit jener kognitiven Fertigkeiten zurückzuführen, die aufgrund theoretischer Überlegungen im Vorfeld der Lösung des Items zugrunde liegen.



Zur Kontrolle der Gültigkeit des LLTM werden die laut LLTM geschätzten Parameter mit den aus dem dichotom logistischen Modell von Rasch mit Hilfe einer der bereits bekannten Modellkontrollen verglichen.
Der bekannteste Test, der auf dem LLTM basiert ist der Wiener Matrizen Test (WMT) von Formann und Piswanger (1979).
Abgesehen von der ursprünglichen Idee, kann das LLTM auch z.B. für den Vergleich von Gruppen, Positionseffekten, oder zur Modellierung des Einflusses von Lernprozessen (Veränderungsmessung) verwendet werden.
Die ursprüngliche Idee war es, die Schwierigkeit eines dem Modell von Rasch entsprechenden Items auf die Schwierigkeit jener kognitiven Fertigkeiten zurückzuführen, die aufgrund theoretischer Überlegungen im Vorfeld der Lösung des Items zugrunde liegen.



Zur Kontrolle der Gültigkeit des LLTM werden die laut LLTM geschätzten Parameter mit den aus dem dichotom logistischen Modell von Rasch mit Hilfe einer der bereits bekannten Modellkontrollen verglichen.
Der bekannteste Test, der auf dem LLTM basiert ist der Wiener Matrizen Test (WMT) von Formann und Piswanger (1979).
Abgesehen von der ursprünglichen Idee, kann das LLTM auch z.B. für den Vergleich von Gruppen, Positionseffekten, oder zur Modellierung des Einflusses von Lernprozessen (Veränderungsmessung) verwendet werden.
Tags: IRT, LLTM, Rasch-Modell
Quelle: F318
Quelle: F318
Berechne die Itemschwierigkeiten für jedes Item:


Die ursprüngliche Idee war es, die Schwierigkeit eines dem Modell von Rasch entsprechenden Items auf die Schwierigkeit jener kognitiven Fertigkeiten zurückzuführen, die aufgrund theoretischer Überlegungen im Vorfeld der Lösung des Items zugrunde liegen.






Tags: IRT, Itemschwierigkeit, LLTM
Quelle: F318
Quelle: F318
Was ist das Partial Credit Modell?
Das Partial Credit Model ist das Rasch Modell für ordinale Daten. Die dahinter liegende Idee ist eine Verallgemeinerung des dichotom logistischen Modells von Rasch. Für letzteres wurde gezeigt, dass es neben der IC Kurve für das Lösen des Items auch eine IC Kurve für das nicht Lösen eines Items gibt.

Hat man nun nicht nur zwei, sondern z.B. vier Kategorien, könnten die resultierenden IC Kurven folgendermaßen aussehen.

Dadurch wird für jeden Fähigkeitsparameter die Wahrscheinlichkeit der Antwort in Kategorie x modelliert.
Jene Stellen, ab denen eine andere Kategorie als wahrscheinlichste gilt, werden Schwellen genannt.
Prinzipiell können die Schwellen in jedem Item anders sein.
Da daraus eine sehr große Zahl an Parameter resultiert, können zusätzliche Annahmen getroffen werden, die zu unterschiedlichen Modellen führen. Diese sind
Mittels das Partial Credit Modells kann geprüft werden, ob die Stufen eines Items tatsächlich rangskaliert sind. Die Ordnung der Antwortkategorien zeigt sich daran, dass die Schnittpunkte zweier benachbarter Kategorien „geordnet“ sind. Das bedeutet, dass z.B. der Übergang von Kategorie 0 auf 1 bei einer niedrigeren Personenfähigkeit erfolgt, als der Übergang von Kategorie 1 auf 2 usw.


Hat man nun nicht nur zwei, sondern z.B. vier Kategorien, könnten die resultierenden IC Kurven folgendermaßen aussehen.

Dadurch wird für jeden Fähigkeitsparameter die Wahrscheinlichkeit der Antwort in Kategorie x modelliert.
Jene Stellen, ab denen eine andere Kategorie als wahrscheinlichste gilt, werden Schwellen genannt.
Prinzipiell können die Schwellen in jedem Item anders sein.
Da daraus eine sehr große Zahl an Parameter resultiert, können zusätzliche Annahmen getroffen werden, die zu unterschiedlichen Modellen führen. Diese sind
- das Ratingskalen Modell,
- das Äquidstanzmodell und
- das Dispersionsmodell.
Mittels das Partial Credit Modells kann geprüft werden, ob die Stufen eines Items tatsächlich rangskaliert sind. Die Ordnung der Antwortkategorien zeigt sich daran, dass die Schnittpunkte zweier benachbarter Kategorien „geordnet“ sind. Das bedeutet, dass z.B. der Übergang von Kategorie 0 auf 1 bei einer niedrigeren Personenfähigkeit erfolgt, als der Übergang von Kategorie 1 auf 2 usw.

Tags: IRT, Partial Credit Modell, Rasch-Modell
Quelle: F322
Quelle: F322
Welche Arten von Modellen gibt es beim Partial Credit Modell?
Prinzipiell können die Schwellen in jedem Item anders sein.
Da daraus eine sehr große Zahl an Parameter resultiert, können zusätzliche Annahmen getroffen werden, die zu unterschiedlichen Modellen führen. Diese sind




Mittels das Partial Credit Modells kann geprüft werden, ob die Stufen eines Items tatsächlich rangskaliert sind. Die Ordnung der Antwortkategorien zeigt sich daran, dass die Schnittpunkte zweier benachbarter Kategorien „geordnet“ sind. Das bedeutet, dass z.B. der Übergang von Kategorie 0 auf 1 bei einer niedrigeren Personenfähigkeit erfolgt, als der Übergang von Kategorie 1 auf 2 usw.

Da daraus eine sehr große Zahl an Parameter resultiert, können zusätzliche Annahmen getroffen werden, die zu unterschiedlichen Modellen führen. Diese sind
- das Ratingskalen Modell,
- das Äquidstanzmodell und
- das Dispersionsmodell.




Mittels das Partial Credit Modells kann geprüft werden, ob die Stufen eines Items tatsächlich rangskaliert sind. Die Ordnung der Antwortkategorien zeigt sich daran, dass die Schnittpunkte zweier benachbarter Kategorien „geordnet“ sind. Das bedeutet, dass z.B. der Übergang von Kategorie 0 auf 1 bei einer niedrigeren Personenfähigkeit erfolgt, als der Übergang von Kategorie 1 auf 2 usw.

Tags: IRT, Partial Credit Modell
Quelle: F325
Quelle: F325
Welche Arten von Skalenniveaus werden unterschieden?
Nominalskala
Ordinalskala
Intervallskala:
Rationalskala (Verhältnisskala)
Für alle Skalen gilt: In übergeordneten („höheren“) Skalen sind alle Transformationen der niedrigeren Skalen auch möglich.
- nur Unterscheidung: gleich oder ungleich
- immer diskret
- z.B.: Religion, Geschlecht, Nationalität, …
Ordinalskala
- größer/kleiner (über Abstände aber keine Aussage)
- z.B.: Schulnoten, Einkommensklassen, …
Intervallskala:
- Metrische Skala
- Abstände exakt bestimmbar
- KEIN natürlicher Nullpunkt
- Differenz- und Summenbildung sinnvoll ... Mittelwert erst ab dieser Skala sinnvoll
- z.B.: Temperatur (Celsius), IQ-Skala, …
Rationalskala (Verhältnisskala)
- Metrisch
- Natürlicher Nullpunkt
- Multiplikative Transformationen möglich
- z.B.: Gewicht, Geld, Körpergröße, Zeit, …
Für alle Skalen gilt: In übergeordneten („höheren“) Skalen sind alle Transformationen der niedrigeren Skalen auch möglich.
Tags: Skalenniveau
Quelle: Tutorium 0
Quelle: Tutorium 0
Welche Häufigkeiten können unterschieden werden?
- Absolut: Anzahl
- Relativ: Anzahl in Relation zur Grundmenge
- Kumulativ (kumuliert): - Merkmal mindestens ordinalskaliert - geordnet- Summe inkl. aller vorherigen Häufigkeiten (absolut oder relativ)

Tags: Häufigkeit
Quelle: Tutorium 0
Quelle: Tutorium 0
Was versteht man unter Population und Stichprobe? Was versteht man unter Populationsparameter und Stichprobenschätzer?
Population = Grundgesamtheit
In empirischer Forschung: Menge aller potentiellen Untersuchungsobjekte
Stichprobe: Teilmenge der Population ... Untersuchte Objekte
Ziel: Verallgemeinerung von Ergebnissen der Stichprobe auf Population
Populationsparameter vs. Stichprobenschätzer
In empirischer Forschung: Menge aller potentiellen Untersuchungsobjekte
Stichprobe: Teilmenge der Population ... Untersuchte Objekte
Ziel: Verallgemeinerung von Ergebnissen der Stichprobe auf Population
Populationsparameter vs. Stichprobenschätzer
- Populationsparameter gelten in der Population - im Allgemeinen NICHT bekannt- „wahrer Wert“
- Stichprobenschätzer dienen als Schätzung für die Populationsparameter z.B.: Erwartungswert μ geschätzt durch
 Varianz σ2 geschätzt durch S2Korrelation
Varianz σ2 geschätzt durch S2Korrelation  geschätzt durch
geschätzt durch 
Tags: Population, Stichprobe
Quelle: Tutorium 0
Quelle: Tutorium 0
Welche Arten von Hypothesen können unterschieden werden?
Forschungsfragen können als statistische Hypothesen formuliert werden
Gerichtete Hypothese: Annahme über die Richtung des Zusammenhangs bzw. Unterschieds
z.B.: H0: μ1 ≤ μ2 vs. H1: μ1 > μ2
z.B.: H0: ρX,Y ≤ 0 vs. H1: ρX,Y > 0
Ungerichtete Hypothese: Keine Annahme über die Richtung des Zusammenhangs bzw. Unterschieds
z.B.: H0: μ1 = μ2 vs. H1: μ1 ≠ μ2
z.B.: H0: ρX,Y = 0 vs. H1: ρX,Y ≠ 0
Gerichtet vs. Ungerichtet: Stichwort: einseitige vs. zweiseitige Testung
Prüfung von (statistischen) Hypothesen mittels Teststatistiken und deren Verteilungen (z.B.: NV-Test: z-Wert, t-Test: t-Verteilung, F-Test: F-Verteilung,…)
- diese mittels jeweiligem Test überprüfen
- Null-Hypothese H0 vs. Alternativhypothese H1 z.B.: H0: μ1 = μ2 vs. H1: μ1 ≠ μ2z.B.: H0: ρX,Y = 0 vs. H1: ρX,Y ≠ 0
Gerichtete Hypothese: Annahme über die Richtung des Zusammenhangs bzw. Unterschieds
z.B.: H0: μ1 ≤ μ2 vs. H1: μ1 > μ2
z.B.: H0: ρX,Y ≤ 0 vs. H1: ρX,Y > 0
Ungerichtete Hypothese: Keine Annahme über die Richtung des Zusammenhangs bzw. Unterschieds
z.B.: H0: μ1 = μ2 vs. H1: μ1 ≠ μ2
z.B.: H0: ρX,Y = 0 vs. H1: ρX,Y ≠ 0
Gerichtet vs. Ungerichtet: Stichwort: einseitige vs. zweiseitige Testung
Prüfung von (statistischen) Hypothesen mittels Teststatistiken und deren Verteilungen (z.B.: NV-Test: z-Wert, t-Test: t-Verteilung, F-Test: F-Verteilung,…)
Tags: Hypothese
Quelle: Tutorium 0
Quelle: Tutorium 0
Was ist das  -Niveau und der p-Wert?
-Niveau und der p-Wert?
 -Niveau und der p-Wert?
-Niveau und der p-Wert?α = Irrtumswahrscheinlichkeit
.... Wahrscheinlichkeit für Fehler 1. Art (α-Fehler)
Fehler 1. Art: H0 verworfen obwohl sie wahr ist
(Fehler 2. Art: H0 beibehalten obwohl H1 wahr ist)
p-Wert
Unter Annahme, dass H0 gilt:
Wahrscheinlichkeit eine Teststatistik zu erhalten, die gleich oder noch „extremer“ als die beobachtete Statistik ist
Gibt Ausmaß der Plausibilität der H0
NICHT: Wahrscheinlichkeit der Daten
NICHT: Wahrscheinlichkeit der H0
Wenn p ≤ α ... signifikant ... H0 verwerfen
.... Wahrscheinlichkeit für Fehler 1. Art (α-Fehler)
Fehler 1. Art: H0 verworfen obwohl sie wahr ist
(Fehler 2. Art: H0 beibehalten obwohl H1 wahr ist)
- VORHER festlegen!
- Gängige Konvention: α = .05 oder .01
- Achtung: manchmal ist H0 die „gewünschte“ Hypothese (z.B.: KS-Test auf NV) ... in diesem Fall höheres α falls strengere Prüfung nötig
p-Wert
Unter Annahme, dass H0 gilt:
Wahrscheinlichkeit eine Teststatistik zu erhalten, die gleich oder noch „extremer“ als die beobachtete Statistik ist
Gibt Ausmaß der Plausibilität der H0
NICHT: Wahrscheinlichkeit der Daten
NICHT: Wahrscheinlichkeit der H0
Wenn p ≤ α ... signifikant ... H0 verwerfen
Tags: Hypothese, Irrtumswahrscheinlichkeit
Quelle: Tutorium 0
Quelle: Tutorium 0
Wieviel % der Population umfassen die Bereiche um die 1. , 2. und 3.  (Standardabweichung)?
(Standardabweichung)?
 (Standardabweichung)?
(Standardabweichung)?μ ± 1∙σ ≈ 68.3 % der Population
μ ± 2∙σ ≈ 95.4 % der Population
μ ± 3∙σ ≈ 99.7 % der Population
μ ± 2∙σ ≈ 95.4 % der Population
μ ± 3∙σ ≈ 99.7 % der Population
Tags: Normwerte, Population, Standardabweichung
Quelle: Tutorium 1
Quelle: Tutorium 1
Person X erreicht in einem Test 54 Punkte. Durchschnittlich sind 45 (= μ) Punkte bei einer Standardabweichung von 12 (=σ) zu erwarten.
Welchem IQ-Wert, T-Wert und Z-Wert entspricht das Testergebnis?
Welchem IQ-Wert, T-Wert und Z-Wert entspricht das Testergebnis?

Tags: Berechnung, Normwerte
Quelle: Tutorium 1
Quelle: Tutorium 1
Eine Person erreicht in einer Intelligenz-Test-Batterie einen IQ-Wert von 106.
Welchem Prozentrang entspricht diese Leistung?
Welchem Prozentrang entspricht diese Leistung?

Tags: Berechnung, Normwerte, Prozentränge
Quelle: Tutorium 1
Quelle: Tutorium 1
Wie könne nicht normalverteilte Testwerte in eine Normalverteilung transformiert werden?
Flächentransformation
Nicht normalverteilte Testkennwerte können über die Prozentränge (aus kumulierter relativer Häufigkeit) in eine annähernde Normalverteilung übergeführt werden.
Achtung: Verzerrungen wenn die ursprüngliche Verteilung stark von der NV abweicht.
Genaues Vorgehen + Beispiel: Moosbrugger & Kelava, ab S.96


Nicht normalverteilte Testkennwerte können über die Prozentränge (aus kumulierter relativer Häufigkeit) in eine annähernde Normalverteilung übergeführt werden.
Achtung: Verzerrungen wenn die ursprüngliche Verteilung stark von der NV abweicht.
Genaues Vorgehen + Beispiel: Moosbrugger & Kelava, ab S.96


Tags: Flächentransformation, Normalverteilung
Quelle: Tutorium 1
Quelle: Tutorium 1
Test A und Test B wurden zwei verschiedenen Gruppen vorgegeben.
Können die beiden Tests A und B als parallel angenommen werden? Beschreibe das Vorgehen.

Können die beiden Tests A und B als parallel angenommen werden? Beschreibe das Vorgehen.

Zwei Tests (bzw. Items) A und B sind parallel, wenn
 gilt.
gilt.
.... Tests (Items) erfassen das Merkmal gleich „genau“
Vorgehen
# * Mittelwerte und Varianzen (oder SD) berechnen:
Beide p-Werte nicht signifikant. Daher können die Tests als parallel angenommen werden.
Allerdings: kein Beweis für die Parallelität (strenge Prüfung nicht möglich, da die wahren Werte unbekannt sind)
 gilt.
gilt. .... Tests (Items) erfassen das Merkmal gleich „genau“
Vorgehen
# * Mittelwerte und Varianzen (oder SD) berechnen:

Beide p-Werte nicht signifikant. Daher können die Tests als parallel angenommen werden.
Allerdings: kein Beweis für die Parallelität (strenge Prüfung nicht möglich, da die wahren Werte unbekannt sind)
Was zeigt dieser SPSS-Ausdruck hinsichtlich der Parallelität zweier Tests?


Vorgehen
1.Mittelwerte und Varianzen (oder SD) berechnen:
2.Mittelwerte vergleichen ... T-Test (unabh. SP)
3.Varianzen vergleichen ... z.B. Levene-Test
(2 & 3 werden im SPSS bei „T-Test bei unabhängigen Stichproben“ ausgegeben)
Beide p-Werte nicht signifikant. Daher können die Tests als parallel angenommen werden.
Allerdings: kein Beweis für die Parallelität (strenge Prüfung nicht möglich, da die wahren Werte unbekannt sind)
1.Mittelwerte und Varianzen (oder SD) berechnen:
2.Mittelwerte vergleichen ... T-Test (unabh. SP)
3.Varianzen vergleichen ... z.B. Levene-Test
(2 & 3 werden im SPSS bei „T-Test bei unabhängigen Stichproben“ ausgegeben)
Beide p-Werte nicht signifikant. Daher können die Tests als parallel angenommen werden.
Allerdings: kein Beweis für die Parallelität (strenge Prüfung nicht möglich, da die wahren Werte unbekannt sind)
Tags: Berechnung, Parallelität
Quelle: Tutorium 1
Quelle: Tutorium 1
Wie hoch ist die Paralleltest-Reliabilität von Test A und B?


Korrelation berechnen: rêl = .715
(SPSS: Analysieren - Korrelation -Bivariat (Pearson))
(SPSS: Analysieren - Korrelation -Bivariat (Pearson))
Tags: Reliabilität
Quelle: Tutorium 1
Quelle: Tutorium 1
Ein Test besteht aus 50 parallelen Items. Der Test ist auf T-Werte geeicht und die Reliabilität beträgt 0.89. Der Test wird nun auf 35 parallele Items gekürzt.
a) Wie hoch ist die Reliabilität des neuen Tests?
b) Welchen Mittelwert und welche Varianz sind im kürzeren Test zu erwarten?
a) Wie hoch ist die Reliabilität des neuen Tests?
b) Welchen Mittelwert und welche Varianz sind im kürzeren Test zu erwarten?


Tags: Berechnung, Reliabilität
Quelle: Tutorium 1
Quelle: Tutorium 1
Ein Test besteht aus 20 parallelen Items. Die Reliabilität des Tests beträgt 0.75.
Wie viele zusätzliche (parallele) Items werden benötigt, wenn man eine Reliabilität von 0.85 anstrebt?
Wie viele zusätzliche (parallele) Items werden benötigt, wenn man eine Reliabilität von 0.85 anstrebt?


Mindestens 38 Items werden benötigt, um die gewünschte Reliabilität zu erhalten. - 18 Items mehr als im Originaltest
Tags: Berechnung, Reliabilität
Quelle: Tutorium 1
Quelle: Tutorium 1
Nicht normierter Test X mit Mittelwert 5, Standardabweichung 5. Eine TP hat in einem anderen Test einen T-Wert von 60 erreicht.
Welchem X-Wert entspricht dieser?
Welchem X-Wert entspricht dieser?

Tags: Berechnung, Normwerte
Quelle: Tutorium 2
Quelle: Tutorium 2
Man denkt sich einen neuen Norm-Wert aus: "E"-Wert mit μ=5 und σ=10.
Welchem E-Wert entspricht ein T von 55?
Welchem E-Wert entspricht ein T von 55?

Tags: Berechnung, Normwerte
Quelle: Tutorium 2
Quelle: Tutorium 2
Eine Person erzielt in einem Test einen Rohwert von 56 Punkten. Es sei bekannt, dass der Mittelwert des Tests 60 Punkte, die Standardabweichung des Tests 8 Punkte und die Reliabilität rel= 0.89 beträgt.
Geben Sie Konfidenzintervalle für 95 % und 99 % auf Basis der Messfehlervarianz an und vergleichen Sie die Ergebnisse!
Geben Sie Konfidenzintervalle für 95 % und 99 % auf Basis der Messfehlervarianz an und vergleichen Sie die Ergebnisse!

Tags: Berechnung, Konfidenzintervalle
Quelle: Tutorium 2
Quelle: Tutorium 2
Person A erzielt in einem Test einen IQ von 113. Die im Testmanual angegebene Testreliabilität beträgt rel= 0.82.
Geben Sie ein möglichst genaues Konfidenzintervall für den True-Score an!
(99%-Wahrscheinlichkeit)
Geben Sie ein möglichst genaues Konfidenzintervall für den True-Score an!
(99%-Wahrscheinlichkeit)

Tags: Berechnung, Konfidenzintervalle
Quelle: Tutorium 2
Quelle: Tutorium 2
Person A erzielt in einem Test einen IQ von 113. Person B erzielt im gleichen Test einen IQ von 120.
Die im Testmanual angegebene Testreliabilität beträgt rel= 0.82.
Besteht ein statistisch signifikanter Unterschied zwischen den Leistungen von A und B ?
Die im Testmanual angegebene Testreliabilität beträgt rel= 0.82.
Besteht ein statistisch signifikanter Unterschied zwischen den Leistungen von A und B ?


KIs der Personen A und B überlappen sich - Kein signifikanter Unterschied
Tags: Berechnung, Konfidenzintervalle
Quelle: Tutorium 2
Quelle: Tutorium 2
Zwei Bewerber um eine Stelle wurden mit einem Reasoning-Test mit einer Reliabilität von 0.90 getestet, wobei A einen T-wert von 20 und B einen T-Wert von 24 erzielt.
Chef behauptet, dass B eindeutig besser für die Stelle.
α = 0.05
Chef behauptet, dass B eindeutig besser für die Stelle.
α = 0.05
Vergleich der Ergebnisse mittels Konfidenz-Intervallen
Berechnung auf Basis der Messfehlervarianz:

Berechnung auf Basis der Messfehlervarianz:

- KIs überschneiden sich
- Von statistisch signifikantem Unterschied der Testergebnisse der beiden Bewerber kann nicht ausgegangen werden
Tags: Berechnung, Konfidenzintervalle
Quelle: Tutorium 2
Quelle: Tutorium 2
Zwei Bewerber um eine Stelle wurden mit einem Reasoning-Test mit einer Reliabilität von 0.90 getestet, wobei A einen T-wert von 20 und B einen T-Wert von 24 erzielt.
Welche Reliabilität müsste der Test aufweisen, dass von einem statistisch signifikanten Unterschied der Ergebnisse ausgegangen werden könnte?
Welche Reliabilität müsste der Test aufweisen, dass von einem statistisch signifikanten Unterschied der Ergebnisse ausgegangen werden könnte?
Konfidenzintervalle dürften sich nicht überschneiden. D.h. dürften maximal [a, 20+2) bzw. (24-2, b] sein.


Tags: Berechnung, Konfidenzintervalle, Reliabilität
Quelle: Tutorium 2
Quelle: Tutorium 2
Wie hoch ist die Split-Half Realibilität wenn die Korrelation der Summenscores folgendes Ergebnis zeigt?


1. Möglichkeit die Split-Half Reliabilität zu berechnen:
-Test teilen (z.B. gerade/ungerade Items)
-Summenscores für Testteile berechnen
-Korrelation für Summenscores berechnen
-Mittels Korrekturformel geschätzte Reliabilität berechnen

Korrelation der Summenscores: r(X1, X2)=0.547
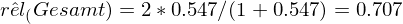
Anmerkung - 2. Möglichkeit:
2. Möglichkeit:
Analysieren – Skalierung – Reliabilitätsanalyse
- Modell: Split-Half
- Achtung bei Reihenfolge der Items: Erste Hälfte wird Teil 1 und zweite Hälfte Teil 2
- Ergebnis: Spearman-Brown-Koeffizient

-Test teilen (z.B. gerade/ungerade Items)
-Summenscores für Testteile berechnen
-Korrelation für Summenscores berechnen
-Mittels Korrekturformel geschätzte Reliabilität berechnen

Korrelation der Summenscores: r(X1, X2)=0.547
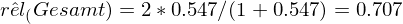
Anmerkung - 2. Möglichkeit:
2. Möglichkeit:
Analysieren – Skalierung – Reliabilitätsanalyse
- Modell: Split-Half
- Achtung bei Reihenfolge der Items: Erste Hälfte wird Teil 1 und zweite Hälfte Teil 2
- Ergebnis: Spearman-Brown-Koeffizient

Tags: Korrelation, Reliabilität
Quelle: Tutorium 2
Quelle: Tutorium 2
Die Korrelation eines Tests zur Messung der Konzentrationsfähigkeit (X) mit einem Außenkriterium „Konzentrationsleistung in der Schule“ (Y) sei r(X,Y)=0.35 ... vâl
Es sei bekannt, dass die Reliabilität des Tests 0.89 und die des Außenkriteriums 0.54 beträgt.
Wie hoch wäre die Validität des Tests, wenn man das Außenkriterium (Y) fehlerfrei erheben könnte?
Es sei bekannt, dass die Reliabilität des Tests 0.89 und die des Außenkriteriums 0.54 beträgt.
Wie hoch wäre die Validität des Tests, wenn man das Außenkriterium (Y) fehlerfrei erheben könnte?

Tags: Berechnung, Validität
Quelle: Tutorium 2
Quelle: Tutorium 2
Die Korrelation eines Tests zur Messung der Konzentrationsfähigkeit (X) mit einem Außenkriterium „Konzentrationsleistung in der Schule“ (Y) sei r(X,Y)=0.35 ... vâl
Es sei bekannt, dass die Reliabilität des Tests 0.89 und die des Außenkriteriums 0.54 beträgt.
Wie hoch wäre die Validität des Tests, wenn man das Testergebnis (X) fehlerfrei erheben könnte?
Es sei bekannt, dass die Reliabilität des Tests 0.89 und die des Außenkriteriums 0.54 beträgt.
Wie hoch wäre die Validität des Tests, wenn man das Testergebnis (X) fehlerfrei erheben könnte?

Tags: Berechnung, Validität
Quelle: Tutorium 2
Quelle: Tutorium 2
Die Korrelation eines Tests zur Messung der Konzentrationsfähigkeit (X) mit einem Außenkriterium „Konzentrationsleistung in der Schule“ (Y) sei r(X,Y)=0.35 ... vâl
Es sei bekannt, dass die Reliabilität des Tests 0.89 und die des Außenkriteriums 0.54 beträgt.
Wie hoch wäre die Validität des Tests, wenn man Testergebnis (X) und Außenkriterium (Y) fehlerfrei erheben könnte?
Es sei bekannt, dass die Reliabilität des Tests 0.89 und die des Außenkriteriums 0.54 beträgt.
Wie hoch wäre die Validität des Tests, wenn man Testergebnis (X) und Außenkriterium (Y) fehlerfrei erheben könnte?

Tags: Berechnung, Validität
Quelle: Tutorium 2
Quelle: Tutorium 2
Es sei bekannt, dass 60 % jener Personen, die sich für eine Stelle bewerben auch wirklich dafür geeignet sind. Zur Auswahl der Personen wird ein Test mit einer Validität von 0.3 verwendet.
Wie hoch ist die Wahrscheinlichkeit, dass die aus 10 BewerberInnen aufgrund des Tests ausgewählte Person wirklich für die ausgeschriebene Stelle geeignet ist?
Wie hoch ist die Wahrscheinlichkeit, dass die aus 10 BewerberInnen aufgrund des Tests ausgewählte Person wirklich für die ausgeschriebene Stelle geeignet ist?
GR = 0.6
SR = 0.1
val = 0.3
0.79

SR = 0.1
val = 0.3
0.79

Tags: Taylor-Russell-Tafeln
Quelle: Tutorium 2
Quelle: Tutorium 2
Es sei bekannt, dass 60 % jener Personen, die sich für eine Stelle bewerben auch wirklich dafür geeignet sind.
Wie hoch müsste die Validität des Tests sein, damit die Wahrscheinlichkeit, dass eine aus 10 BewerberInnen aufgrund des Tests ausgewählte Person, auch wirklich geeignet ist, 90 % beträgt?
Wie hoch müsste die Validität des Tests sein, damit die Wahrscheinlichkeit, dass eine aus 10 BewerberInnen aufgrund des Tests ausgewählte Person, auch wirklich geeignet ist, 90 % beträgt?
GR = 0.6
SR = 0.1
P(geeignet) = 0.9
... Validität = 0.5

SR = 0.1
P(geeignet) = 0.9
... Validität = 0.5

Tags: Taylor-Russell-Tafeln
Quelle: Tutorium 2
Quelle: Tutorium 2
Ein Test besteht aus 40 parallelen Items. Die Korrelation des Tests mit einem Außenkriterium beträgt r(x, y)=0.30. Die Reliabilität des Tests beträgt rel=0.75.
Wie hoch ist die Validität, wenn man den Test auf 35 parallele Items verkürzt?
Wie hoch ist die Validität, wenn man den Test auf 35 parallele Items verkürzt?

Tags: Berechnung, Reliabilität
Quelle: Tutorium 2
Quelle: Tutorium 2
Ein Test besteht aus 40 parallelen Items. Die Korrelation des Tests mit einem Außenkriterium beträgt r(x, y)=0.30. Die Reliabilität des Tests beträgt rel=0.75.
Um wie viele parallele Items müsste man den Test erweitern, wenn man eine Validität von 0.32 anstrebt?
Um wie viele parallele Items müsste man den Test erweitern, wenn man eine Validität von 0.32 anstrebt?


Der Test müsste um mindestens 38 Items verlängert werden um die gewünschte Validität von 0.32 zu erhalten.
Tags: Berechnung, Reliabilität
Quelle: Tutorium 2
Quelle: Tutorium 2
Bei einer Faktorenanalyse wurden 2 Faktoren extrahiert. Die Ladungen der Faktoren auf den 5 Items lauten folgendermaßen:

Wie hoch ist die Korrelation zwischen den Items 2 und 3?

Wie hoch ist die Korrelation zwischen den Items 2 und 3?
ρ(X2, X3) = λ2,1 ∙* λ3,1 + λ2,2 ∙* λ3,2
ρ(X2, X3) = 0.43 ∙* 0.66 + 0.55 ∙ *(-0.23) = 0.157
ρ(X2, X3) = 0.43 ∙* 0.66 + 0.55 ∙ *(-0.23) = 0.157
Bei einer Faktorenanalyse wurden 2 Faktoren extrahiert. Die Ladungen der Faktoren auf den 5 Items lauten folgendermaßen:

Berechnen Sie die Kommunalitäten der Items, bzw. wie viel Varianz der einzelnen Items kann durch die beiden Faktoren erklärt werden?

Berechnen Sie die Kommunalitäten der Items, bzw. wie viel Varianz der einzelnen Items kann durch die beiden Faktoren erklärt werden?
Kommunalitäten der Items, h²i

Wie viel der Varianz im Item i kann durch die extrahierten Faktoren erklärt werden?
h²i ≤ rel(Xi)


Wie viel der Varianz im Item i kann durch die extrahierten Faktoren erklärt werden?
h²i ≤ rel(Xi)

Tags: Berechnung, Faktorenanalyse, Kommunalität
Quelle: Tutorium 3
Quelle: Tutorium 3
Bei einer Faktorenanalyse wurden 2 Faktoren extrahiert. Die Ladungen der Faktoren auf den 5 Items lauten folgendermaßen:

Berechnen Sie die Eigenwerte der Faktoren.

Berechnen Sie die Eigenwerte der Faktoren.
Eigenwerte der Faktoren, Eig(Fj)

Eig(F1) = 0.10² + 0.43² + 0.66² + 0.89² + 0.82² = 2.095
Eig(F2) = 0.88² + 0.55² + (-0.23)² + 0.12² + 0.10² = 1.15

- Wie viel der Gesamtvarianz der Items kann durch den Faktor erklärt werden?
- Mögliche Höhe der Eigenwerte ist abhängig von der Anzahl der Items!!
Eig(F1) = 0.10² + 0.43² + 0.66² + 0.89² + 0.82² = 2.095
Eig(F2) = 0.88² + 0.55² + (-0.23)² + 0.12² + 0.10² = 1.15
Tags: Berechnung, Eigenwert, Faktorenanalyse
Quelle: Tutorium 3
Quelle: Tutorium 3
Berechnen Sie für die beiden Faktoren jeweils den erklärten Anteil
a) an der Gesamtvarianz sowie
b) an der erklärbaren Varianz.
Eig(F1) = 2.095
Eig(F2) = 1.15
Anzahl der Items = 5
a) an der Gesamtvarianz sowie
b) an der erklärbaren Varianz.
Eig(F1) = 2.095
Eig(F2) = 1.15
Anzahl der Items = 5
Berechnung:

Ergebnis:
a)
Faktor 1: 2.095 ∙ 100 / 5 = 42 %
Faktor 2: 1.15 ∙ 100 / 5 = 23 %
b)
Faktor 1: 2.095 ∙ 100 / (2.095 + 1.15) = 0.65 %
Faktor 2: 1.15 ∙ 100 / (2.095 + 1.15) = 0.35 %

Ergebnis:
a)
Faktor 1: 2.095 ∙ 100 / 5 = 42 %
Faktor 2: 1.15 ∙ 100 / 5 = 23 %
b)
Faktor 1: 2.095 ∙ 100 / (2.095 + 1.15) = 0.65 %
Faktor 2: 1.15 ∙ 100 / (2.095 + 1.15) = 0.35 %
Tags: Berechnung, Faktorenrotation
Quelle: Tutorium 3
Quelle: Tutorium 3
Kartensatzinfo:
Autor: coster
Oberthema: Psychologie
Thema: Testtheorie
Schule / Uni: Universität Wien
Ort: Wien
Veröffentlicht: 12.06.2013
Schlagwörter Karten:
Alle Karten (187)
adaptive Testen (1)
adaptiver Test (1)
adaptives Testen (1)
apparativer Test (1)
Axiome (6)
Berechnung (20)
Birnbaum Modelle (1)
Definition (18)
Eigenwert (5)
Erwartungswert (1)
Existenzaxiom (1)
Faktorenanalyse (21)
Faktorenrotation (3)
Faktorenzahl (1)
Faktorwert (1)
Faktorwerte (1)
Fragebogen (2)
Guttman-Skala (4)
Häufigkeit (1)
Hypothese (2)
IRT (32)
Itemanalyse (9)
Itemkonstruktion (3)
Itemtrennschärfe (3)
Itemvarianz (2)
Kennwert (2)
Kennwerte (1)
Kommunalität (2)
Korrelation (3)
Kosten-Nutzen (1)
Kovarianz (1)
Kritik (1)
Ladung (2)
Leistungstest (1)
Likelihood (4)
LLTM (2)
LQT (1)
Marker-Item (1)
Martin Löf Test (1)
Merkmal (3)
Messung (1)
Mittelwert (1)
Modellkontrolle (1)
Modellkontrollen (7)
Normalverteilung (1)
Normierung (4)
Normwerte (5)
Objektivität (5)
Parallelität (1)
Population (2)
projektiver Test (1)
Prozentränge (2)
Rasch-Modell (26)
Regression (1)
Reliabilität (26)
Routineverfahren (2)
Skalenniveau (2)
Skalierung (1)
Spearman-Brown (3)
Stichprobe (1)
Test (8)
Testarten (1)
Testkonstruktion (2)
Tests (1)
Testtheorie (1)
Validität (28)
Varianz (4)
Wissenschaft (2)
z-Test (2)
z-Wert (2)














