Was versteht man unter einer zeitlichen Änderungsrate?
Bei einer zeitlichen Änderungsrate betrachtet man eine (Bestands-)Größe über eine gewisse Zeitdauer.
Verändert sich der Bestand in dieser Zeitspanne, so errechnet man den Änderungsbetrag und teilt diesen durch die Länge der Zeitspanne.
In vielen Fällen wählt man einen Zeitschritt (1 Sekunde, 1 Minute oder 1 Jahr), wodurch der Änderungsbetrag mit der Änderungsrate interpretiert wird. Das ist nicht ganz richtig, da durch die Division mit einer Zeit auch hier die Einheit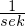 zugefügt werden muss.
zugefügt werden muss.
Verändert sich der Bestand in dieser Zeitspanne, so errechnet man den Änderungsbetrag und teilt diesen durch die Länge der Zeitspanne.
In vielen Fällen wählt man einen Zeitschritt (1 Sekunde, 1 Minute oder 1 Jahr), wodurch der Änderungsbetrag mit der Änderungsrate interpretiert wird. Das ist nicht ganz richtig, da durch die Division mit einer Zeit auch hier die Einheit
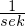 zugefügt werden muss.
zugefügt werden muss.Tags: Änderungsrate
Source:
Source:
Wie lässt sich eine zeitliche Änderungsrate in einem Schaubild veranschaulichen?
Für eine zeitliche Änderungsrate benötigt man zwei "Messpunkte" auf dem Schaubild. Die y-Werte sind hierbei die jeweiligen Bestände, die x-Werte die Zeitpunkte der Messungen.
Verbindet man die beiden Punkte durch eine Gerade (Sekante) und zeichnet zwischen den zwei Punkten das Steigungsdreieck, dann entspricht die Änderungsrate gerade dem Quotienten aus Hochhwert durch Rechtswert - also der Sekantensteigung.
(Je steiler die Sekante, umso größer ist die ÄndR des entsprechenden Bestandes.)
Verbindet man die beiden Punkte durch eine Gerade (Sekante) und zeichnet zwischen den zwei Punkten das Steigungsdreieck, dann entspricht die Änderungsrate gerade dem Quotienten aus Hochhwert durch Rechtswert - also der Sekantensteigung.
(Je steiler die Sekante, umso größer ist die ÄndR des entsprechenden Bestandes.)
Tags: Änderungsrate, Sekante, Sekantensteigung
Source:
Source:
Die Geschwindigkeit lässt sich als zeitliche Änderungsrate auffassen. Begründe!
Trägt man z. B. bei einer Autofahrt die zurückgelegte Strecke über der Zeit in ein Achsenkreuz auf, so kann man mit Hilfe von zwei Punkten des Schaubildes die Durchschnittsgeschwindigkeit zwischen dem entsprechenden Zeitintervall bestimmen.
Sie entspricht der Differenz der Streckenwerte geteilt durch die Dauer des Zeitintervalls - und das ist gerade die mittlere zeitliche ÄndR in diesem Intervall.
Die Steigung einer Sekanten im t-s-Diagramm ist ein Maß für die Geschwindigkeit.
Die zurückgelegte Gesamtstrecke ist hierbei unsere (Bestands-) Größe und die Geschwindigkeit die zeitliche Änderungsrate davon.
Sie entspricht der Differenz der Streckenwerte geteilt durch die Dauer des Zeitintervalls - und das ist gerade die mittlere zeitliche ÄndR in diesem Intervall.
Die Steigung einer Sekanten im t-s-Diagramm ist ein Maß für die Geschwindigkeit.
Die zurückgelegte Gesamtstrecke ist hierbei unsere (Bestands-) Größe und die Geschwindigkeit die zeitliche Änderungsrate davon.
Tags: Änderungsrate, Anwendung
Source:
Source:
Was lässt sich über die Änderungraten von proportionalem und linearem Wachstum aussagen?
Beim proportionalen und linearen Wachstum ist die ÄndR stets konstant.
(Die Sekanten durch zwei Punkte des Schaubildes liegen genau auf dem Schaubild. Ihre Steigung ist immer gleich.)
(Die Sekanten durch zwei Punkte des Schaubildes liegen genau auf dem Schaubild. Ihre Steigung ist immer gleich.)
Tags: Änderungsrate
Source:
Source:
Was weißt du über die Änderungsrate beim exponentiellen Wachstum?
Beim exponentiellen Wachstum ist die ÄndR proportional zum alten Bestand. Mathematisch lässt sich das kurz in Form einer Gleichung darstellen:
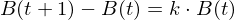 gilt für alle Werte von t.
gilt für alle Werte von t.
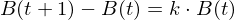 gilt für alle Werte von t.
gilt für alle Werte von t.Tags: Änderungsrate
Source:
Source:
Erstelle je ein t-v-Diagramm zu einer gleichförmigen Bewegung (mit konstanter Geschwindigkeit) und einer gleichförmig beschleunigten Bewegung (konstante Beschleunigung).
Antwort
Bei der Bewegung mit konstanter Geschwindigkeit (blau) ändert sich der "y-Wert" (Geschwindigkeit) nicht. Wir erhalten eine Parallele zur Zeitachse (=x-Achse).
Bei der gleichförmig beschleunigten Bewegung (rot) nimmt die Geschwindigkeit in gleichen Zeitabständen um gleiche Werte zu. Das Schaubild ist eine Ursprungsgerade (bei einer Beschleunigung aus dem Stand.) Die "Steigung" dieser Geraden ist eine Maß für die Änderungsrate der Geschwindigkeit(=Beschleunigung).

Bei der Bewegung mit konstanter Geschwindigkeit (blau) ändert sich der "y-Wert" (Geschwindigkeit) nicht. Wir erhalten eine Parallele zur Zeitachse (=x-Achse).
Bei der gleichförmig beschleunigten Bewegung (rot) nimmt die Geschwindigkeit in gleichen Zeitabständen um gleiche Werte zu. Das Schaubild ist eine Ursprungsgerade (bei einer Beschleunigung aus dem Stand.) Die "Steigung" dieser Geraden ist eine Maß für die Änderungsrate der Geschwindigkeit(=Beschleunigung).
Tags: Änderungsrate, Anwendung
Source:
Source:
Wie bestimmt man die momentane/lokale Änderungsrate einer Funktion f an einer Stelle x (mit der h-Methode)?
Man wählt zu einer Stelle  eine „Nachbarstelle“
eine „Nachbarstelle“ 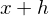 und bildet mit den zugehörigen Funktionswerten
und bildet mit den zugehörigen Funktionswerten 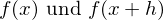 den so genannten Differenzenquotienten
den so genannten Differenzenquotienten 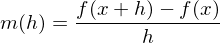
Durch Ausklammern von h im Zähler und durch Kürzen mit h (bzw. geschicktes Umformen) wird der Bruch „reif für den Grenzübergang“: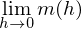 .
.
Nur wenn die Funktionsvariable (x) eine Zeit beschreibt, spricht man von momentaner Änderungsrate. In allen anderen Fällen sagt man lokale Änderungsrate.
Geometrisch entspricht dieser Grenzübergang dem Übergang von einer Sekante zur Tangenten.
Linktipp: Von der Sekanten zur Tangenten
 eine „Nachbarstelle“
eine „Nachbarstelle“ 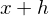 und bildet mit den zugehörigen Funktionswerten
und bildet mit den zugehörigen Funktionswerten 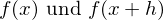 den so genannten Differenzenquotienten
den so genannten Differenzenquotienten 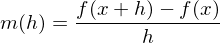
Durch Ausklammern von h im Zähler und durch Kürzen mit h (bzw. geschicktes Umformen) wird der Bruch „reif für den Grenzübergang“:
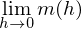 .
.Nur wenn die Funktionsvariable (x) eine Zeit beschreibt, spricht man von momentaner Änderungsrate. In allen anderen Fällen sagt man lokale Änderungsrate.
Geometrisch entspricht dieser Grenzübergang dem Übergang von einer Sekante zur Tangenten.
Linktipp: Von der Sekanten zur Tangenten
Tags: Ableitung, Ableitungsfunktion, Änderungsrate, Begriffe, Differenzenquotient, h-Methode
Source:
Source:
Bestimme die Änderungsrate der Kreisfläche an der Stelle r=4 cm. Handelt es sich um eine lokale oder momentane ÄndR?
Wie groß ist die Änderungsrate an der Stelle r=10 cm?
Wie groß ist die Änderungsrate an der Stelle r=10 cm?
Da die Kreisfläche nicht von der Zeit abhängt, handelt es sich um eine lokale ÄndR.
Bestandsfunktion: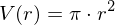
Differenzenquotient: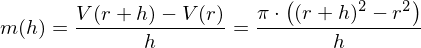
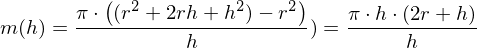
Der Differenzenquotient ist nun "reif für den Grenzübergang", denn nach dem Kürzen mit h kann der Nenner nicht mehr null werden.
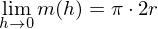
Hieraus folgt für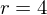 die lokale ÄndR
die lokale ÄndR 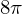 und für
und für 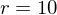 die lokale ÄndR
die lokale ÄndR 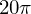 .
.
Bestandsfunktion:
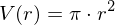
Differenzenquotient:
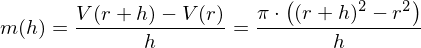
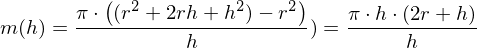
Der Differenzenquotient ist nun "reif für den Grenzübergang", denn nach dem Kürzen mit h kann der Nenner nicht mehr null werden.
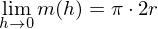
Hieraus folgt für
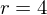 die lokale ÄndR
die lokale ÄndR 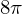 und für
und für 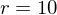 die lokale ÄndR
die lokale ÄndR 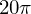 .
.Tags: Ableitung, Ableitungsfunktion, Änderungsrate, Begriffe, Differenzenquotient, h-Methode
Source:
Source:
Flashcard set info:
Author: www.mathematik-bw.de
Main topic: Mathematik
Topic: 10. Klasse
School / Univ.: Clara-Schumann-Gymnasium
City: Lahr
Published: 23.12.2009
Card tags:
All cards (47)
Ableitung (10)
Änderungsrate (9)
Anwendung (2)
Begriffe (17)
Definitionsmenge (1)
Extremstelle (2)
Funktion (8)
ganzrational (5)
Gerade (13)
Grad (1)
h-Methode (6)
hinreichend (3)
Intervalle (1)
Normale (2)
notwendig (2)
Nullstelle (5)
Produktform (3)
Sattelpunkt (3)
Schnittwinkel (1)
Sekante (1)
Sekantensteigung (1)
Steigungswinkel (3)
Streckung (1)
Symmetrie (3)
Tangente (7)
Terassenpunkt (3)
Verschiebung (7)
Wertemenge (1)



