Hol' Dir diese Lernkarten, lerne & bestehe Prüfungen. Kostenlos! Auch auf iPhone/Android!

Die mathematische Herausforderung im Rahmen der Faktorenanalyse ist die Bestimmung der (unbekannten) Ladungen sowie die Festlegung der Faktorenzahl.

Die Grundidee der Parameterschätzung basiert darauf, zunächst jenen Faktor mit dem größten Eigenwert zu „extrahieren“. Dadurch wird die Summe der quadrierten verbleibenden Korrelationen zwischen den Items am stärksten minimiert.

Daraus folgt, dass man die Ladungen des 1. Faktors so bestimmt, dass


Die mathematische Name dieses Problems nennt sich „Eigenwert – Eigenvektor Problem“ und wurde (zum Glück) bereits gelöst.
Der Lösungsweg erfolgt iterativ und ist in realen Situationen für die händische Berechnung viel zu aufwändig.

Nach Extraktion des ersten Faktors (= Schätzung der Ladungen des ersten Faktors), wird der zweite Faktor nach derselben Grundidee extrahiert. Allerdings verwendet man hierfür nicht die originalen Korrelationen, sondern die um den Einfluss des ersten Faktors reduzierten. Diese Korrelationen werden „Restkorrelationen“ genannt.

Im Rahmen der Faktorenanalyse wurden eine Vielzahl an Extraktionsverfahren entwickelt. Die zwei am häufigsten angewandten sind
– die Hauptachsenanalyse („principal axis“) und
– die Hauptkomponentenanalyse („principal components“).

Bei der Hauptkomponentenanalyse wird davon ausgegangen, dass sich die Varianz eines Items vollständig durch die gemeinsamen Faktoren erklären lässt. Demnach sind alle Kommunalitäten (und somit auch die Korrelationen eines Items mit sich selbst) gleich 1. Als Konsequenz werden so viele Faktoren extrahiert, wie es Items gibt.
Sie ist die Standardeinstellung bei Berechnung einer Faktorenanalyse in SPSS.

Bei der Hauptachsenanalyse wird davon ausgegangen, dass sich die Varianz eines Items immer in die Kommunalität und die Einzelrestvarianz aufteilt. Demnach sind die Kommunalitäten (und somit auch die Korrelationen eines Items mit sich selbst) kleiner als 1.
Ziel ist es also, nur die durch die gemeinsamen Faktoren erklärbare Varianz zu beschreiben.
Da zu Beginn der Datenanalyse die Kommunalitäten nicht bekannt sind (=„Kommunalitätenproblem“), werden die Faktoren zunächst mittels Hauptkomponentenanalyse geschätzt und iterativ (=schrittweise) „verbessert“ („Kommunalitäteniteration“).
Kommunalitätenproblem - Vorgehensweise:
- „1“ wird in die Hauptdiagnoale geschrieben (jedes Items mit sich selbst)
- Mit der Lösung erhält man (etwas falsche) Ladungen
- Durch diese Ladungen erhält man (falsche) Kommunalitäten.
- Diese setzt man dann wiederrum in die Hauptdiagonale ein und führt die gesamte Berechnung neu durch.
- Dadurch kommt man zu immer besseren Daten.

Laut Backhaus et al.* unterscheidet sich die Interpretation der Faktoren je nach Methode.
Bei der Hauptkomponentenanalyse geht es darum, die hoch auf einem Faktor ladenden Items zu einem Sammelbegriff zusammenzufassen.
Bei der Hauptachsenanalyse geht es darum, die „Ursachen“ für die (hohen) Korrelationen zwischen den Items zu finden.

Mathematisch sind dies 2 leicht verschiedene Modelle, dies ist aber nicht weiter zu beachten (State of the art – in der Literatur wird immer die Hauptachsenanalyse erklärt – aber bei SPSS mit der Hauptkomponentenanalyse berechnet.

Für die Bestimmung der Anzahl an Faktoren gibt es fünf üblicherweise herangezogene Kriterien

• Faktorenzahl wird a priori festgelegt
• alle Restkorrelationen sind nahe 0 (z.B.: <.2)
• der Eigenwert des zuletzt extrahierten Faktors ist kleiner 1* (auch "Kaiser-Kriterium": im übertragenen Sinn ist damit die „Information, die über den Faktor vorliegt“ geringer als die Information eines einzigen Items),
Ein Item hat die Varianz 1; wenn ein Faktor einen Eigenwert von weniger als 1 hat, dann enthält der Faktor weniger Information als ein einziges Item. Es macht dann keinen Sinn diesen Faktor zu verwenden.
• der Verlauf des Eigenwertediagramms (Screeplot)
Bei der Betrachtung des Eigenwertediagramms, wird jene Stelle gesucht, an der Verlauf das Eigenwertediagramm „abflacht“ (= Elbow Kriterium). Die Faktoren vor dem „Knick“ werden in der weiteren Analyse berücksichtigt.
• die Parallelanalyse
Bei der Parallelanalyse werden zumindest 100 Datensätze von Zufallszahlen erzeugt, wobei die Anzahl an Items und der Stichprobenumfang dem empirisch gewonnenen Datensatz entspricht. All diese Datensätze werden einer Faktorenanalyse unterzogen und die aus jeder Analyse gewonnenen Eigenwerte werden pro Faktor gemittelt. Als relevante nichttriviale Faktoren werden all jene Faktoren bezeichnet, deren Eigenwerte über jenen der (gemittelten) Eigenwerte der Parallelanalyse liegen.Dort wo die Parallelanalyse (zufällige Werte) die realen Eigenwerte schneidet, dort liegt die Grenze. PROBLEM: sehr aufwändig.

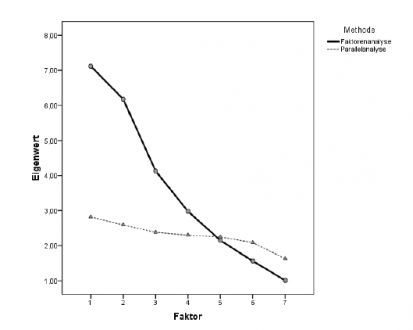
Für die Bestimmung der Faktorenzahl gibt es keine generellen Vorschriften, sodass der Grad an Subjektivität hier relativ hoch ist.

Die Ladungsmatrix bildet die Grundlage für die inhaltliche Interpretation der Faktoren. Hierfür werden üblicherweise die in einem Faktor hoch (=ideal sind Items mit Ladungen über 0.7) und in allen anderen Faktoren niedrig ladenden Items (ideal sind hier Ladungen unter 0.3) herangezogen. Diese Items werden auch als „Marker-Items“ bezeichnet.
Zeichnet man die Items als Punkte in einem Raum mit so vielen Dimensionen wie es Faktoren gibt, so liegen „Marker-Items“ „nahe“ an den Koordinatenachsen.

Vorgehen:
- Man nimmt Items die in einem Faktor hoch laden = Marker-Items
- Diese sollten im Idealfall in anderen Items niedrig laden.
- Bei diesen Items sollte man die Eigenschaft dann gut erkennen.

Wegen der Vorgehensweise bei der Parameterschätzung sind derartig hohe Ladungen bei der „Erstlösung“ in der Praxis aber eher selten.
Aus diesem Grund werden die Faktoren zur besseren Interpretierbarkeit „rotiert“.

Ziel ist eine einfache Struktur („simple structure“) bei der jedes Item nach Möglichkeit nur in einem Faktor hoch in den anderen Faktoren jedoch gering lädt.
Dadurch ergeben sich neue, besser interpretierbare Ladungen.

Die Schätzung der unbekannten Parameter erfolgt im Rasch Modell üblicherweise mit Hilfe der Maximum-Likelihood-Methode.
Hierbei werden die unbekannten Parameter so geschätzt, dass die Likelihood der Daten maximal wird.

Die Parameterschätzung benötigt man für die Schätzung der Personenfähigkeit bzw. der Itemschwierigkeit.

Probleme bei der Parameterschätzung ergeben sich, wenn es kein eindeutig definiertes Maximum der Likelihoodfunktion gibt.
Dies ist der Fall, wenn die Funktion

• multiple Maxima hat (d.h. es neben den globalen noch lokale Maxima gibt) oder
• das Maximum kein Punkt, sondern ein Plateau oder eine Fläche ist.

Die Genauigkeit der Schätzung hängt davon ab, wie viel Information man über einen Parameter besitzt.

Die Genauigkeit der Parameterschätzung der Personenfähigkeit kann erhöht werden durch die zusätzliche Abfrage von Items mit einer Itemschwierigkeit die der aktuellen Personenfähigkeit entsprechen (da diese Items die Person mit einer Wahrscheinlichkeit von 50% löst).

Die Information = Die Wahrscheinlichkeit dass das Ereignis eintritt mal der Wahrscheinlichkeit dass das Ereignis nicht eintritt.

Je ähnlicher die Schwierigkeit eines Items i der Fähigkeit einer Person v ist, umso höher ist die Information, die eine Person über ein Item bzw. ein Item über eine Person liefert.
Die Genauigkeit der Parameterschätzung der Personenfähigkeit kann erhöht werden durch die zusätzliche Abfrage von Items mit einer Itemschwierigkeit die der aktuellen Personenfähigkeit entsprechen (da diese Items die Person mit einer Wahrscheinlichkeit von 50% löst).


Je größer die Information, die man über ein Item bzw. über eine Person sammelt, umso genauer kann man den Item bzw.
Personenparameter schätzen.

Daraus folgt:
Hat man einen fixen Test, so ist die Messgenauigkeit dieses Tests nicht bei allen Personen gleich.
Für die Items gilt: je stärker die Itemschwierigkeit von der durchschnittlichen Personenfähigkeit einer Gruppe abweicht umso ungenauer ist die Schätzung der Itemschwierigkeit.

Bei einem fixen Test ist die Messgenauigkeit nicht bei allen Personen gleich, denn je besser die Personenfähigkeit zur Itemschwierigkeit passt, desto besser kann man die Personenfähigkeit schätzen.