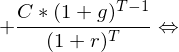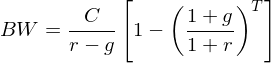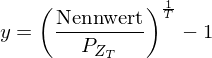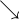Methodologie im Bereich Finanzwirtschaft


Quantitative Lösungen für komplexe Probleme.
| Anwendung eines zweistufigen Entscheidungsprozesses: |
| Ausdrücken aller Konsequenzen einer Entscheidung in Zahlungen |
| Aggregation aller Zahlungen. |
| Dieser Entscheidungsprozess heißt typischerweise “Bewertung”. |
Tags: bewertung, methodologie
Source: IuF Teil 1, Folie 3
Source: IuF Teil 1, Folie 3
Definition: Investition/Finanzierung


Investition: Entscheidung, die zunächst eine Auszahlung zur Folge
hat.
Finanzierung: Entscheidung, die zunächst eine Einzahlung zur Folge
hat.
hat.
Finanzierung: Entscheidung, die zunächst eine Einzahlung zur Folge
hat.
Tags: finanzierung, investition
Source: IuF Teil 1, Folie 4
Source: IuF Teil 1, Folie 4
Finanzwirtschaftliche Sicht des Unternehmens


| Vermögenswerte | % | % | Verbindlichkeiten |
| Wert der Zahlungen der bestehenden Investitionen | Kurz- und langfristige Vermögenswerte | Fremdkapital | Anspruch auf fixe Zahlungen, Geringe oder gar keine Rolle in der Unternehmensführung, Fixe Fälligkeit, Steuerabzugsfähigkeit |
| Erwarteter Wert der Zahlungen zukünftiger Investitionen | Zukünftige Vermögenswerte | Eigenkapital | Residualanspruch auf die Zahlungen, Bedeutende Rolle in der Unternehmensführung, Unendliche Lebensdauer |
Tags: verbindlichkeiten, vermögenswerte
Source: IuF Teil 1, Folie 5
Source: IuF Teil 1, Folie 5
Wertschöfpung durch geschickte Investitionen


Implementierung von Projekten, deren Ertrag die Kosten der
Finanzierung übersteigt.
Entscheidung gegen Projekte, deren Ertrag die Kosten der
Finanzierung unterschreitet.
Finanzierung übersteigt.
Entscheidung gegen Projekte, deren Ertrag die Kosten der
Finanzierung unterschreitet.
Tags: investition, wertschöfpung
Source: IuF Teil 1, Folie 6
Source: IuF Teil 1, Folie 6
Finanzierungsarten: EK vs FK


Eine Unternehmung finanziert sich typischerweise mit Eigen- und
Fremdkapital.
Fremdkapital.
| Das grundsätzliche Unterscheidungsmerkmal zwischen Eigen- und Fremdkapital ist die Rechtsstellung der Kapitalgeber. |
| Bei Fremdkapital ist der Kapitalgeber Gläubiger und eine Verletzung der vertraglichen Verpflichtungen hat insolvenzrechtliche Konsequenzen. |
| Im Vergleich zu Ansprüchen von Eigentümern sind diejenigen von Gläubigern im Insolvenzrecht vorrangig. |
| Typischerweise werden in Fremdkapitalverträgen konkrete Zahlungsvereinbarungen getroffen. |
| Typische Finanzierungsarten | % |
| Eigenkapital | Nicht-ausgeschüttete Zahlungsüberschüsse, Aktien (bei Aktiengesellschaften), Stammanteile (bei GmbH). |
| Fremdkapital | Kredite, Schuldverschreibungen (Anleihen). |
Tags: eigenkapital, fremdkapital
Source: IuF Teil 1, Folie 8
Source: IuF Teil 1, Folie 8
Aktien (1/2)


Das Grundkapital einer Aktiengesellschaft wird in Aktien aufgeteilt
und bildet typischerweise den Löwenanteil des Eigenkapitals.
Aktien besitzen keine begrenzte Laufzeit
Aktien können an Börsen gehandelt werden
und bildet typischerweise den Löwenanteil des Eigenkapitals.
| Aktien verbriefen im Grundsatz folgende Rechte |
| Recht auf Anteil am Bilanzgewinn (in Form einer Dividende) |
| Recht auf Anteil am Liquidationserlös. |
| Teilnahme an, Rederecht und Stimmrecht auf der Hauptversammlung. |
| Auskunftsrecht |
| Recht zur Stellung von Anträgen. |
| Recht zum Bezug junger Aktien. |
Aktien besitzen keine begrenzte Laufzeit
Aktien können an Börsen gehandelt werden
Tags: aktie, aktien
Source: IuF Teil 1, Folie 9
Source: IuF Teil 1, Folie 9
Akiten (2/2)


| Wichtige Unterscheidung: Stammaktien versus Vorzugsaktien. |
| Vorzugsaktien gewähren dem Inhaber bestimmte Vorrechte gegenüber Stammaktien |
| Typisch sind ein besonderer Dividendenanspruch (z.B. Vorab- oder Überdividende) gepaart mit der Abwesenheit des Stimmrechts. |
| Es existieren aber auch andere Formen von Vorzugsaktien, z.B. Mehrstimmrechtsaktien. |
| Eine Kapitalerhöhung bei einer Aktiengesellschaft erfolgt typischerweise durch die Ausgabe junger Aktien (Alternative: Kapitalerhöhung aus Gesellschaftsmitteln). | |
| Eine Kapitalerhöhung muss von der Hauptversammlung (HV) mit mindestens Drei-Viertel-Mehrheit des vertretenen Grundkapitals beschlossen werden. | |
| Eine Kapitalerhöhung kann auch im Vorhinein von der HV genehmigt werden. Allgemein: genehmigtes Kapital; mit aufschiebender Bedingung: bedingtes Kapital. |
Tags: aktie, aktien, stammaktien, vorzugsaktien
Source: IuF Teil 1, Folie 10
Source: IuF Teil 1, Folie 10
Definition: Kreditfinanzierung


| Ein Kredit ist die Gebrauchsüberlassung von Geld (oder vertretbaren Sachen) auf Zeit. |
| Als Kompensation für den Kreditgeber wird ein Kreditzins vereinbart. Dieser ist abhängig von der Bonität des Kreditnehmers. |
| Kredite an Unternehmen sind häufig besichert. |
| Kreditverträge enthalten typischerweise Zusatzvereinbarungen (Covenants) mit Auflagen für den Kreditnehmer. |
Tags: covenants, kreditfinanzierung
Source: IuF Teil 1, Folie 11
Source: IuF Teil 1, Folie 11
Wichtige Kreditarten (1/2)


| Kontokorrentkredit (Kreditlinie) | |
| Zur Abwicklung des operativen Geschäfts | |
| Hat fixe oder unbestimmte Laufzeit. | |
| Ist ein revolvierender Kredit: Kann nach zwischenzeitlicher Rückführung immer wieder neu in Anspruch genommen werden. | |
| Für den nicht in Anspruch genommenen Teil fällt eine Bereitstellungsprovision an. | |
| Typischerweise ist der vereinbarte Zinssatz recht hoch |
Lieferantenkredit durch die Vereinbarung von Zahlungszielen.
Tags: kontokorrentkredit, kreditarten, kreditlinie, lieferantenkredit
Source: IuF Teil 1, Folie 13
Source: IuF Teil 1, Folie 13
Wichtige Kreditarten (2/2)


Langfristige Kredite
| Tilgungsformen |
| Endfällige Darlehen: Gesamttilgung am Ende der Laufzeit |
| Tilgungsdarlehen: Konstanter Tilgungsbetrag je Periode; impliziert rückläufige Gesamtzahlung. |
| Annuitätendarlehen: Im Zeitablauf ansteigende Tilgungsbeträge, so dass die Gesamtzahlung konstant bleibt |
| Zinsformen |
| Fester Zinssatz |
| Variabler Zinssatz. Typischerweise geknüpft an einen generellen |
| Marktzinssatz, z.B. LIBOR oder EURIBOR (London bzw. European Interbank Offered Rate). |
Tags: kreditarten, langfristige kredite, tilgungsformen, zinsformen
Source: IuF Teil 1, Folie 14
Source: IuF Teil 1, Folie 14
Finanzierung durch Schuldverschreibungen


| Schuldverschreibungen sind den Krediten ähnlich, allerdings werden die Ansprüche gegenüber dem Schuldner verbrieft. |
| Dies macht gerade Inhaberpapiere sehr leicht handelbar. |
| Typische Schuldverschreibungen sind Industrieanleihen (längerfristig) oder Commercial Paper (kurzfristig, unbesichert, Ausgabe im Rahmen eines Emissionsprogramms). |
| Es existieren außer reinen Schuldpapieren auch Anleihen mit teilweisem Eigenkapitalcharakter (z.B. Wandelanleihen). |
Tags: commercial paper, finanzierung, industrieanleihe, schuldverschreibungen, wandelanleihe
Source: IuF Teil 1, Folie 15
Source: IuF Teil 1, Folie 15
Kernprinzipien der Finanzwirtschaft
Vorbemerkung: Typischerweise wird unterstellt, dass Menschen in ihrem eigenen besten Interesse handeln (rational)

Vorbemerkung: Typischerweise wird unterstellt, dass Menschen in ihrem eigenen besten Interesse handeln (rational)

Kernprinzipien:
| 1. Primat der Zahlungen | Für eine Entscheidung sind allein Zahlungen (oder Zahlungsäquivalente) relevant. |
| 2. Zeitwert des Geldes | Der Wert einer Zahlung hängt davon ab, wann sie erfolgt. |
| 3. Ertrag vs. Risiko | Bei vielen Entscheidungen ist eine Abwägung zwischen Ertrag und Risiko zu treffen. |
| 4. Aggregation durch Märkte | Wertpapiermärkte aggregieren Präferenzen und Informationen. |
| 5. Arbitragefreiheit | Preise an kompetitiven Wertpapiermärkten zeichnen sich durch die Abwesenheit von Arbitrage aus. |
Tags: finanzwirtschaft, kernprinzipien
Source: IuF Teil 1, Folie 16
Source: IuF Teil 1, Folie 16
Kernprinzipien: Details (1/2)


| Erträge, Gewinne, etc. bleiben so lange fiktiv, bis sie sich in Zahlungen umsetzen. |
| Je früher eine Zahlung gegebener Höhe anfällt, desto wertvoller ist sie. Dies liegt unter anderem daran, dass eine frühere Zahlung höhere Wiederanlageerträge erbringt. |
| Die wenigsten Zahlungen aus Investitionen sind sicher. |
| Da Menschen typischerweise risikoavers sind, bewerten sie stärker mit Risiko behaftete Zahlungen ceteris paribus geringer. |
Tags: kernprinzipien
Source: IuF Teil 1, Folie 17
Source: IuF Teil 1, Folie 17
Kernprinzipien: Details (2/2)


| Die effektive Aggregation von Präferenzen durch Märkte ist ein zentrales Element der marktwirtschaftlichen Ordnung. |
| Märkte funktionieren nur dann gut, wenn sie kompetitiv sind. |
| In kompetitiven Märkten für riskante Wertpapiere ergibt sich dadurch ein “Preis für Risiko”. |
| Kompetitive Wertpapiermärkte aggregieren auch Informationen über die Qualität von Wertpapieren. |
| Wenn die Informationsaggregation in idealer Weise verläuft, spricht man von einem effizienten Markt. |
| Effiziente Märkte haben damit auch weitreichende Steuerungswirkungen. |
Tags: kernprinzipien
Source: IuF Teil 1, Folie 18
Source: IuF Teil 1, Folie 18
Tags: einperiodige verzinsung, endwert
Source: IuF Teil 2, Folie 3
Source: IuF Teil 2, Folie 3
Tags: Barwert, Einperiodige Verzinsung
Source: IuF Teil 2, Folie 4
Source: IuF Teil 2, Folie 4
Tags: Endwert, Mehrperiodige Verzinsung
Source: IuF Teil 2, Folie 6
Source: IuF Teil 2, Folie 6
Tags: Barwert, Mehrperiodige Verzinsung
Source: IuF Teil 2, Folie 5
Source: IuF Teil 2, Folie 5
Unterjährige Verzinsung: Endwert


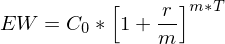
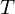 | Investitionshorizont in Jahren
| Investitionshorizont in Jahren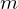 | Anzahl der unterjährigen Verzinsungen
| Anzahl der unterjährigen VerzinsungenTags: Endwert, Unterjährige Verzinsung
Source: IuF Teil 2, Folie 9
Source: IuF Teil 2, Folie 9
Unterjährige Verzinsung: Effektiver Jahreszinssatz (1/2)


| Bei unterjähriger Verzinsung verzinst sich das Investment effektiv zu einem anderen Zinssatz als dem angegebenen Jahreszinssatz (in diesem Fall auch als nominaler Jahreszinssatz bezeichnet), da ein Zinseszinseffekt innerhalb eines Jahres zusätzlich zum jährlichen Zinseszinseffekt existiert. | |
| Dieser Zinssatz wird effektiver Jahresszinssatz genannt. | |
| Er ist identisch mit dem jährlichen Zinssatz, bei dem derselbe Endwert nach demselben Investitionshorizont von T Perioden durch die jährliche Verzinsung derselben Investitionssumme entsteht. |
Tags: Effektiver Jahreszinssatz, Unterjährige Verzinsung
Source: IuF Teil 2, Folie 10
Source: IuF Teil 2, Folie 10
Unterjährige Verzinsung: Effektiver Jahreszinssatz (2/2)
Damit ergibt sich
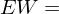
also
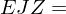
Damit ergibt sich
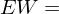
also
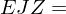
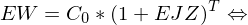
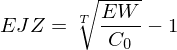
EW entspricht hier dem EW, der zuvor mit der unterjährigen Verzinsung ausgerechnet wurde
Tags: Effektiver Jahreszinssatz, Unterjährige Verzinsung
Source: IuF Teil 2, Folie 11
Source: IuF Teil 2, Folie 11
Stetige Verzinsung


Die stetige Verzinsung ist ein Spezialfall der unterjährigen Verzinsung, bei dem für eine jede infinitesimal kleine Zeiteinheit die Verzinsung stattfindet.
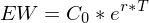
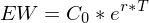
Tags: Stetige Verzinsung
Source: IuF Teil 2, Folie 12
Source: IuF Teil 2, Folie 12
Mehrperiodige Zahlungsströme: Barwert 1/2


Die Summe der Barwerte jeder einzelnen Zahlung 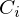 pro Periode
pro Periode  ergibt den Barwert
ergibt den Barwert 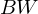 des gesamten Zahlungsstroms, wobei
des gesamten Zahlungsstroms, wobei 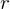 den Zinssatz pro Periode darstellt.
den Zinssatz pro Periode darstellt.
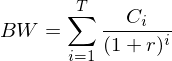
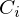 pro Periode
pro Periode  ergibt den Barwert
ergibt den Barwert 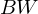 des gesamten Zahlungsstroms, wobei
des gesamten Zahlungsstroms, wobei 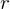 den Zinssatz pro Periode darstellt.
den Zinssatz pro Periode darstellt.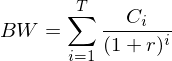
Tags: Barwert, Mehrperiodige Zahlungsströme
Source: IuF Teil 2, Folie 13
Source: IuF Teil 2, Folie 13
Tags: Barwert, Mehrperiodige Zahlungsströme
Source: IuF Teil 2, Folie 14
Source: IuF Teil 2, Folie 14
Tags: Endwert, Mehrperiodige Zahlungsströme
Source: IuF Teil 2, Folie 16
Source: IuF Teil 2, Folie 16
Kapitalwert einer Investition


Der Kapitalwert KW (Net Present Value, NPV) einer Investition ist die Summe der Barwerte 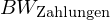 der zukünftigen, mit der Investition verbundenen Zahlungen (ohne die Anfangsauszahlung der Investition) abzüglich der Anfangsauszahlung zur Initialisierung der Investition bei einem Investitionshorizont von
der zukünftigen, mit der Investition verbundenen Zahlungen (ohne die Anfangsauszahlung der Investition) abzüglich der Anfangsauszahlung zur Initialisierung der Investition bei einem Investitionshorizont von 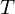 Perioden:
Perioden:
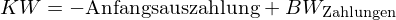
Entscheidungsregel: Ist der Kapitelwert positiv, lohnt sich eine Investition
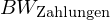 der zukünftigen, mit der Investition verbundenen Zahlungen (ohne die Anfangsauszahlung der Investition) abzüglich der Anfangsauszahlung zur Initialisierung der Investition bei einem Investitionshorizont von
der zukünftigen, mit der Investition verbundenen Zahlungen (ohne die Anfangsauszahlung der Investition) abzüglich der Anfangsauszahlung zur Initialisierung der Investition bei einem Investitionshorizont von 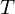 Perioden:
Perioden: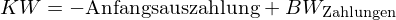
Entscheidungsregel: Ist der Kapitelwert positiv, lohnt sich eine Investition
Tags: investition, kapitalwert
Source: IuF Teil 2, Folie 17
Source: IuF Teil 2, Folie 17
Tags: Ewige Rente, Rentenformeln
Source: IuF Teil 2, Folie 20
Source: IuF Teil 2, Folie 20
Tags: Endliche Rente, Rentenformeln
Source: IuF Teil 2, Folie 23
Source: IuF Teil 2, Folie 23
Tags: Ewige Rente mit konstantem Wachstum, Rentenformeln
Source: IuF Teil 2, Folie 27
Source: IuF Teil 2, Folie 27
Tags: Endliche Rente mit konstantem Wachstum, Rentenformeln
Source: IuF Teil 2, Folie 29
Source: IuF Teil 2, Folie 29
Fazit


| Der Wert zukünftiger Zahlungen wird im Barwert bzw. Endwert verdichtet, indem sie mit einem Zinssatz auf den gegenwärtigen Zeitpunkt bzw. letzten Zahlungszeitpunkt diskontiert bzw. aufgezinst werden. | |
| Der Kapitalwert einer Investition ist der Barwert derer Zahlungen abzüglich der Anfangsauszahlung. | |
| Rentenformeln minimieren den Aufwand zur Berechnung spezieller Zahlungsströme. |
Tags: abzinsen, aufzinsen, barwert, endwert, fazit, kapitalwert, rentenformeln
Source: IuF Teil 2, Folie 31
Source: IuF Teil 2, Folie 31
Methoden der Investitionsentscheidung / Capital Budgeting


| Als Capital Budgeting wird der Entscheidungsprozess über die Durchführung von Investitionen bezeichnet. |
| Zur Unterstützung des Entscheidungsprozesses dienen folgende Methoden: |
| Kapitalwertmethode |
| Methode der Kapitalwertrate |
| Amortisationsrechnung |
| Rentabilitatsrechnung |
| Interne Zinssatzmethode |
Tags: capital budgeting, investitionsentscheidung
Source: IuF Teil 3, Folie 2
Source: IuF Teil 3, Folie 2
Kapitalwert einer Investition


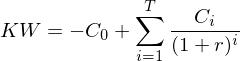
Der Zinssatz pro Periode, der in die Barwertberechnung eingeht,
bestimmt sich nach der Rendite pro Periode, für die ein bestimmtes Risiko, welches mit einer Investition unter Unsicherheit einhergeht, erwartet wird.
Diese erwartete risikoadjustierte Rendite kann sich an den
Opportunitatskosten fur das in der Investition gebundene Kapital orientieren und wird auch als Kapitalkostensatz bezeichnet.
Tags: kapitalkostensatz, kapitalwert
Source: IuF Teil 3, Folie 3
Source: IuF Teil 3, Folie 3
Kapitalwertmethode


| Entscheidungsregel der Kapitalwertmethode: Führe die Investition durch, wenn deren Kapitalwert positiv ist. | |
| In diesem Fall verdient das Projekt mindestens alle mit ihm verbundenen Auszahlungen und weist mindestens die erwartete riskoadjustierte Rendite pro Periode auf. |
Tags: kapitalwertmethode
Source: IuF Teil 3, Folie 4
Source: IuF Teil 3, Folie 4
Kapitalwertmethode: Diskussion


| Vorteile der Kapitalwertmethode: |
| Cashflows als Grundlage |
| Mehrperiodizitat |
| Berücksichtigung erwarterter risikoadjustierter Renditen |
| Es existiert folgendes Problem: |
| Ist das einzusetzende Kapital knapp und infolgedessen können nicht alle Projekte mit positivem Kapitalwert durchgeführt werden, liefert die Kapitalwertmethode keine Lösung des Auswahlproblems. |
| Lösunsmöglichkeit: Methode der Kapitalwertrate |
Tags: kapitalwertmethode, kapitalwertrate
Source: IuF Teil 3, Folie 5
Source: IuF Teil 3, Folie 5
Methode der Kapitalwertrate 1/3


Die Kapitalwertrate KWR (Profitability Index) wird definiert als Quotient aus dem Barwert der mit der Investition verbundenen Auszahlungen (ohne die Anfangsauszahlung) und der Anfangsauszahlung:
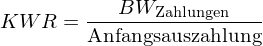
KWR bei Projekt 3:
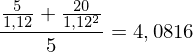
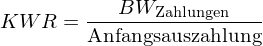
KWR bei Projekt 3:
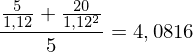
Tags: kapitalwertrate
Source: IuF Teil3, Folie 6
Source: IuF Teil3, Folie 6
Methode der Kapitalwertrate 2/3


| Entscheidungsregel bei unabhängigen Projekten: Führe ein Projekt durch, wenn dessen Kapitalwertrate größer als 1 ist. | |
| Danach können alle drei Projekte durchgeführt werden, wenn die Projekte voneinander unabhangig sind. |
Tags: kapitalwertrate
Source: IuF Teil 3, Folie 7
Source: IuF Teil 3, Folie 7
Methode der Kapitalwertrate 3/3


| Wenn das Kapital, welches in Form der Anfangsauszahlungen an alle unabhängigen Projekte zum Zeitpunkt 0 insgesamt investiert werden soll, nicht für die Anfangsauszahlungen aller Projekte ausreicht, werden die Projekte nach ihrer Kapitalwertrate absteigend priorisiert und nacheinander ausgewählt, solange das Kapital für das aktuell betrachtete und alle vorher selektierten Projekte ausreichend ist. Die Kapitalwertmethode hingegen kann in einem solchen Fall kein optimales Ergebnis liefern. |
| Wichtige Einschränkung: Die Methode funktioniert nur im Falle eines limitierten Kapitals für die Anfangsauszahlungen zum Zeitpunkt 0. |
| Im Beispiel bei einem maximal zur Verfügung stehenden Kapital von 10 Millionen werden demnach die Projekte 2 und 3 ausgewählt. |
Tags: kapitalwertrate
Source: IuF Teil 3, Folie 8
Source: IuF Teil 3, Folie 8
Methode der Kapitalwertrate: Problem


| Der Grund liegt in der unterschiedlichen Größenordnung der Anfangsauszahlungen beider Projekte, da die Kapitalwertrate Größenunterschiede nicht berücksichtigt. | |
| Lösungsmöglichkeit des Problems: Betrachtung der durch das Projekt 1 zusätzlich zu Projekt 2 generierten Zahlungen als ein eigenes Projekt. Weist dieses Projekt eine Kapitalwertrate größer als 1 auf, ist Projekt 1 dem Projekt 2 vorzuziehen, wie es hier der Fall ist: |
| 1-2 | 5 | 15 | 0 | 13,3929 | 2,6786 | 8,3929 |
Tags: kapitalwertrate
Source: IuF Teil 3, Folie 9
Source: IuF Teil 3, Folie 9
Amortisationsrechnung


Bei der Amortisationsrechnung (Payback Method) wird die Zeitspanne bestimmt, in der die Anfangsauszahlung (= 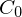 ) eines Investitionsprojektes wieder in Form der durch das Projekt verbundenen kumulierten Zahlungen zürückgeflossen ist. ) eines Investitionsprojektes wieder in Form der durch das Projekt verbundenen kumulierten Zahlungen zürückgeflossen ist. | |
| Für drei Projekte mit einem jeweiligen Horizont von 4 Jahren und folgenden Zahlungsströmen ergeben sich demnach die als Amortisationsdauer bezeichneten Zeitspannen AD: 3,3,3 | |
| Entscheidungsregel: Führe die Investitionsprojekte durch, die eine bestimmte maximale Amortisationsdauer aufweisen. | |
| Bei einer gewünschten Amortisationsdauer von 3 Jahren sind demnach alle drei Projekte durchzuführen. |
Tags: amortisationsdauer, amortisationsrechnung
Source: IuF Teil 3, Folie 10
Source: IuF Teil 3, Folie 10
Amortisationsrechnung: Diskussion 1/2


| Vorteile der Amortisationsrechnung | |
| Schnell und einfach anzuwendende Methode, besonders bei operational häufig auftretenden Enscheidungssituationen kleinerer Größenordnung. | |
| Dient zur Managementbewertung in der Weise, dass Fehleinschätzungen des Managements in der Prognose des Zahlungsstroms mit Erreichen der Periode der gewünschten Amortisationsdauer offenbart werden, wenn zu diesem Zeitpunkt die kumulierten Zahlungen nicht die Anfangsauszahlung erreichen. | |
| Besondere Eignung für Firmen, die keinen guten Zugang zu apitalmärkten haben und durch diese Methode steuern können, dass ein schneller Kapitalrückfluss durch die Investitionsprojekte erreicht wird und sich so bessere Reinvestitionsmöglichkeiten eröffnen. |
Tags: amortisationsrechnung
Source: IuF Teil 3, Folie 11
Source: IuF Teil 3, Folie 11
Amortisationsrechnung: Diskussion 2/2


| Probleme bei der Amortisationsrechnung: | |
| Keine Berücksichtigung des Zeitpunktes der Zahlungen, also der Präferenz von früheren gegenüber späteren Zahlungen: Im Beispiel werden Projekt 1 und 2 als gleichwertig nach der Amortisationsdauer gewertet, obwohl der Kapitalwert von Projekt 2 wegen seiner größeren anfänglichen Zahlungen den Kapitalwert des Projektes 1 (bei positivem Zinssatz) übertrifft. | |
| Lösungsmöglichkeit: Betrachtung der Barwerte aller Zahlungen anstatt der Zahlungen selbst bei der Bestimmung der Amortisationsdauer | |
| Keine Berücksichtigung von Zahlungen nach der Amortisationsdauer: Projekt 3 hat denselben Rang wie Projekt 2, obwohl nach der Amortisationsdauer im vierten Jahr Projekt 3 eine viel größere Zahlung aufweist. | |
| Willkürliche Bestimmung der gewünschten Amortisationsdauer. |
Tags: amortisationsdauer, amortisationsrechnung
Source: IuF Teil 3, Folie 12
Source: IuF Teil 3, Folie 12
Rentabilitätsrechnung


Rentabilitätskennzahlen als Ergebnis der Rentabilitätsrechnung setzen beispielweise in Form der Kapitalrentabilität KR eine Ergebnisgröße E ins Verhältnis zu einer Kapitalgröße K:
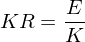
Dabei ist auf die Konsistenz der beiden Größen, d.h. welche
Ergebnisgröße passt zu welcher Kapitalgröße, zu achten:
Wird im Nenner das Eigenkapital gewählt, muss im Zähler der Gewinn nach Zinsen stehen. Diese Rentabilität heißt Eigenkapitalrentabilität.
Wird im Nenner das Gesamtkapital (Eigen- und Fremdkapital)
berücksichtigt, wird im Zähler der Gewinn vor Fremdkapitalzinsen eingesetzt. Diese Rentabilität wird als Gesamtkapitalrentabilität bezeichnet.
Entscheidungsregel: Führe ein Investitionsprojekt durch, wenn seine Kapitalrentabilität größer als die gewünschte Rentabilität ist.
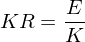
Dabei ist auf die Konsistenz der beiden Größen, d.h. welche
Ergebnisgröße passt zu welcher Kapitalgröße, zu achten:
Wird im Nenner das Eigenkapital gewählt, muss im Zähler der Gewinn nach Zinsen stehen. Diese Rentabilität heißt Eigenkapitalrentabilität.
Wird im Nenner das Gesamtkapital (Eigen- und Fremdkapital)
berücksichtigt, wird im Zähler der Gewinn vor Fremdkapitalzinsen eingesetzt. Diese Rentabilität wird als Gesamtkapitalrentabilität bezeichnet.
Entscheidungsregel: Führe ein Investitionsprojekt durch, wenn seine Kapitalrentabilität größer als die gewünschte Rentabilität ist.
Tags: eigenkapitalrentabilität, gesamtkapitalrentabilität, kapitalrentabilität, rentabilität, rentabilitätsrechnung
Source: IuF Teil 3, Folie 13
Source: IuF Teil 3, Folie 13
Durchschnittliche Kapitalrentabilität


Die durchschnittliche Kapitalrentabilität (DKR) eines bestimmten
Zeithorizonts ist definiert als Quotient aus dem durchschnittlichen Gewinn nach Steuern und Abschreibungen (DG) und dem durchschnittlich gebundenen, zu Buchwerten angesetzten Kapital (DK) innerhalb dieses Zeithorizonts:
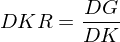
Zeithorizonts ist definiert als Quotient aus dem durchschnittlichen Gewinn nach Steuern und Abschreibungen (DG) und dem durchschnittlich gebundenen, zu Buchwerten angesetzten Kapital (DK) innerhalb dieses Zeithorizonts:
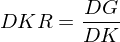
Tags: durchschnittliche kapitalrentabilität
Source: IuF Teil 3, Folie 14
Source: IuF Teil 3, Folie 14
Durchschnittliche Kapitalrentabilität: Diskussion


| Vorteile | |
| Einfache Berechnung | |
| Verfügbarkeit der Inputgrößen uber das Rechnungswesen | |
| Große Beachtung durch Medien und Aktionäre | |
| Gute Eignung zur Vergleichsrechnung verschiedener Investitionsprojekte |
| Nachteile |
| Abhängigkeit von Bilanzierungsregeln und -politik wegen Buchwerten und Ergebnisgröße anstatt Zahlungen |
| Keine Berücksichtigung der zeitlichen Verteilung der Ergebnisgrößen |
| Willkürlichkeit bei der Wahl der geforderten Mindestrentabilität |
Tags: Durchschnittliche Kapitalrentabilität
Source: IuF Teil 3, Folie 17
Source: IuF Teil 3, Folie 17
Interne Zinssatzmethode


| Der interne Zinssatz ist derjenige Zinssatz, bei dem der Kapitalwert einer Investition 0 beträgt |
| Er stellt demnach die Verzinsung des in dem Investitionsprojekt gebundenen Kapitals und damit eine das gesamte Projekt zusammenfassende Kennzahl dar. |
| Entscheidungsregel der internen Zinssatzmethode (IZSM) bei einem normalen Investitionsprojekt: Investiere in ein Investitionsprojekt, wenn dessen interner Zinssatz höher als der geforderte Zinssatz ist. |
Tags: Interne Zinssatzmethode
Source: IuF Teil 3, Folie 18
Source: IuF Teil 3, Folie 18
IZSM: Diskussion


| Vorteile | |
| Eine einzige und einfach zu kommunizierende Kennzahl als Diskussionsgrundlage bei dem Vergleich mehrerer Investitionsprojekte. | |
| Berücksichtigung von mehrperiodischen Zahlungen |
| Nachteile |
| Probleme der internen Zinssatzmethode werden bei der Betrachtung eines einzelnen unabhängigen Projektes sowie zweier sich ausschließender Projekte offensichtlich. |
| Als genereller Nachteil ist die schwierige Berechnung des internen Zinssatzes, besonders bei sehr langen Projekten, zu nennen. |
Tags: interne zinssatzmethode
Source: IuF Teil 3, Folie 21
Source: IuF Teil 3, Folie 21
Tags: interne zinssatzmethode
Source: IuF Teil 3, Folie 21
Source: IuF Teil 3, Folie 21
IZSM: Problem bei einem einzelnen Projekt


Da der Kapitalwert zwischen den beiden internen Zinssätzen positiv ist, kann nach Kapitalwertmethode die Entscheidungsregel lauten:
Investiere, wenn der geforderte Zinssatz für den Kapitalwert zwischen 10% und 20% liegt.
Investiere, wenn der geforderte Zinssatz für den Kapitalwert zwischen 10% und 20% liegt.
Tags: Interne Zinssatzmethode
Source: IuF Teil 3, Folie 23
Source: IuF Teil 3, Folie 23
Tags: Interne Zinssatzmethode
Source: IuF Teil 3, Folie 24
Source: IuF Teil 3, Folie 24
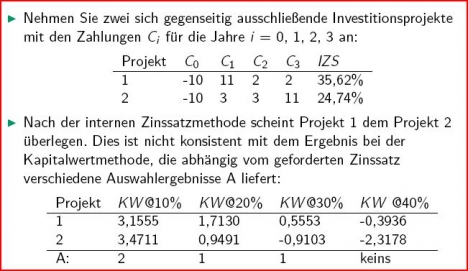
IZSM: Sich gegenseitig ausschließende Projekte
Problem 1/2
Problem 1/2
Hier werden beispielweise die Zahlungen des Projekts 2 von den
Zahlungen des Projekts 1 abgezogen und der daraus resultierende Zahlungsstrom als normales zusätzliches Investitionsprojekt 1-2 gesehen:
Ist dieses Projekt anzunehmen, ist auch das Projekt 1 anzunehmen.
Nach interner Zinssatzmethode bei einem geforderten Zinssatz von 20% ist wegen eines höheren internen Zinssatzes des zusätzlichen Investitionsprojektes 1-2 das Projekt 1 zu wählen. Nach Kapitalwertmethode ergibt sich wegen des positiven Kapitalwerts von Projekt 1-2 dieselbe Entscheidung.
Zahlungen des Projekts 1 abgezogen und der daraus resultierende Zahlungsstrom als normales zusätzliches Investitionsprojekt 1-2 gesehen:
| 1-2 | -7 | 10 | 42,86% | 1,3333 |
Ist dieses Projekt anzunehmen, ist auch das Projekt 1 anzunehmen.
Nach interner Zinssatzmethode bei einem geforderten Zinssatz von 20% ist wegen eines höheren internen Zinssatzes des zusätzlichen Investitionsprojektes 1-2 das Projekt 1 zu wählen. Nach Kapitalwertmethode ergibt sich wegen des positiven Kapitalwerts von Projekt 1-2 dieselbe Entscheidung.
Tags: Interne Zinssatzmethode
Source: IuF Teil 3, Folie 25
Source: IuF Teil 3, Folie 25
Tags: Interne Zinssatzmethode
Source: IuF Teil 3, Folie 26
Source: IuF Teil 3, Folie 26
IZSM: Sich gegenseitig ausschließende Projekte
Problem 2/2

Problem 2/2

| Bei einem Zinssatz von 12,50% herrscht Indifferenz über die Vorteilhaftigkeit eines Projektes über das andere. | |
| Ist der Zinssatz kleiner als 12,50% ist das Projekt 2 vorzuziehen; ist der Zinssatz größer als 12,50% und kleiner als 35,62%, dann ist Projekt 1 zu präferieren. | |
| Die Abhängigkeit von dem gefordeten Zinssatz resultiert aus der zeitlichen Verteilung der Zahlungen beider Projekte. Während Projekt 1 anfänglich hohe und später niedrige Zahlungen generiert, sind die Zahlungen von Projekt 2 am Anfang niedrig und enden hoch. Hohe Zinssätze beispielsweise bedeuten eine hohe Wiederanlage früherer Zahlungen und begünstigen daher Projekt 1. |
Tags: Interne Zinssatzmethode
Source: IuF Teil 3, Folie 28
Source: IuF Teil 3, Folie 28
IZSM: Sich gegenseitig ausschließende Projekte
Problem 2/2
Lösung des Timing-Problems?
=>
Der IZS...
=> Wenn der IZS...
Problem 2/2
Lösung des Timing-Problems?
=>
Der IZS...
=> Wenn der IZS...
=> wie bei Problem 1.
Der IZS dieses Projektes (2-1) entspricht dann dem Zinssatz, bei dem nach der Kapitalwertmethode Indifferenz zwischen den Projekten besteht.
=> Wenn der IZS über dem geforderten Zinssatz liegt, ist das Projekt 2-1 anzunehmen, also auch das Projekt 2! Dies deckt sich auch mit der Kapitalwertmethode, da der Kapitalwert unter 12,50% postitiv ist!

Der IZS dieses Projektes (2-1) entspricht dann dem Zinssatz, bei dem nach der Kapitalwertmethode Indifferenz zwischen den Projekten besteht.
=> Wenn der IZS über dem geforderten Zinssatz liegt, ist das Projekt 2-1 anzunehmen, also auch das Projekt 2! Dies deckt sich auch mit der Kapitalwertmethode, da der Kapitalwert unter 12,50% postitiv ist!

Tags: Interne Zinssatzmethode
Source: IuF Teil 3, Folie 27,29,30
Source: IuF Teil 3, Folie 27,29,30
Arbitrage und die Bewertung von Wertpapieren
Arbitrage

Arbitrage

| Das Ausnutzen unterschiedlicher Preise für äquivalente Güter auf unterschiedlichen Märkten bezeichnet man als Arbitrage. | |
| Konkret bezeichnet man als Arbitragegelegenheit jede Situation, in der es möglich ist, einen sicheren Gewinn ohne eigene Investition zu erzielen. | |
| Wird eine Arbitragegelegenheit entdeckt, werden Marktteilnehmer eine solche ausnutzen und am Markt handeln. Daher werden die Marktpreise sich schnell anpassen und die Arbitragegelegenheit eliminieren. | |
| Einen Finanzmarkt, auf dem keine Arbitragegelegenheiten existieren, bezeichnen wir hier als normalen Markt. |
Tags: arbitrage, arbitragegelegenheit, normaler markt
Source: IuF Teil 4, Folie 3
Source: IuF Teil 4, Folie 3
Bewertung eines Wertpapiers mit sicheren Zahlungen 1/5


Der Betrag entspricht genau dem Barwert von €1000:
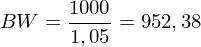
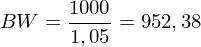
Tags: bewertung, wertpapier
Source: IuF Teil 4, Folie 4
Source: IuF Teil 4, Folie 4
Bewertung eines Wertpapiers mit sicheren Zahlungen 2/5


| Es gibt also demzufolge zwei Wege, die Zahlung von €1.000 in einem Jahr zu erhalten: (1) durch den Kauf des Wertpapiers oder (2) durch die Anlage von €952, 38 zum risikolosen Zinssatz. | |
| Die Behauptung ist nun, dass der Preis für das Wertpapier in einem normalen Markt €952,38 betragen muss. |
Tags: bewertung, wertpapier
Source: IuF Teil 4, Folie 5
Source: IuF Teil 4, Folie 5
Bewertung eines Wertpapiers mit sicheren Zahlungen 3/5
Angenommen, der Preis betrüge €940. Welche Arbitragegelegenheit ergibt sich in diesem Fall?

Angenommen, der Preis betrüge €940. Welche Arbitragegelegenheit ergibt sich in diesem Fall?

Wir können das Wertpapier kaufen und gleichzeitig einen Kredit in Höhe von €952,38 aufnehmen!
Eine solche Strategie ermöglicht eine Zahlung von €12,38, ohne zu
einer zukünftigen Auszahlung zu führen.
| / | Zahlung Heute | Zahlung in einem Jahr |
| Kaufe die Anleihe | -940,00 | +1000,00 |
| Leihe Geld von der Bank | +952,38 | -1000,00 |
| Netto-Zahlung | +12,38 | 0,00 |
Eine solche Strategie ermöglicht eine Zahlung von €12,38, ohne zu
einer zukünftigen Auszahlung zu führen.
Tags: bewertung, wertpapier
Source: IuF Teil 4, Folie 6
Source: IuF Teil 4, Folie 6
Bewertung eines Wertpapiers mit sicheren Zahlungen 4/5


In diesem Fall können wir das Wertpapier (leer)verkaufen und einen Betrag von €952,38 zum risikolosen Zinssatz anlegen.
Dies führt zu einem aktuellen Mittelzufluss von €7,62, dem kein zukünftiger Mittelabfluss gegenübersteht.
Bemerkung: Wenn wir das Wertpapier ursprünglich nicht besitzen, spricht man von einem Leerverkauf.
| / | Zahlung Heute | Zahlung in einem Jahr |
| Verkaufe die Anleihe | +960,00 | -1000,00 |
| Lege Geld bei der Bank an | -952,38 | +1000,00 |
| Netto-Zahlung | +7,62 | 0,00 |
Dies führt zu einem aktuellen Mittelzufluss von €7,62, dem kein zukünftiger Mittelabfluss gegenübersteht.
Bemerkung: Wenn wir das Wertpapier ursprünglich nicht besitzen, spricht man von einem Leerverkauf.
Tags: bewertung, leerverkauf, wertpapier
Source: IuF Teil 4, Folie 7
Source: IuF Teil 4, Folie 7
Bewertung eines Wertpapiers mit sicheren Zahlungen 5/5


| Martktteilnehmer, die Arbitragegelegenheiten entdecken, kaufen bzw. verkaufen das Wertpapier, so dass sich dessen Preis verändert und schnell den Wert von €952, 38 erreicht und die Arbitragegelegenheit verschwindet. | |
| Diesen Preis bezeichnet man auch als “No-Arbitrage-Preis”. | |
| Die Abwesenheit von Arbitragegelegenheiten in normalen Märkten impliziert, dass dort das so genannte Gesetz des einen Preises gilt. | |
| Das Gesetz des einen Preises besagt, dass zahlungsäquivalente Wertpapiere, die in verschiedenen normalen Märkten gehandelt werden, den gleichen Preis besitzen müssen. |
Tags: arbitragegelegenheit, bewertung, gesetz des einen preises, no-arbitrage-preis, normaler markt, wertpapier
Source: IuF Teil 4, Folie 8
Source: IuF Teil 4, Folie 8
Der Kapitalwert von Wertpapieren


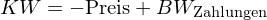
In einem normalen Markt ist der Kapitalwert einer solchen Investition gleich null.
Tags: kapitalwert, wertpapier
Source: IuF Teil 4, Folie 9
Source: IuF Teil 4, Folie 9
Die Bewertung von Portfolios


Das Gesetz des einen Preises impliziert, dass Wertpapier C und das Portfolio aus A und B den gleichen Preis aufweisen müssen:
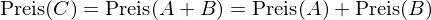
Die Beziehung zwischen des Wertes der einzelnen Wertpapiere eines Portfolios und dem Portfoliowert bezeichnet man als Wertadditivität.
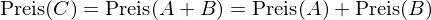
Die Beziehung zwischen des Wertes der einzelnen Wertpapiere eines Portfolios und dem Portfoliowert bezeichnet man als Wertadditivität.
Tags: bewertung, portfolio, wertadditivität
Source: IuF Teil 4, Folie 10
Source: IuF Teil 4, Folie 10
Tags: Risikobehaftete zahlungen, risikolose Zahlungen
Source: IuF Teil 4, Folie 11,12,13
Source: IuF Teil 4, Folie 11,12,13
Risikoaversion


| Intuitiv gesprochen zahlen Investoren weniger für einen risikobehafteten Zahlungsstrom als für einen sicheren, weil sie Risiko scheuen, d.h. der Verlust eines Euro wiegt schwerer als der Gewinn eines Euro. | |
| Im konkreten Fall ist der Vorteil zusätzlicher €300 (1.400 versus 1.100) weniger vorteilhaft als der Nachteil geringerer €300 (800 versus 1.100). | |
| Das Konzept, dass Menschen sichere Zahlungen gegenüber unsicheren mit gleichem Erwartungswert bevorzugen, bezeichnet man als Risikoaversion. | |
| Der Grad der Risikoaversion ist Bestandteil persönlicher Präferenzstrukturen. | |
| Je höher der Grad der Risikoaversion, desto weniger ist ein Investor bereit, für einen risikobehafteten Zahlungsstrom relativ zu einem sicheren gleichen Erwartungswert zu zahlen. |
Tags: risikoaversion
Source: IuF Teil 4, Folie 14
Source: IuF Teil 4, Folie 14
Risikoaversion und Risikoprämie 1/2


Aufgrund der Risikoaversion von Investoren ist es bei der Berechnung des Barwerts risikobehafteter Zahlungsströme unzulässig, den risikolosen Zinssatz zu verwenden.
Auf Basis der erwarteten Zahlungen des Indexinvestment ergibt sich
eine Verzinsung von:
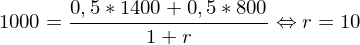
Man spricht bei Verwendung von Zahlungserwartungswerten von
erwarteter Verzinsung oder erwarteter Rendite.
Auf Basis der erwarteten Zahlungen des Indexinvestment ergibt sich
eine Verzinsung von:
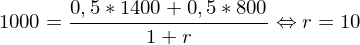
Man spricht bei Verwendung von Zahlungserwartungswerten von
erwarteter Verzinsung oder erwarteter Rendite.
Tags: erwartete rendite, erwartete verzinsung, risikoaversion, risikoprämie
Source: IuF Teil 4, Folie 15
Source: IuF Teil 4, Folie 15
Risikoaversion und Risikoprämie 2/2


Tatsächliche Rendite bei positiver wirtschaftlicher Entwicklung:
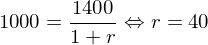
Tatsächliche Rendite bei negativer wirtschaftlicher Entwicklung:
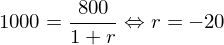
Die erwartete Rendite lässt sich auch als Erwartungswert der tatsächlichen Renditen berechnen: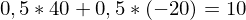
Die Differenz von 6% bezeichnet man als die Risikoprämie der Investition in den Aktienindex.
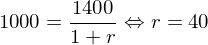
Tatsächliche Rendite bei negativer wirtschaftlicher Entwicklung:
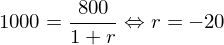
Die erwartete Rendite lässt sich auch als Erwartungswert der tatsächlichen Renditen berechnen:
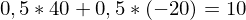
Die Differenz von 6% bezeichnet man als die Risikoprämie der Investition in den Aktienindex.
Tags: erwartete rendite, risikoaversion, risikoprämie
Source: IuF Teil 4, Folie 16
Source: IuF Teil 4, Folie 16
Der No-Arbitrage-Preis eines riskanten Wertpapiers 1/2


| Gegeben die Preise für das risikolose Wertpapier und die Indexinvestition, lassen sich die No-Arbitrage-Preise anderer risikobehafteter Wertpapiere bestimmen. | |
| Eine Kombination des risikolosen Wertpapiers mit Wertpapier A erlaubt es, einen Zahlungsstrom zu generieren, der mit dem der Indexinvestition identisch ist |
Tags: no-arbitrage-preis, riskantes wertpapier
Source: IuF Teil 4, Folie 17
Source: IuF Teil 4, Folie 17
Der No-Arbitrage-Preis eines riskanten Wertpapiers 2/2


| Nach dem Gesetz des einen Preises muss der gemeinsame Marktwert der Position des risikolosen Wertpapiers und des Wertpapiers A mit dem Preis der Indexinvestition übereinstimmen. | |
| Die Position des risikolosen Wertpapiers bei einem risikolosen Zinssatz von 4% hat einen No-Arbitrage-Preis von €769. | |
| Demzufolge beträgt der No-Arbitrage-Preis von Wertpapier A : 1000-769 = 231 | |
| Dies impliziert eine erwartete Rendite von 30% und eine Risikoprämie von 26%. |
Tags: No-Arbitrage-Preis, riskantes Wertpapier
Source: IuF Teil 4, Folie 18
Source: IuF Teil 4, Folie 18
Bewertung von Wertpapieren (Zusammenfassung)


| Wenn die Zahlungen des betrachteten Wertpapiers durch existierende Wertpapiere vollständig nachgebildet werden können, so ist dessen Wert durch das Gesetz des einen Preises bestimmt. | |
| Wenn die Zahlungen des Wertpapiers nicht durch existierende Wertpapiere nachgebildet werden können, bestimme die erwarteten Zahlungen an jedem Zeitpunkt und diskontiere diese mit dem Zinssatz, der die Risikoprämie korrekt abbildet. |
Tags: bewertung, risikoprämie, wertpapier. erwartete zahlungen
Source: IuF Teil 4, Folie 19
Source: IuF Teil 4, Folie 19
Bewertung risikoloser Anleihen: Zerobonds 1/2


Als risikolose Anleihen werden diejenigen bezeichnet, deren
Zahlungsstrom sicher ist.
Die Anleihen mit der einfachsten Zahlungsstruktur sind Zerobonds
(Nullkuponanleihen), deren einzige Zahlung die Rückzahlung des
Nennwerts bei Fälligkeit der Anleihe ist.
Die Beziehung zwischen Preis und internem Zinssatz eines Zerobond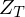 mit Fälligkeit zum Zeitpunkt
mit Fälligkeit zum Zeitpunkt 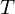 lässt sich ausdrücken als:
lässt sich ausdrücken als:
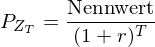
Zahlungsstrom sicher ist.
Die Anleihen mit der einfachsten Zahlungsstruktur sind Zerobonds
(Nullkuponanleihen), deren einzige Zahlung die Rückzahlung des
Nennwerts bei Fälligkeit der Anleihe ist.
Die Beziehung zwischen Preis und internem Zinssatz eines Zerobond
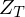 mit Fälligkeit zum Zeitpunkt
mit Fälligkeit zum Zeitpunkt 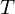 lässt sich ausdrücken als:
lässt sich ausdrücken als: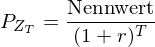
Tags: bewertung, risikolose anleihe, zerobond
Source: IuF Teil 4, Folie 20
Source: IuF Teil 4, Folie 20
Bewertung risikoloser Anleihen: Kuponanleihen 1/2


Bei Kuponbonds fallen außer der Rückzahlung des Nennwertes
zwischenzeitliche Zinszahlungen an (die Kupons).
Mit Hilfe des aus Zerobonds ermittelten risikolosen Zinssatzes lässt
sich ein risikoloser Kuponbond nach dem Gesetz des einen Preises bestimmen.
Beispiel: a) Bestimmen Sie den arbitragefreien Preis,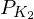 , einer zweijährigen Anleihe mit Nennwert 100 und einem jährlichen Kupon von 10% bei einem risikolosen Zinssatz von 5%.
, einer zweijährigen Anleihe mit Nennwert 100 und einem jährlichen Kupon von 10% bei einem risikolosen Zinssatz von 5%.
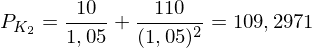
zwischenzeitliche Zinszahlungen an (die Kupons).
Mit Hilfe des aus Zerobonds ermittelten risikolosen Zinssatzes lässt
sich ein risikoloser Kuponbond nach dem Gesetz des einen Preises bestimmen.
Beispiel: a) Bestimmen Sie den arbitragefreien Preis,
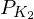 , einer zweijährigen Anleihe mit Nennwert 100 und einem jährlichen Kupon von 10% bei einem risikolosen Zinssatz von 5%.
, einer zweijährigen Anleihe mit Nennwert 100 und einem jährlichen Kupon von 10% bei einem risikolosen Zinssatz von 5%.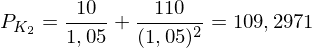
Tags: bewertung, kuponanleihe, risikolose anleihe, zerobond
Source: IuF Teil 4, Folie 23
Source: IuF Teil 4, Folie 23
Bewertung risikoloser Anleihen: Kuponanleihen 2/2
1. Nehmen sie an, der beobachtete Preis betrage 110. Zeigen Sie eine Strategie auf, die zu einem Arbitragegewinn führt
(Es existieren ein einjähriger und ein zweijähriger Zerobond, die jeweils einen Yield von 5% und einen Nennwert von 100 besitzen.)
2. Während Zerobonds unterhalb ihres Nennwerts notieren, ...
1. Nehmen sie an, der beobachtete Preis betrage 110. Zeigen Sie eine Strategie auf, die zu einem Arbitragegewinn führt
(Es existieren ein einjähriger und ein zweijähriger Zerobond, die jeweils einen Yield von 5% und einen Nennwert von 100 besitzen.)
2. Während Zerobonds unterhalb ihres Nennwerts notieren, ...

Tags: bewertung, kuponanleihe, kuponbond, riskolose anleihe, zerobond
Source: IuF Teil 4, Folie 24
Source: IuF Teil 4, Folie 24
Dynamischer Verlauf von Anleihepreisen


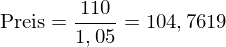
Bei Betrachtung von Zeitpunkten kurz nach einer Kuponzahlung gilt
folgendes:
Bei konstantem risikolosem Zinssatz fallen im Zeitablauf diejenigen Anleihen im Wert, deren arbitragefreie Preise über dem Nennwert liegen.
Umgekehrt steigen bei konstantem risikolosem Zinssatz im Zeitablauf diejenigen Anleihen im Wert, deren arbitragefreie Preise unter dem Nennwert liegen.
Tags: dynamischer verlauf von anleihepreisen, kuponzahlung
Source: IuF Teil 4, Folie 25
Source: IuF Teil 4, Folie 25
Bewertung von Aktien


| Der von einer Aktie generierte Zahlungsstrom ist unsicher. | |
| Eine Duplikation des Zahlungsstroms mit anderen Wertpapieren (außer den eigenen sogenannten Derivaten) ist unwahrscheinlich. | |
| Daher wenden wir für die Aktienbewertung die Methode der Diskontierung der bei einem Aktieninvestment erwarteten Zahlungen an. | |
| An dieser Stelle konzentrieren wir uns auf die Bestimmung der erwarteten Zahlungen |
Tags: aktien, bewertung
Source: IuF Teil 4, Folie 27
Source: IuF Teil 4, Folie 27
Aktienbewertung: Investorin mit Einjahreshorizont


| Zum einen entstehen Zahlungen, wenn das Unternehmen während der Haltedauer Dividenden ausschüttet. Zum anderen entsteht ein Mittelzufluss, wenn die Investorin sich entscheidet, die Aktien zu veräußern. | |
| Betrachten wir hier eine Investorin mit einem Anlagehorizont von einem Jahr. Wenn es zu einer Dividendenzahlung während des Jahres kommt, dann erfolgt diese am Ende des Anlagezeitraums. | |
Die Zahlungen aus dem Investment sind die Auszahlung beim Erwerb in Zeitpunkt 0, 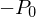 , sowie die Einzahlungen nach einem Jahr in Form des Veräußerungspreises, , sowie die Einzahlungen nach einem Jahr in Form des Veräußerungspreises, 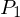 , plus evtl. einer Dividende, , plus evtl. einer Dividende, 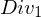 . . |
Tags: aktien, bewertung
Source: IuF Teil 4, Folie 28
Source: IuF Teil 4, Folie 28
Aktienbewertung: Dividend Discount Model 1/2


Als Bewertungsgleichung ergibt sich, wenn der adäquate, das Risiko
berücksichtigende Diskontierungssatz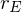 beträgt:
beträgt:
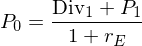
Die Investorin muss also sowohl die erwartete Dividende als auch den erwarteten Veräußerungspreis bestimmen.
Der Veräußerungspreis bestimmt sich aus dem Kalkül eines anderen Investors, dessen Bewertungsgleichung lautet:
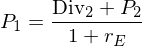
Damit wird die Gleichung der ursprünglichen Investorin zu:
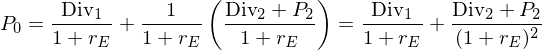
berücksichtigende Diskontierungssatz
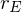 beträgt:
beträgt: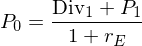
Die Investorin muss also sowohl die erwartete Dividende als auch den erwarteten Veräußerungspreis bestimmen.
Der Veräußerungspreis bestimmt sich aus dem Kalkül eines anderen Investors, dessen Bewertungsgleichung lautet:
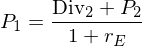
Damit wird die Gleichung der ursprünglichen Investorin zu:
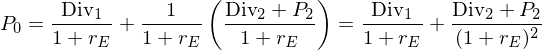
Tags: aktie, bewertung, Dividend Discount Model
Source: IuF Teil 4, Folie 29
Source: IuF Teil 4, Folie 29
Aktienbewertung: Dividend Discount Model 2/2


Durch weitere Anwendung dieser Logik ergibt sich der Wert einer
Aktie als:
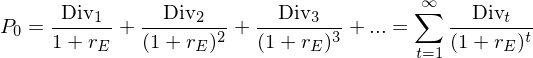
Dies bedeutet, dass der Preis einer Aktie sich ergibt als Barwert aller erwarteten Dividendenzahlungen.
Insbesondere impliziert dieses Resultat, dass der Anlagehorizont für den Wert einer Aktie unerheblich ist. Da bei Veräußerung immer ein Käufer gefunden werden muss, sind in jedem Fall die gesamten zukünftigen Zahlungen einer Aktie für deren Bewertung relevant.
Aktie als:
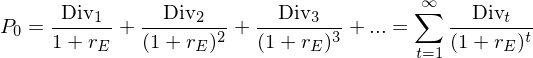
Dies bedeutet, dass der Preis einer Aktie sich ergibt als Barwert aller erwarteten Dividendenzahlungen.
Insbesondere impliziert dieses Resultat, dass der Anlagehorizont für den Wert einer Aktie unerheblich ist. Da bei Veräußerung immer ein Käufer gefunden werden muss, sind in jedem Fall die gesamten zukünftigen Zahlungen einer Aktie für deren Bewertung relevant.
Tags: aktie, bewertung, dividend discount model
Source: IuF Teil 4, Folie 30
Source: IuF Teil 4, Folie 30
Ertrag und Risiko im Gleichgewicht
Gleichgewichtstheorie (CAPM)

Gleichgewichtstheorie (CAPM)

Portefeuille-Theorie als Fundament der modernen Kapitalmarkttheorie
Abwägen zwischen Ertrag und Risiko
Ökonomische Idee: Durch Erwerb verschiedener Aktien kann Risikominderung (Diversifikation) erreicht werden.
Was passiert, wenn alle Investoren gemäß obiger Theorie agieren?
liefert, D.h. zentrales Ergebnis der Theorie
„fairer“ Preis für übernommenes Risiko
Abwägen zwischen Ertrag und Risiko
Ökonomische Idee: Durch Erwerb verschiedener Aktien kann Risikominderung (Diversifikation) erreicht werden.
Was passiert, wenn alle Investoren gemäß obiger Theorie agieren?
| Gleichgewichtstheorie (CAPM), die Zusammenhang zwischen |
| Risiko und |
| angemessener erwarteter Rendite |
liefert, D.h. zentrales Ergebnis der Theorie
„fairer“ Preis für übernommenes Risiko
Tags: capm, ertrag, erwartete rendite, gleichgewichtstheorie, risiko
Source: IuF Teil 5, Folie 3
Source: IuF Teil 5, Folie 3
Renditen


Rendite (in €): Dividendenzahlung zuzüglich der Veränderung des Vermögenswertes ausgedrückt in Geldeinheiten
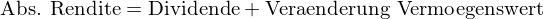
Prozentuale Rendite: Dividendenzahlung zuzüglich der Veränderung des Vermögenswertes bezogen auf den anfänglichen Vermögenswert (= Investitionssumme)
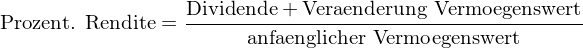
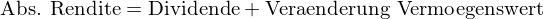
Prozentuale Rendite: Dividendenzahlung zuzüglich der Veränderung des Vermögenswertes bezogen auf den anfänglichen Vermögenswert (= Investitionssumme)
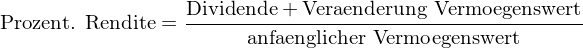
Tags: renditen
Source: IuF Teil 5, Folie 4
Source: IuF Teil 5, Folie 4
Halteperiode Rendite
Halteperiode Rendite: Rendite die der Investor erhält, wenn er eine Investition über eine Periode von  Jahren hält, wobei die Rendite für jedes Jahr
Jahren hält, wobei die Rendite für jedes Jahr  mit
mit 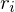 gegeben ist!
gegeben ist!
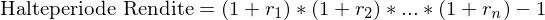
Geometrisch durchschnittliche Rendite (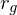 ):
):
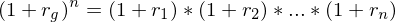
Arithmetisch durchschnittliche Rendite (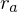 ):
):
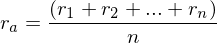
 Jahren hält, wobei die Rendite für jedes Jahr
Jahren hält, wobei die Rendite für jedes Jahr  mit
mit 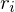 gegeben ist!
gegeben ist!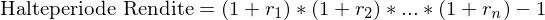
Geometrisch durchschnittliche Rendite (
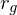 ):
):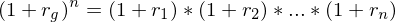
Arithmetisch durchschnittliche Rendite (
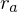 ):
):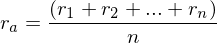
Tags: halteperiode rendite
Source: IuF Teil 5, Folie 5
Source: IuF Teil 5, Folie 5
Rendite- und Risiko-Statistiken


Durchschnittliche Rendite:
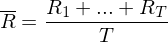
Standardabweichung der Renditen:
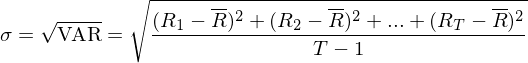
(eigentlich ist das ja s* und nicht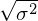 )
)
In der Literatur werden für die Risikomaße häufig die Varianz und Standardabweichung der Renditen herangezogen.
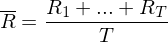
Standardabweichung der Renditen:
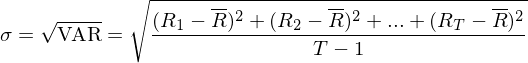
(eigentlich ist das ja s* und nicht
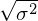 )
)In der Literatur werden für die Risikomaße häufig die Varianz und Standardabweichung der Renditen herangezogen.
Tags: rendite, risiko, statisiken
Source: IuF Teil 5, Folie 7
Source: IuF Teil 5, Folie 7
Einzelne Wertpapiere: Erwartete Rendite und Risiko

Gesucht: erwartete Renditen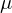 und Risiko (Standardabweichung
und Risiko (Standardabweichung  ) der Renditen
) der Renditen

Gesucht: erwartete Renditen
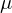 und Risiko (Standardabweichung
und Risiko (Standardabweichung  ) der Renditen
) der Renditen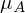 = 1/3 * (-7%) + 1/3 * 12% + 1/3 * 28% = 11%
= 1/3 * (-7%) + 1/3 * 12% + 1/3 * 28% = 11%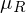 = 1/3 * 17% + 1/3 * 7% + 1/3 * (-3%) = 7%
= 1/3 * 17% + 1/3 * 7% + 1/3 * (-3%) = 7%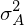 = 1/3 * (−7%−11%)² + 1/3 * (12%−11%)² + 1/3 * (28%−11%)² = 0,0205
= 1/3 * (−7%−11%)² + 1/3 * (12%−11%)² + 1/3 * (28%−11%)² = 0,0205 =>
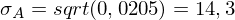
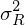 = 1/3 * (17%-7%)² + 1/3 * (7%-7%)² + 1/3 * (-3%-7%)² = 0,0067
= 1/3 * (17%-7%)² + 1/3 * (7%-7%)² + 1/3 * (-3%-7%)² = 0,0067 =>
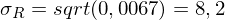
| Szenario | W'keit | Aktienfonds | Rentenfonds |
| Rezession | 1/3 | -7% | 17% |
| Normal | 1/3 | 12% | 7% |
| Boom | 1/3 | 28% | -3% |
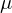 | - | 11% | 7% |
 | - | 14,3% | 8,2% |
Tags: einzelne wertpapiere, erwartete rendite, risiko
Source: IuF Teil 5, Folie 10,11,12
Source: IuF Teil 5, Folie 10,11,12
Portfeuilles


Investoren betrachten nicht das isolierte Ergebnis einzelner
Wertpapiere sondern das Ergebnis ihres Portefeuilles.
Im Folgenden Portefeuilles aus zwei Wertpapieren:
Portfeuillerendite: gewichtete Summe der Einzelrenditen
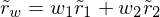
mit Portfeuilleanteilen
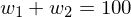
Wertpapiere sondern das Ergebnis ihres Portefeuilles.
Im Folgenden Portefeuilles aus zwei Wertpapieren:
Portfeuillerendite: gewichtete Summe der Einzelrenditen
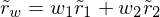
mit Portfeuilleanteilen
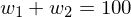
Tags: portfeuilleanteil, portfeuillerendite, portfeuilles, portfolio
Source: IuF Teil 5, Folie 13
Source: IuF Teil 5, Folie 13
Portefeuilles: Portefeuilleanteile
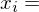
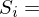

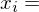
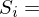

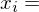 Stückzahl der Aktie
Stückzahl der Aktie 
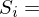 Aktienkurs der Aktie
Aktienkurs der Aktie 
Wert des Portfeuilles:
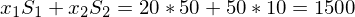
Portefeuilleanteile:
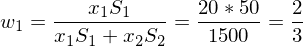
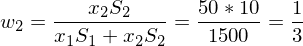
Tags: Portefeuilleanteile, Portefeuilles
Source: IuF Teil 5, Folie 14
Source: IuF Teil 5, Folie 14
Portefeuilles: Erwartungswert der Portefeuillerendite


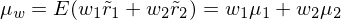
| Erwartete Portefeuillerendite entspricht der gewichteten Summe der erwarteten Renditen der im Portefeuille enthaltenen Wertpapieren. | |
| Gewichtung erfolgt mit Portefeuilleanteilen |
Tags: Erwartungswert, Portefeuillerendite, Portefeuilles
Source: IuF Teil 5, Folie 15
Source: IuF Teil 5, Folie 15
Portefeuilles: Risiko der Portefeuillerendite


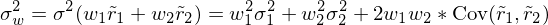
Achtung: Varianz der Portefeuillerendite ergibt sich nicht einfach als gewichtete Summe der einzelnen Varianzen. Kovarianz spielt wichtige Rolle.
Kovarianz der Renditen:
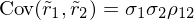
mit der Korrelation
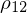 der Einzelrenditen
der EinzelrenditenZur Erinnerung
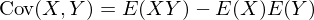
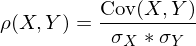
Tags: Portefeuillerendite, Portefeuilles, Risiko
Source: IuF Teil 5, Folie 16
Source: IuF Teil 5, Folie 16
Portefeuilles: Beispiel
Beispiel 1 (Fortsetzung): Betrachte nun Portefeuille, das zu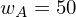 aus Aktien und zu
aus Aktien und zu 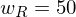 aus Anleihen besteht
aus Anleihen besteht

Beispiel 1 (Fortsetzung): Betrachte nun Portefeuille, das zu
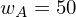 aus Aktien und zu
aus Aktien und zu 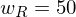 aus Anleihen besteht
aus Anleihen besteht
Portefeuillerendite:
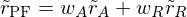
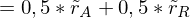
Rezession: 5%, Normal: 9,5%, Boom: 12,5%
erwartete Portefeuillerendite:
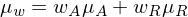
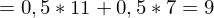
Varianz der Portefeuillerendite:
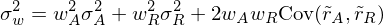
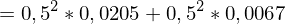
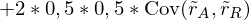
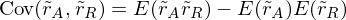
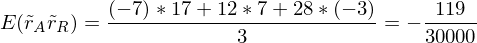
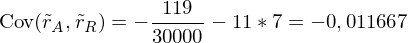
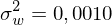
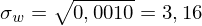
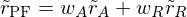
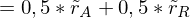
Rezession: 5%, Normal: 9,5%, Boom: 12,5%
erwartete Portefeuillerendite:
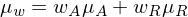
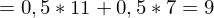
Varianz der Portefeuillerendite:
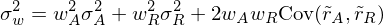
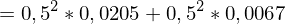
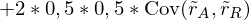
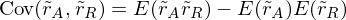
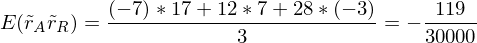
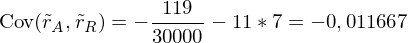
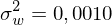
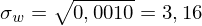
Tags: portefeuilles
Source: IuF Teil 5, Folie 17,18,19,20
Source: IuF Teil 5, Folie 17,18,19,20
Tags: Kombinationen, Portefeuilles, Rendite, Risiko
Source: IuF Teil 5, Folie 21
Source: IuF Teil 5, Folie 21
Portefeuilles: erreichbare Rendite/Risiko-Kombinationen


| Einfluss des Korrelationskoeffizienten auf Ausmaß der Diversifikationsmöglichkeiten | |
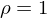 : Keine Risikoreduktion möglich : Keine Risikoreduktion möglich | |
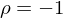 : Risiko kann vollständig eliminiert werden : Risiko kann vollständig eliminiert werden |
Grafik:
oben links:
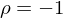
mitte rechts:
Kurve:
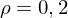
Tags: Kombinationen, Portefeuilles, Rendite, Risiko
Source: IuF Teil 5, Folie 22
Source: IuF Teil 5, Folie 22
Portefeuilles: erreichbare Rendite/Risiko-Kombinationen
* Linie charakterisiert.....
* Portefeuille mit kleinster Varianz: ...
Welches Portefeuille soll Investor wählen?

* Linie charakterisiert.....
* Portefeuille mit kleinster Varianz: ...
Welches Portefeuille soll Investor wählen?

| Linie charakterisiert erreichbare Portefeuilles | |
| Portefeuille mit kleinster Varianz: Minimum Varianz Portefeuille | |
| % | |
| Portefeuilles oberhalb des MVP sind effizient (Effizienter Rand). | |
| Investor wählt effizientes Portefeuille | |
| Konkrete Wahl hängt von Risikoneigung ab |
Tags: Kombinationen, Portefeuilles, Rendite, Risiko
Source: IuF Teil 5, Folie 23,24
Source: IuF Teil 5, Folie 23,24
Portefeuilles: erreichbare Rendite/Risiko-Kombinationen mit
risikolosem Wertpapier

risikolosem Wertpapier

| Portefeuillerendite: | 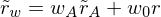 |
| Erwartete Rendite: | 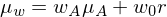 |
| Risiko: | 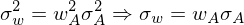 |
Tags: Kombinationen, Portefeuilles, Rendite, Risiko, risikoloses Wertpapier
Source: IuF Teil 5, Folie 25
Source: IuF Teil 5, Folie 25
Portefeuilles: erreichbare Rendite/Risiko-Kombinationen mit
risikolosem Wertpapier
Investor hält Kombination aus
*
*
Effiziente Portefeuilles....
risikolosem Wertpapier
Investor hält Kombination aus
*
*
Effiziente Portefeuilles....

Tags: Kombinationen, Portefeuilles, Rendite, Risiko, risikoloses Wertpapier
Source: IuF Teil 5, Folie 26
Source: IuF Teil 5, Folie 26
Portefeuilles: erreichbare Rendite/Risiko-Kombinationen mit
risikolosem Wertpapier

risikolosem Wertpapier

| Portefeuille A | Investor (sehr risikoavers) investiert Teil seines Vermögens in risikoloses Instrument und Teil in Tangentialportefeuille |
| Portefeuille B | Investor (weniger risikoavers) verschuldet sich risikolos und investiert alles in Tangentialportefeuille |
Tags:
Source: IuF Teil 5, Folie 27
Source: IuF Teil 5, Folie 27
Capital Asset Pricing Model (CAPM): Annahme des CAPM


| a) Investoren | |
sind einperiodige 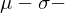 Optimierer (gemäß Portefeuilletheorie) Optimierer (gemäß Portefeuilletheorie) | |
besitzen die gleichen Erwartungen 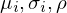 _ij _ij | |
| b) Kapitalmärkte | |
| sind friktionslos | |
| bestehen aus N verschiedenen Aktien mit festem Angebot und | |
| einem risikolosen Instrument |
Tags: CAPM
Source: IuF Teil 5, Folie 29
Source: IuF Teil 5, Folie 29
Vom Individualkalkül zum Gleichgewicht


| Zusammensetzung des Tangentialportefeuilles für alle Investoren identisch |
| Aufteilung zwischen Tangentialportefeuille u. risikolosem Instrument investorspezifisch |
Bsp:
| Investment i | Investor 1: Portefeuilleanteil | Investor 2: Portefeuilleanteil |
| risikolos | 50% | 0% |
| riskant | ||
| Aktie A | 30% | 60% |
| Aktie B | 20% | 40% |
Tags: Gleichgewicht, Individualkalkül
Source: IuF Teil 5, Folie 32
Source: IuF Teil 5, Folie 32
Vom Individualkalkül zum Gleichgewicht
Aus Individualkalkül ergibt sich Nachfrage der beiden Investoren in € (in Stück)
Bsp. Anfangsvermögen der Investoren je 1.000 €
Aktienkurse in t = 0: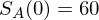 €,
€, 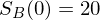 €
€
Aus Individualkalkül ergibt sich Nachfrage der beiden Investoren in € (in Stück)
Bsp. Anfangsvermögen der Investoren je 1.000 €
Aktienkurse in t = 0:
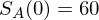 €,
€, 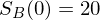 €
€
Tags: Gleichgewicht, Individualkalkül
Source: IuF Teil 5, Folie 37
Source: IuF Teil 5, Folie 37
Vom Individualkalkül zum Gleichgewicht

Was passiert nun?

Was passiert nun?
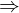 Anpassung der Kurse heute derart, dass Markträumung stattfindet.
Anpassung der Kurse heute derart, dass Markträumung stattfindet.d.h.
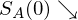 und
und 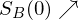 bis jeweils Gesamtnachfrage = Angebot
bis jeweils Gesamtnachfrage = AngebotErgebnis nach Anpassung: Jeder Investor legt sein riskantes Vermögen in der gleichen Zusammensetzung wie das Marktportefeuille an.
Tags: Gleichgewicht, Individualkalkül
Source: IuF Teil 5, Folie 38
Source: IuF Teil 5, Folie 38
Effiziente Portefeuilles im Gleichgewicht


| erwartete Rendite | risikolose Rendite | Preis pro Einheit Risiko | Risikomenge |
Alle effizienten Portefeuilles liegen auf einer Geraden, der Kapitalmarktlinie
Tags: effiziente portefeuilles, gleichgewicht, kapitalmarktlinie
Source: IuF Teil 5, Folie 39
Source: IuF Teil 5, Folie 39
Die Kapitalmarktlinie: effiziente Portefeuilles im
Gleichgewicht

Gleichgewicht

| Jeder Investor legt sein riskantes Vermögen in der gleichen Zusammensetzung wie das Marktportefeuille an. |
| Die risikolose Komponente wird durch den Grad der individuellen Risikoaversion bestimmt |
| Der Marktpreis des Risikos gibt an, wieviel zusätzliche Rendite im Gleichgewicht für eine Einheit zusätzlichen Risikos zu erwarten ist |
| Einziges effizientes (reines) Aktienportefeuille ist das Marktportefeuille. |
Tags: effiziente Portefeuilles, Gleichgewicht, Kapitalmarktlinie
Source: IuF Teil 5, Folie 40
Source: IuF Teil 5, Folie 40
Was ist mit einzelnen Aktien und ineffizienten Portefeuilles?


Ökonomische Idee:
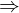 nur Risiko des Marktportefeuilles wichtig!
nur Risiko des Marktportefeuilles wichtig!
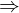 auch für einzelnes Wertpapier
auch für einzelnes Wertpapier 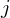 ist nur Beitrag zum Risiko des Marktportefeuilles
ist nur Beitrag zum Risiko des Marktportefeuilles 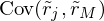 relevant
relevant
Lineare Rendite/Risiko-Beziehung bleibt erhalten, aber Risiko wird nun anders gemessen!
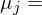
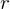
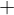
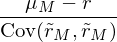
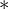
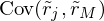
mit Beta-Faktor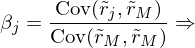
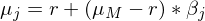
 nur Risiko des Marktportefeuilles wichtig!
nur Risiko des Marktportefeuilles wichtig! auch für einzelnes Wertpapier
auch für einzelnes Wertpapier 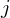 ist nur Beitrag zum Risiko des Marktportefeuilles
ist nur Beitrag zum Risiko des Marktportefeuilles 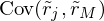 relevant
relevantLineare Rendite/Risiko-Beziehung bleibt erhalten, aber Risiko wird nun anders gemessen!
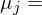
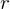
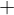
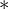
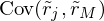
mit Beta-Faktor
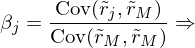
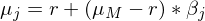
Tags: einzelne Wertpapiere, Gleichgewicht, Wertpapiermarktlinie
Source: IuF Teil 5, Folie 41
Source: IuF Teil 5, Folie 41
Flashcard set info:
Author: sundance
Main topic: BWL
Topic: Unternehmensführung
School / Univ.: KIT
City: Karlsruhe
Published: 12.04.2010
Card tags:
All cards (103)
abzinsen (1)
aktie (4)
aktien (4)
arbitrage (1)
aufzinsen (1)
Barwert (4)
barwert (1)
bewertung (15)
CAPM (1)
capm (1)
commercial paper (1)
covenants (1)
eigenkapital (1)
Endliche Rente (1)
endwert (2)
Endwert (3)
ertrag (1)
Erwartungswert (1)
Ewige Rente (1)
fazit (1)
finanzierung (2)
finanzwirtschaft (1)
fremdkapital (1)
Gleichgewicht (6)
gleichgewicht (1)
Individualkalkül (3)
industrieanleihe (1)
investition (3)
kapitalwert (4)
kapitalwertrate (5)
kernprinzipien (3)
Kombinationen (5)
kreditarten (2)
kreditlinie (1)
kuponanleihe (2)
kuponbond (1)
kuponzahlung (1)
leerverkauf (1)
methodologie (1)
normaler markt (2)
portefeuilles (1)
Portefeuilles (8)
portfeuilles (1)
portfolio (2)
Rendite (5)
rendite (1)
renditen (1)
rentabilität (1)
Rentenformeln (4)
rentenformeln (1)
risiko (3)
Risiko (7)
risikoaversion (3)
risikoprämie (3)
stammaktien (1)
statisiken (1)
tilgungsformen (1)
vermögenswerte (1)
vorzugsaktien (1)
wandelanleihe (1)
wertadditivität (1)
wertpapier (6)
wertschöfpung (1)
zerobond (3)
zinsformen (1)




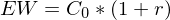

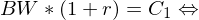
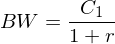
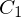 | Zahlung in Jahr 1
| Zahlung in Jahr 1
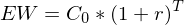

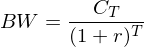
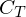 | Zahlung zum Zeitpunkt
| Zahlung zum Zeitpunkt 

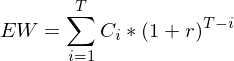

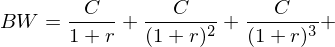 ...
... 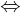
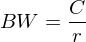

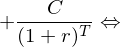
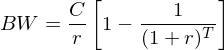

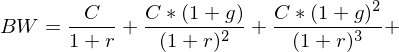 ...
... 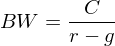

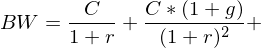 ...
...