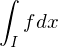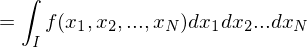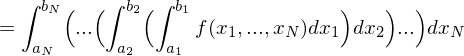Def.: Metrik
Sei 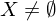 .
.
Eine Abbildung heißt Metrik oder Abstand, falls für alle
heißt Metrik oder Abstand, falls für alle  gilt:
gilt:
1.
positive Definitheit
2.
Symmetrie
3.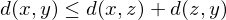
Dreiecksungleichung
 heißt dann metrischer Raum.
heißt dann metrischer Raum.
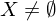 .
.Eine Abbildung
 heißt Metrik oder Abstand, falls für alle
heißt Metrik oder Abstand, falls für alle  gilt:
gilt:1.

positive Definitheit
2.

Symmetrie
3.
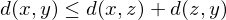
Dreiecksungleichung
 heißt dann metrischer Raum.
heißt dann metrischer Raum.Def.: konvergente Folge im metrischen Raum
Eine Folge 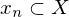 heißt konvergent gegen
heißt konvergent gegen 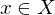
 , wenn für alle
, wenn für alle  ein
ein 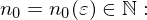
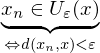
für alle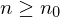
Folgerung
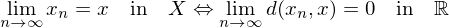
Bemerkung
Konvergenz im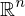 ist äquivalent zur koordinatenweise Konvergenz.
ist äquivalent zur koordinatenweise Konvergenz.
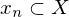 heißt konvergent gegen
heißt konvergent gegen 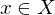
 , wenn für alle
, wenn für alle  ein
ein 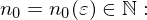
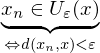
für alle
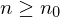
Folgerung
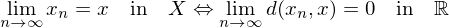
Bemerkung
Konvergenz im
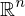 ist äquivalent zur koordinatenweise Konvergenz.
ist äquivalent zur koordinatenweise Konvergenz.Def.: Punkte von M
Sei  ein metrischer Raum,
ein metrischer Raum, 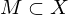 .
.
Ein Punkt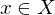 heißt:
heißt:
innerer Punkt von , wenn
, wenn 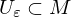 für ein
für ein 
äußerer Punkt von , wenn
, wenn 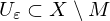 für ein
für ein 
Randpunkt von , wenn
, wenn  und
und
 für alle
für alle 
Häufungspunkt von , wenn
, wenn 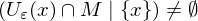 für alle
für alle 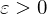
isolierter Punkt von , wenn
, wenn 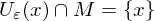 für ein
für ein  .
.  ist kein Häufungspunkt.
ist kein Häufungspunkt.
(z.B. für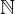 ist jedes
ist jedes  ein isolierter
ein isolierter
Punkt von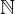 )
)
 ein metrischer Raum,
ein metrischer Raum, 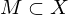 .
. Ein Punkt
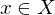 heißt:
heißt:innerer Punkt von
 , wenn
, wenn 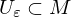 für ein
für ein 
äußerer Punkt von
 , wenn
, wenn 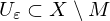 für ein
für ein 
Randpunkt von
 , wenn
, wenn  und
und  für alle
für alle 
Häufungspunkt von
 , wenn
, wenn 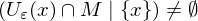 für alle
für alle 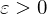
isolierter Punkt von
 , wenn
, wenn 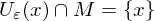 für ein
für ein  .
.  ist kein Häufungspunkt.
ist kein Häufungspunkt. (z.B. für
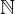 ist jedes
ist jedes  ein isolierter
ein isolierter Punkt von
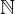 )
)Def.: Mengen von M
Das Innere  ist die Menge aller inneren Punkte von M.
ist die Menge aller inneren Punkte von M.
Das Äußere ist die Menge aller äußeren Punkte von M.
ist die Menge aller äußeren Punkte von M.
Der Rand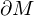 ist die Menge aller Randpunkte von M.
ist die Menge aller Randpunkte von M.
 ist Häufungspunkt von M:
ist Häufungspunkt von M:

 heißt Abschluss oder abgschlossene Hülle von
heißt Abschluss oder abgschlossene Hülle von  .
.
Beispiel
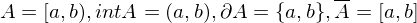
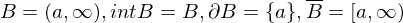
 ist die Menge aller inneren Punkte von M.
ist die Menge aller inneren Punkte von M.Das Äußere
 ist die Menge aller äußeren Punkte von M.
ist die Menge aller äußeren Punkte von M.Der Rand
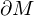 ist die Menge aller Randpunkte von M.
ist die Menge aller Randpunkte von M. ist Häufungspunkt von M:
ist Häufungspunkt von M:
 heißt Abschluss oder abgschlossene Hülle von
heißt Abschluss oder abgschlossene Hülle von  .
.Beispiel
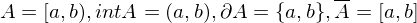
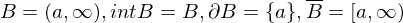
Def.: offen, abgeschlossen, ...
Die Menge  heißt:
heißt:
offen wenn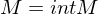
abgeschlossen wenn
dicht in , wenn
, wenn 
beschränkt, wenn
Beispiel
Für eine dichte Menge:
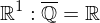 , d.h.
, d.h.  liegt dicht in
liegt dicht in 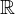
 heißt:
heißt:offen wenn
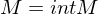
abgeschlossen wenn

dicht in
 , wenn
, wenn 
beschränkt, wenn

Beispiel
Für eine dichte Menge:
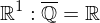 , d.h.
, d.h.  liegt dicht in
liegt dicht in 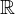
Eigeschaften offener Mengen
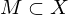 ist offen
ist offen 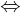 Mit jedem
Mit jedem 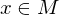 liegt auch
liegt auch 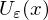 in
in  für ein
für ein  .
.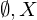 sind offene Mengen.
sind offene Mengen.Die Vereinigung beliebig vieler offener Mengen ist wieder offen.
Der Durchschnitt endlich vieler offener Mengen ist wieder offen.
(Der Durchschnitt unendlich vieler Mengen ist aber nicht offen)
Eigenschaften abgeschlossener Mengen
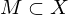 ist abgeschlossen
ist abgeschlossen 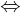 Jeder Häufungspunkt von
Jeder Häufungspunkt von  gehört zu
gehört zu  .
. ist abgschlossen genau dann, wenn
ist abgschlossen genau dann, wenn 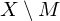 offen ist.
offen ist.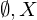 sind abgeschlossen
sind abgeschlossenDer Durchschnitt beliebig vieler abgeschlossener Mengen ist wieder abgeschlossen. Die Vereinigung endlich vieler abgeschlossener Mengen ist wieder abgeschlossen.
Def.: Cauchy-Folge
Sei 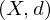 ein metrischer Raum. Dann heißt
ein metrischer Raum. Dann heißt 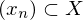 Cauchy-Folge oder Fundamentalfolge, falls für jedes
Cauchy-Folge oder Fundamentalfolge, falls für jedes  ein
ein 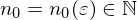 existiert mit
existiert mit 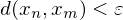 für alle
für alle 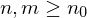 .
.
Folgerung
1. Jede konvergente Folge aus ist eine Cauchy-Folge.
ist eine Cauchy-Folge.
2. Jede Cachy-Folge ist beschränkt.
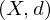 ein metrischer Raum. Dann heißt
ein metrischer Raum. Dann heißt 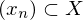 Cauchy-Folge oder Fundamentalfolge, falls für jedes
Cauchy-Folge oder Fundamentalfolge, falls für jedes  ein
ein 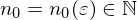 existiert mit
existiert mit 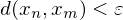 für alle
für alle 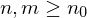 .
.Folgerung
1. Jede konvergente Folge aus
 ist eine Cauchy-Folge.
ist eine Cauchy-Folge.2. Jede Cachy-Folge ist beschränkt.
Def.: vollständig
 heißt vollständig, wenn jede Cauchy-Folge aus
heißt vollständig, wenn jede Cauchy-Folge aus  gegen einen Grenzwert in X konvergiert.
gegen einen Grenzwert in X konvergiert.Ein vollständiger normierter Raum heißt auch Banachraum.
Folgerung
 und
und 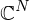 sind vollständig, d.h. sie sind Banachräume bzgl. jeder Norm.
sind vollständig, d.h. sie sind Banachräume bzgl. jeder Norm.Satz über Vollständigkeit von 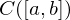
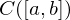
Der unendlichdimensionale normierte Raum 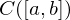 ist vollständig bezüglich
ist vollständig bezüglich
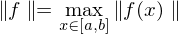
(Maximum- bzw. Supremumnorm auf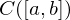 .
.
Bemerkungen
1. Bezüglich der durch das Skalarprodukt
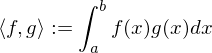
bestimmten Norm ist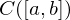 nicht vollständig.
nicht vollständig.
2. Konvergenz bezüglich des Maximum heißt auch gleichmäßige Konvergenz der Funktionenfolge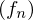 im Gegensatz zur punktweisen Konvergenz der Funktionenfolge
im Gegensatz zur punktweisen Konvergenz der Funktionenfolge 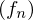 von
von

für jedes .
.
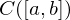 ist vollständig bezüglich
ist vollständig bezüglich 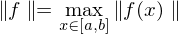
(Maximum- bzw. Supremumnorm auf
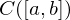 .
.Bemerkungen
1. Bezüglich der durch das Skalarprodukt
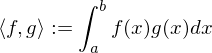
bestimmten Norm ist
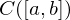 nicht vollständig.
nicht vollständig.2. Konvergenz bezüglich des Maximum heißt auch gleichmäßige Konvergenz der Funktionenfolge
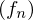 im Gegensatz zur punktweisen Konvergenz der Funktionenfolge
im Gegensatz zur punktweisen Konvergenz der Funktionenfolge 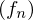 von
von 
für jedes
 .
.Def.: kompakt
Die Menge  heißt (folgen-)kompakt, wenn jede Folge aus
heißt (folgen-)kompakt, wenn jede Folge aus  eine konvergente Teilfolge mit Grenzwert in
eine konvergente Teilfolge mit Grenzwert in  besitzt.
besitzt.
Jede kompakte Menge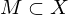 ist beschränkt und abgeschlossen bezüglich der Metrik
ist beschränkt und abgeschlossen bezüglich der Metrik 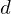 von
von 
 heißt (folgen-)kompakt, wenn jede Folge aus
heißt (folgen-)kompakt, wenn jede Folge aus  eine konvergente Teilfolge mit Grenzwert in
eine konvergente Teilfolge mit Grenzwert in  besitzt.
besitzt.Jede kompakte Menge
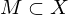 ist beschränkt und abgeschlossen bezüglich der Metrik
ist beschränkt und abgeschlossen bezüglich der Metrik 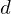 von
von 
Satz von Bolzano Weierstraß im 

Jede beschränkte Menge  des
des  besitzt einen Häufungspunkt.
besitzt einen Häufungspunkt.
 des
des  besitzt einen Häufungspunkt.
besitzt einen Häufungspunkt.Zusammenhang Kompaktheit und Beschränktheit
Im  und
und 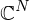 ist die Kompaktheit von
ist die Kompaktheit von  äquivalent zur Beschränktheit. In allgemeinen metrischen Räumen folgt aus Beschränktheit und Abgeschlossenheit nicht die Kompaktheit der Menge.
äquivalent zur Beschränktheit. In allgemeinen metrischen Räumen folgt aus Beschränktheit und Abgeschlossenheit nicht die Kompaktheit der Menge.
 und
und 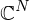 ist die Kompaktheit von
ist die Kompaktheit von  äquivalent zur Beschränktheit. In allgemeinen metrischen Räumen folgt aus Beschränktheit und Abgeschlossenheit nicht die Kompaktheit der Menge.
äquivalent zur Beschränktheit. In allgemeinen metrischen Räumen folgt aus Beschränktheit und Abgeschlossenheit nicht die Kompaktheit der Menge.Satz über die Stetigkeit der Grenzfunktion
Sei 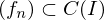 gleichmäßig konvergent gegen f, so ist
gleichmäßig konvergent gegen f, so ist 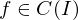 .
.
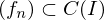 gleichmäßig konvergent gegen f, so ist
gleichmäßig konvergent gegen f, so ist 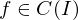 .
.Satz über die Vertauschbarkeit von Integration und Grenzwert
Sei 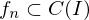 gleichmäßig konvergent gegen
gleichmäßig konvergent gegen  und
und 
für .
.
Dann gilt: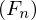 konvergiert gleichmäßig gegen F und
konvergiert gleichmäßig gegen F und
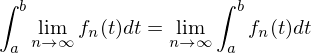
(genau dann, wenn ).
).
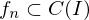 gleichmäßig konvergent gegen
gleichmäßig konvergent gegen  und
und 
für
 .
. Dann gilt:
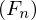 konvergiert gleichmäßig gegen F und
konvergiert gleichmäßig gegen F und 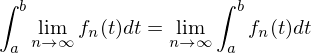
(genau dann, wenn
 ).
).Satz über die Vertauschbarkeit von Differentiation und Grenzwertbildung
Sei  und
und 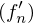 gleichmäßig konvergent gegen
gleichmäßig konvergent gegen 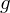 und
und
 für ein
für ein 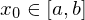 .
.
Dann konvergiert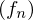 gleichmäßig gegen
gleichmäßig gegen  ,
,
wobei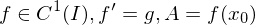 .
.
 und
und 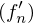 gleichmäßig konvergent gegen
gleichmäßig konvergent gegen 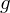 und
und für ein
für ein 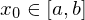 .
.Dann konvergiert
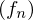 gleichmäßig gegen
gleichmäßig gegen  ,
,wobei
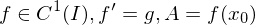 .
.Def.: gleichmäßige Konvergenz einer Funktionenreihe
Die Funktionenreihe
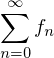
heißt gleichmäßig konvergent gegen , wenn die Funktionenfolge
, wenn die Funktionenfolge

gleichmäßig gegen konvergiert
konvergiert
(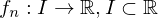 ).
).
Majorantenkriterium
Wenn für alle
für alle 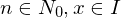 gilt und
gilt und

konvergiert, dann ist
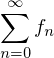
gleichmäßig konvergent auf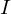 .
.
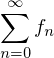
heißt gleichmäßig konvergent gegen
 , wenn die Funktionenfolge
, wenn die Funktionenfolge
gleichmäßig gegen
 konvergiert
konvergiert (
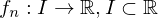 ).
).Majorantenkriterium
Wenn
 für alle
für alle 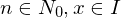 gilt und
gilt und 
konvergiert, dann ist
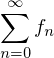
gleichmäßig konvergent auf
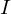 .
.Def.: Stetigkeit
 heißt stetig in
heißt stetig in  ,
, falls für jede Folge
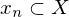 mit
mit
gilt:
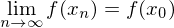 .
.(Äquivalent zum
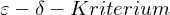 reeler Funktionen)
reeler Funktionen) heißt stetig auf
heißt stetig auf  , falls
, falls  stetig in allen
stetig in allen 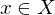 ist.
ist. 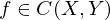
Eine bijektive Abbildung
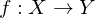 heißt Homöomophismus, falls
heißt Homöomophismus, falls  und
und  stetig sind.
stetig sind.Die Hintereinanderausführung stetiger Funktionen ist wieder stetig.
Def.: zusammenhängende Menge
 ist genau dann zusammenhängend, wenn für alle
ist genau dann zusammenhängend, wenn für alle  ein
ein  existiert mit
existiert mit 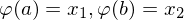 und
und  für alle
für alle  .
.Eine nichtleere, offene und zusammenhängende Menge heißt Gebiet.
Sei
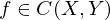 und
und 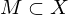 eine zusammenhängende Menge. Dann ist auch
eine zusammenhängende Menge. Dann ist auch  zusammenhängend.
zusammenhängend.Def.: Kontraktion
Sei  ein metrischer Raum und
ein metrischer Raum und  .
.
Gilt mit einer Konstanten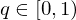 :
:
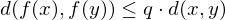
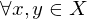
so heißt eine Kontraktion oder kontraktive Selbstabbildung auf X.
eine Kontraktion oder kontraktive Selbstabbildung auf X.
q heißt Kontraktionskonstante von .
.
Jeder Kontraktion ist stetig.
ist stetig.
 ein metrischer Raum und
ein metrischer Raum und  .
.Gilt mit einer Konstanten
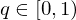 :
: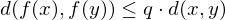
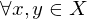
so heißt
 eine Kontraktion oder kontraktive Selbstabbildung auf X.
eine Kontraktion oder kontraktive Selbstabbildung auf X.q heißt Kontraktionskonstante von
 .
.Jeder Kontraktion
 ist stetig.
ist stetig.Banachscher Fixpunktsatz
Sei  ein vollständig metrischer Raum und
ein vollständig metrischer Raum und  eine Kontraktion auf
eine Kontraktion auf  .
.
Dann besitzt in
in  genau einen Fixpunkt
genau einen Fixpunkt 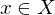 .
.
Dieser ergibt sich durch sukzessive Approximationen:
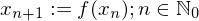
mit beliebigem Startpunkt .
.
Bemerkung
Der Fixpunktsatz gilt auch, wenn ersetzt wird durch ein abgeschlossenes
ersetzt wird durch ein abgeschlossenes 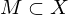 .
.
 ein vollständig metrischer Raum und
ein vollständig metrischer Raum und  eine Kontraktion auf
eine Kontraktion auf  .
. Dann besitzt
 in
in  genau einen Fixpunkt
genau einen Fixpunkt 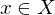 .
.Dieser ergibt sich durch sukzessive Approximationen:
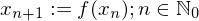
mit beliebigem Startpunkt
 .
.Bemerkung
Der Fixpunktsatz gilt auch, wenn
 ersetzt wird durch ein abgeschlossenes
ersetzt wird durch ein abgeschlossenes 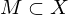 .
.Newton-Verfahren
Das Newton-Verfahren dient der angenäherten Berechnung einer Lösung von  für reelle Funktionen
für reelle Funktionen  .
.
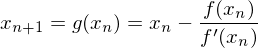
Geometrische Deutung
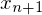 ensteht durch Schnittpunkt einer Tangente an einem beliebigen Punkt mit der x-Achse.
ensteht durch Schnittpunkt einer Tangente an einem beliebigen Punkt mit der x-Achse.
Tangente:

 für reelle Funktionen
für reelle Funktionen  .
.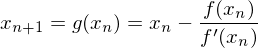
Geometrische Deutung
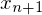 ensteht durch Schnittpunkt einer Tangente an einem beliebigen Punkt mit der x-Achse.
ensteht durch Schnittpunkt einer Tangente an einem beliebigen Punkt mit der x-Achse.Tangente:

Def.: Partielle Ableitung
 sei ein Gebiet.
sei ein Gebiet.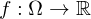 ist reellwertige oder skalare Funktion.
ist reellwertige oder skalare Funktion.Dann definiert man die partielle Ableitung von
 in
in 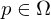 :
:
für
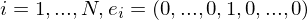 (1 an der i-ten Stelle).
(1 an der i-ten Stelle).Geometrische Deutung
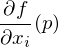 liefert den Anstieg der Fläche y = f(x) in
liefert den Anstieg der Fläche y = f(x) in 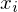 -Richtung und damit den Anstieg der Tangentialebene T.
-Richtung und damit den Anstieg der Tangentialebene T.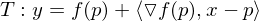
Satz von Schwarz
Sind alle partiellen Ableitungen 2. Ordnung für  in
in  vorhanden und in
vorhanden und in 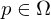 stetig, so gilt:
stetig, so gilt:
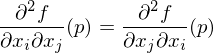
für
Verallgemeinerung
Für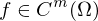 sind die partiellen Ableitungen bis Ordnung
sind die partiellen Ableitungen bis Ordnung 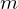 unabhängig von der Differentiationsreihenfolge.
unabhängig von der Differentiationsreihenfolge.
 in
in  vorhanden und in
vorhanden und in 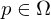 stetig, so gilt:
stetig, so gilt: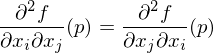
für

Verallgemeinerung
Für
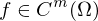 sind die partiellen Ableitungen bis Ordnung
sind die partiellen Ableitungen bis Ordnung 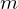 unabhängig von der Differentiationsreihenfolge.
unabhängig von der Differentiationsreihenfolge.Def.: Toatales Differential
Sei 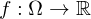 und
und  ein Gebiet des
ein Gebiet des  .
.
Dann heißt (total) differenzierbar in
(total) differenzierbar in 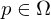 , falls
, falls
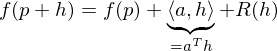
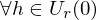
mit einem Vektor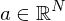 und
und 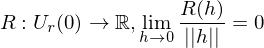
Wir nennen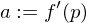 Ableitung von
Ableitung von  in
in  .
.
Folgerung
(1) Ist (total) differenzierbar in
(total) differenzierbar in  , so ist
, so ist  auch stetig in
auch stetig in  .
. 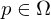
(2) Ist in
in  (total) differenziebar, dann auch partiell.
(total) differenziebar, dann auch partiell.
(3) Ist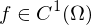 , so ist
, so ist  (total) differenzierbar in
(total) differenzierbar in  .
.
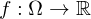 und
und  ein Gebiet des
ein Gebiet des  .
.Dann heißt
 (total) differenzierbar in
(total) differenzierbar in 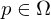 , falls
, falls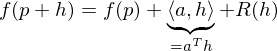
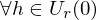
mit einem Vektor
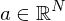 und
und 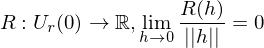
Wir nennen
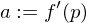 Ableitung von
Ableitung von  in
in  .
.Folgerung
(1) Ist
 (total) differenzierbar in
(total) differenzierbar in  , so ist
, so ist  auch stetig in
auch stetig in  .
. 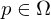
(2) Ist
 in
in  (total) differenziebar, dann auch partiell.
(total) differenziebar, dann auch partiell.(3) Ist
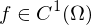 , so ist
, so ist  (total) differenzierbar in
(total) differenzierbar in  .
.Differenzierbarkeit von 


Dann ist
 differenzierbar in
differenzierbar in 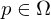 , falls jede Koordinatenfunktion
, falls jede Koordinatenfunktion 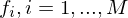 differenzierbar in
differenzierbar in  ist.
ist. ist genau dann in
ist genau dann in 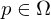 differenziebar, falls es eine lineare Abbildung
differenziebar, falls es eine lineare Abbildung 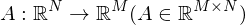
gibt mit
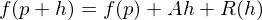
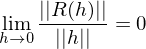
 heißt Ableitung von
heißt Ableitung von  in
in 
Jacobi Matrix
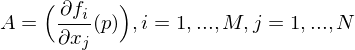
Def.: Vektorfeld
BSP
BSP
Ein Vektorfeld auf  ist eine Abbildung
ist eine Abbildung
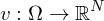

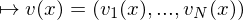
Speziell heißt ein
ein 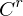 -Vektorfeld auf
-Vektorfeld auf  , falls
, falls  .
.
Integrabilitätsbedingungen
(1) Zwei Stammfunktionen zum Vektorfeld auf einem Gebiet
auf einem Gebiet  unterscheiden sich nur durch eine Konstante.
unterscheiden sich nur durch eine Konstante.
(2) Dem Vektorfeld kann eine Differentialform zugeordnet werden:
kann eine Differentialform zugeordnet werden:

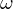 ist exakt wenn gilt:
ist exakt wenn gilt:
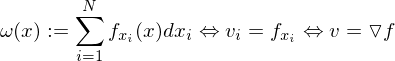
(3) Integrabilitätsbedingung
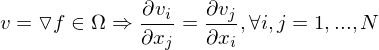
 ist eine Abbildung
ist eine Abbildung 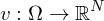

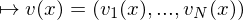
Speziell heißt
 ein
ein 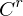 -Vektorfeld auf
-Vektorfeld auf  , falls
, falls  .
.Integrabilitätsbedingungen
(1) Zwei Stammfunktionen zum Vektorfeld
 auf einem Gebiet
auf einem Gebiet  unterscheiden sich nur durch eine Konstante.
unterscheiden sich nur durch eine Konstante.(2) Dem Vektorfeld
 kann eine Differentialform zugeordnet werden:
kann eine Differentialform zugeordnet werden:
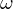 ist exakt wenn gilt:
ist exakt wenn gilt: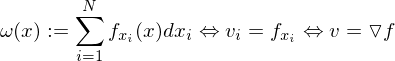
(3) Integrabilitätsbedingung
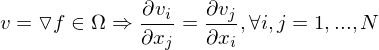
Vektorprodukt
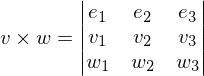
Eigenschaften
(1) Das Vektorprodukt ist linear in jedem Faktor.
(2) Das Vekotorprodkt ist schiefsymmetrisch:

(3)
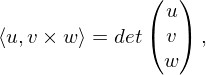
 sind Zeilenvektoren.
sind Zeilenvektoren.Gradient, Divergenz und Rotation
Gradient
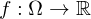

Punkte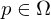 mit
mit 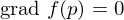 heißen stationäre oder kritische Punkte.
heißen stationäre oder kritische Punkte.
Divergenz
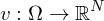
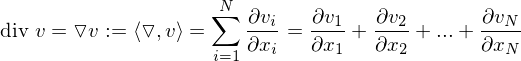
Ist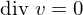 , so heißt das Vektorfeld quellenfrei.
, so heißt das Vektorfeld quellenfrei.
Rotation

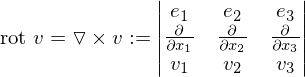
Ist , so heißt das Vektorfeld wirbelfrei.
, so heißt das Vektorfeld wirbelfrei.
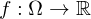

Punkte
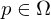 mit
mit 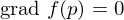 heißen stationäre oder kritische Punkte.
heißen stationäre oder kritische Punkte.Divergenz
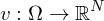
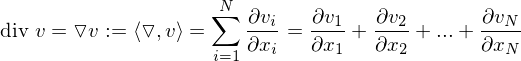
Ist
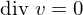 , so heißt das Vektorfeld quellenfrei.
, so heißt das Vektorfeld quellenfrei.Rotation

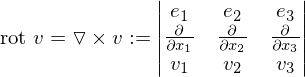
Ist
 , so heißt das Vektorfeld wirbelfrei.
, so heißt das Vektorfeld wirbelfrei.lokale Extrema
Notwendige Bedingung
Hat in
in 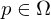 ein lokales Minimum, so gilt
ein lokales Minimum, so gilt
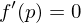
und
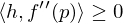
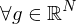
Hinreichende Bedinung
Gilt in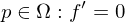 und ist
und ist 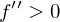
 dann hat
dann hat  in
in  ein lokales Minimum.
ein lokales Minimum.
Hat
 in
in 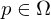 ein lokales Minimum, so gilt
ein lokales Minimum, so gilt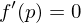
und
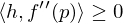
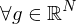
Hinreichende Bedinung
Gilt in
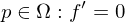 und ist
und ist 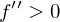
 dann hat
dann hat  in
in  ein lokales Minimum.
ein lokales Minimum.Trägheitssatz von Sylvester
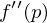 ist positiv definit
ist positiv definit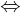 Alle Eigenwerte von
Alle Eigenwerte von  sind positiv
sind positiv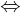 Alle Hauptminoren der Matrix
Alle Hauptminoren der Matrix  sind positiv (Determinante > 0)
sind positiv (Determinante > 0)Hauptsatz über implizite Funktionen
BSP
BSP
Sei 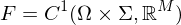 .
.
Für ein gelte
gelte
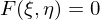 sowie die Auflösebedinung
sowie die Auflösebedinung
 .
.
Dann gibt es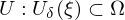 und
und  , so dass genau eine stetige Funktion
, so dass genau eine stetige Funktion
 existiert mit
existiert mit  und
und  .
.
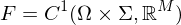 .
. Für ein
 gelte
gelte 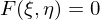 sowie die Auflösebedinung
sowie die Auflösebedinung .
.Dann gibt es
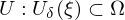 und
und  , so dass genau eine stetige Funktion
, so dass genau eine stetige Funktion existiert mit
existiert mit  und
und  .
.Def.: Diffeomorphismus
Seien 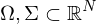 Gebiete.
Gebiete.
Eine Abbildung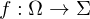 heißt Diffeomorphismus, wenn
heißt Diffeomorphismus, wenn  bijektiv ist und
bijektiv ist und 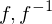 differenzierbar sind.
differenzierbar sind.
 heißt
heißt 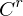 -Diffeomorphismus, falls
-Diffeomorphismus, falls 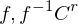 -Abbildungen sind.
-Abbildungen sind.
Man nennt einen lokalen Diffeomorphismus falls es zu jedem
einen lokalen Diffeomorphismus falls es zu jedem 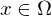 offene Mengen
offene Mengen 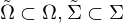 gibt, so dass die Einschränkung
gibt, so dass die Einschränkung 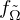 von
von  auf
auf 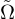 ein Diffeomorphismus von
ein Diffeomorphismus von 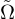 auf
auf 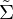 ist.
ist.
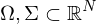 Gebiete.
Gebiete.Eine Abbildung
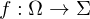 heißt Diffeomorphismus, wenn
heißt Diffeomorphismus, wenn  bijektiv ist und
bijektiv ist und 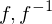 differenzierbar sind.
differenzierbar sind. heißt
heißt 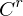 -Diffeomorphismus, falls
-Diffeomorphismus, falls 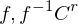 -Abbildungen sind.
-Abbildungen sind.Man nennt
 einen lokalen Diffeomorphismus falls es zu jedem
einen lokalen Diffeomorphismus falls es zu jedem 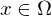 offene Mengen
offene Mengen 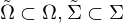 gibt, so dass die Einschränkung
gibt, so dass die Einschränkung 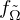 von
von  auf
auf 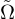 ein Diffeomorphismus von
ein Diffeomorphismus von 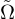 auf
auf 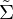 ist.
ist.Lösungsmannigfaltigkeit
Die Lösungsmenge
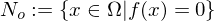
heißt Lösungsmannigfaltigkeit, falls

maximalen Rang hat
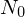 hat die Dimension
hat die Dimension 
Die Niveaumenge hat die Dimension 1
hat die Dimension 1
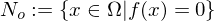
heißt Lösungsmannigfaltigkeit, falls

maximalen Rang hat
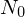 hat die Dimension
hat die Dimension 
Die Niveaumenge
 hat die Dimension 1
hat die Dimension 1Integralkriterium für unendliche Reihen
Sei  positiv und stetig auf
positiv und stetig auf  sowie monoton fallend.
sowie monoton fallend.
Dann ist das Konvergenzverhalten von
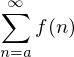
und
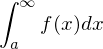
gleich (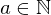 )
)
 positiv und stetig auf
positiv und stetig auf  sowie monoton fallend.
sowie monoton fallend.Dann ist das Konvergenzverhalten von
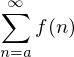
und
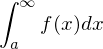
gleich (
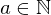 )
)Absolute Integrierbarkeit
Sei 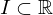 ein offenes oder halboffenes Intervall. Dann heißt
ein offenes oder halboffenes Intervall. Dann heißt  auf
auf 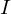 absolut integrierbar, falls
absolut integrierbar, falls
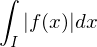
konvergiert oder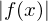 auf
auf 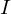 (uneigentlich) Riemann-integrierbar ist.
(uneigentlich) Riemann-integrierbar ist.
Aus absoluter Konvergenz folgt Konvergenz.
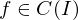 ist absolut integrierbar genau dann, wenn eine der beiden folgenden Bedingungen erfüllt ist:
ist absolut integrierbar genau dann, wenn eine der beiden folgenden Bedingungen erfüllt ist:
1.Beschränktheitskriterium

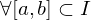
2. Majorantenkriterium
Es existiert eine positive Funktion mit
mit
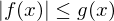
für alle und
und

konvergiert.
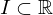 ein offenes oder halboffenes Intervall. Dann heißt
ein offenes oder halboffenes Intervall. Dann heißt  auf
auf 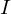 absolut integrierbar, falls
absolut integrierbar, falls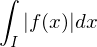
konvergiert oder
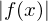 auf
auf 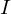 (uneigentlich) Riemann-integrierbar ist.
(uneigentlich) Riemann-integrierbar ist.Aus absoluter Konvergenz folgt Konvergenz.
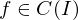 ist absolut integrierbar genau dann, wenn eine der beiden folgenden Bedingungen erfüllt ist:
ist absolut integrierbar genau dann, wenn eine der beiden folgenden Bedingungen erfüllt ist:1.Beschränktheitskriterium

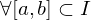
2. Majorantenkriterium
Es existiert eine positive Funktion
 mit
mit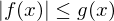
für alle
 und
und
konvergiert.
Def.: Parameterintegrale
BSP
BSP
Sei 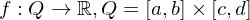
Existiert
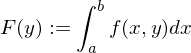
für alle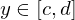 , so heißt
, so heißt 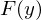 Parametrintegral.
Parametrintegral.
1. Ist , so existiert
, so existiert 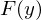 für jedes
für jedes 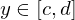 und ist stetig.
und ist stetig.
2. Sind
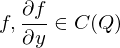 ,
,
so ist und
und
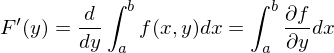
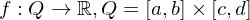
Existiert
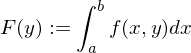
für alle
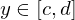 , so heißt
, so heißt 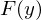 Parametrintegral.
Parametrintegral.1. Ist
 , so existiert
, so existiert 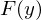 für jedes
für jedes 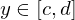 und ist stetig.
und ist stetig.2. Sind
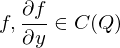 ,
,so ist
 und
und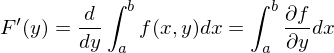
Def.: Kurve
Sei 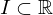 ein Intervall und
ein Intervall und  ein Gebiet.
ein Gebiet.
Dann heißt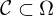 Kurve oder Weg, falls es eine stetige Abbildung
Kurve oder Weg, falls es eine stetige Abbildung
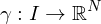
gibt mit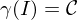 .
.
Man nennt eine
eine 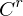 -Kurve, falls
-Kurve, falls
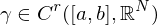
und reguläre Kurve, falls der Tangentenvektor
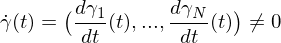
für alle .
.
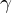 heißt Parametrisierung von
heißt Parametrisierung von  .
.
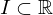 ein Intervall und
ein Intervall und  ein Gebiet.
ein Gebiet.Dann heißt
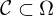 Kurve oder Weg, falls es eine stetige Abbildung
Kurve oder Weg, falls es eine stetige Abbildung 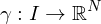
gibt mit
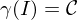 .
.Man nennt
 eine
eine 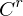 -Kurve, falls
-Kurve, falls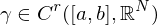
und reguläre Kurve, falls der Tangentenvektor
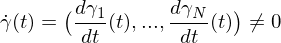
für alle
 .
.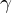 heißt Parametrisierung von
heißt Parametrisierung von  .
.Def.: Länge einer Kurve
Ist 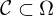 gegeben durch
gegeben durch
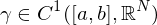 ,
,
so heißt
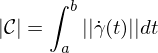
Länge der Kurve .
.
Bemerkung
Ist die Kurve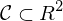 durch eine Funktion
durch eine Funktion  gegeben, so wählt man die Parametrisierung
gegeben, so wählt man die Parametrisierung
 .
.
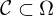 gegeben durch
gegeben durch 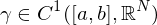 ,
, so heißt
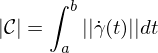
Länge der Kurve
 .
.Bemerkung
Ist die Kurve
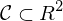 durch eine Funktion
durch eine Funktion  gegeben, so wählt man die Parametrisierung
gegeben, so wählt man die Parametrisierung  .
.Def.: Parametertransformation
Zwei 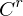 -Parametrisierungen von
-Parametrisierungen von 
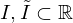 sind Intervalle, heißen äquivalent, wenn es einen
sind Intervalle, heißen äquivalent, wenn es einen 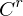 -Diffeomorphismus
-Diffeomorphismus  gibt, das heißt
gibt, das heißt  .
.
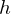 heißt Parametertransformation von
heißt Parametertransformation von  .
.
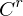 -Parametrisierungen von
-Parametrisierungen von 
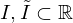 sind Intervalle, heißen äquivalent, wenn es einen
sind Intervalle, heißen äquivalent, wenn es einen 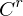 -Diffeomorphismus
-Diffeomorphismus  gibt, das heißt
gibt, das heißt  .
.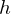 heißt Parametertransformation von
heißt Parametertransformation von  .
.Def.: vektorielles Bogenelement
Sei  ein Vektorfeld auf
ein Vektorfeld auf  und
und 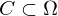 eine reguläre
eine reguläre 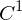 -Kurve mit Parametrisierung, so ist
-Kurve mit Parametrisierung, so ist

 ist vektorielles Bogenelement von
ist vektorielles Bogenelement von 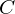 .
.
 ein Vektorfeld auf
ein Vektorfeld auf  und
und 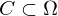 eine reguläre
eine reguläre 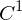 -Kurve mit Parametrisierung, so ist
-Kurve mit Parametrisierung, so ist
 ist vektorielles Bogenelement von
ist vektorielles Bogenelement von 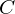 .
.Def.: Konservatives Vektorfeld
Das Vektorfeld  auf
auf  heißt konservativ in
heißt konservativ in  , wenn
, wenn

wegunaghängig ist für jede reguläre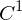 -Kurve
-Kurve 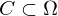 , das heißt wenn
, das heißt wenn 
nur von den Endpunkten von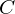 abhängt und nicht von deren Verlauf.
abhängt und nicht von deren Verlauf.
Ein Vektorfeld ist konservativ in
ist konservativ in 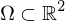 genau dann, wenn
genau dann, wenn  ein Potentialfeld in
ein Potentialfeld in  ist
ist
 auf
auf  heißt konservativ in
heißt konservativ in  , wenn
, wenn
wegunaghängig ist für jede reguläre
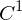 -Kurve
-Kurve 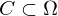 , das heißt wenn
, das heißt wenn 
nur von den Endpunkten von
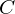 abhängt und nicht von deren Verlauf.
abhängt und nicht von deren Verlauf.Ein Vektorfeld
 ist konservativ in
ist konservativ in 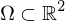 genau dann, wenn
genau dann, wenn  ein Potentialfeld in
ein Potentialfeld in  ist
istDef.: sternförmiges Gebiet
 heißt sternförmiges Gebiet, wenn es ein Zentrum
heißt sternförmiges Gebiet, wenn es ein Zentrum 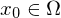 gibt, so dass für jedes
gibt, so dass für jedes 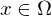 die Verbindungsgerade
die Verbindungsgerade 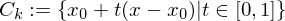 vollständig in
vollständig in  verläuft.
verläuft.Ist
 ein strnförmiges Gebiet und sind in
ein strnförmiges Gebiet und sind in  die Integrabilitätsbedingungen erfüllt, so besitzt das
die Integrabilitätsbedingungen erfüllt, so besitzt das 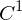 -Vektorfeld ein Potential in ganz
-Vektorfeld ein Potential in ganz  .
.Def.: Normalbereich
bez. der x-Achse
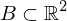 heißt Normalbereich bezüglich er x-Achse, wenn
heißt Normalbereich bezüglich er x-Achse, wenn
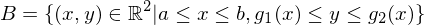
mit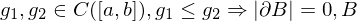 kompakt.
kompakt.
bez. der y-Achse
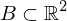 heißt Normalbereich bezüglich er y-Achse, wenn
heißt Normalbereich bezüglich er y-Achse, wenn
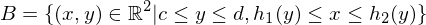
mit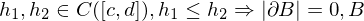 kompakt.
kompakt.
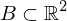 heißt Normalbereich bezüglich er x-Achse, wenn
heißt Normalbereich bezüglich er x-Achse, wenn 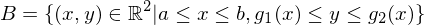
mit
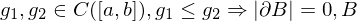 kompakt.
kompakt.bez. der y-Achse
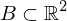 heißt Normalbereich bezüglich er y-Achse, wenn
heißt Normalbereich bezüglich er y-Achse, wenn 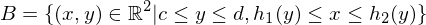
mit
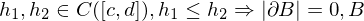 kompakt.
kompakt.Transformationssatz
Seien 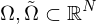 Gebiete und
Gebiete und  ein
ein 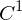 -Diffeomorphismus.
-Diffeomorphismus.
Dann gilt für jedes beschränkte mit
mit 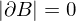 die Formel
die Formel
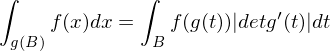
für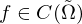
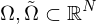 Gebiete und
Gebiete und  ein
ein 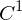 -Diffeomorphismus.
-Diffeomorphismus.Dann gilt für jedes beschränkte
 mit
mit 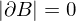 die Formel
die Formel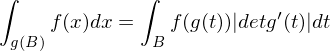
für
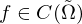
Gaußscher Integralsatz in der Ebene
Sei 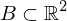 ein Normalbereich beider Achsen und
ein Normalbereich beider Achsen und  ein Gebiet sowie
ein Gebiet sowie 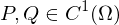 .
.
Dann gilt für positive Orientierung von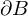 :
:


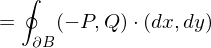

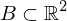 ein Normalbereich beider Achsen und
ein Normalbereich beider Achsen und  ein Gebiet sowie
ein Gebiet sowie 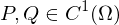 .
.Dann gilt für positive Orientierung von
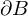 :
:

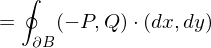

Kartensatzinfo:
Autor: Schokoholic007
Oberthema: Mathematik
Thema: Analysis
Veröffentlicht: 22.04.2010
Schlagwörter Karten:
Alle Karten (53)
keine Schlagwörter





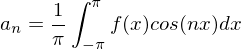

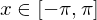 , so auch für alle
, so auch für alle 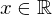
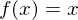 für
für 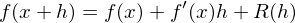
 und
und  falls
falls  differenzierbar.
differenzierbar.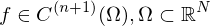 sei ein Gebiet
sei ein Gebiet .
.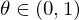 :
: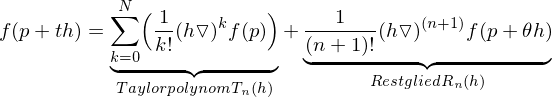
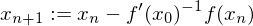

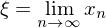 exisiert, so ist
exisiert, so ist 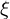 Fixpunkt der Abbildung
Fixpunkt der Abbildung  mit
mit 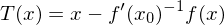 .
.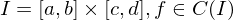 , so gilt
, so gilt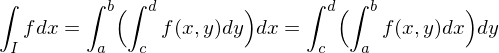
 so gilt:
so gilt: