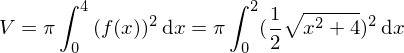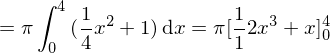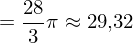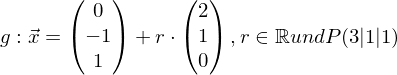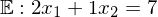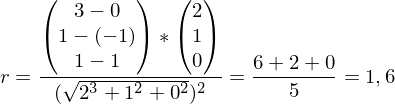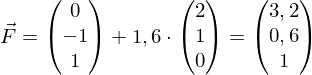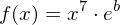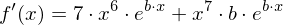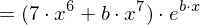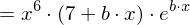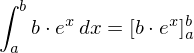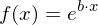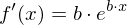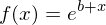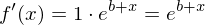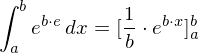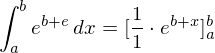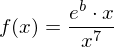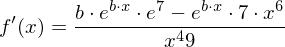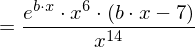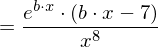A3 ...die Gleichung einer Tangente und einer Normale an den Graphen einer Funktion in einem Punkt bestimmen
Funktion : f(x) = - x² - x + 2
Die Gleichungen von Tangente und Normale sollen für den Punkt
P (2/ f(2)) blestimmt werden.
Vorüberlegung
Die Tangente ist eine Gerade mit der Gleichung
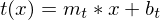 .
.
Die Normale ist eine dazu senkrechte Gerade mit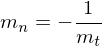 also mit der Gleichung
also mit der Gleichung 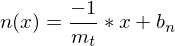
Die Steigung der Tangenten entspricht der Steigung des Graphen von f(x) im Punkt P.
Rechnung
f(x) = - x² - x + 2 -> f'(x) = - 2x - 1
Koordinaten des Punktes P( 2 / f(2) ):
f(2) = -2² - 2 + 2 = - 4 - 2 +2 = -4 -> P( 2/ - 4)
Steigung in P( 2 / - 4)
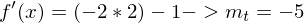 (Tangentensteigung)
(Tangentensteigung)
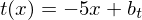
Die Tangente verläuft durch P(2 / - 4)
t(2) = - 4
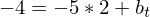
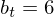
-> t(x) = - 5x + 6 ist die Tangente durch P ( 2 / - 4)
Normalengleichung
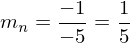
->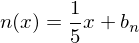
Die Normale verläuft durch den Punkt P( 2 / - 4 )
n(2) = - 4
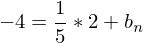
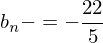
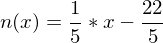
-> ist die Gleichung der Normalen die durch den Punkt P (2 / - 4) verläuft.
Die Gleichungen von Tangente und Normale sollen für den Punkt
P (2/ f(2)) blestimmt werden.
Vorüberlegung
Die Tangente ist eine Gerade mit der Gleichung
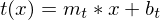 .
.Die Normale ist eine dazu senkrechte Gerade mit
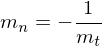 also mit der Gleichung
also mit der Gleichung 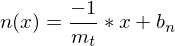
Die Steigung der Tangenten entspricht der Steigung des Graphen von f(x) im Punkt P.
Rechnung
f(x) = - x² - x + 2 -> f'(x) = - 2x - 1
Koordinaten des Punktes P( 2 / f(2) ):
f(2) = -2² - 2 + 2 = - 4 - 2 +2 = -4 -> P( 2/ - 4)
Steigung in P( 2 / - 4)
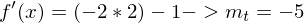 (Tangentensteigung)
(Tangentensteigung) 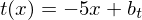
Die Tangente verläuft durch P(2 / - 4)
t(2) = - 4
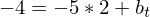
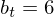
-> t(x) = - 5x + 6 ist die Tangente durch P ( 2 / - 4)
Normalengleichung
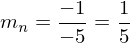
->
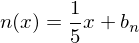
Die Normale verläuft durch den Punkt P( 2 / - 4 )
n(2) = - 4
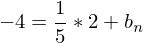
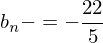
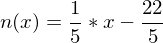
-> ist die Gleichung der Normalen die durch den Punkt P (2 / - 4) verläuft.
Tags:
Source: Alexander Barth
Source: Alexander Barth
C7 ... (LK) bestimmte Integrale mit den Verfahren der partitiellen Integration, der Substitutionsmethode und der Partitialbruchzerlegung berechnen.
Partitielle Integration
Für die partitielle Integration gilt :
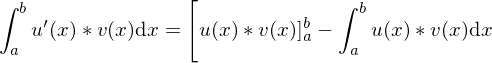
Substitutionsmethode
Gesucht sei die Stammfunktion von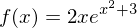 .
.
Also
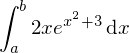
Dann ersetzen wir im Exponenten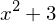 durch z
durch z
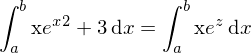
Anschließend formen wir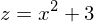 nach x um.
nach x um.
Jetzt können wir auch das x ersetzen.
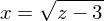
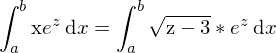
Jetzt müssen wir noch dx durch dz ersetzen.
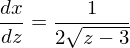
Nach Multiplikation mit dz erhalten wir
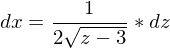
und können dx durch die ermittelte Funktion ersetzen
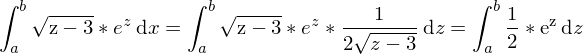
Dies lässt sich schon einfacher integrieren
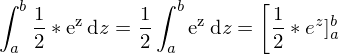
Nun müssen wir rücksubtitionieren
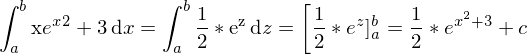
Beispiel Substitution
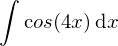
Substitution :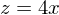
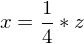
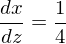
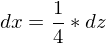
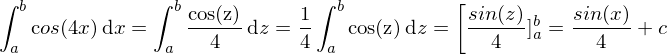
Partitialbruchzerlegung
Ermittelt werden soll die Stammfunktion von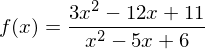
Also
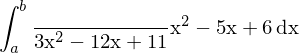
Zählergrad gleich Nennergrad oder größer, als erstes Polynomdivision
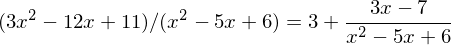
Daraus folgt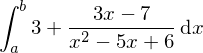
Zählergrad kleiner Nennergrad -> besitzt der Nenner Nullstellen
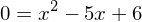 ->
-> 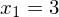 und
und 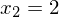
->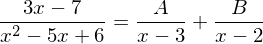
Den Term multiplizieren wir mit dem Hauptnenner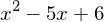
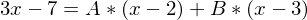
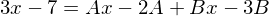
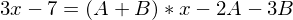
->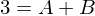 und
und 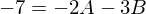
Nach lösen der zwei ermittelten Gleichungen ergeben sich für A und B folgende Werte:
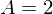 und
und 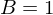
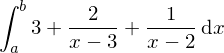
Nun kann man einfach die Stammfunktion ermitteln
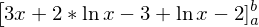
Für die partitielle Integration gilt :
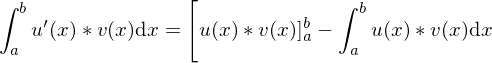
Substitutionsmethode
Gesucht sei die Stammfunktion von
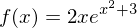 .
.Also
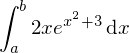
Dann ersetzen wir im Exponenten
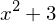 durch z
durch z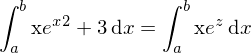
Anschließend formen wir
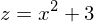 nach x um.
nach x um.Jetzt können wir auch das x ersetzen.
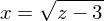
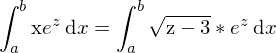
Jetzt müssen wir noch dx durch dz ersetzen.
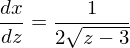
Nach Multiplikation mit dz erhalten wir
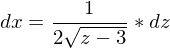
und können dx durch die ermittelte Funktion ersetzen
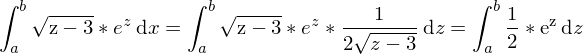
Dies lässt sich schon einfacher integrieren
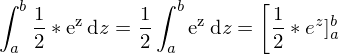
Nun müssen wir rücksubtitionieren
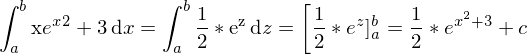
Beispiel Substitution
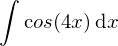
Substitution :
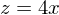
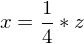
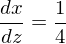
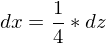
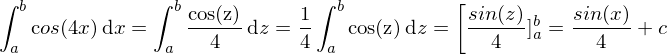
Partitialbruchzerlegung
Ermittelt werden soll die Stammfunktion von
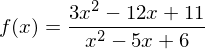
Also
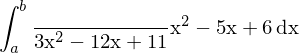
Zählergrad gleich Nennergrad oder größer, als erstes Polynomdivision
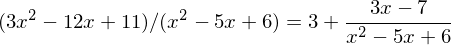
Daraus folgt
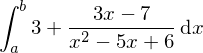
Zählergrad kleiner Nennergrad -> besitzt der Nenner Nullstellen
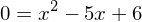 ->
-> 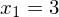 und
und 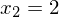
->
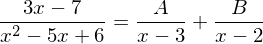
Den Term multiplizieren wir mit dem Hauptnenner
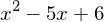
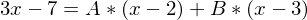
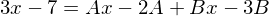
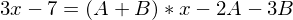
->
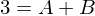 und
und 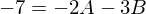
Nach lösen der zwei ermittelten Gleichungen ergeben sich für A und B folgende Werte:
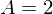 und
und 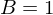
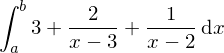
Nun kann man einfach die Stammfunktion ermitteln
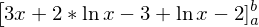
Tags:
Source: Alexander Barth
Source: Alexander Barth
A4 ...mittlere und momentane Änderungsraten in Anwendungssituationen (z.B. Geschwindigkeiten bei Bewegungsvorgängen) angeben und berechnen.
mittlere Änderungsrate
Für die mittlere Änderungsrate gilt :
Ämittlere=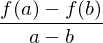
a und b geben, jeweils die Grenzen des Intervalles an, in dem die mittlere Änderungsrate bestimmt werden soll.
momentane Änderungsrate
Die momentane Änderungsrate wird durch die erste Ableitung einer Funktion angegeben.
Ämomentan =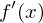
Für die mittlere Änderungsrate gilt :
Ämittlere=
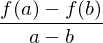
a und b geben, jeweils die Grenzen des Intervalles an, in dem die mittlere Änderungsrate bestimmt werden soll.
momentane Änderungsrate
Die momentane Änderungsrate wird durch die erste Ableitung einer Funktion angegeben.
Ämomentan =
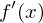
Tags:
Source: Alexander Barth
Source: Alexander Barth
Das Volumen von Rotationskörpern berechnen und die erforderlichen Berandungsfunktionen für reale rotationssymmetrische Körper modellieren.
Rotation um die x-Achse:
Rotation um die x-Achse:
Satz: Ist die Funktion f auf dem Intervall 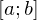 stetig, so entsteht bei Rotation der Fläche zwischen dem Graphen von f und der x-Achse über
stetig, so entsteht bei Rotation der Fläche zwischen dem Graphen von f und der x-Achse über 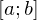 ein Körper mit dem Volumen:
ein Körper mit dem Volumen:
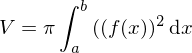
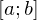 stetig, so entsteht bei Rotation der Fläche zwischen dem Graphen von f und der x-Achse über
stetig, so entsteht bei Rotation der Fläche zwischen dem Graphen von f und der x-Achse über 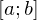 ein Körper mit dem Volumen:
ein Körper mit dem Volumen: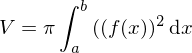
Das Volumen von Rotationskörpern berechnen und die erforderlichen Berandungsfunktionen für reale rotationssymmetrische Körper modellieren.
Rotation um die y-Achse:
Rotation um die y-Achse:
Satz: Ist die Funktion stetig und umkehrbar mit der Umkehrfunktion 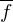 , so entsteht bei Rotation der Fläche zwischen dem Graphen von
, so entsteht bei Rotation der Fläche zwischen dem Graphen von  , der y-Achse und den Geraden mit den Gleichungen
, der y-Achse und den Geraden mit den Gleichungen 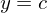 und
und 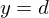 ein Rotationskörper mit dem Volumen:
ein Rotationskörper mit dem Volumen:
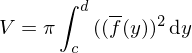
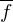 , so entsteht bei Rotation der Fläche zwischen dem Graphen von
, so entsteht bei Rotation der Fläche zwischen dem Graphen von  , der y-Achse und den Geraden mit den Gleichungen
, der y-Achse und den Geraden mit den Gleichungen 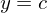 und
und 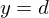 ein Rotationskörper mit dem Volumen:
ein Rotationskörper mit dem Volumen: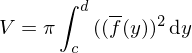
D1: Definitionslücken bestimmen und feststellen, ob diese behebbar sind oder nicht, und im zweiten Fall die Gleichung der zugehörigen senkrechten Asymptote angeben.
Bestimmung von Definitionslücken:
Eine gebrochenrationale Funktion f ist der Quotient aus zwei ganzrationalen Funktionen z und n. Es gilt also:
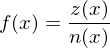 Da die Teilbarkeit durch 0 auszuschließen ist, ist der Definitionsbereich gebrochenrationaler Funktionen durch die Nullstellen des Nennerpolynoms eingeschränkt. Hat das Nennerpolynom keine Nullstellen so ist D=R.
Da die Teilbarkeit durch 0 auszuschließen ist, ist der Definitionsbereich gebrochenrationaler Funktionen durch die Nullstellen des Nennerpolynoms eingeschränkt. Hat das Nennerpolynom keine Nullstellen so ist D=R.
Zur Bestimmung der Nullstellen sollten zuerst Nenner und Zähler soweit wie möglich faktorisiert werden. Dazu dienen das Ausklammern, Binomische Formeln sowie die Polynomdivision.
Eine gebrochenrationale Funktion f ist der Quotient aus zwei ganzrationalen Funktionen z und n. Es gilt also:
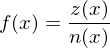 Da die Teilbarkeit durch 0 auszuschließen ist, ist der Definitionsbereich gebrochenrationaler Funktionen durch die Nullstellen des Nennerpolynoms eingeschränkt. Hat das Nennerpolynom keine Nullstellen so ist D=R.
Da die Teilbarkeit durch 0 auszuschließen ist, ist der Definitionsbereich gebrochenrationaler Funktionen durch die Nullstellen des Nennerpolynoms eingeschränkt. Hat das Nennerpolynom keine Nullstellen so ist D=R.Zur Bestimmung der Nullstellen sollten zuerst Nenner und Zähler soweit wie möglich faktorisiert werden. Dazu dienen das Ausklammern, Binomische Formeln sowie die Polynomdivision.
D1: Definitionslücken bestimmen und feststellen, ob diese behebbar sind oder nicht, und im zweiten Fall die Gleichung der zugehörigen senkrechten Asymptote angeben.
Hebbare/ Nicht- hebbare Lücken:
Hat das Zählerpolynom bei der Definitionslücke x₀ eine Nullstelle, d.h. z(x) strebt für x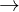 x₀ gegen 0, so liegt eine stetig behebbare Lücke vor. Sie ist auch daran zu erkennen, dass es sowohl im Nenner als auch im Zähler einen Linearfaktor mit gleichem Wert gibt und es gilt:
x₀ gegen 0, so liegt eine stetig behebbare Lücke vor. Sie ist auch daran zu erkennen, dass es sowohl im Nenner als auch im Zähler einen Linearfaktor mit gleichem Wert gibt und es gilt:
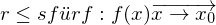
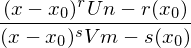
Bsp.: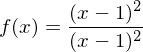
Durch Faktorisieren und anschließendem Kürzen mit (x- x₀) kann der Verlauf des Graphen g der Funktion f in der Nähe der Definitionslücke bestimmt werden. Die Funktion f lässt sich damit an der Stelle x₀ stetig fortsetzen.
Hat das Zählerpolynom bei der Definitionslücke x₀ eine Nullstelle, d.h. z(x) strebt für x
 x₀ gegen 0, so liegt eine stetig behebbare Lücke vor. Sie ist auch daran zu erkennen, dass es sowohl im Nenner als auch im Zähler einen Linearfaktor mit gleichem Wert gibt und es gilt:
x₀ gegen 0, so liegt eine stetig behebbare Lücke vor. Sie ist auch daran zu erkennen, dass es sowohl im Nenner als auch im Zähler einen Linearfaktor mit gleichem Wert gibt und es gilt: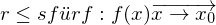
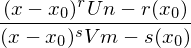
Bsp.:
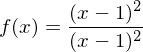
Durch Faktorisieren und anschließendem Kürzen mit (x- x₀) kann der Verlauf des Graphen g der Funktion f in der Nähe der Definitionslücke bestimmt werden. Die Funktion f lässt sich damit an der Stelle x₀ stetig fortsetzen.
D1: Definitionslücken bestimmen und feststellen, ob diese behebbar sind oder nicht, und im zweiten Fall die Gleichung der zugehörigen senkrechten Asymptote angeben.
Hat das Zählerpolynom bei der Definitionslücke x₀ keine Nullstelle, d.h. z(x) strebt für 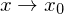 gegen eine von null verschiedene reelle Zahl, so liegt eine Unendlichkeitsstelle(Polstelle) vor. Sie ist auch daran zu erkennen, dass gilt:
gegen eine von null verschiedene reelle Zahl, so liegt eine Unendlichkeitsstelle(Polstelle) vor. Sie ist auch daran zu erkennen, dass gilt:
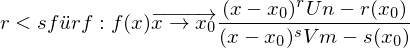
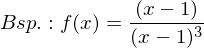
Hierbei ist im Weiteren noch die Unterscheidung zwischen einer Polstelle mit Vorzeichenwechsel (VZW) oder einer Polstelle ohne VZW zu treffen.
Dazu subtrahiert man den Grad des Linearfaktors des Nenners (s) mit dem Grad des Linearfaktors des Zählers (r). Ergibt sich aus dieser Subtraktion (s-r) eine gerade Zahl, so handelt es sich um eine Polstelle ohne VZW. Ergibt sich aus dieser Subtraktion (s-r) eine gerade Zahl, so handelt es sich um eine Polstelle mit VZW.
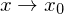 gegen eine von null verschiedene reelle Zahl, so liegt eine Unendlichkeitsstelle(Polstelle) vor. Sie ist auch daran zu erkennen, dass gilt:
gegen eine von null verschiedene reelle Zahl, so liegt eine Unendlichkeitsstelle(Polstelle) vor. Sie ist auch daran zu erkennen, dass gilt: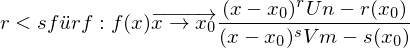
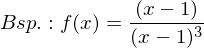
Hierbei ist im Weiteren noch die Unterscheidung zwischen einer Polstelle mit Vorzeichenwechsel (VZW) oder einer Polstelle ohne VZW zu treffen.
Dazu subtrahiert man den Grad des Linearfaktors des Nenners (s) mit dem Grad des Linearfaktors des Zählers (r). Ergibt sich aus dieser Subtraktion (s-r) eine gerade Zahl, so handelt es sich um eine Polstelle ohne VZW. Ergibt sich aus dieser Subtraktion (s-r) eine gerade Zahl, so handelt es sich um eine Polstelle mit VZW.
D1: Definitionslücken bestimmen und feststellen, ob diese behebbar sind oder nicht, und im zweiten Fall die Gleichung der zugehörigen senkrechten Asymptote angeben.
Gleichung einer senkrechten Asymptote:
Die Gleichung einer senkrechten Asymptote ergibt sich aus der Nullstelle des Nenners einer gebrochenrationalen Funktion. An der Stelle x₀, an der die Nennerfunktion eine Nullstelle hat, liegt die senkrechte Asymptote des Graphen g der Funktion f, so lange Zähler und Nenner nicht an der gleichen Stelle gleich null werden.
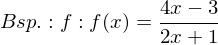
Es ist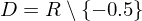 . Der Zähler wird an der Stelle
. Der Zähler wird an der Stelle 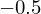 nicht null. Somit ist die senkrechte Asymptote die Gerade mit der Gleichung
nicht null. Somit ist die senkrechte Asymptote die Gerade mit der Gleichung 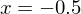
Die Gleichung einer senkrechten Asymptote ergibt sich aus der Nullstelle des Nenners einer gebrochenrationalen Funktion. An der Stelle x₀, an der die Nennerfunktion eine Nullstelle hat, liegt die senkrechte Asymptote des Graphen g der Funktion f, so lange Zähler und Nenner nicht an der gleichen Stelle gleich null werden.
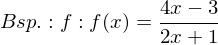
Es ist
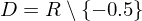 . Der Zähler wird an der Stelle
. Der Zähler wird an der Stelle 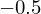 nicht null. Somit ist die senkrechte Asymptote die Gerade mit der Gleichung
nicht null. Somit ist die senkrechte Asymptote die Gerade mit der Gleichung 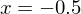
G2: Geraden auf ihre gegenseitige Lage untersuchen und möglicherweise vorhandene Schnittpunkte bestimmen. Beispiele:
Als Beispiel für zwei Geraden sei gegeben: Gerade 1 mit 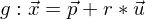 und Gerade 2 mit
und Gerade 2 mit 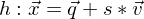
Zu Fall a)
Zwei Geraden sind echt parallel, wenn ihre Richtungsvektoren und
und  linear abhängig sind und ein Richtungsvektor (entweder
linear abhängig sind und ein Richtungsvektor (entweder  oder
oder 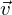 ) linear unabhängig zur Differenz der Aufpunktvektoren (
) linear unabhängig zur Differenz der Aufpunktvektoren (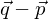 )ist.
)ist.
Zu Fall b)
Zwei Geraden sind echt parallel, wenn ihre Richtungsvektoren und
und  linear abhängig sind und ein Richtungsvektor (entweder
linear abhängig sind und ein Richtungsvektor (entweder  und
und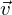 ) linear abhängig zur Differenz der Aufpunktvektoren (
) linear abhängig zur Differenz der Aufpunktvektoren (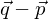 ) ist.
) ist.
Zu Fall c)
Zwei Geraden schneiden sich, ihre Richtungsvektoren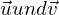 linear unabhängig sind und beide Richtungsvektoren
linear unabhängig sind und beide Richtungsvektoren  und
und  linear abhängig zur Differenz der Aufpunktvektoren (
linear abhängig zur Differenz der Aufpunktvektoren (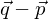 ) sind.
) sind.
Zu Fall d)
Zwei Geraden sind windschief, wenn sowohl Richtungsvektoren und
und  linear unabhängig sind, als auch beide Richtungsvektoren
linear unabhängig sind, als auch beide Richtungsvektoren  und
und  linear unabhängig zur Differenz der Aufpunktvektoren (
linear unabhängig zur Differenz der Aufpunktvektoren (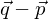 ) sind.
) sind.
g und h schneiden sich in einem Punkt, wenn die Vektorgleichung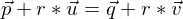 genau eine Lösung (r₀, t₀) hat.
genau eine Lösung (r₀, t₀) hat.
g und h sind identisch, wenn die Vektorgleichung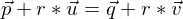 unendlich viele Lösungen hat.
unendlich viele Lösungen hat.
g und h haben keinen gemeinsamen Punkt, wenn die Vektorgleichung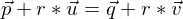 keine Lösung hat.
keine Lösung hat.
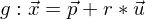 und Gerade 2 mit
und Gerade 2 mit 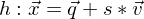
Zu Fall a)
Zwei Geraden sind echt parallel, wenn ihre Richtungsvektoren
 und
und  linear abhängig sind und ein Richtungsvektor (entweder
linear abhängig sind und ein Richtungsvektor (entweder  oder
oder 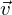 ) linear unabhängig zur Differenz der Aufpunktvektoren (
) linear unabhängig zur Differenz der Aufpunktvektoren (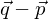 )ist.
)ist. Zu Fall b)
Zwei Geraden sind echt parallel, wenn ihre Richtungsvektoren
 und
und  linear abhängig sind und ein Richtungsvektor (entweder
linear abhängig sind und ein Richtungsvektor (entweder  und
und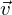 ) linear abhängig zur Differenz der Aufpunktvektoren (
) linear abhängig zur Differenz der Aufpunktvektoren (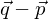 ) ist.
) ist.Zu Fall c)
Zwei Geraden schneiden sich, ihre Richtungsvektoren
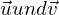 linear unabhängig sind und beide Richtungsvektoren
linear unabhängig sind und beide Richtungsvektoren  und
und  linear abhängig zur Differenz der Aufpunktvektoren (
linear abhängig zur Differenz der Aufpunktvektoren (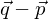 ) sind.
) sind.Zu Fall d)
Zwei Geraden sind windschief, wenn sowohl Richtungsvektoren
 und
und  linear unabhängig sind, als auch beide Richtungsvektoren
linear unabhängig sind, als auch beide Richtungsvektoren  und
und  linear unabhängig zur Differenz der Aufpunktvektoren (
linear unabhängig zur Differenz der Aufpunktvektoren (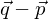 ) sind.
) sind.g und h schneiden sich in einem Punkt, wenn die Vektorgleichung
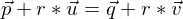 genau eine Lösung (r₀, t₀) hat.
genau eine Lösung (r₀, t₀) hat. g und h sind identisch, wenn die Vektorgleichung
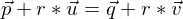 unendlich viele Lösungen hat.
unendlich viele Lösungen hat.g und h haben keinen gemeinsamen Punkt, wenn die Vektorgleichung
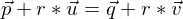 keine Lösung hat.
keine Lösung hat.G3: Parameterdarstellung für Ebenen aus drei Punkten ermitteln sowie überprüfen, ob ein Punkt auf einer gegebenen Ebene liegt (Punktprobe) und die Ergebnisse im Sachzusammenhang interpretieren.
Parameterdarstellung für Ebenen mit drei Punkten:
Die Gleichung einer Ebene E mit dem Stützvektor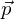 und den Spannvektoren
und den Spannvektoren 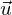 und
und 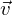 lautet:
lautet:
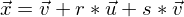 ; r, s ∈ R.
; r, s ∈ R.
E ist festgelegt durch die Punkte A, B und C:
Stützvektor: Ortsvektor von A
Spannvektoren: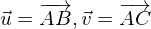
Punktprobe für den Punkt D:
Setzt man die Koordinaten für D in die Gleichung für E ein, erhält man ein LGS mit drei linearen Gleichungen für zwei Variablen r und s.
Aus zwei Gleichungen erhält man Werte für r und s; erfüllen diese Werte auch die dritte Gleichung liegt der Punkt D in E.
Die Gleichung einer Ebene E mit dem Stützvektor
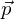 und den Spannvektoren
und den Spannvektoren 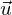 und
und 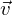 lautet:
lautet: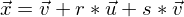 ; r, s ∈ R.
; r, s ∈ R.E ist festgelegt durch die Punkte A, B und C:
Stützvektor: Ortsvektor von A
Spannvektoren:
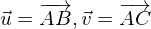
Punktprobe für den Punkt D:
Setzt man die Koordinaten für D in die Gleichung für E ein, erhält man ein LGS mit drei linearen Gleichungen für zwei Variablen r und s.
Aus zwei Gleichungen erhält man Werte für r und s; erfüllen diese Werte auch die dritte Gleichung liegt der Punkt D in E.
C3: Mittelwerte von kontinuierlich veränderten Größen mit der Integralrechnung berechnen.
Man nutzt Integralrechnung, um den Mittelwert M einer (stetigen) Funktion im Intervall [a;b] zu berechnen. Dazu teilt man das Integral in diesem Intervall durch die Differenz von b und a.
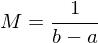
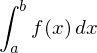
Beispiel: Berechnen Sie den durchschnittlichen Funktionswert der Funktion f mit:
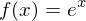 (x Element der reellen Zahlen)
(x Element der reellen Zahlen)
im Intervall von 0 bis 3.
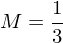
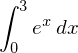
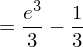
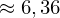
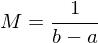
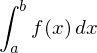
Beispiel: Berechnen Sie den durchschnittlichen Funktionswert der Funktion f mit:
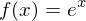 (x Element der reellen Zahlen)
(x Element der reellen Zahlen)im Intervall von 0 bis 3.
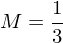
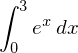
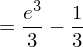
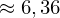
H2: Den Flächeninhalt eines Dreiecks und das Volumen eines Tetraeders nach elementaren Methoden bestimmen.
Der Flächeninhalt A eines Dreiecks ABC entspricht der Hälfte der Länge des Kreuzprodukts zweier Vektoren, die dieses Dreieck aufspannen.
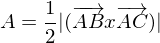
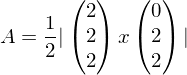
Beispiel: Gesucht ist der Flächeninhalt des Dreiecks ABC mit A(0/0/0), B(2/2/2) und C(0/2/2). Für A ergibt sich:
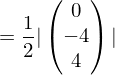
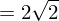
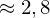
Ein Tetraeder ist eine Pyramide mit einer dreieckigen Grundfläche, bei der alle Seiten gleichlang sind.
Für das Volumen V gilt allgemein:
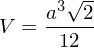
Als Beispiel nehmen wir einen Tetraeder ABCD mit den Eckpunkten A (1/1/1), B (1/0/0), C (0/1/0) und D (0/0/1).
Für das Volumen V ergibt sich:
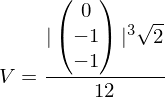
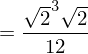
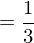
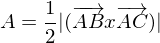
Beispiel: Gesucht ist der Flächeninhalt des Dreiecks ABC mit A(0/0/0), B(2/2/2) und C(0/2/2). Für A ergibt sich:

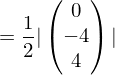
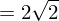
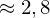
Ein Tetraeder ist eine Pyramide mit einer dreieckigen Grundfläche, bei der alle Seiten gleichlang sind.
Für das Volumen V gilt allgemein:
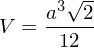
Als Beispiel nehmen wir einen Tetraeder ABCD mit den Eckpunkten A (1/1/1), B (1/0/0), C (0/1/0) und D (0/0/1).
Für das Volumen V ergibt sich:
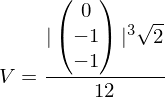
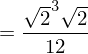
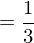
H3: Den Abstand eines Punktes von einer Ebene berechnen.
Der Abstand d eines Punktes Q zur Ebene E (mit dem Punkt P und dem Normalvektor 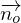 (Länge = 1LE)) lässt sich am einfachsten mit der HNF (Hesse'sche Normalenform) berechnen.
(Länge = 1LE)) lässt sich am einfachsten mit der HNF (Hesse'sche Normalenform) berechnen.
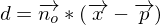
Beispiel: Welchen Abstand hat Q (5/3/1) zur -Ebene?
-Ebene?
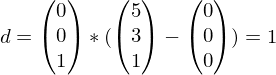
Hinweis: Auch andere Methoden, wie das Benutzen einer zu E senkrechten Geraden durch Q, um den zu Q nächsten Punkt in E zu finden, können benutzt werden.
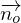 (Länge = 1LE)) lässt sich am einfachsten mit der HNF (Hesse'sche Normalenform) berechnen.
(Länge = 1LE)) lässt sich am einfachsten mit der HNF (Hesse'sche Normalenform) berechnen.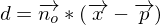
Beispiel: Welchen Abstand hat Q (5/3/1) zur
 -Ebene?
-Ebene?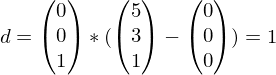
Hinweis: Auch andere Methoden, wie das Benutzen einer zu E senkrechten Geraden durch Q, um den zu Q nächsten Punkt in E zu finden, können benutzt werden.
H4: Den Abstand eines Punktes P zu einer Geraden g berechnen
Überlegung:
Zur Hilfe wird eine Ebene E, die orthogonal zur Geraden g ist und den Punkt P enthält aufgestellt. Der Richtungsvektor der Geraden wird dabei als Normalenvektor der Hilfsebene verwendet. Der Schnittpunkt von Gerade und Hilfsebene ist der Lotfußpunkt F. Die Länge der Strecke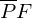 ist der gesuchte Abstand.
ist der gesuchte Abstand.
Die Ebene wird beschrieben durch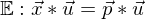 Der gemeinsame Punkt von g und
Der gemeinsame Punkt von g und 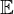 muss beide Gleichungen erfüllen, d.h. es muss gelten:
muss beide Gleichungen erfüllen, d.h. es muss gelten:
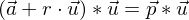
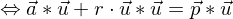
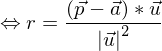
Dieser Wert für r wird in die Parameterdarstellung von g eingesetzt und man erhät die Koordinaten des Lotfußpunktes. Mit der Berechung der Länge der Strecke ist der gesuchte Abstand bestimmt.
ist der gesuchte Abstand bestimmt.
Zur Hilfe wird eine Ebene E, die orthogonal zur Geraden g ist und den Punkt P enthält aufgestellt. Der Richtungsvektor der Geraden wird dabei als Normalenvektor der Hilfsebene verwendet. Der Schnittpunkt von Gerade und Hilfsebene ist der Lotfußpunkt F. Die Länge der Strecke
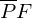 ist der gesuchte Abstand.
ist der gesuchte Abstand.Die Ebene wird beschrieben durch
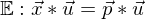 Der gemeinsame Punkt von g und
Der gemeinsame Punkt von g und 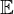 muss beide Gleichungen erfüllen, d.h. es muss gelten:
muss beide Gleichungen erfüllen, d.h. es muss gelten: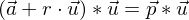
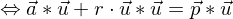
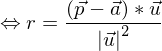
Dieser Wert für r wird in die Parameterdarstellung von g eingesetzt und man erhät die Koordinaten des Lotfußpunktes. Mit der Berechung der Länge der Strecke
 ist der gesuchte Abstand bestimmt.
ist der gesuchte Abstand bestimmt. J1: Produktions-, Entwicklungs-, und Zufallsprozesse durch Übergangsdiagramme und Matrizen beschreiben und Zustandsverktoren interpretieren.
Produktionsprozesse: Mithilfe von Matrizen lässt sich der Ablauf einer Produktion beschreiben: beispielsweise, wie sich verschiedene Produkte aus Grundelementen( also Erzeugnise aus Rohstoffen oder Enderzeugnisse aus Zwischenerzeugnissen) oder Produktionsaufträge aus einzelnen Kundenaufträgen zusammensetzen.
Entwicklungsprozesse: Man betrachtet eine Population von Individuen in verschiedenen Entwicklungsstadien, die mit gewissen Überlebenswahrscheinlichkeiten eine nächste Phase der Entwicklung erreichen, sich außerdem in bestimmten Phasen vermehren oder sterben können. In die Matrix gehen sowohl die Überlebenswahrscheinlichkeiten als auch die Reproduktionsrate als Koeffizienten ein.
Entwicklungsprozesse: Man betrachtet eine Population von Individuen in verschiedenen Entwicklungsstadien, die mit gewissen Überlebenswahrscheinlichkeiten eine nächste Phase der Entwicklung erreichen, sich außerdem in bestimmten Phasen vermehren oder sterben können. In die Matrix gehen sowohl die Überlebenswahrscheinlichkeiten als auch die Reproduktionsrate als Koeffizienten ein.
J1: Produktions-, Entwicklungs-, und Zufallsprozesse durch Übergangsdiagramme und Matrizen beschreiben und Zustandsverktoren interpretieren.
Zufallsprozesse: Die Zustände eines Systems werden mithilfe von Zustandsvektoren beschrieben. Diese geben an, mit welcher Wahrscheinlichkeit ein bestimmtes Ereigniss zu einem bestimmten Zeitpunkt eintritt. Die zugehörigen Ereignisse (Zustände) und die Wahrscheinlichkeit für die Übergänge zwischen den Ereignissen werden graphisch mithilfe eines Übergangsdiagramms beschrieben, algebraisch mithilfe der Übergangsmatrix. Dabei wird die Übergangswahrscheinlichkeit von einem Zeitpunkt E, in einen Zustand E, in die Zeile a, der Matrix eingetragen (i-te Zeile, j-te Spalte). Da die Zustandsvektoren von Zufallsprozessen eine Wahrscheinlichkeitsverteilung beschreiben, ist die Summe der Wahrscheinlichkeiten in einer Spalte der Übergangsmatrix und in jedem Zustandsvektor immer gleich eins.
J2: Zustände von Prozessen nach wiederholter Durchführung mithilfe der Matrizenmultiplikation berechnen und deuten, insbesondere bei zyklischen Prozessen.
Wird ein Prozess durch eine Matrix beschrieben, dann erhält man aus dem Ausgangsvektor durch Multiplizieren den Vektor des zeitlich nachfolgenden Zustandes und durch wiederholte Multiplikation mit der Matrix die darauf folgenden Zustände. Diese kann man direkt auch dadurch berechnen, dass man - gemäß dem Assoziativgesetz- zunächst die entsprechende Matrixpotenz berechnet und diese dann mit dem Ausgangsvektor multipliziert:
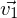 =
=  *
*  ,
, 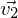 =
= 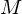 *
* 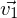 ,
, 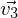 =
=  *
* 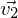 usw. oder
usw. oder 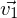 =
=  *
*  ,
,
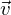 =
= ² *
² *  ,
,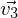 =
=  ³ *
³ *  ...
...
Gilt für irgendeine Matrixpotenz von , dass
, dass 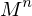 = E(Einheitsmatrix) für
= E(Einheitsmatrix) für 

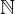 , also
, also 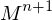 =
= , dann wird durch die Übergangsmatrix
, dann wird durch die Übergangsmatrix  ein zyklischer Prozess der Länge n beschrieben. Dies bedeutet, dass sich die Folge der Zustandsvektoren jeweils nach n Schritten wiederholt.
ein zyklischer Prozess der Länge n beschrieben. Dies bedeutet, dass sich die Folge der Zustandsvektoren jeweils nach n Schritten wiederholt.
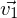 =
=  *
*  ,
, 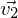 =
= 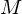 *
* 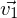 ,
, 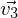 =
=  *
* 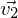 usw. oder
usw. oder 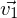 =
=  *
*  ,
,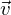 =
= ² *
² *  ,
,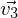 =
=  ³ *
³ *  ...
...Gilt für irgendeine Matrixpotenz von
 , dass
, dass 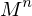 = E(Einheitsmatrix) für
= E(Einheitsmatrix) für 

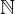 , also
, also 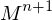 =
= , dann wird durch die Übergangsmatrix
, dann wird durch die Übergangsmatrix  ein zyklischer Prozess der Länge n beschrieben. Dies bedeutet, dass sich die Folge der Zustandsvektoren jeweils nach n Schritten wiederholt.
ein zyklischer Prozess der Länge n beschrieben. Dies bedeutet, dass sich die Folge der Zustandsvektoren jeweils nach n Schritten wiederholt.B6: Graphen auf Monotonie auf lokale und absolute Extrempunkte untersuchen und diese im Sachzusammenhang interpretieren Teil1
Monotonie:
Graph sei G von f mit f(x) und G' sei die Ableitung von f mit f'(x)
1) Wenn G'{oberhalb;unterhalb} der x-Achse verläuft, ist f streng monoton {zunehmend;abnehmend}.
2) Wenn G' die x-Achse an der Stelle xo schneidet, hat G an diese Stelle ein Extrema.
3) Wenn G' streng monoton {zunehmend;abnehmend} verläuft, hat G eine {Linkskrümmung;Rechtskrümmung}.
4) Wenn G' an der Stelle xo ein Extrema hat, so hat G an diese Stelle einen Wendepunkt.

Graph sei G von f mit f(x) und G' sei die Ableitung von f mit f'(x)
1) Wenn G'{oberhalb;unterhalb} der x-Achse verläuft, ist f streng monoton {zunehmend;abnehmend}.
2) Wenn G' die x-Achse an der Stelle xo schneidet, hat G an diese Stelle ein Extrema.
3) Wenn G' streng monoton {zunehmend;abnehmend} verläuft, hat G eine {Linkskrümmung;Rechtskrümmung}.
4) Wenn G' an der Stelle xo ein Extrema hat, so hat G an diese Stelle einen Wendepunkt.

B7: Graphenuntersuchung auf Krümmungsverhalten, Wende- und Sattelstellen
1) Krümmungsverhalten:
Wenn f''(x)>0 {f''(x)<0} gilt, dann ist der Graph von f linksgerümmt {rechtsgekrümmt}. Der Graf vom f heißt linksgekrümmt {rechtsgekrümmt } genau dann, wenn f' streng monoton steigend {fallend} ist.
2) Wendepunkte:
Notwendige Bedingung:
f''(xo)=0
Hinreichende Bedingung:
f'''(xo)>0 R/L Wendestelle
f'''(xo)<0 L/R Wendestelle
3) Sattelpunkte:
Sattelpunkte sind Wendepunkte, mit einer zur x-Achse parallelen Tangente
Wenn gilt:
f'(xo)=0
f''(xo)=0
sowie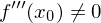 -> nur, wenn das gilt, gibt es einen Sattelpunkt.
-> nur, wenn das gilt, gibt es einen Sattelpunkt.
Wenn f''(x)>0 {f''(x)<0} gilt, dann ist der Graph von f linksgerümmt {rechtsgekrümmt}. Der Graf vom f heißt linksgekrümmt {rechtsgekrümmt } genau dann, wenn f' streng monoton steigend {fallend} ist.
2) Wendepunkte:
Notwendige Bedingung:
f''(xo)=0
Hinreichende Bedingung:
f'''(xo)>0 R/L Wendestelle
f'''(xo)<0 L/R Wendestelle
3) Sattelpunkte:
Sattelpunkte sind Wendepunkte, mit einer zur x-Achse parallelen Tangente
Wenn gilt:
f'(xo)=0
f''(xo)=0
sowie
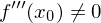 -> nur, wenn das gilt, gibt es einen Sattelpunkt.
-> nur, wenn das gilt, gibt es einen Sattelpunkt.B6: Graphen auf Monotonie auf lokale und absolute Extrempunkte untersuchen und diese im Sachzusammenhang interpretieren Teil 2
2. Lokale Extrempunkte:
Notwendige Bedingung: f'(xo)=0
Hinreichende Bedingung:
mit der 2. Ableitung, wenn f'(xo)=0 und f''(xo)>0 {f''(xo)<0}. So befindet sich an der Stelle xo ein lokales Minimum {Maximum}
Alternative hinreichende Bedingung (Vorzeichenwechselkriterium VZW):
Falls f'(xo)=0 und f' an der Stelle xo einen -/+ VZW bzw. {+/- VZW} hat, so ist an der Stelle xo ein lokales Minimum {Maximum}.
3. Absolute Extrempunkte:
Vergleicht man alle lokalen Minima {Maxima} und die Funktionwerte an den Rändern des Intervalls I, so ist der kleinste {größte} Wert daraus, das absolute Minimum {Maximum}.
Notwendige Bedingung: f'(xo)=0
Hinreichende Bedingung:
mit der 2. Ableitung, wenn f'(xo)=0 und f''(xo)>0 {f''(xo)<0}. So befindet sich an der Stelle xo ein lokales Minimum {Maximum}
Alternative hinreichende Bedingung (Vorzeichenwechselkriterium VZW):
Falls f'(xo)=0 und f' an der Stelle xo einen -/+ VZW bzw. {+/- VZW} hat, so ist an der Stelle xo ein lokales Minimum {Maximum}.
3. Absolute Extrempunkte:
Vergleicht man alle lokalen Minima {Maxima} und die Funktionwerte an den Rändern des Intervalls I, so ist der kleinste {größte} Wert daraus, das absolute Minimum {Maximum}.
Flashcard set info:
Author: Exinator
Main topic: Mathematik
Topic: Abiturvorbereitung
School / Univ.: MGS
City: Schwelm
Published: 28.03.2011
Card tags:
All cards (26)
no tags



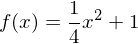 begrenzt mit den y-Achse und der Geraden mit der Gleichung
begrenzt mit den y-Achse und der Geraden mit der Gleichung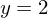 und
und 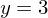 eine Fläche. Bestimmen Sie das Volumen.
eine Fläche. Bestimmen Sie das Volumen.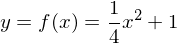 folgt
folgt 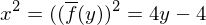 . Nach der Regel für das Volumen folgt:
. Nach der Regel für das Volumen folgt: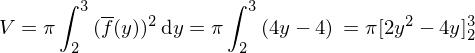
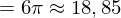
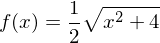 begrenzt mit den Koordinatenachsen und der Geraden mit der Gleichung
begrenzt mit den Koordinatenachsen und der Geraden mit der Gleichung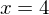 eine Fläche. Bestimmen Sie das Volumen.
eine Fläche. Bestimmen Sie das Volumen.