Warum hat eine ganzrationale Funktion vom Grad n höchstens n Nullstellen?
Jede Nullstelle 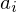 einer ganzrationalen Funktion erzeugt in der Produktform einen Linearfaktor der Form
einer ganzrationalen Funktion erzeugt in der Produktform einen Linearfaktor der Form 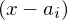 .
.
Gäbe es mehr als n Nullstellen, könnte man die Funktion in der Produktdarstellung mit mehr als n Linearfaktoren darstellen. Beim Ausmultiplizieren wäre hierbei die größte x-Potenz größer als n. Das kann nicht sein.
Beachte: Es gibt natürlich ganzrationale Funktionen vom Grad n mit weniger als n Nullstellen.
Beispiel: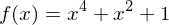 hat gar keine Nullstelle.
hat gar keine Nullstelle.
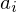 einer ganzrationalen Funktion erzeugt in der Produktform einen Linearfaktor der Form
einer ganzrationalen Funktion erzeugt in der Produktform einen Linearfaktor der Form 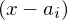 .
. Gäbe es mehr als n Nullstellen, könnte man die Funktion in der Produktdarstellung mit mehr als n Linearfaktoren darstellen. Beim Ausmultiplizieren wäre hierbei die größte x-Potenz größer als n. Das kann nicht sein.
Beachte: Es gibt natürlich ganzrationale Funktionen vom Grad n mit weniger als n Nullstellen.
Beispiel:
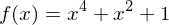 hat gar keine Nullstelle.
hat gar keine Nullstelle.Tags: ganzrational, Grad, Nullstelle
Quelle:
Quelle:
Kartensatzinfo:
Autor: www.mathematik-bw.de
Oberthema: Mathematik
Thema: 10. Klasse
Schule / Uni: Clara-Schumann-Gymnasium
Ort: Lahr
Veröffentlicht: 23.12.2009
Schlagwörter Karten:
Alle Karten (47)
Ableitung (10)
Änderungsrate (9)
Anwendung (2)
Begriffe (17)
Definitionsmenge (1)
Extremstelle (2)
Funktion (8)
ganzrational (5)
Gerade (13)
Grad (1)
h-Methode (6)
hinreichend (3)
Intervalle (1)
Normale (2)
notwendig (2)
Nullstelle (5)
Produktform (3)
Sattelpunkt (3)
Schnittwinkel (1)
Sekante (1)
Sekantensteigung (1)
Steigungswinkel (3)
Streckung (1)
Symmetrie (3)
Tangente (7)
Terassenpunkt (3)
Verschiebung (7)
Wertemenge (1)



