Eigenschaften von Szenegraphen? Konkrete Softwarenamen?
baumartige Hierarchie (meistens Gruppen-, Transformation- und Geometrieknoten)
Wissen wo man sich in der Welt befindet.
Änderungen von Knoten wirkt sich auf Kinder aus.
Zustand wird sich gemerkt (z.B. Transformation). Beim Verlassen eines Teilbaums wird dieser wieder restauriert (äquivalent zu glPush/PopMatrix()).
OpenSG, JME, Ogre3D, Open Inventor, ....
Wissen wo man sich in der Welt befindet.
Änderungen von Knoten wirkt sich auf Kinder aus.
Zustand wird sich gemerkt (z.B. Transformation). Beim Verlassen eines Teilbaums wird dieser wieder restauriert (äquivalent zu glPush/PopMatrix()).
OpenSG, JME, Ogre3D, Open Inventor, ....
Szenegraph wurde vorgegeben. Wie berechne ich die Weltkoordinaten für die Positionierung der Objekte/BBs ? Wie aus Welt- lokale Koordinaten?
Von lokal in Welt Matrizen aufmultiplizieren von links. Andersrum die Inversen der Matrizen.
Also geg. z.B. Root -> M1 -> M3 -> M2 -> Geometrie
Dann lokal -> Welt: M1*M3*M2*pl = pw
Welt -> lokal: pl = M2^-1*M3^-1*M1^-1*pw
= (M1*M3*M2)^-1*pw
Also geg. z.B. Root -> M1 -> M3 -> M2 -> Geometrie
Dann lokal -> Welt: M1*M3*M2*pl = pw
Welt -> lokal: pl = M2^-1*M3^-1*M1^-1*pw
= (M1*M3*M2)^-1*pw
Wie bekommt man die View-Matrix (gluLookAt-Matrix)?
View-Matrix macht die Umformung von Welt- in Kamerakoordinaten.
Hier also Aufmultiplizieren der Inversen der Matrizen von links.
Die Modelviewmatrix berechnet sich aus der Akkumulation der Transformationsmatrizen(z.B.: R*S*...*T) und der “gluLookAt-Matrix”(V). (Mv= V R S ... T), wobei für V alle Transformationen im SG zwischen ihr und dem Root-Knoten erst akkumuliert und dann invertiert mit ihr multipliziert werden müssen: VW = (R S ... T)-1 VL = T-1 ... S-1 R-1 VL.
Hier also Aufmultiplizieren der Inversen der Matrizen von links.
Die Modelviewmatrix berechnet sich aus der Akkumulation der Transformationsmatrizen(z.B.: R*S*...*T) und der “gluLookAt-Matrix”(V). (Mv= V R S ... T), wobei für V alle Transformationen im SG zwischen ihr und dem Root-Knoten erst akkumuliert und dann invertiert mit ihr multipliziert werden müssen: VW = (R S ... T)-1 VL = T-1 ... S-1 R-1 VL.
(-t)*R*p ist äquivalent zu ?
a) R(p-t)
b) R*p-t
R(p-t) ist äquivalent zu ?
a) R*T*p
b) T*R*P
a) R(p-t)
b) R*p-t
R(p-t) ist äquivalent zu ?
a) R*T*p
b) T*R*P
1)Zuerst wird rotierte und danach transliert, also b)
(einfache Arithmetik, nicht verunsichern lassen)
2)Erst wird transliert, dann rotiert, also a)
Wenn p -> 4D-Vektor und R und T 4x4-Matrizen dann liefert a) das selbe Ergebnis.
(einfache Arithmetik, nicht verunsichern lassen)
2)Erst wird transliert, dann rotiert, also a)
Wenn p -> 4D-Vektor und R und T 4x4-Matrizen dann liefert a) das selbe Ergebnis.
Wo ist die Kamera?
Hängt davon ab, ob Szene statisch oder dynamisch
statische Szene: direkt unter Wurzel
dynamische Szene: unter den Geometrieknoten des bewegten Objekts
Mittransformieren der Kamera
Bsp: So positionieren dass sie am Kopf einer Figur sitzt. Die Transformationen des Kopfes wirken sich so auch auf die Kamera aus.(First Person View).
statische Szene: direkt unter Wurzel
dynamische Szene: unter den Geometrieknoten des bewegten Objekts
Mittransformieren der Kamera
Bsp: So positionieren dass sie am Kopf einer Figur sitzt. Die Transformationen des Kopfes wirken sich so auch auf die Kamera aus.(First Person View).
Wo ist die Lichtquelle?
Auch beliebig. Kann bspw. an einen Geometrieknoten gehangen werden, wenn sie sich bewegen soll.(Taschenlampe)
Lichtquellen werden genau wie andere Objekte innerhalb der Szene platziert. (Licht Position wird von OpenGL genauso behandelt wie die eines Vertex ). Während das beim AmbientLight nicht unbedingt nötig wäre, profitieren gerichtete Lichtquellen und punktförmige Lichtquellen von der Objektgruppierung.
Lichtquellen werden genau wie andere Objekte innerhalb der Szene platziert. (Licht Position wird von OpenGL genauso behandelt wie die eines Vertex ). Während das beim AmbientLight nicht unbedingt nötig wäre, profitieren gerichtete Lichtquellen und punktförmige Lichtquellen von der Objektgruppierung.
Sortieren bei Szenegraphen, wann braucht man das?
Zur Optimierung. (Draw Tree): z.B. Geometrie mehrfach referenzieren(1x im Speicher), Minimierung der State Changes (nach Textur(am teuersten!),Materialien,Farbe,Shader sortieren)
Man will verhindern dass die Pipeline “leerläuft” (viele State Changes -> “Langsamster Renderer der Welt”)
Sortieren nach Transparenzen. Transparenzen als letztes zeichnen.
Man will verhindern dass die Pipeline “leerläuft” (viele State Changes -> “Langsamster Renderer der Welt”)
Sortieren nach Transparenzen. Transparenzen als letztes zeichnen.
Wenn die Kamera weiter unten ist, muss ich dann für weiter oben liegende Geometrie quasi zweimal durch den Graph?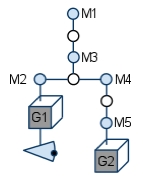

Ja, einmal um die View-Matrix zu akkumulieren. Anschließend wird die Geometrie der Szene mit dieser View gezeichnet.
Bsp.: Cockpitsicht. View Matrix an Geometrie G1 (im Auto). Zur Berechnung der View Matrix: V = M2-1 * M3-1 * M1-1 . Danach Geometrie mit View-Matrix zeichnen: G1w = V * M1 * M2 * M3 * G1l
Bsp.: Cockpitsicht. View Matrix an Geometrie G1 (im Auto). Zur Berechnung der View Matrix: V = M2-1 * M3-1 * M1-1 . Danach Geometrie mit View-Matrix zeichnen: G1w = V * M1 * M2 * M3 * G1l
Wofür braucht man die Boundingboxen? Welche gibt es?
View-Frustum-Culling:
Wenn BV außerhalb des Frustums liegt, braucht der darunter liegende Graph für das Rendering nicht weiter berücksichtigt werden. Jedem Objekt wird ein BV zugeordnet, Mehrfachrendern von Geomtrie ist somit nicht möglich.
AABB, Oriented BB, Bounding Slaps (k-dops), Kugel
Wenn BV außerhalb des Frustums liegt, braucht der darunter liegende Graph für das Rendering nicht weiter berücksichtigt werden. Jedem Objekt wird ein BV zugeordnet, Mehrfachrendern von Geomtrie ist somit nicht möglich.
AABB, Oriented BB, Bounding Slaps (k-dops), Kugel
Wie funktioniert VFC?
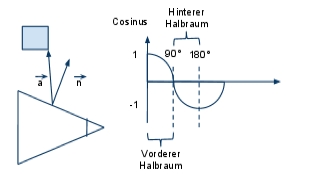 Von oben nach unten testen ob Geometrie im Frustum liegt.
Von oben nach unten testen ob Geometrie im Frustum liegt.Konkret:
Man testet die 8 Eckpunkte des Bounding Volumes (hier Bounding Box) gegen jede Ebene des View-Frustums.
dot(n:Normale der Ebene, a:EckpunktBV-Punkt auf Ebene) > 0: Punkt im vorderen Halbraum (dahin wo die Normale zeigt, also außerhalb)
sonst: hinteren Halbraum (innerhalb)
Hier: Normalen der Ebenen des Frustums zeigen nach außen
1. BV komplett vor mindestens einer Ebene (Eckpunkte: dot(a,n) > 0 ) -> Objekt nicht sichtbar, Abbruch
2. BV hinter allen 6 Ebenen -> Objekt komplett sichtbar, alle enthaltene Geometrie zeichnen.
3. BV mindestens durch eine Ebene teilweise abgeschnitten -> weder davor noch dahinter :wenn Gruppenknoten -> weiter absteigen
wenn Geometrie -> zeichnet man einfach alles
Welche Eigenschaften haben B-Splines (basisfunktionen)?
Die Summe aller Gewichtungsfunktionen (Ergebnisse der jeweiligen Cox de Boor-Rekursion) ergibt in der Regel 1, bis auf (k − 1) Intervalle am Anfang und Ende.
Die Gewichtungsfunktionen werden NIE negativ
Maximale Ordnung der B-Splines ist k = n.
Jeder Kontrollpunkt auf der Kurve wird durch k Nachbarpunkte beeinflusst
Die B-Spline Kurve liegt in der Vereinigung aller konvexer Hu ̈llen um jeweils k aufeinanderfolgende Kontrollpunkte.
Invariant bezu ̈glich affiner Abbildungen (egal ob erst abbilden, dann berechnen oder andersrum) projektiv allerdings NICHT invariant
Die Gewichtungsfunktionen werden NIE negativ
Maximale Ordnung der B-Splines ist k = n.
Jeder Kontrollpunkt auf der Kurve wird durch k Nachbarpunkte beeinflusst
Die B-Spline Kurve liegt in der Vereinigung aller konvexer Hu ̈llen um jeweils k aufeinanderfolgende Kontrollpunkte.
Invariant bezu ̈glich affiner Abbildungen (egal ob erst abbilden, dann berechnen oder andersrum) projektiv allerdings NICHT invariant
Welche Arten von B-Splines gibt es und was sind ihre Eigenschaften?
Es gibt periodische und offene B-Splines. In der Regel sind diese noch uniform, d.h. die Werte im Knotenvektor haben gleiche Absta ̈nde.
periodisch uniforme B-Splines
Abstand zwischen den Knotenwerten ist konstant (z.B. [0, 1, 2, ..]) Ein Punkt der Kurve liegt immer in der konvexen Hu ̈lle der k Nachbarpunkte, die ihn beeinflussen Der komplette Spline liegt damit in der Vereinigung dieser konvexen Hu ̈llen Spitze in der Kurve wird erzeugt durch k − 1 identische aufeinanderfolgende Kontrollpunkte Geschlossene Kurve: Wiederholung von k − 2 Kontrollpunkten Die Kurve ist gu ̈ltig im Intervall fu ̈r Parameter t [k − 1, n]
offen uniforme B-Splines
An Anfang und Ende des Knotenvektors stehen je k gleiche Werte, z.B. [0..0123..3] Kurve geht durch ersten und letzten Kontrollpunkt
Fu ̈r n = k ergibt sich dann eine Bezier-Kurve (Knotenvektor [0..01..1]). Vorteil gegenu ̈ber Bezier-Splines ist die lokale Kontrolle, d.h. die Kontrollpunkte vera ̈ndern die Kurve nur lokal.
Die Kurve ist gu ̈ltig im Intervall fu ̈r Parameter t [0, n − k + 1].
periodisch uniforme B-Splines
Abstand zwischen den Knotenwerten ist konstant (z.B. [0, 1, 2, ..]) Ein Punkt der Kurve liegt immer in der konvexen Hu ̈lle der k Nachbarpunkte, die ihn beeinflussen Der komplette Spline liegt damit in der Vereinigung dieser konvexen Hu ̈llen Spitze in der Kurve wird erzeugt durch k − 1 identische aufeinanderfolgende Kontrollpunkte Geschlossene Kurve: Wiederholung von k − 2 Kontrollpunkten Die Kurve ist gu ̈ltig im Intervall fu ̈r Parameter t [k − 1, n]
offen uniforme B-Splines
An Anfang und Ende des Knotenvektors stehen je k gleiche Werte, z.B. [0..0123..3] Kurve geht durch ersten und letzten Kontrollpunkt
Fu ̈r n = k ergibt sich dann eine Bezier-Kurve (Knotenvektor [0..01..1]). Vorteil gegenu ̈ber Bezier-Splines ist die lokale Kontrolle, d.h. die Kontrollpunkte vera ̈ndern die Kurve nur lokal.
Die Kurve ist gu ̈ltig im Intervall fu ̈r Parameter t [0, n − k + 1].
Welche Arten der Stetigkeit gibt es? Welche Effekte hat das auf die Beleuchtung?
C0: Positions-Stetigkeit. Polynome treffen aufeinander, sonst keine Bedingung. Effekt: Störungen bei Lichteffekten
C1: Tangentiale Stetigkeit: Tangenten der Polynome im Treffpunkt sind identisch. Effekt: Ausreichend gute Beleuchtung
C2: Krümmungsstetigkeit: Betrag der Tangenten auch gleich. Optisch perfekt glatt
C0-C1=G0-G1
G2: Parametrisierung auch stetig
C1: Tangentiale Stetigkeit: Tangenten der Polynome im Treffpunkt sind identisch. Effekt: Ausreichend gute Beleuchtung
C2: Krümmungsstetigkeit: Betrag der Tangenten auch gleich. Optisch perfekt glatt
C0-C1=G0-G1
G2: Parametrisierung auch stetig
B-Splines: Erklären:
Bi, n, k, xi, t
Bi, n, k, xi, t
Bi: Cox-deBoor Punkt, zwischen denen interpoliert wird
n: Anzahl der Kontrollpunkte und Basisfunktionen
k: Ordnung des Polynoms (Anzahl der Kontrollpunkte, die einen Kurvenabschnitt beeinflussen),
k-1 Grad der Polynome,
k-2 Stetigkeit
xi: Element des Knotenvektors, Intervallgrenzen
t: Parameter entlang der B-Spline-Kurve
n: Anzahl der Kontrollpunkte und Basisfunktionen
k: Ordnung des Polynoms (Anzahl der Kontrollpunkte, die einen Kurvenabschnitt beeinflussen),
k-1 Grad der Polynome,
k-2 Stetigkeit
xi: Element des Knotenvektors, Intervallgrenzen
t: Parameter entlang der B-Spline-Kurve
Was sind Knotenvektoren?
Knotenvektoren sind monoton steigende Zahlenfolgen mit n+k Eintra ̈gen, z.B. [000. . . 111], [0123] im uniformen Fall (nicht uniform [0 2 5]). Durch die Angabe von Knotenvektoren werden die Basisfunktionen festgelegt. Die Elemente haben einen Index, beginnend bei 1.
Was kann man damit machen? (offen, periodischer B-Spline)
Schöne Kurven. Hübsch gebogen und geformt. Kann man anschauen und bestaunen.
^^schlechte Antwort!, vielleicht besser:
period. B-Spline, der geschlossen ist: Trimmingkurve
offener B-Spline: Kurve, die durch STart und Ende geht, dafür nicht schön zu schliessen
^^schlechte Antwort!, vielleicht besser:
period. B-Spline, der geschlossen ist: Trimmingkurve
offener B-Spline: Kurve, die durch STart und Ende geht, dafür nicht schön zu schliessen
Wie zeichne ich eine Freiformfläche?
Doppelter de Casteljau:
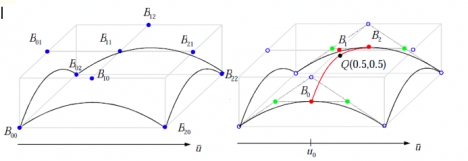
Um den Punkt Q(0.5, 0.5) auf der Bezierfläche zu berechnen, müssen als erstes B0, B1, B2 berechnet werden. Um B0 zu berechnen wird der normale de Casteljau Algorithmus für Bezier-Kurven angewandt, d.h. zwischen den Punkten B00 und B10 wird mit u0= 0.5linear interpoliert, genauso wie zwischen B10 und B20. Man erhält so die beiden vordersten grünen Punkte. Interpoliert man nun erneut zwischen diesen beiden neuberechneten Punkten erhält man B0. Analog werden B1und B2berechnet.
Auf B0, B1, B2 wird ebenfalls der de Casteljau-Algorithmus angewandt, allerdings mit v0=0.5. Der nun berechnete Punkt ist Q(0.5, 0.5) und liegt auf der Bezierfläche.

Um den Punkt Q(0.5, 0.5) auf der Bezierfläche zu berechnen, müssen als erstes B0, B1, B2 berechnet werden. Um B0 zu berechnen wird der normale de Casteljau Algorithmus für Bezier-Kurven angewandt, d.h. zwischen den Punkten B00 und B10 wird mit u0= 0.5linear interpoliert, genauso wie zwischen B10 und B20. Man erhält so die beiden vordersten grünen Punkte. Interpoliert man nun erneut zwischen diesen beiden neuberechneten Punkten erhält man B0. Analog werden B1und B2berechnet.
Auf B0, B1, B2 wird ebenfalls der de Casteljau-Algorithmus angewandt, allerdings mit v0=0.5. Der nun berechnete Punkt ist Q(0.5, 0.5) und liegt auf der Bezierfläche.
Eigenschaften von Bezier-Freiformflächen?
Grad der Flächen in jede Parameterrichtung ist eins wenigerals die Anzahl der Kontrollpunkte in diese Richtung
Stetigkeit ist zwei weniger
Die Eckpunkte des Kontrollnetzes liegen auf der Bézier-Fläche
Die Fläche liegt in der konvexen Hülle des Kontrollnetzes
Affine Invarianz
Stetigkeit ist zwei weniger
Die Eckpunkte des Kontrollnetzes liegen auf der Bézier-Fläche
Die Fläche liegt in der konvexen Hülle des Kontrollnetzes
Affine Invarianz
Wie findet man heraus ob man verfeinern muss?
1)Freiformfläche mit Hilfe des Kontrollnetzes in Vierecke unterteilen
2)Für jedes Viereck überprüfen, ob die Abweichung von der Fläche größer als ein vorgegebenes € ist, falls ja: weitere Unterteilung des Vierecks unter Verwendung weiterer Punkte der Freiformfläche (die in diesem Rechteck liegen)
3)Funktion rekursiv fortsetzen, bis die Abweichung für jedes Viereck kleiner ist als € (Surface-Subdivision-Algorithmus)
4)Jedes Viereck triangulieren (trivial)
oder:
Große Differenzen zwischen Tangente sowie Krümmung (bzw. Normale) von benachbarten Punkten können weiteren Aufschluss darüber liefern, ob verfeinert werden muss. Zitat Müller: “Abhängig vom Gradienten der Fläche bzw. der Tangenten wählt man kleinere Flächen.” (Die Tangenten kann man durch die Partielle Ableitung nach u und v für jeden Punkt bestimmen.)
2)Für jedes Viereck überprüfen, ob die Abweichung von der Fläche größer als ein vorgegebenes € ist, falls ja: weitere Unterteilung des Vierecks unter Verwendung weiterer Punkte der Freiformfläche (die in diesem Rechteck liegen)
3)Funktion rekursiv fortsetzen, bis die Abweichung für jedes Viereck kleiner ist als € (Surface-Subdivision-Algorithmus)
4)Jedes Viereck triangulieren (trivial)
oder:
Große Differenzen zwischen Tangente sowie Krümmung (bzw. Normale) von benachbarten Punkten können weiteren Aufschluss darüber liefern, ob verfeinert werden muss. Zitat Müller: “Abhängig vom Gradienten der Fläche bzw. der Tangenten wählt man kleinere Flächen.” (Die Tangenten kann man durch die Partielle Ableitung nach u und v für jeden Punkt bestimmen.)
Herr Müller hat dann eine Kurve gemalt und zwei Punkte darauf, an denen die Normale gleich war, dazwischen war aber eine Beule in der Kurve. Die Kurve war unter den zwei Punkten auch gekrümmt. Was macht man da? Funktioniert das immer?
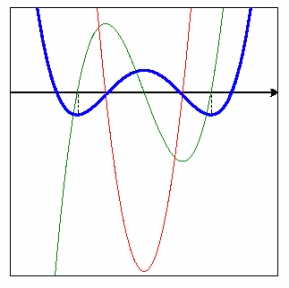
Kann man sich ja die Krümmung (2. Ableitung) berechnen, wenn die hoch ist: verfeinern.
Funktioniert das denn immer?
Nein, wenn die Fläche links und rechts, da wo man seine beiden Punkte ausgerechnet hat, ganz flach ist und dazwischen ist einer Beule in der Kurve, dann würde man die auch verpassen. Herr Müller meinte darauf, stimmt, es gibt scheinbar kein Verfahren bei dem man sich sicher sein kann. Mit dem oben beschriebenen Verfahren würde man auch eine solche “Beule” finden und verfeinern
Aber findet die Verfeinerung nicht automatisch statt? (Malt mir eine durch Bézier dargestellte Kurve auf, die dort, wo die Krümmung am höchsten ist auch die meisten Punkte anhäuft) Wie kriege ich die Krümmung der Fläche an einer Stelle?
Zweite Ableitung, die erste Ableitung (Tangente) kriege ich bei DeCasteljau ohnehin schon; haben dann länger gemeinsam überlegt, ob es nicht möglich wäre daraus einfach die Krümmung zu bekommen, ohne Aufwendiges Ableiten etc.)
Wie funktioniert die Newton-Iteration?
Strahl- und Oberflächengleichung gleichsetzen => nichtlineares Nullstellenproblem
Mit der N-I kann dieses angenähert werden:
Sehstrahl = Koordinatenachse x
Startpunkt -> Punkt x1 in Nähe des gesuchten Nullpunkts: Approximierung durch viele kleine Bounding Volumes um Fläche. Strahl mit diesen schneiden um x1 zu bestimmen.
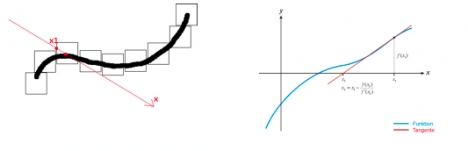
Man berechnet an der Stelle x1 jetzt die Tangente, da wo die Tangente die x-Achse schneidet, berechnet man den Funtionswert und hat einen neuen Schätzwert x2. Iteration bis die Funktion an der Stelle einen sehr kleinen Wert annimmt, sich der Schätzwert nicht mehr groß ändert, oder ein Maximum an n Iterationen überschritten wurde.
Möglichst eng anliegende, kleine BVs um Teile der Fläche bilden um gute Startwerte für das iterative Verfahren zu haben, wird sonst unperformant oder konvergiert nicht.
Macht man allerdings zu viele kleine BVs wird der Aufwand für die Schnitttests mit den BVs unverhältnismäßig hoch. Das richtige Verhältnis zwischen Aufwand für Newton Iteration und die BV Schnitttests muss man also abwägen.
Mit der N-I kann dieses angenähert werden:
Sehstrahl = Koordinatenachse x
Startpunkt -> Punkt x1 in Nähe des gesuchten Nullpunkts: Approximierung durch viele kleine Bounding Volumes um Fläche. Strahl mit diesen schneiden um x1 zu bestimmen.
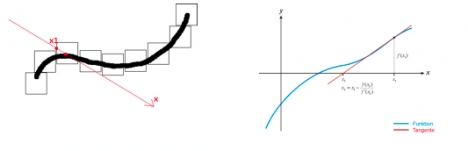
Man berechnet an der Stelle x1 jetzt die Tangente, da wo die Tangente die x-Achse schneidet, berechnet man den Funtionswert und hat einen neuen Schätzwert x2. Iteration bis die Funktion an der Stelle einen sehr kleinen Wert annimmt, sich der Schätzwert nicht mehr groß ändert, oder ein Maximum an n Iterationen überschritten wurde.
Möglichst eng anliegende, kleine BVs um Teile der Fläche bilden um gute Startwerte für das iterative Verfahren zu haben, wird sonst unperformant oder konvergiert nicht.
Macht man allerdings zu viele kleine BVs wird der Aufwand für die Schnitttests mit den BVs unverhältnismäßig hoch. Das richtige Verhältnis zwischen Aufwand für Newton Iteration und die BV Schnitttests muss man also abwägen.
Wie erhalte ich die Texturpositionen auf der Ebene?
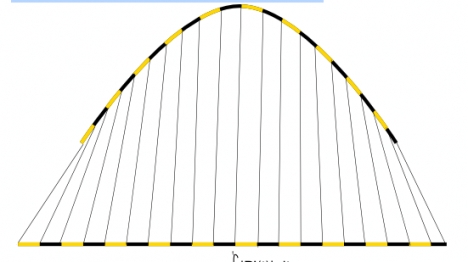
Damit jeder Texel auf einer Kurve ein gleichlanges Kurvensegment texturiert, muss man mit s(t) = auP’(t) die zurückgelegte Strecke auf der Kurve berechnen. Dieser Weg muss für die Texturierung nur auf den Wertebereich von 0 bis 1 skaliert werden, d.h. eine Division durch die Gesamtstrecke. Im Fall der Bezierkurven ist der gültige Wertebereich für t, das Intervall von 0 bis 1. Eine sinnvolle eindimensionale Texturkoordinate einer Bezierkurve wäre also:
sTexture(t) =0tP’(t) dt 01P’(t)dt mit 0t1
Für eine Bezierfläche könnte man dieses Verfahren auch in u und v Richtung anwenden.
Integral leider nicht trivial lösbar. Alternativ könnte man die Kurve Triangulieren. Die einfach zu berechnenden Strecken zwischen den Punkten nähern das Integral dann abhängig vom Feinheitsgrad der Triangulierung effizient an.
Der naive Ansatz wäre u und v direkt als Texturkoordinaten verwenden.
Welche Eigenschaften haben Trimm-Kurven?
Parameterbereich der Flächen wird zusätzlich durch Trimm-Kurven eingeschränkt (z.B. Löcher)
geschlossen
dürfen sich nicht schneiden
konsistent orientiert, d.h. wenn ri der Vater von rj ist, dann haben beide auch unterschiedlichen Umlaufsinn. So kann innnen und außen unterschieden werden.
OpenGL unterstützt getrimmte NURBS-Patches.
geschlossen
dürfen sich nicht schneiden
konsistent orientiert, d.h. wenn ri der Vater von rj ist, dann haben beide auch unterschiedlichen Umlaufsinn. So kann innnen und außen unterschieden werden.
OpenGL unterstützt getrimmte NURBS-Patches.
Wenn ich eine Freiformfläche habe und in der Mitte eine Trimming-Kurve, wie teste ich dann ob ein Punkt in der Kurve liegt?
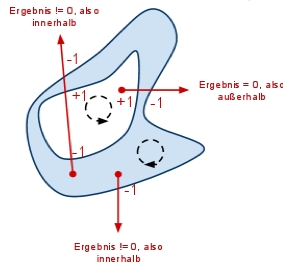 Strahl in irgendeine Richtung vom Punkt wegschicken. Umgekehrter Umlaufsinn
Strahl in irgendeine Richtung vom Punkt wegschicken. Umgekehrter Umlaufsinnder Kurven. Zähler hoch/runter zählen bei Ein-/Austritt aus Kurven. Wert des Zählers am Ende sagt aus, ob inner- oder ausserhalb der Kurve.
Wie kann man innerhalb eines getrimmten, ungültigen Bereichs wiederum
einen gültigen Bereich haben?
einen gültigen Bereich haben?
Das zielt auf den eindeutigen Umlaufsinn der Trimmkurven ab. Liegt ein solcher vor, kann anhand der Schnitte eines Strahls mit den Trimmkurven entschieden werden, ob ein Parameterwert-Paar (u, v) gültig ist.
Was ist die Aufgabe des Vertexshaders? Was nicht? Auf welchen Daten arbeitet er?
Arbeitet nur auf Eckpunktdaten: Eckpunkttransformation(Welt->Kamerakoord., Transformation ins kanonische Volumen), Normalentransformation, Beleuchtung in Kamerakoordianten, ...
Was nicht?
Clipping am kanonischen Volumen(-w..+w), perspektivische Division, Color Clamping, ...
Was nicht?
Clipping am kanonischen Volumen(-w..+w), perspektivische Division, Color Clamping, ...
Was sind uniform/varying Parameter? (Shader)
Varying Variablen sind Variablen, deren Wert im Vertexshader pro Eckpunkt berechnet wird. Aus diesen Werten wird im Fragmentshader für jeden Pixel jeweils ein interpolierter Wert berechnet (zB. Farbe, Normale, Position und Texturkoordinaten).
Mit Uniform Variablen, können Daten, die sich vergleichsweise selten ändern(konstanter Wert für Primitiv), zwischen Applikation und Shader ausgetauscht werden.Benutzerdefinierte Daten können so in den Shader geladen werden. Über Built-in Uniforms kann auch auf OpenGL States zugegriffen werden (zB. Modelviewmatrix, Projektionsmatrix, Texturmatrix, Licht-States), diese werden automatisch gesetzt. Innerhalb der Shader besteht nur Lesezugriff.
Mit Uniform Variablen, können Daten, die sich vergleichsweise selten ändern(konstanter Wert für Primitiv), zwischen Applikation und Shader ausgetauscht werden.Benutzerdefinierte Daten können so in den Shader geladen werden. Über Built-in Uniforms kann auch auf OpenGL States zugegriffen werden (zB. Modelviewmatrix, Projektionsmatrix, Texturmatrix, Licht-States), diese werden automatisch gesetzt. Innerhalb der Shader besteht nur Lesezugriff.
Wie funktioniert das Shadowmapping?
Idee:
1. Kamera in Lichtquelle setzen (Spotlight)
2. Z-Buffer von Lichtquelle aus in Textur kopieren -> Shadow Map
3. Projektives Texturmapping mit Shadow Map:
- "Nachbau" der OpenGL-Pipeline aus Sicht der Lichtquelle und Ablegen in der Textur-Matrix
- Projektive Texturkoordinaten = Transformation der Texturkoordinaten jedes Eckpunkts mit dieser Textur-Matrix
4. Pro Pixel Z Wert in Textur an (s/q, t/q) mit Z Wert in Licht Koordinatensystem (r/q) vergleichen
1. Kamera in Lichtquelle setzen (Spotlight)
2. Z-Buffer von Lichtquelle aus in Textur kopieren -> Shadow Map
3. Projektives Texturmapping mit Shadow Map:
- "Nachbau" der OpenGL-Pipeline aus Sicht der Lichtquelle und Ablegen in der Textur-Matrix
- Projektive Texturkoordinaten = Transformation der Texturkoordinaten jedes Eckpunkts mit dieser Textur-Matrix
4. Pro Pixel Z Wert in Textur an (s/q, t/q) mit Z Wert in Licht Koordinatensystem (r/q) vergleichen
Was steht im Vektor (s,t,r,q)T drin?
s/q t/q liefern mir die Texturkoordinaten, an denen man den minimalen Tiefenwert aus der Shadow Map ablesen kann. r/q ist die Tiefe des zu untersuchenden Fragments aus Sicht der Lichtquelle. Vergleich von r/q mit dem Tiefenwert an der Stelle s/q t/q in der Shadow Map sagt aus, ob das Fragment im Schatten liegt oder nicht.
Was ist denn ein Problem von Shadow Mapping?
Aliasing bei der Schattenberechnung. Effekt größer wenn Lichtquelle weiter entfernt: 1 Pixel der Shadowmap deckt mehrere Pixel im Framebuffer ab.
Lösungsmöglichkeiten:
höhere Auflösung der SM
PCF: Tiefenvergleich mit Nachbar-Texeln aus der SM und Interpolation
post-perspective SMs
ShadowMap mehrmals aus leicht unterschiedlichen Positionen rendern und zu einer Akkumulieren
Selbstverdeckung (Schatten auf Oberflächen, wo kein Schatten sein soll)
Polygonoffset
Front face culling
Auflösung der ShadowMap erhöhen
Clamping von ungültigen Werten in der Shadowmap
Nur Spotlights
Z-Fighting
Lösungsmöglichkeiten:
höhere Auflösung der SM
PCF: Tiefenvergleich mit Nachbar-Texeln aus der SM und Interpolation
post-perspective SMs
ShadowMap mehrmals aus leicht unterschiedlichen Positionen rendern und zu einer Akkumulieren
Selbstverdeckung (Schatten auf Oberflächen, wo kein Schatten sein soll)
Polygonoffset
Front face culling
Auflösung der ShadowMap erhöhen
Clamping von ungültigen Werten in der Shadowmap
Nur Spotlights
Z-Fighting
Könnten wir beim Shadow Mapping statt der Tiefe der vordersten auch die Tiefe der hintersten Punkte der Objekte abspeichern (Backfaces)?
Ja, das funktioniert mittels Frontface-Culling bevor aus Sicht der Lichtquelle gerendert wird. Danach muss das Culling wieder deaktiviert werden. Selbstverdeckung wird minimiert ohne Polygonoffset.
Könnten wir auch die Tiefe von Punkten die mitten im Objekt liegen in der Shadow Map abspeichern?
Bin darauf gekommen dass auch dies funktionieren würde, da man für im Schatten liegenden Objekte im Vergleich immer noch größere Tiefenwerte erhielte und somit korrekt schattieren würde. Dann erläuterte Prof. Müller mir den Hintergrund dieser zwei etwas eigenartigen Fragen:
Wenn man zwei Shadow Maps, einmal von den Vorder-, dann von den Rückseiten der Objekte erstellt und dann diese Tiefenwerte mittelt bekommt man Durchschnittswerte die sich auf einer Z-Achse mit viel geringerer Tiefenauflösung abspeichern lassen, was Speicherplatz spart (bzw. kann man dafür im Gegenzug die räumliche Auflösung der Shadow Map erhöhen, was das Aliasing Problem reduziert).
Triangulieren Sie nach Delauny und nennen Sie die Eigenschaften.
Anzahl der Triangulierungen einer endlichen Punktmenge S ist endlich, d.h. es gibt eine optimale Triangulierung, die den minimalen Winkel maximiert.
Analoge Definition: für jedes Dreieck ist kein weiterer Punkt im Umkreis des Dreiecks. Aber es kann mehrere dieser Lösungen geben.
Ein Problem der Delaunay Triangulierung ist, daß als Resultat immer die konvexe Hülle entsteht. Daher braucht man Algorithmen, die nachträglich die Kanten entfernen, die „man nicht haben will“.
Analoge Definition: für jedes Dreieck ist kein weiterer Punkt im Umkreis des Dreiecks. Aber es kann mehrere dieser Lösungen geben.
Ein Problem der Delaunay Triangulierung ist, daß als Resultat immer die konvexe Hülle entsteht. Daher braucht man Algorithmen, die nachträglich die Kanten entfernen, die „man nicht haben will“.
Algorithmus der Delauny Triangulierung:
Suche einen Punkt am Rand (z.B.x-Koordinate). Suche nächstgelegenen Punkt(kürzester Abstand). Schleife über alle Punkte. Berechne Winkel im Dreieck am neuen Punkt Wähle Dreieck mit max. Winkel Rekursion über 2 neue Kanten Schleife über alle Punkte im vorderen Halbraum Berechne Winkel im Dreieck am neuen Punkt Wähle Dreieck mit max. Winkel.
Triangulierung in 3D:
Mit Delaunay, allerdings mit Tetraedern Minimaler Winkel in der Tetraeder-Spitze maximieren (Raumwinkel) Problem: welche der drei Flächen kann ich wegwerfen? Hier gibt es verschiedene
Metriken…
Triangulierung in 3D:
Mit Delaunay, allerdings mit Tetraedern Minimaler Winkel in der Tetraeder-Spitze maximieren (Raumwinkel) Problem: welche der drei Flächen kann ich wegwerfen? Hier gibt es verschiedene
Metriken…
Raytracing vs. Rasterisierung
Raytracing:
Strahl aus Kamerazentrum (in Weltkoordinaten) durch Raster einer virtuellen Bildebene. Der Strahl muss gegen die Geometrie auf Schnittpunkte getestet werden. Prinzipiell muss dabei mit jedem Objekt ein Schnitttest durchgeführt werden. Der vorderste Schnittpunkt ist das sichtbare Objekt. In Abhängigkeit der Materialeigenschaften -> Schattenfühler oder Reflexion/ Brechung und Weiterverfolgung
+ bessere Beleuchtung( echte Schatten, Reflexionen, Lichtbrechung
- langsamer, keine Hardware
Rasterisierung:
Transformation der Kamera in Ursprung + perspektivische Projektion
+ sehr performant, da jedes Polygon unabh. von anderen betrachtet werden kann -> parallelisierbar
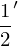
Strahl aus Kamerazentrum (in Weltkoordinaten) durch Raster einer virtuellen Bildebene. Der Strahl muss gegen die Geometrie auf Schnittpunkte getestet werden. Prinzipiell muss dabei mit jedem Objekt ein Schnitttest durchgeführt werden. Der vorderste Schnittpunkt ist das sichtbare Objekt. In Abhängigkeit der Materialeigenschaften -> Schattenfühler oder Reflexion/ Brechung und Weiterverfolgung
+ bessere Beleuchtung( echte Schatten, Reflexionen, Lichtbrechung
- langsamer, keine Hardware
Rasterisierung:
Transformation der Kamera in Ursprung + perspektivische Projektion
+ sehr performant, da jedes Polygon unabh. von anderen betrachtet werden kann -> parallelisierbar
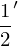
Tags:
Source: http://vokker.net
Source: http://vokker.net
AnSim Inhalte
Die Vorlesung vermittelt die grundlegenden Algorithmen und Verfahren aus den Bereichen der Simulation und Animation. Den Kern bilden dabei Verfahren zur Interpolation von Positionen und Orientierungen im Zusammenhang mit Weg-Zeit-Diagrammen (Animationen), sowie die physikalischen Gesetzmäßigkeiten der Kinetik und Kinematik mit den entsprechenden Simulationsmethoden. Im Vordergrund stehen dabei vor allem echtzeitfähige Verfahren zur Anwendung in Virtuellen Welten oder Computerspielen.
Themenübersicht
Interpolation von Positionen und Orientierung entlang von Kurven
Euler-Winkel, axis-angle und Quaternionen
Grundlagen der Kinetik und Kinematik
Simulation der Dynamik von Massepunkten
Simulation der Dynamik von Festkörpern
Themenübersicht
Interpolation von Positionen und Orientierung entlang von Kurven
Euler-Winkel, axis-angle und Quaternionen
Grundlagen der Kinetik und Kinematik
Simulation der Dynamik von Massepunkten
Simulation der Dynamik von Festkörpern
SE2 Inhalte
Auf der Basis allgemeiner Grundlagen zu informationellen Prozessen und zum Information Retrieval (Teil 1) wird auf die Problematik der Recherche in verteilten Informationsbeständen und auf WWW-Suchmaschinen eingegangen (einschließlich Konzepte von Clearinghouses). Ein weiterer Schwerpunkt (Teil 2) sind die Visualisierungsansätze und -probleme beim Textretrieval und bei der Faktenrecherche, die Integration von Text und Faktenrecherche auf der Basis von Modellen und Theorien des künstlerischen Designs vs. softwareergonomische Ansätze. Visualisierungsansätze mit ihren ästhetischen Anforderungen gewinnen vor allem in Kontext des WWW immer stärker an Bedeutung.
Weitere wichtige Themen waren Ontologien, Kognition und Kognitivität
Weitere wichtige Themen waren Ontologien, Kognition und Kognitivität
Flashcard set info:
Author: cobocards-admin
Main topic: Informatik
Topic: Computergrafik
School / Univ.: Universität Koblenz-Landau
City: Koblenz
Published: 18.10.2010
Card tags:
All cards (107)
no tags




 Raytracing von BVHs, um die Zahl der Schnitttests zu reduzieren:
Raytracing von BVHs, um die Zahl der Schnitttests zu reduzieren:




 Rein gehen Normale, Vertexposition, Farbe und Texturkoordinaten, sowie globale OpenGL-States. Raus gehen transformierte Vertexposition (Modelviewprojection) und Texturkoordinaten, sowie Varying-Variablen und Vertexfarbe.
Rein gehen Normale, Vertexposition, Farbe und Texturkoordinaten, sowie globale OpenGL-States. Raus gehen transformierte Vertexposition (Modelviewprojection) und Texturkoordinaten, sowie Varying-Variablen und Vertexfarbe.


