Welche Eigenschaft hat die Funktion 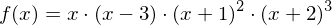 ?
?
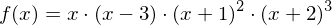 ?
?Die Funktion besitzt eine einfache Nullstelle bei 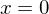 und
und 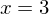 , eine doppelte Nullstelle bei
, eine doppelte Nullstelle bei 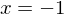 und eine dreifache Nullstelle bei
und eine dreifache Nullstelle bei 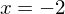 .
.
Das Schaubild schneidet die x-Achse bei den einfachen Nullstellen (lokal nährungsweise wie eine Gerade), es berührt die x-Achse bei der doppelten Nullstellen (näherungsweise wie eine Parabel) und schneidet die x-Achse in einem Sattelpunkt (auch Terassenpunkt) bei der dreifachen Nullstelle (lokal wie einer Parabel dritter Ordnung).
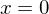 und
und 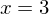 , eine doppelte Nullstelle bei
, eine doppelte Nullstelle bei 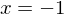 und eine dreifache Nullstelle bei
und eine dreifache Nullstelle bei 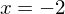 .
.Das Schaubild schneidet die x-Achse bei den einfachen Nullstellen (lokal nährungsweise wie eine Gerade), es berührt die x-Achse bei der doppelten Nullstellen (näherungsweise wie eine Parabel) und schneidet die x-Achse in einem Sattelpunkt (auch Terassenpunkt) bei der dreifachen Nullstelle (lokal wie einer Parabel dritter Ordnung).
Tags: Funktion, Nullstelle, Produktform, Sattelpunkt, Terassenpunkt
Source:
Source:
Was versteht man unter der notwendigen Bedingung für innere Extremstellen.
Bei einer inneren Extremstelle muss die erste Ableitung den Wert null besitzten, denn bei jeder inneren Extremstelle muss das Schaubild eine waagerechte Tangente besitzten.
Allerdings reicht es nicht umgekehrt nicht aus, zur Bestimmung der Extremstellen nur die Nullstellen der Ableitungsfunktion zu betrachten. (Diese sind nur "Kandidaten für Extremstellen".) Es gibt ja noch die Sattel- oder Terassenpunkte.
Aus einer inneren Extremstelle darf man auf die Nullstelle der Ableitungsfunktion schließen, nicht aber umkehrt.
Wir sagen: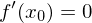 ist notwendig für eine Extremstelle, nicht aber hinreichend.
ist notwendig für eine Extremstelle, nicht aber hinreichend.
Allerdings reicht es nicht umgekehrt nicht aus, zur Bestimmung der Extremstellen nur die Nullstellen der Ableitungsfunktion zu betrachten. (Diese sind nur "Kandidaten für Extremstellen".) Es gibt ja noch die Sattel- oder Terassenpunkte.
Aus einer inneren Extremstelle darf man auf die Nullstelle der Ableitungsfunktion schließen, nicht aber umkehrt.
Wir sagen:
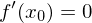 ist notwendig für eine Extremstelle, nicht aber hinreichend.
ist notwendig für eine Extremstelle, nicht aber hinreichend.Tags: Extremstelle, hinreichend, notwendig, Sattelpunkt, Terassenpunkt
Source:
Source:
Welche notwendigen und hinreichenden Bedingungen muss eine (differenzierbare) Funktion erfüllen, wenn beim zugehörigen Schaubild an einer Stelle  ein Sattelpunkt (oder Terassenpunkt) vorliegt?
ein Sattelpunkt (oder Terassenpunkt) vorliegt?
 ein Sattelpunkt (oder Terassenpunkt) vorliegt?
ein Sattelpunkt (oder Terassenpunkt) vorliegt?Bei einem Sattelpunkt (auch Terassenpunkt) muss an der entsprechenden Stelle  die Ableitungsfunktion f' den Wert null besitzten (Sattelpunkte haben waagerechte Tangenten), rechts und links von
die Ableitungsfunktion f' den Wert null besitzten (Sattelpunkte haben waagerechte Tangenten), rechts und links von  muss f' entweder nur positive Werte oder nur negative Werte besitzten.
muss f' entweder nur positive Werte oder nur negative Werte besitzten.
Jede dieser zwei Bedingungen ist notwendig für einen Sattelpunkt - nur wenn beide Bedingungen gleichzeitig erfüllt sind, können wir an dieser Stelle sicher auf einen Sattelpunkt schließen - sie sind hierfür hinreichend.
Ebenfalls hinreichend für einen Sattelpunkt an der Stelle ist die Bedingung, dass sowohl
ist die Bedingung, dass sowohl 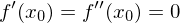 als auch
als auch 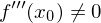 gilt.
gilt.
 die Ableitungsfunktion f' den Wert null besitzten (Sattelpunkte haben waagerechte Tangenten), rechts und links von
die Ableitungsfunktion f' den Wert null besitzten (Sattelpunkte haben waagerechte Tangenten), rechts und links von  muss f' entweder nur positive Werte oder nur negative Werte besitzten.
muss f' entweder nur positive Werte oder nur negative Werte besitzten. Jede dieser zwei Bedingungen ist notwendig für einen Sattelpunkt - nur wenn beide Bedingungen gleichzeitig erfüllt sind, können wir an dieser Stelle sicher auf einen Sattelpunkt schließen - sie sind hierfür hinreichend.
Ebenfalls hinreichend für einen Sattelpunkt an der Stelle
 ist die Bedingung, dass sowohl
ist die Bedingung, dass sowohl 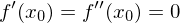 als auch
als auch 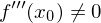 gilt.
gilt.Tags: Begriffe, Funktion, hinreichend, notwendig, Sattelpunkt, Terassenpunkt
Source:
Source:
Flashcard set info:
Author: www.mathematik-bw.de
Main topic: Mathematik
Topic: 10. Klasse
School / Univ.: Clara-Schumann-Gymnasium
City: Lahr
Published: 23.12.2009
Card tags:
All cards (47)
Ableitung (10)
Änderungsrate (9)
Anwendung (2)
Begriffe (17)
Definitionsmenge (1)
Extremstelle (2)
Funktion (8)
ganzrational (5)
Gerade (13)
Grad (1)
h-Methode (6)
hinreichend (3)
Intervalle (1)
Normale (2)
notwendig (2)
Nullstelle (5)
Produktform (3)
Sattelpunkt (3)
Schnittwinkel (1)
Sekante (1)
Sekantensteigung (1)
Steigungswinkel (3)
Streckung (1)
Symmetrie (3)
Tangente (7)
Terassenpunkt (3)
Verschiebung (7)
Wertemenge (1)



