Gib die Definitions- und Wertemengen von der Quadrat, der Kehrwert- und der Wurzelfunktion in zwei verschiedenen Intervallschreibweisen an.
Quadratfunktion:
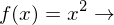
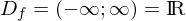
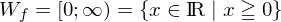
Kehrwertfunktion:
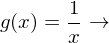
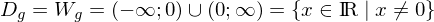
Wurzelfunktion:
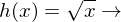
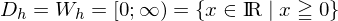
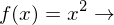
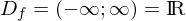
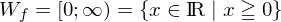
Kehrwertfunktion:
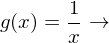
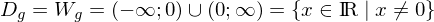
Wurzelfunktion:
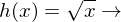
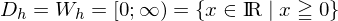
Tags: Definitionsmenge, Funktion, Intervalle, Wertemenge
Source:
Source:
Skizziere die Schaubilder der Kehrwertfunktion, der Quadratfunktion und der Wurzelfunktion.
Wie nennt man das Schaubild der Kehrwertfunktion?
Was ist eine „Antiproportionalität“?
Wie nennt man das Schaubild der Kehrwertfunktion?
Was ist eine „Antiproportionalität“?
Antwort 
Schaubild der Kehrwertfunktion heißt Hyperbel: blau
Schaubild der Quadratfunktion (heißt Nomalparabel): rot
Schaubild der Wurzelfunktion: grün
Eine Antiproportionalität ist eine „gestreckte“ Kehrwertfunktion. Das Verdoppeln des x-Wertes bewirkt stets eine Halbierung des entsprechenden Funktionswertes.
Linktipp: Die wichtigsten Funktionen mit ihren Schaubildern

Schaubild der Kehrwertfunktion heißt Hyperbel: blau
Schaubild der Quadratfunktion (heißt Nomalparabel): rot
Schaubild der Wurzelfunktion: grün
Eine Antiproportionalität ist eine „gestreckte“ Kehrwertfunktion. Das Verdoppeln des x-Wertes bewirkt stets eine Halbierung des entsprechenden Funktionswertes.
Linktipp: Die wichtigsten Funktionen mit ihren Schaubildern
Tags: Begriffe, Funktion
Source:
Source:
Bei einer Funktion f gilt für alle 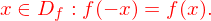
Was bedeutet dies für das zugehörige Schaubild?
Nenne drei unterschiedliche Funktionstypen mit dieser Eigenschaft in der allgemeinen Form.
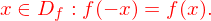
Was bedeutet dies für das zugehörige Schaubild?
Nenne drei unterschiedliche Funktionstypen mit dieser Eigenschaft in der allgemeinen Form.
Aus der Bedingung folgt die (Achsen-)Symmetrie des Schaubildes von f zur y-Achse
Beachte, dass man die entsprechende Funktion als "gerade" bezeichnet - nicht aber das Schaubild!
Beispiele:
- Jede konstante Funktion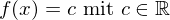
- Potenzfunktionen mit gerader, ganzzahligen Hochzahl:
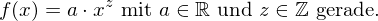
- Jede ganzrationale Funktion mit ausschließlich geraden
"x-Potenzen" .
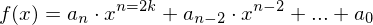
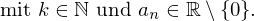
- Die Kosinusfunktion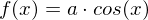 mit beliebigem
mit beliebigem
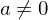 .
.
- Die Nullfunktion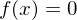 . (Einzige Funktion die sowohl
. (Einzige Funktion die sowohl
gerade, als auch ungerade ist.)
Bemerkungen:
In Worten bedeutet die obige Gleichung: "Betrachtet man
auf der x-Achse eine Zahl und ihre Gegenzahl, so sind auch die entsprechenden y-Werte identisch."
Gerade Zahlen haben immer die Form eines Produkt aus einer natürlichen Zahl mit 2.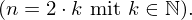
Beachte, dass man die entsprechende Funktion als "gerade" bezeichnet - nicht aber das Schaubild!
Beispiele:
- Jede konstante Funktion
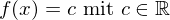
- Potenzfunktionen mit gerader, ganzzahligen Hochzahl:
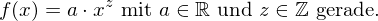
- Jede ganzrationale Funktion mit ausschließlich geraden
"x-Potenzen" .
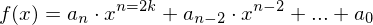
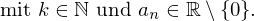
- Die Kosinusfunktion
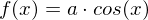 mit beliebigem
mit beliebigem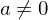 .
.- Die Nullfunktion
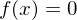 . (Einzige Funktion die sowohl
. (Einzige Funktion die sowohlgerade, als auch ungerade ist.)
Bemerkungen:
In Worten bedeutet die obige Gleichung: "Betrachtet man
auf der x-Achse eine Zahl und ihre Gegenzahl, so sind auch die entsprechenden y-Werte identisch."
Gerade Zahlen haben immer die Form eines Produkt aus einer natürlichen Zahl mit 2.
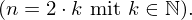
Tags: Begriffe, Funktion, ganzrational, Symmetrie
Source:
Source:
Bei einer Funktion f gilt für alle 
Was bedeutet dies für das zugehörige Schaubild?
Nenne drei unterschiedliche Funktionstypen mit dieser Eigenschaft in der allgemeinen Form.

Was bedeutet dies für das zugehörige Schaubild?
Nenne drei unterschiedliche Funktionstypen mit dieser Eigenschaft in der allgemeinen Form.
Aus der Bedingung folgt die Punktsymmetrie des Schaubildes von f zum Ursprung
Beachte, dass man die entsprechende Funktion als "ungerade" bezeichnet - nicht aber das Schaubild!
Beispiele:
- Jede Proportionalität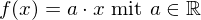 oder
oder
allg. Potenzfktn. mit ungerader, ganzzahliger Hochzahl
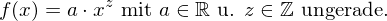 .
.
Hierzu zählt auch die Kehrwertfunktion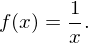
- Jede ganzrationale Funktion mit ausschließlich ungeraden
"x-Potenzen"
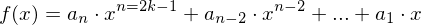
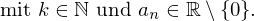
- Die Sinusfunktion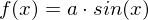 mit beliebigem
mit beliebigem
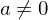 .
.
- Die Nullfunktion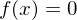 . (Einzige Funktion die sowohl
. (Einzige Funktion die sowohl
gerade, als auch ungerade ist.)
Bemerkungen:
In Worten bedeutet die obige Gleichung: "Betrachtet man
auf der x-Achse eine Zahl und ihre Gegenzahl, so sind auch die entsprechenden y-Werte jeweils Zahl und Gegenzahl."
Ungerade Zahlen haben immer die Form eines Produkt aus einer natürlichen Zahl mit 2 abzüglich oder zuzüglich 1.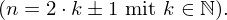
Beachte, dass man die entsprechende Funktion als "ungerade" bezeichnet - nicht aber das Schaubild!
Beispiele:
- Jede Proportionalität
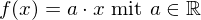 oder
oder allg. Potenzfktn. mit ungerader, ganzzahliger Hochzahl
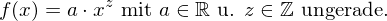 .
. Hierzu zählt auch die Kehrwertfunktion
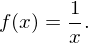
- Jede ganzrationale Funktion mit ausschließlich ungeraden
"x-Potenzen"
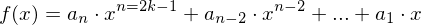
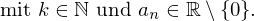
- Die Sinusfunktion
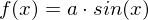 mit beliebigem
mit beliebigem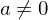 .
.- Die Nullfunktion
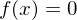 . (Einzige Funktion die sowohl
. (Einzige Funktion die sowohlgerade, als auch ungerade ist.)
Bemerkungen:
In Worten bedeutet die obige Gleichung: "Betrachtet man
auf der x-Achse eine Zahl und ihre Gegenzahl, so sind auch die entsprechenden y-Werte jeweils Zahl und Gegenzahl."
Ungerade Zahlen haben immer die Form eines Produkt aus einer natürlichen Zahl mit 2 abzüglich oder zuzüglich 1.
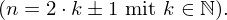
Tags: Begriffe, Funktion, ganzrational, Symmetrie
Source:
Source:
Überprüfe, ob das Schaubild der Funktion 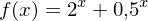 punktsymmetrisch zum Ursprung oder symmetrisch zur y-Achse ist.
punktsymmetrisch zum Ursprung oder symmetrisch zur y-Achse ist.
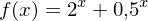 punktsymmetrisch zum Ursprung oder symmetrisch zur y-Achse ist.
punktsymmetrisch zum Ursprung oder symmetrisch zur y-Achse ist.Die Funktion f ist für alle reelen Zahlen definiert. Für jedes x gilt:
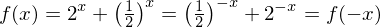
Somit ist die Funktion f gerade und das zugehörige Schaubild ist symmetrisch zur y-Achse.

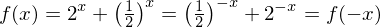
Somit ist die Funktion f gerade und das zugehörige Schaubild ist symmetrisch zur y-Achse.

Tags: Funktion, Symmetrie
Source:
Source:
Welche Eigenschaft hat die Funktion 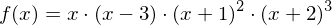 ?
?
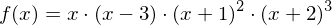 ?
?Die Funktion besitzt eine einfache Nullstelle bei 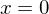 und
und 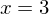 , eine doppelte Nullstelle bei
, eine doppelte Nullstelle bei 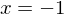 und eine dreifache Nullstelle bei
und eine dreifache Nullstelle bei 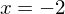 .
.
Das Schaubild schneidet die x-Achse bei den einfachen Nullstellen (lokal nährungsweise wie eine Gerade), es berührt die x-Achse bei der doppelten Nullstellen (näherungsweise wie eine Parabel) und schneidet die x-Achse in einem Sattelpunkt (auch Terassenpunkt) bei der dreifachen Nullstelle (lokal wie einer Parabel dritter Ordnung).
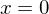 und
und 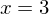 , eine doppelte Nullstelle bei
, eine doppelte Nullstelle bei 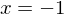 und eine dreifache Nullstelle bei
und eine dreifache Nullstelle bei 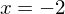 .
.Das Schaubild schneidet die x-Achse bei den einfachen Nullstellen (lokal nährungsweise wie eine Gerade), es berührt die x-Achse bei der doppelten Nullstellen (näherungsweise wie eine Parabel) und schneidet die x-Achse in einem Sattelpunkt (auch Terassenpunkt) bei der dreifachen Nullstelle (lokal wie einer Parabel dritter Ordnung).
Tags: Funktion, Nullstelle, Produktform, Sattelpunkt, Terassenpunkt
Source:
Source:
Finde eine Funktion deren Schaubild an der Stelle 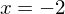 und die x-Achse durchschneidet, an der Stelle
und die x-Achse durchschneidet, an der Stelle 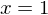 die x-Achse berührt und die y-Achse im Punkt (0/6) schneidet.
die x-Achse berührt und die y-Achse im Punkt (0/6) schneidet.
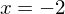 und die x-Achse durchschneidet, an der Stelle
und die x-Achse durchschneidet, an der Stelle 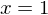 die x-Achse berührt und die y-Achse im Punkt (0/6) schneidet.
die x-Achse berührt und die y-Achse im Punkt (0/6) schneidet.Für die Lösung dieser Aufgabe benötigt man nicht unbedingt die Differenzialrechnung.
Die einfache Nullstelle liefert den Faktor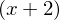 , die doppelte Nullstelle (bei x=1) entsprechend
, die doppelte Nullstelle (bei x=1) entsprechend 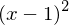 . Hieraus ergibt sich eine (Hilfs-)Funktion
. Hieraus ergibt sich eine (Hilfs-)Funktion 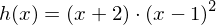 , die wir so in y-Richtung strecken, dass das Schaubild der gestreckten Funktion durch (0/6) verläuft.
, die wir so in y-Richtung strecken, dass das Schaubild der gestreckten Funktion durch (0/6) verläuft. 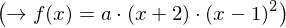
Aus (0/6) folgt: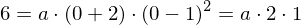
also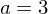 .
.
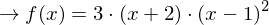
(Bei f(x) handelt es sich um eine ganzrationale Funktion, aber eine Darstellung in Summenform ist nicht gefordert! Kontrolliere das Ergebnis mit dem GTR/CAS.)
Die einfache Nullstelle liefert den Faktor
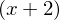 , die doppelte Nullstelle (bei x=1) entsprechend
, die doppelte Nullstelle (bei x=1) entsprechend 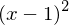 . Hieraus ergibt sich eine (Hilfs-)Funktion
. Hieraus ergibt sich eine (Hilfs-)Funktion 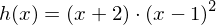 , die wir so in y-Richtung strecken, dass das Schaubild der gestreckten Funktion durch (0/6) verläuft.
, die wir so in y-Richtung strecken, dass das Schaubild der gestreckten Funktion durch (0/6) verläuft. 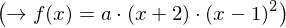
Aus (0/6) folgt:
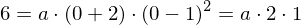
also
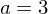 .
.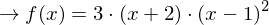
(Bei f(x) handelt es sich um eine ganzrationale Funktion, aber eine Darstellung in Summenform ist nicht gefordert! Kontrolliere das Ergebnis mit dem GTR/CAS.)
Tags: Funktion, ganzrational, Nullstelle, Produktform, Streckung
Source:
Source:
Welche notwendigen und hinreichenden Bedingungen muss eine (differenzierbare) Funktion erfüllen, wenn beim zugehörigen Schaubild an einer Stelle  ein Sattelpunkt (oder Terassenpunkt) vorliegt?
ein Sattelpunkt (oder Terassenpunkt) vorliegt?
 ein Sattelpunkt (oder Terassenpunkt) vorliegt?
ein Sattelpunkt (oder Terassenpunkt) vorliegt?Bei einem Sattelpunkt (auch Terassenpunkt) muss an der entsprechenden Stelle  die Ableitungsfunktion f' den Wert null besitzten (Sattelpunkte haben waagerechte Tangenten), rechts und links von
die Ableitungsfunktion f' den Wert null besitzten (Sattelpunkte haben waagerechte Tangenten), rechts und links von  muss f' entweder nur positive Werte oder nur negative Werte besitzten.
muss f' entweder nur positive Werte oder nur negative Werte besitzten.
Jede dieser zwei Bedingungen ist notwendig für einen Sattelpunkt - nur wenn beide Bedingungen gleichzeitig erfüllt sind, können wir an dieser Stelle sicher auf einen Sattelpunkt schließen - sie sind hierfür hinreichend.
Ebenfalls hinreichend für einen Sattelpunkt an der Stelle ist die Bedingung, dass sowohl
ist die Bedingung, dass sowohl 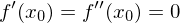 als auch
als auch 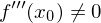 gilt.
gilt.
 die Ableitungsfunktion f' den Wert null besitzten (Sattelpunkte haben waagerechte Tangenten), rechts und links von
die Ableitungsfunktion f' den Wert null besitzten (Sattelpunkte haben waagerechte Tangenten), rechts und links von  muss f' entweder nur positive Werte oder nur negative Werte besitzten.
muss f' entweder nur positive Werte oder nur negative Werte besitzten. Jede dieser zwei Bedingungen ist notwendig für einen Sattelpunkt - nur wenn beide Bedingungen gleichzeitig erfüllt sind, können wir an dieser Stelle sicher auf einen Sattelpunkt schließen - sie sind hierfür hinreichend.
Ebenfalls hinreichend für einen Sattelpunkt an der Stelle
 ist die Bedingung, dass sowohl
ist die Bedingung, dass sowohl 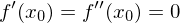 als auch
als auch 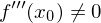 gilt.
gilt.Tags: Begriffe, Funktion, hinreichend, notwendig, Sattelpunkt, Terassenpunkt
Source:
Source:
Flashcard set info:
Author: www.mathematik-bw.de
Main topic: Mathematik
Topic: 10. Klasse
School / Univ.: Clara-Schumann-Gymnasium
City: Lahr
Published: 23.12.2009
Card tags:
All cards (47)
Ableitung (10)
Änderungsrate (9)
Anwendung (2)
Begriffe (17)
Definitionsmenge (1)
Extremstelle (2)
Funktion (8)
ganzrational (5)
Gerade (13)
Grad (1)
h-Methode (6)
hinreichend (3)
Intervalle (1)
Normale (2)
notwendig (2)
Nullstelle (5)
Produktform (3)
Sattelpunkt (3)
Schnittwinkel (1)
Sekante (1)
Sekantensteigung (1)
Steigungswinkel (3)
Streckung (1)
Symmetrie (3)
Tangente (7)
Terassenpunkt (3)
Verschiebung (7)
Wertemenge (1)



