Welche Steigung m besitzt die Gerade durch die Punkte P(-3/-5) und Q(7/21)?
Die Steigung erhält man über das Verhältnis "Hochwert durch Rechtswert" bei einem (beliebigen) Steigungsdreieck. Durch die Differenzen der Punktkoordinaten erhalten wir solch ein Steigungsdreick.
Tipps:
1. Ziehe immer von den Koordianten des rechten Punkts die
Koordinaten des linken Punktes ab. (Dann ist der Nenner bei
der Steigung positiv.)
2. Kontrolliere das Ergebniss durch Überschlag.
Die Steigung muss postiv sein, wenn der rechte Punkt über
dem linken liegt.
Schaubilder mit betragsmäßig kleinen Steigungen
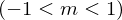verlaufen "flach".
Hier:
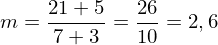
Kontrolle durch Überschlag:
Die y-Koordinaten der Geradepunkte steigen stark an (pro Einheit nach rechts um 2,6).
Tipps:
1. Ziehe immer von den Koordianten des rechten Punkts die
Koordinaten des linken Punktes ab. (Dann ist der Nenner bei
der Steigung positiv.)
2. Kontrolliere das Ergebniss durch Überschlag.
Die Steigung muss postiv sein, wenn der rechte Punkt über
dem linken liegt.
Schaubilder mit betragsmäßig kleinen Steigungen
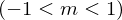verlaufen "flach".Hier:
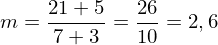
Kontrolle durch Überschlag:
Die y-Koordinaten der Geradepunkte steigen stark an (pro Einheit nach rechts um 2,6).
Tags: Gerade
Source:
Source:
Wie lautet die Gleichung der Geraden, die zur x-Achse parallel verläuft und die y-Achse im Punkt (0/-2) schneidet?
Welche gemeinsame Eigenschaft besitzten alle Punkte auf dieser Geraden?
Lässt sich zu dieser Geraden eine Funktionsgleichgung aufstellen? Begründe!
Welche gemeinsame Eigenschaft besitzten alle Punkte auf dieser Geraden?
Lässt sich zu dieser Geraden eine Funktionsgleichgung aufstellen? Begründe!
Die Geradengleichung lautet: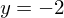 
.
Jeder Punkt auf dieser Geraden besitzt die y-Koordinate -2.
Jedem x-Wert wird genau ein y-Wert zugeordnet. Damit lautet die Funktionsgleichung: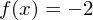
(konstante Funktion).
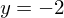.Jeder Punkt auf dieser Geraden besitzt die y-Koordinate -2.
Jedem x-Wert wird genau ein y-Wert zugeordnet. Damit lautet die Funktionsgleichung:
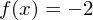(konstante Funktion).Tags: Gerade
Source:
Source:
Wie lautet die Gleichung der Geraden, die zur y-Achse parallel verläuft und die x-Achse an der Stelle x=4 schneidet?
Welche gemeinsame Eigenschaft besitzten alle Punkte auf dieser Geraden?
Lässt sich zu dieser Geraden eine Funktionsgleichgung aufstellen? Begründe!
Welche gemeinsame Eigenschaft besitzten alle Punkte auf dieser Geraden?
Lässt sich zu dieser Geraden eine Funktionsgleichgung aufstellen? Begründe!
Die Geradengleichung lautet: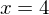 
.
Jeder Punkt auf dieser Geraden besitzt die x-Koordinate 4.
Zu dieser Geraden kann man keine Funktionsgleichung aufstellen. Bei einer Funktion wird eine eindeutige Zuordnung gefordert, bei der jedem x-Wert aus der Definitionsmenge genau ein y-Wert zugeordnet wird. Hier werden dem x-Wert 4 unendlich viele y-Werte zugeordnet - die Eindeutigkeit wird dadurch verletzt.
Zu den Parallelen zur y-Achse können wir nur Geradengleichungen- aber keine Funktionsgleichungen aufstellen.
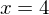.Jeder Punkt auf dieser Geraden besitzt die x-Koordinate 4.
Zu dieser Geraden kann man keine Funktionsgleichung aufstellen. Bei einer Funktion wird eine eindeutige Zuordnung gefordert, bei der jedem x-Wert aus der Definitionsmenge genau ein y-Wert zugeordnet wird. Hier werden dem x-Wert 4 unendlich viele y-Werte zugeordnet - die Eindeutigkeit wird dadurch verletzt.
Zu den Parallelen zur y-Achse können wir nur Geradengleichungen- aber keine Funktionsgleichungen aufstellen.
Tags: Gerade
Source:
Source:
Was versteht man unter "orthogonal"?
Wie lautet die "Orthogonalitätsbedingung" bei Geradensteigungen? Gib die Gleichung an und formuliere den Zusammenhang in einem Satz.
Wo wird die Orthoganlitätsbedingung benötigt?
Wie lautet die "Orthogonalitätsbedingung" bei Geradensteigungen? Gib die Gleichung an und formuliere den Zusammenhang in einem Satz.
Wo wird die Orthoganlitätsbedingung benötigt?
"Orthogonal" ist ein Synonym zu "rechtwinklig".
Die Orthogonalitätsbedingung lautet: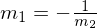
oder 
.
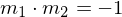Dies bedeutet, dass bei zwei zueinander senkrecht stehenden Geraden die eine Steigung genau die Gegenzahl des Kehrwertes der anderen Steigung ist.
(Z. B. ist zu einer Geraden mit der Steigung 2 jede Gerade orthogonal, die die Steigung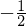
besitzt.)
Die Orthogonalitätsbediung wird beim Zusammenhang von Tangenten und Normalen benötigt.
Die Orthogonalitätsbedingung lautet:
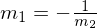oder 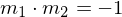.Dies bedeutet, dass bei zwei zueinander senkrecht stehenden Geraden die eine Steigung genau die Gegenzahl des Kehrwertes der anderen Steigung ist.
(Z. B. ist zu einer Geraden mit der Steigung 2 jede Gerade orthogonal, die die Steigung
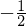besitzt.)Die Orthogonalitätsbediung wird beim Zusammenhang von Tangenten und Normalen benötigt.
Tags: Gerade, Normale, Tangente
Source:
Source:
Wie muss man den Funktionsterm einer Funktion verändern, wenn das Schaubild um a Längeneinheiten in x-Richtung verschoben wird?
Wie lautet f(x), wenn das Schaubild durch Verschiebung um 3 LE in x-Richtung aus einer Normalparabel hervorgeht?
Wie lautet f(x), wenn das Schaubild durch Verschiebung um 3 LE in x-Richtung aus einer Normalparabel hervorgeht?
Bei einer Verschiebung um a Längeneinheiten in x-Richtung muss man jedes x im Funktionsterm durch den Ausdruck (x-a) ersetzten.
(Falls a negativ ist muss man in der Klammer natürlich den Betrag von a addieren.)
Zur verschobenen Normalparabel wir aus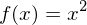
.
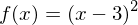Animation auf dem Landesbildungsserver Baden-Württemberg
(Falls a negativ ist muss man in der Klammer natürlich den Betrag von a addieren.)
Zur verschobenen Normalparabel wir aus
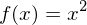
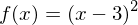.Animation auf dem Landesbildungsserver Baden-Württemberg
Tags: Gerade, Verschiebung
Source:
Source:
Wie muss man den Funktionsterm einer Funktion verändern, wenn das Schaubild um b Längeneinheiten in y-Richtung verschoben wird?
Wie lautet f(x), wenn das Schaubild durch Verschiebung um 1,5 LE in y-Richtung aus einer Normalparabel hervorgeht?
Wie lautet f(x), wenn das Schaubild durch Verschiebung um 1,5 LE in y-Richtung aus einer Normalparabel hervorgeht?
Bei einer Verschiebung um b Längeneinheiten in y-Richtung muss zum "alten" Funktionsterm die Verschiebung b addieren.
(Falls b negativ ist, muss man natürlich den Betrag von b subtrahieren.)
Zur verschobenen Normalparabel wir aus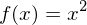 
.
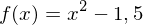Animation auf dem Landesbildungsserver Baden-Württemberg
(Falls b negativ ist, muss man natürlich den Betrag von b subtrahieren.)
Zur verschobenen Normalparabel wir aus
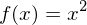
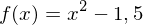.Animation auf dem Landesbildungsserver Baden-Württemberg
Tags: Gerade, Verschiebung
Source:
Source:
Bestimme eine Geradengleichung zur Geraden mit der Steigung 1/3 durch den Punkt P(-3/7).
Verschiebe hierzu eine Ursprungsgerade.
Verschiebe hierzu eine Ursprungsgerade.
Die Ursprungsgerade mit der Steigung 1/3 besitzt die Geradengleichung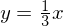 
.
Durch Verschiebung in x-Richtung bis zur x-Koordinate von P wird hieraus: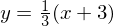
.
Schließlich erhalten wir durch eine weitere Verschiebung zur y-Koordinate von P: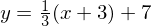
.
Nicht gefordert ist hier die Umformung zur Hauptform einer Geradengleichung (mit dem y-Achsenabschnitt). Diese erhält man durch Ausmultiplizieren: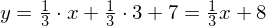
.
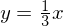. Durch Verschiebung in x-Richtung bis zur x-Koordinate von P wird hieraus:
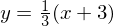. Schließlich erhalten wir durch eine weitere Verschiebung zur y-Koordinate von P:
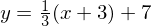. Nicht gefordert ist hier die Umformung zur Hauptform einer Geradengleichung (mit dem y-Achsenabschnitt). Diese erhält man durch Ausmultiplizieren:
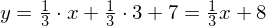. Tags: Gerade, Verschiebung
Source:
Source:
Die Gerade g besitzt die Gleichung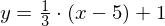 
. Gib die Gleichung der Geraden h an, welche senkrecht zu g durch den Punkt 
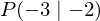verläuft.
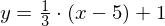. Gib die Gleichung der Geraden h an, welche senkrecht zu g durch den Punkt 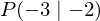verläuft.Geradengleichung von h: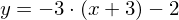 
.
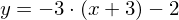. Tags: Gerade, Verschiebung
Source:
Source:
Welcher Zusammenhang besteht zwischen dem Steigungswinkel einer Geraden und deren Steigung?
Welchen Steigungswinkel hat eine Gerade mit der Steigung 1?
Welche Werte kann ein Steigungswinkel annehmen?
Welchen Steigungswinkel hat eine Gerade mit der Steigung 1?
Welche Werte kann ein Steigungswinkel annehmen?
Mit Hilfe der Tangensbeziehung am rechtwinkligen Dreieck folgt aus dem Steigungsdreieck für den Steigungswinkel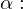 
.
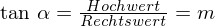Bei einer Geraden mit der Steigung eins ist das Verhältnis aus Hochwert zu Rechtswert bei jedem Steigungsdreieck 1. Der Steigungswinkel ist hierbei Basiswinkel eines rechtwinklig gleichschenkligen Dreiecks und somit gleich 45°.
Steigungswinkel können Werte zwischen -90° und +90° annehmen. (Bei +/-90° ist die Geradensteigung nicht definiert, da die Gerade parallel zur y-Achse verläuft - der Rechtswert bei allen Steigungsdreiecken ist hier 0!)
(Lässt man keine negativen Steigungswinkel zu, liegen die Steigungswinkel zwischen 0° und 180°, wobei die Steigungen der Geraden ab 90° negativ verlaufen.)
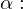
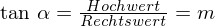.Bei einer Geraden mit der Steigung eins ist das Verhältnis aus Hochwert zu Rechtswert bei jedem Steigungsdreieck 1. Der Steigungswinkel ist hierbei Basiswinkel eines rechtwinklig gleichschenkligen Dreiecks und somit gleich 45°.
Steigungswinkel können Werte zwischen -90° und +90° annehmen. (Bei +/-90° ist die Geradensteigung nicht definiert, da die Gerade parallel zur y-Achse verläuft - der Rechtswert bei allen Steigungsdreiecken ist hier 0!)
(Lässt man keine negativen Steigungswinkel zu, liegen die Steigungswinkel zwischen 0° und 180°, wobei die Steigungen der Geraden ab 90° negativ verlaufen.)
Tags: Begriffe, Gerade, Steigungswinkel
Source:
Source:
Woran erkennt man bereits an den Punktkoordinaten zweier Geradenpunkte, ob der Steigungswinkel der Geraden negativ ist?
Liegt der y-Wert des rechten Punktes unterhalb des y-Wertes des linken, dann "fällt die Gerade an". Der Steigungswinkel (und die Steigung) ist in diesen Fällen negativ.
Tags: Begriffe, Gerade, Steigungswinkel
Source:
Source:
Wie bestimmt man den Schnittwinkel zwischen zwei Geraden?
Erstelle zunächst eine Skizze!
Bestimme die Steigungswinkel zu jeder einzelnen Geraden und errechne hieraus den Wert für die Steigungswinkel beider Geraden.
Beachte, dass man je nach Lage der Geraden die Steigungswinkel addieren bzw. voneinander subtrahieren muss. Aus diesem Grund ist bei dieser Aufgabenstellung eine Skizze unbedingt zu empfehlen.
Linktipp: Landesbildungsserver Baden-Württemberg
Bestimme die Steigungswinkel zu jeder einzelnen Geraden und errechne hieraus den Wert für die Steigungswinkel beider Geraden.
Beachte, dass man je nach Lage der Geraden die Steigungswinkel addieren bzw. voneinander subtrahieren muss. Aus diesem Grund ist bei dieser Aufgabenstellung eine Skizze unbedingt zu empfehlen.
Linktipp: Landesbildungsserver Baden-Württemberg
Tags: Begriffe, Gerade, Schnittwinkel, Steigungswinkel
Source:
Source:
An welcher Stelle hat die Tangente an die Normalparabel die gleiche Steigung wie die Gerade mit der Gleichung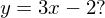 
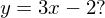
Die Gerade besitzt die Steigung 3. Gesucht ist daher die Stelle (x-Wert), bei dem die Normalparabel die Steigung 3 hat.
Die Funktion zur Normalparabel lautet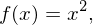
die zugehörige Die zugehörige Ableitungsfunktion liefert die Tangentensteigungen: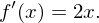 
Löse die Gleichung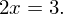
Antwort: An der Stelle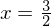
hat die Tangente an die Normalparabel die gleiche Steigung wie die genannte Gerade.
Die Funktion zur Normalparabel lautet
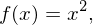die zugehörige Die zugehörige Ableitungsfunktion liefert die Tangentensteigungen: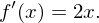 Löse die Gleichung
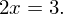
Antwort: An der Stelle
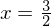hat die Tangente an die Normalparabel die gleiche Steigung wie die genannte Gerade.Tags: Gerade, Tangente
Source:
Source:
Wie lauten die Gleichungen der Tangenen und der Normalen an die Normalparabel an der Stelle x=1,5?
Zugehörige Funktion: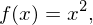 
Tangentensteigung aus Ableitungsfunktion 
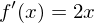somit beträgt die Tangentsteigung an der Stelle 1,5: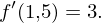 
Der y-Wert an der Stelle 1,5 ist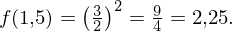
Verschiebt man eine Ursprungsgerade mit der Steigung 3 um 1,5 in x-Richtung und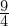
in y-Richtung erhält man die gesuchte Tangente. Ihre Gleichung lautet:
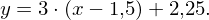
Aufgrund der Orthogonalitätsbedingung folgt für die Gleichung der zugehörigen Normalen:
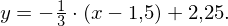
Hinweis:
In der Hauptform (mit Steigung und y-Achsenabschnitt) lauten die Gleichungen:
Tangente: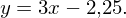
Normale: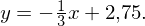
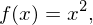Tangentensteigung aus Ableitungsfunktion 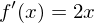somit beträgt die Tangentsteigung an der Stelle 1,5: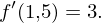 Der y-Wert an der Stelle 1,5 ist
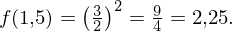
Verschiebt man eine Ursprungsgerade mit der Steigung 3 um 1,5 in x-Richtung und
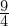in y-Richtung erhält man die gesuchte Tangente. Ihre Gleichung lautet: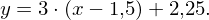 Aufgrund der Orthogonalitätsbedingung folgt für die Gleichung der zugehörigen Normalen:
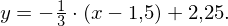
Hinweis:
In der Hauptform (mit Steigung und y-Achsenabschnitt) lauten die Gleichungen:
Tangente:
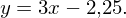
Normale:
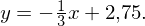
Tags: Gerade, Normale, Tangente, Verschiebung
Source:
Source:
Flashcard set info:
Author: www.mathematik-bw.de
Main topic: Mathematik
Topic: 10. Klasse
School / Univ.: Clara-Schumann-Gymnasium
City: Lahr
Published: 23.12.2009
Card tags:
All cards (47)
Ableitung (10)
Änderungsrate (9)
Anwendung (2)
Begriffe (17)
Definitionsmenge (1)
Extremstelle (2)
Funktion (8)
ganzrational (5)
Gerade (13)
Grad (1)
h-Methode (6)
hinreichend (3)
Intervalle (1)
Normale (2)
notwendig (2)
Nullstelle (5)
Produktform (3)
Sattelpunkt (3)
Schnittwinkel (1)
Sekante (1)
Sekantensteigung (1)
Steigungswinkel (3)
Streckung (1)
Symmetrie (3)
Tangente (7)
Terassenpunkt (3)
Verschiebung (7)
Wertemenge (1)
