Was versteht man unter "orthogonal"?
Wie lautet die "Orthogonalitätsbedingung" bei Geradensteigungen? Gib die Gleichung an und formuliere den Zusammenhang in einem Satz.
Wo wird die Orthoganlitätsbedingung benötigt?
Wie lautet die "Orthogonalitätsbedingung" bei Geradensteigungen? Gib die Gleichung an und formuliere den Zusammenhang in einem Satz.
Wo wird die Orthoganlitätsbedingung benötigt?
"Orthogonal" ist ein Synonym zu "rechtwinklig".
Die Orthogonalitätsbedingung lautet: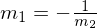 oder
oder 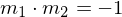 .
.
Dies bedeutet, dass bei zwei zueinander senkrecht stehenden Geraden die eine Steigung genau die Gegenzahl des Kehrwertes der anderen Steigung ist.
(Z. B. ist zu einer Geraden mit der Steigung 2 jede Gerade orthogonal, die die Steigung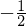 besitzt.)
besitzt.)
Die Orthogonalitätsbediung wird beim Zusammenhang von Tangenten und Normalen benötigt.
Die Orthogonalitätsbedingung lautet:
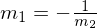 oder
oder 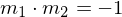 .
.Dies bedeutet, dass bei zwei zueinander senkrecht stehenden Geraden die eine Steigung genau die Gegenzahl des Kehrwertes der anderen Steigung ist.
(Z. B. ist zu einer Geraden mit der Steigung 2 jede Gerade orthogonal, die die Steigung
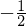 besitzt.)
besitzt.)Die Orthogonalitätsbediung wird beim Zusammenhang von Tangenten und Normalen benötigt.
Tags: Gerade, Normale, Tangente
Quelle:
Quelle:
Nenne drei mögliche Bedeutungen der Ableitung.
1. Grenzwert des Differenzenquotienten (Definition der Ableitung).
2. Steigung der Tangenten an das Schaubild.
3. Momentane oder lokale Änderungsrate.
2. Steigung der Tangenten an das Schaubild.
3. Momentane oder lokale Änderungsrate.
Tags: Ableitung, Änderungsrate, Differenzenquotient, Tangente
Quelle:
Quelle:
An welcher Stelle hat die Tangente an die Normalparabel die gleiche Steigung wie die Gerade mit der Gleichung 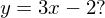
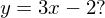
Die Gerade besitzt die Steigung 3. Gesucht ist daher die Stelle (x-Wert), bei dem die Normalparabel die Steigung 3 hat.
Die Funktion zur Normalparabel lautet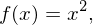 die zugehörige Die zugehörige Ableitungsfunktion liefert die Tangentensteigungen:
die zugehörige Die zugehörige Ableitungsfunktion liefert die Tangentensteigungen: 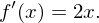
Löse die Gleichung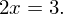
Antwort: An der Stelle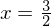 hat die Tangente an die Normalparabel die gleiche Steigung wie die genannte Gerade.
hat die Tangente an die Normalparabel die gleiche Steigung wie die genannte Gerade.
Die Funktion zur Normalparabel lautet
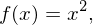 die zugehörige Die zugehörige Ableitungsfunktion liefert die Tangentensteigungen:
die zugehörige Die zugehörige Ableitungsfunktion liefert die Tangentensteigungen: 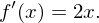
Löse die Gleichung
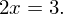
Antwort: An der Stelle
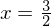 hat die Tangente an die Normalparabel die gleiche Steigung wie die genannte Gerade.
hat die Tangente an die Normalparabel die gleiche Steigung wie die genannte Gerade.Tags: Gerade, Tangente
Quelle:
Quelle:
Wie lauten die Gleichungen der Tangenen und der Normalen an die Normalparabel an der Stelle x=1,5?
Zugehörige Funktion: 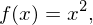 Tangentensteigung aus Ableitungsfunktion
Tangentensteigung aus Ableitungsfunktion 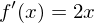 somit beträgt die Tangentsteigung an der Stelle 1,5:
somit beträgt die Tangentsteigung an der Stelle 1,5: 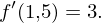
Der y-Wert an der Stelle 1,5 ist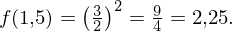
Verschiebt man eine Ursprungsgerade mit der Steigung 3 um 1,5 in x-Richtung und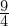 in y-Richtung erhält man die gesuchte Tangente. Ihre Gleichung lautet:
in y-Richtung erhält man die gesuchte Tangente. Ihre Gleichung lautet:
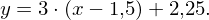
Aufgrund der Orthogonalitätsbedingung folgt für die Gleichung der zugehörigen Normalen:
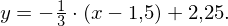
Hinweis:
In der Hauptform (mit Steigung und y-Achsenabschnitt) lauten die Gleichungen:
Tangente: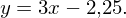
Normale: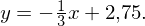

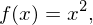 Tangentensteigung aus Ableitungsfunktion
Tangentensteigung aus Ableitungsfunktion 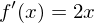 somit beträgt die Tangentsteigung an der Stelle 1,5:
somit beträgt die Tangentsteigung an der Stelle 1,5: 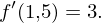
Der y-Wert an der Stelle 1,5 ist
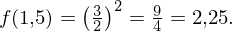
Verschiebt man eine Ursprungsgerade mit der Steigung 3 um 1,5 in x-Richtung und
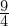 in y-Richtung erhält man die gesuchte Tangente. Ihre Gleichung lautet:
in y-Richtung erhält man die gesuchte Tangente. Ihre Gleichung lautet: 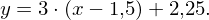
Aufgrund der Orthogonalitätsbedingung folgt für die Gleichung der zugehörigen Normalen:
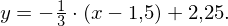
Hinweis:
In der Hauptform (mit Steigung und y-Achsenabschnitt) lauten die Gleichungen:
Tangente:
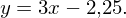
Normale:
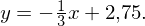

Tags: Gerade, Normale, Tangente, Verschiebung
Quelle:
Quelle:
Wie löst man das folgende Tangentenproblem (Typ 1):
Ein Punkt auf dem Schaubild ist gegeben. Gesucht ist die Tangente in diesem Punkt.
Ein Punkt auf dem Schaubild ist gegeben. Gesucht ist die Tangente in diesem Punkt.
Leite die Funktion zum Schaubild ab und setzte den x-Wert des Punktes in die Ableitungsfunktion ein. Wir erhalten die Tangentensteigung.
Durch Verschiebung der entsprechenden Ursprungsgerade in x- und y-Richtung erhalten wir die Tangentengleichung:
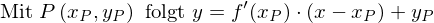
Durch Verschiebung der entsprechenden Ursprungsgerade in x- und y-Richtung erhalten wir die Tangentengleichung:
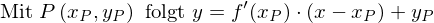
Tags: Tangente, Verschiebung
Quelle:
Quelle:
Wie löst man das folgende Tangentenproblem (Typ 2):
Eine Tangentensteigung ist gegeben. Gesucht ist/sind die Tangente(n) an das Schaubild mit dieser Steigung.
Eine Tangentensteigung ist gegeben. Gesucht ist/sind die Tangente(n) an das Schaubild mit dieser Steigung.
Leite die Funktion zum Schaubild ab und setzte die Ableitungsfunktion mit der gegebenen Steigung gleich. Die Gleichung besitzt eine oder mehrere Lösungen, je nachdem, ob es eine oder mehrere Tangenten mit der geforderten Steigung gibt.
Jede Lösung entspricht dem x-Wert eines Berührpunktes. Den zugehörigen y-Wert erhält man durch Einsetzen des x-Wertes in f(x).
Durch Verschiebung der Ursprungsgeraden mit der geforderten Steigung in x- und y-Richtung erhalten wir die Tangentengleichung:
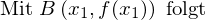
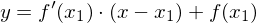
Bemerkungen:
Beim Schaubild der Kehrwertfunktion gibt es für alle Steigungen außer m=0 zwei Tangenten.
Bei Parabeln gerader Ordnung gibt es zu jeder Steigung genau eine Lösung.
Bei ganzrationalen Funktionen mit einem Grad > 2 kann es mehrere Lösungen geben.
Jede Lösung entspricht dem x-Wert eines Berührpunktes. Den zugehörigen y-Wert erhält man durch Einsetzen des x-Wertes in f(x).
Durch Verschiebung der Ursprungsgeraden mit der geforderten Steigung in x- und y-Richtung erhalten wir die Tangentengleichung:
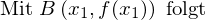
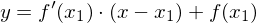
Bemerkungen:
Beim Schaubild der Kehrwertfunktion gibt es für alle Steigungen außer m=0 zwei Tangenten.
Bei Parabeln gerader Ordnung gibt es zu jeder Steigung genau eine Lösung.
Bei ganzrationalen Funktionen mit einem Grad > 2 kann es mehrere Lösungen geben.
Tags: ganzrational, Tangente, Verschiebung
Quelle:
Quelle:
Wie löst man das folgende Tangentenproblem (Typ 3):
Ein Punkt P außerhalb des Schaubildes ist gegeben. Gesucht ist/sind die Tangente(n) an das Schaubild durch diesen Punkt.
Ein Punkt P außerhalb des Schaubildes ist gegeben. Gesucht ist/sind die Tangente(n) an das Schaubild durch diesen Punkt.
Diesen Typ löst man mit einem zunächst variablen Berührpunkt oder alternativ mit einer Funktionenschar.
Der x-Wert des variablen Berührpunktes bzw. der Parameter der Funktionenschar werden mit Hilfe einer Gleichung so gewählt, dass die Tangente durch P verläuft.
siehe Lösungsvarianten bei Tangentenproblem 2 auf Tangentenprobleme in der Oberstufe
Der x-Wert des variablen Berührpunktes bzw. der Parameter der Funktionenschar werden mit Hilfe einer Gleichung so gewählt, dass die Tangente durch P verläuft.
siehe Lösungsvarianten bei Tangentenproblem 2 auf Tangentenprobleme in der Oberstufe
Tags: Tangente
Quelle:
Quelle:
Kartensatzinfo:
Autor: www.mathematik-bw.de
Oberthema: Mathematik
Thema: 10. Klasse
Schule / Uni: Clara-Schumann-Gymnasium
Ort: Lahr
Veröffentlicht: 23.12.2009
Schlagwörter Karten:
Alle Karten (47)
Ableitung (10)
Änderungsrate (9)
Anwendung (2)
Begriffe (17)
Definitionsmenge (1)
Extremstelle (2)
Funktion (8)
ganzrational (5)
Gerade (13)
Grad (1)
h-Methode (6)
hinreichend (3)
Intervalle (1)
Normale (2)
notwendig (2)
Nullstelle (5)
Produktform (3)
Sattelpunkt (3)
Schnittwinkel (1)
Sekante (1)
Sekantensteigung (1)
Steigungswinkel (3)
Streckung (1)
Symmetrie (3)
Tangente (7)
Terassenpunkt (3)
Verschiebung (7)
Wertemenge (1)



