Was ist Rechnersehen? Welche Probleme treten auf? Wofür braucht man die Epipolargeometrie in diesem Zusammenhang?
Wir wollen hier, anders als bei der CG, vom 2D Bild in die 3D Szene bzw. die 3D-Szene aus 2D-Bildern rekonstruieren.
Bsp.: Problem: Gegeben sei ein Roboter mit zwei Kameras (einem Stereokamerasystem). Der Roboter soll einen Anfahrtsweg zu einem Objekt berechnen können und das Objekt dann mittels Greifarm greifen können. Für diese Operationen brauchen wir die 3D-Rekonstruktion der gegebenen Szene. Eine Kamera liefert uns nur 2D-Informationen, die Tiefenwerte gehen aufgrund der Porjektion verloren.
Um die Tiefenwerte zu rekonstruieren brauchen wir mindestens Bilder aus zwei unterschiedlichen Positionen, die ca. den gleichen Bereich abdecken, um aufgrund dieser Informationen die Tiefenwerte zu rekonstruieren und so die Positionen im 3D-Raum im Bezug zum Roboter (in der Welt) bestimmen zu könnnen.
Letztendlich möchte man ausgehend von zwei Pixelkorrespondenzen der zwei Kameras den korrespondierenden Weltpunkt bestimmen.
Dabei gilt es zwei Probleme zu lösen:
- das Korrespondenzproblem
- das Rekonstruktionsproblem
Die Epipolargeometrie bietet uns die nötige Mathematik um die genannten Probleme zu lösen und die Gegebenheiten in Beziehung zu setzen.
Bsp.: Problem: Gegeben sei ein Roboter mit zwei Kameras (einem Stereokamerasystem). Der Roboter soll einen Anfahrtsweg zu einem Objekt berechnen können und das Objekt dann mittels Greifarm greifen können. Für diese Operationen brauchen wir die 3D-Rekonstruktion der gegebenen Szene. Eine Kamera liefert uns nur 2D-Informationen, die Tiefenwerte gehen aufgrund der Porjektion verloren.
Um die Tiefenwerte zu rekonstruieren brauchen wir mindestens Bilder aus zwei unterschiedlichen Positionen, die ca. den gleichen Bereich abdecken, um aufgrund dieser Informationen die Tiefenwerte zu rekonstruieren und so die Positionen im 3D-Raum im Bezug zum Roboter (in der Welt) bestimmen zu könnnen.
Letztendlich möchte man ausgehend von zwei Pixelkorrespondenzen der zwei Kameras den korrespondierenden Weltpunkt bestimmen.
Dabei gilt es zwei Probleme zu lösen:
- das Korrespondenzproblem
- das Rekonstruktionsproblem
Die Epipolargeometrie bietet uns die nötige Mathematik um die genannten Probleme zu lösen und die Gegebenheiten in Beziehung zu setzen.
Was ist das Korrespondenzproblem?

Im wesentlichen geht es darum in den beiden (Stereosystem) Pixelkoordinatensystemen korrespondierende Punkte zu finden. Das bedeutet, dass diese beiden Pixel ein und dem selben Punkt in der Welt repräsentieren.
Dies ist notwendig, da ansonsten der gesuchte zweite Punkt
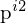 auf dem gesamten Sehstrahl
auf dem gesamten Sehstrahl 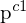 der ersten Kamera liegen könnte.
der ersten Kamera liegen könnte.Theoretisch kann der korrespondierende Punkt im gesamten zweiten Pixelkoordinatensystem liegen (sofern er überhaupt zu sehen ist).
Ist die Geometrie der Kameras gegeben, kann anhand der Epipolarbedingung das Korrespondenzproblem auf einen Suchraum von 2D -> 1D (die Epipolarlinie) reduziert werden.
Durch entsprechende Eigenschaften der Pixel kann dann die genaue Position im Pixelkoordinatensystem bestimmt werden:
- Punktdetektoren (Harris,Moravec), Features (SIFT, SURF,..), Kanten, ...
Wie kann man das/die Korrespondenzproblem/analyse vereinfachen?
1. nur Punkte, die in beiden Kameras zu sehen sind werden verwendet =>
links-rechts-Bedingung
2. Ist die Kamerageometrie bekannt (Kameraparameter gegeben oder geschätzte Werte), kann man den Suchbereich für einen Punkt auf eine Gerade im anderen Bild beschränken => Epipolarbedingung
links-rechts-Bedingung
2. Ist die Kamerageometrie bekannt (Kameraparameter gegeben oder geschätzte Werte), kann man den Suchbereich für einen Punkt auf eine Gerade im anderen Bild beschränken => Epipolarbedingung
Was ist das Rekonstruktionsproblem?

Sind die Geometrie des (Stereo-)Kamerasystems sowie die Korrespondenzen gegeben stellt sich die Frage, was man über die Position eines betrachteten Objektes in der Welt sagen kann (3D-Rekonstruktion). Bei diesem Problem geht es im wesentlichen darum die Tiefenwerte zu Rekonstruieren.
Dies geschieht mit Hilfe korrespondierender Punkte und deren Disparität (Versatz) der Pixelkoordinaten sowie dem Strahlensatz/Stereo-Triangulierung (siehe Zeichnung). Die Bilder können dabei in ideale Stereobilder (achsenparallel) überführt werden.
Dann vereinfacht sich die Berechnung wie folgt:
d(isparität) = x1-x2 (in
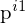 bzw.
bzw. 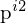 )
)Z = Tiefenwert des Weltpunktes
F = Brennweite
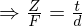
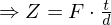
Was ist die Epipolargeometrie?
Die Epipolargeometrie befasst sich mit der Geometrie einer Szene, die von mindestens zwei Kameras gleichzeitig aufgenommen wird. Dies wird algebraisch mit der Essential Matrix (E-Matrix, extrinsische Kamerparameter) und der Fundamental Matrix (F-Matrix, extrinsische + intrinsische Kameraparameter) modelliert wird.
Die Punkte der Szene kommen größtenteils in den Bildern beider Kameras vor (Annahme). Diese Informationen können genutzt werden, um die Szene in 3D zu rekonstruieren.
Die Epipolargeometrie stellt eine Beziehung zwischen Bild-/Pixelkoordinaten korrespondierender Punkte her.
Die Punkte der Szene kommen größtenteils in den Bildern beider Kameras vor (Annahme). Diese Informationen können genutzt werden, um die Szene in 3D zu rekonstruieren.
Die Epipolargeometrie stellt eine Beziehung zwischen Bild-/Pixelkoordinaten korrespondierender Punkte her.
Was besagt die Epipolarbedingung?
Die Epipolarbedingung besagt, dass es eine eindeutige Abbildung gibt, die zu einem Punkt in Kamerabild 1 eine Linie (die Epipolarline) in Kamerabild 2 bestimmt auf der sich der korrespondierende Weltpunkt befindet.
Die Epipolarlinie entspricht dem projezierten Sehstrahl (in Kamerakoordinaten
) (vom optischen Zentrum auf den gesuchten Weltpunkt
(vom optischen Zentrum auf den gesuchten Weltpunkt  ) in das zweite Kamerabild (
) in das zweite Kamerabild (  ).
).
Die Epipolarlinie entspricht dem projezierten Sehstrahl (in Kamerakoordinaten
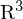
)
 (vom optischen Zentrum auf den gesuchten Weltpunkt
(vom optischen Zentrum auf den gesuchten Weltpunkt 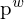 ) in das zweite Kamerabild (
) in das zweite Kamerabild (  ).
).Leiten Sie die Epipolarbedingung her.
(Herleitung der E-Matrix)
Mit Translation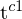 und Rotation
und Rotation 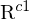 wird
wird  in
in 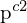 überführt (Kam1 in Kam2)
überführt (Kam1 in Kam2)
1.
2.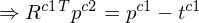
Koplanaritätsbedingung ( auf einer Ebene (Epipolarebene)).
auf einer Ebene (Epipolarebene)). 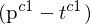 ist deshalb orthogonal zur Normale
ist deshalb orthogonal zur Normale 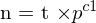 der Epipolarebene.
der Epipolarebene.
Dies kann durch das Skalarprodukt (entspricht Matrixmultiplikation mit Vektoren (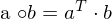 ) ausgedrückt werden:
) ausgedrückt werden:
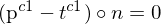 => Die Normale definiert die Epipolarebene.
=> Die Normale definiert die Epipolarebene.
3.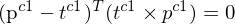
Dadurch werden alle Vektoren in Bezug zueinander gebracht und es wird bewiesen, dass sich alle (3) Vektoren in einer Ebene befinden.
4. Substitution: 2. in 3.
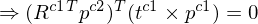
5. Kreuzprodukt als Kreuzproduktmatrix: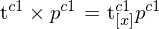
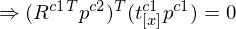
6. Anwendung Matrix-Arithmetrik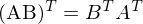
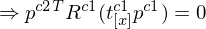
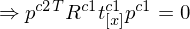
7. Substitution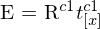
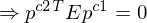
8. Perspektivische Projektion
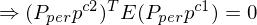
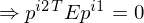
9. wir befinden uns nun in Bildkoordinaten ...das Kreuzprodukt zwischen zwei Punkten in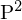 ergibt eine Linie (Projektive Linie (die Epipolarlinie)) => der Schnitt der Bildebene mit der Epipolarebene
ergibt eine Linie (Projektive Linie (die Epipolarlinie)) => der Schnitt der Bildebene mit der Epipolarebene
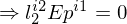
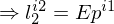
und
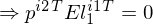
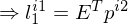
Mit Translation
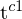 und Rotation
und Rotation 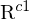 wird
wird  in
in 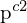 überführt (Kam1 in Kam2)
überführt (Kam1 in Kam2)1.

2.
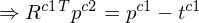
Koplanaritätsbedingung (
 auf einer Ebene (Epipolarebene)).
auf einer Ebene (Epipolarebene)). 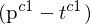 ist deshalb orthogonal zur Normale
ist deshalb orthogonal zur Normale 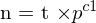 der Epipolarebene.
der Epipolarebene.Dies kann durch das Skalarprodukt (entspricht Matrixmultiplikation mit Vektoren (
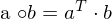 ) ausgedrückt werden:
) ausgedrückt werden: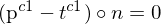 => Die Normale definiert die Epipolarebene.
=> Die Normale definiert die Epipolarebene. 3.
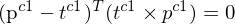
Dadurch werden alle Vektoren in Bezug zueinander gebracht und es wird bewiesen, dass sich alle (3) Vektoren in einer Ebene befinden.
4. Substitution: 2. in 3.
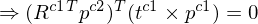
5. Kreuzprodukt als Kreuzproduktmatrix:
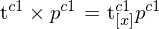
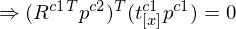
6. Anwendung Matrix-Arithmetrik
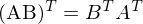
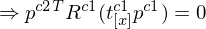
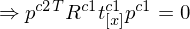
7. Substitution
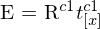
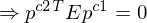
8. Perspektivische Projektion
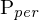
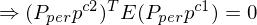
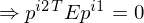
9. wir befinden uns nun in Bildkoordinaten ...das Kreuzprodukt zwischen zwei Punkten in
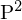 ergibt eine Linie (Projektive Linie (die Epipolarlinie)) => der Schnitt der Bildebene mit der Epipolarebene
ergibt eine Linie (Projektive Linie (die Epipolarlinie)) => der Schnitt der Bildebene mit der Epipolarebene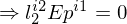
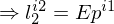
und
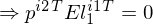
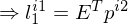
Wie kann man aus der Epipolarbedingung die Epipolarlinie herleiten?
E-Matrix = 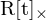
Cx = Kamerakoordinatensytem
Epipolarbedingung (Bildkoordinaten):
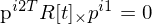
Ziel: Epipolarlinie in aus Punkt
aus Punkt 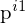 herleiten.
herleiten.
1.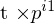 Koordinaten der
Koordinaten der 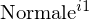 der Epipolarebene aus Sicht
der Epipolarebene aus Sicht 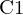 (projeziert in Bildkoordinaten
(projeziert in Bildkoordinaten 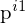 in
in 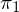 )
)
2.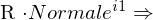
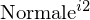 aus Sicht der
aus Sicht der 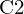 (projeziert in Bildkoordinaten,
(projeziert in Bildkoordinaten,  ) .
) .
3. (Substitution)
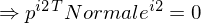
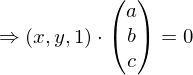
4. Homogene Gradengleichung (in 2D)
 Epipolarlinie
Epipolarlinie 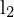
5. Auflösen nach y
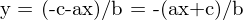
6. Zeichnen der Linie in : Für alle x-Werte (z.B. Breite der Bildebene) y-Werte berechnen
: Für alle x-Werte (z.B. Breite der Bildebene) y-Werte berechnen
=> Zu Punkt aus
aus 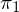 korrespondierende Koordinatenpaare für Epipolarlinie
korrespondierende Koordinatenpaare für Epipolarlinie 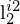 in
in  .
.
=>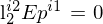
=>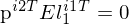
In Weltkoordinaten existiert eine Normale der Epipolarebene. Ziel ist es den Schnitt der Epipolarebene mit den Bildebenen in Bildkoordinaten oder direkt Pixelkoordinaten (mit Hilfe der F-Matrix) zu bestimmen.
Dieser Schnitt definiert die Epipolarline in den jeweiligen Pixelkoordinaten. Der Schnitt wird letztendlich also durch die Normale der Epipolarebene bestimmt. Die Koordinaten der Normale (in Weltkoordinaten eindeutig definiert) muss hierfür in die jeweiligen Koordinatensysteme der einzelnen Kameras bzw. deren Bildkoordinaten umgerechnet werden (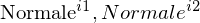 ), um die Epipolarlinie in diesen Koordinatensystemen zu bestimmen.
), um die Epipolarlinie in diesen Koordinatensystemen zu bestimmen.
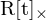
Cx = Kamerakoordinatensytem
Epipolarbedingung (Bildkoordinaten):
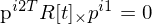
Ziel: Epipolarlinie in
 aus Punkt
aus Punkt 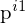 herleiten.
herleiten.1.
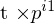 Koordinaten der
Koordinaten der 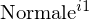 der Epipolarebene aus Sicht
der Epipolarebene aus Sicht 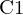 (projeziert in Bildkoordinaten
(projeziert in Bildkoordinaten 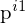 in
in 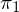 )
)2.
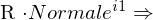
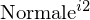 aus Sicht der
aus Sicht der 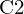 (projeziert in Bildkoordinaten,
(projeziert in Bildkoordinaten,  ) .
) .3. (Substitution)
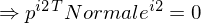
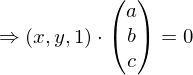
4. Homogene Gradengleichung (in 2D)
 Epipolarlinie
Epipolarlinie 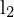
5. Auflösen nach y
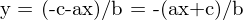
6. Zeichnen der Linie in
 : Für alle x-Werte (z.B. Breite der Bildebene) y-Werte berechnen
: Für alle x-Werte (z.B. Breite der Bildebene) y-Werte berechnen => Zu Punkt
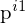 aus
aus 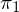 korrespondierende Koordinatenpaare für Epipolarlinie
korrespondierende Koordinatenpaare für Epipolarlinie 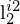 in
in  .
.=>
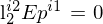
=>
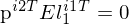
In Weltkoordinaten existiert eine Normale der Epipolarebene. Ziel ist es den Schnitt der Epipolarebene mit den Bildebenen in Bildkoordinaten oder direkt Pixelkoordinaten (mit Hilfe der F-Matrix) zu bestimmen.
Dieser Schnitt definiert die Epipolarline in den jeweiligen Pixelkoordinaten. Der Schnitt wird letztendlich also durch die Normale der Epipolarebene bestimmt. Die Koordinaten der Normale (in Weltkoordinaten eindeutig definiert) muss hierfür in die jeweiligen Koordinatensysteme der einzelnen Kameras bzw. deren Bildkoordinaten umgerechnet werden (
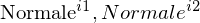 ), um die Epipolarlinie in diesen Koordinatensystemen zu bestimmen.
), um die Epipolarlinie in diesen Koordinatensystemen zu bestimmen. Welche Eigenschaften hat die E-Matrix?
- die E-Matrix ermöglicht die Abbildung zwischen Punkten (im Bildkoordinatensystem) der einen Kamera auf eine Linie (die Epipolarlinie, im Bildkoordinatensystem) der anderen Kamera
- sie enthält die extrinsischen Kameraparameter (R und t)
-

- Nullraum von E ist Vektor t (Translation der Kamera) => liegt ein Punkt auf Epipol selbst ist keine Berechnung möglich (Kreuzprodukt von zwei Vektoren gleicher Richtung = 0 (e = t =>
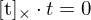 )
) - Multiplikation der E-Matrix mit Konstanten ändert epipolare Bedingung nicht
- E = Produkt aus R (Rang 3) und Kreuzproduktmatrix (Rang2) => e hat Rang 2!
- E hat 5 Freiheitsgrade: Rotation (3) u. Translation(3) => 6 - unbekannten Skalierungsfaktor (aufgrund Normalisierung) (1)
- zwei Singulärwerte sind gleich, der dritte ist 0
- det(E) = 0 // wegen Rang 2 der Kreuzproduktmatrix
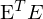 hängt nur von t ab:
hängt nur von t ab: 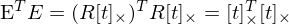
Leiten Sie die F-Matrix aus K- und E-Matrix her.
Im Gegensatz zur E-Matrix bezieht sich die F-Matrix nicht mehr auf Punkte in Bildkoordinaten, sondern erweitert die E-Matrix durch die intrinsischen Kameraparameter und bezieht sich deshalb direkt auf Pixelkoordinaten.
Annahme: intrinsische Kameraparameter sind bekannt.
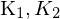
1.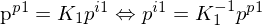
2.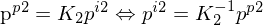
3. Einsetzen in Epipolarbedingung
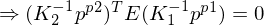
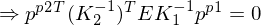
4. F-Matrix =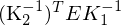
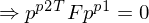
Die Matrix bildet einen Punkt (in Pixelkoordinaten) der einen Kamera auf die epipolare Linie in Pixelkoordinaten der zweiten Kamera ab.
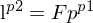
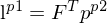
Die F-Matrix kann auch ohne Vorwissen über Geometrie oder Parameter geschätzt werden => siehe 8-Punkte-Algorithmus
Annahme: intrinsische Kameraparameter sind bekannt.
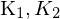
1.
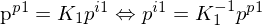
2.
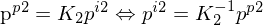
3. Einsetzen in Epipolarbedingung

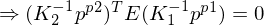
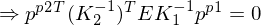
4. F-Matrix =
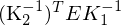
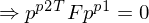
Die Matrix bildet einen Punkt (in Pixelkoordinaten) der einen Kamera auf die epipolare Linie in Pixelkoordinaten der zweiten Kamera ab.
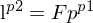
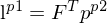
Die F-Matrix kann auch ohne Vorwissen über Geometrie oder Parameter geschätzt werden => siehe 8-Punkte-Algorithmus
Erklären Sie die Gleichung für die Epipolarbedingung.
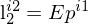
Die eigentliche Linie
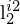 , darf hierbei nicht einfach als Vektor interpretiert werden, sondern ist die Umsetzung der Geradengleichung ax+by+c=0. Die Parameter a,b und c
, darf hierbei nicht einfach als Vektor interpretiert werden, sondern ist die Umsetzung der Geradengleichung ax+by+c=0. Die Parameter a,b und csind die Komponenten des Vektors von
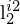 .
.Geometrisch stellt
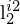 die Normale (die Normale bestimmt den Schnitt der beiden Ebenen) auf der Epipolarebene aus Sicht von Kamera 2 dar. Sie lässt sich herleiten aus der Schnittgeraden von der Bildebene des zweiten Kamerasystems und der Epipolarebene.
die Normale (die Normale bestimmt den Schnitt der beiden Ebenen) auf der Epipolarebene aus Sicht von Kamera 2 dar. Sie lässt sich herleiten aus der Schnittgeraden von der Bildebene des zweiten Kamerasystems und der Epipolarebene.(ansonsten wie bei E-Matrix)
Was macht die F-Matrix?
Die F(undamental)-Matrix beihnaltet die Informationen der intrinsischen und extrinsischen Kameraparameter und kann somit zur Abbildung von Punkten des einem Pixelkoordinatensystems in die entsprechende Epipolarlinie des anderes Pixelkoordinatensystems genutzt werden (Punkt => Linie).
Welche Eigenschaften hat die F-Matrix?
- F hat 7 Freiheitsgrade (5 aus E-Matrix + 2 aus Skalierung der K-Matrizen)
-
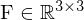
- als Produkt aus
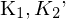 ' (voller Rang) u. E-Matrix (Rang 2) => F hat Rang 2
' (voller Rang) u. E-Matrix (Rang 2) => F hat Rang 2 - det(F) = 0
- F ist nur eindeutig bis auf einen Skalierungsfaktor
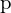 mit ||F|| = 1
mit ||F|| = 1 - F-Matrix kann durch Punktkorrespondenzen geschätzt werden (z.B. im Zusammenhang der Kalibrierung) => danach steht F-Matrix zur Verfügung und kann zur weiteren Korrespondenzfindung im Einsatz (z.B. des Roboters) genutzt werden
Welche Eigenschaften hat eine Rotationsmatrix?
-
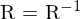 für Rotation mit Winkel 0 und
für Rotation mit Winkel 0 und 
-
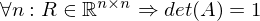 , Determinante hat immer Wert 1 => ist invertierbar und verändert Volumen nicht => voller Rang!
, Determinante hat immer Wert 1 => ist invertierbar und verändert Volumen nicht => voller Rang! -
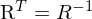
- von den drei Eigentwerten einer Rotationsmatrix ist einer reell und hat den Wert 1 => korrespondiert zur Rotationsachse
- Rang(R) = 3, Rotationsmatrizen haben immer den vollen Rang!
Was sind die Ausgabeparameter der Singulärwertzerlegung (SVD)? ... Wie lassen sie sich interpretieren?
Sie ist eine Normalform für Matrizen und zerlegt eine Matrix 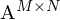 in 3 einzelne Matrizen mit jeweils speziellen Eigenschaften. Es können die Singulärwerte der Matrix abgelsen werden.
in 3 einzelne Matrizen mit jeweils speziellen Eigenschaften. Es können die Singulärwerte der Matrix abgelsen werden.
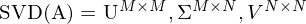
A wieder aus 3 Matrizen zurückrechnen:
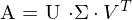
Die Matrix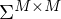 :
:
Enthält auf der Diagonalen, positive, nach der Größe sortierte Singulärwerte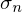 .
.
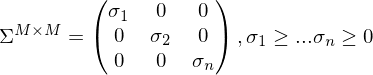
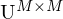 :
:
Die Singulärwerte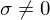 korrespondierenden Spaltenvektoren
korrespondierenden Spaltenvektoren 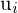 der Matrix U sind die Basisvektoren des Bildraumes.
der Matrix U sind die Basisvektoren des Bildraumes.
Die Spaltenvektoren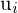 sind die Eigenvektoren von
sind die Eigenvektoren von 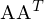 (bei
(bei  => Zeilenvektoren)
=> Zeilenvektoren)
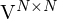 :
:
Die zu den Singulärwerten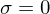 korrespondierenden Spaltenvektoren
korrespondierenden Spaltenvektoren 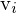 sind die Basisvektoren des Nullraums. Die Spaltenvektoren sind ebenfalls orthonormal. (bei
sind die Basisvektoren des Nullraums. Die Spaltenvektoren sind ebenfalls orthonormal. (bei 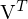 => Zeilenvektoren)
=> Zeilenvektoren)

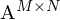 in 3 einzelne Matrizen mit jeweils speziellen Eigenschaften. Es können die Singulärwerte der Matrix abgelsen werden.
in 3 einzelne Matrizen mit jeweils speziellen Eigenschaften. Es können die Singulärwerte der Matrix abgelsen werden.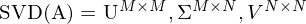
A wieder aus 3 Matrizen zurückrechnen:
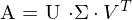
Die Matrix
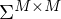 :
:Enthält auf der Diagonalen, positive, nach der Größe sortierte Singulärwerte
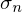 .
.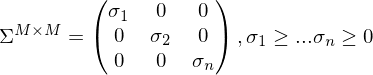
- Rang(A) = Anzahl Singulärwerte
 0
0 - Dimension des Nullraums (Kern) entspricht Anzahl
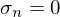
- Singulärwerte sind die Quadratwurzeln der Eigenwerte von
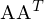
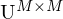 :
:Die Singulärwerte
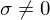 korrespondierenden Spaltenvektoren
korrespondierenden Spaltenvektoren 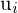 der Matrix U sind die Basisvektoren des Bildraumes.
der Matrix U sind die Basisvektoren des Bildraumes.Die Spaltenvektoren
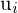 sind die Eigenvektoren von
sind die Eigenvektoren von 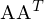 (bei
(bei  => Zeilenvektoren)
=> Zeilenvektoren)-
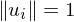
- '
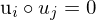
- => sind orthonormal
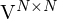 :
:Die zu den Singulärwerten
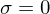 korrespondierenden Spaltenvektoren
korrespondierenden Spaltenvektoren 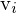 sind die Basisvektoren des Nullraums. Die Spaltenvektoren sind ebenfalls orthonormal. (bei
sind die Basisvektoren des Nullraums. Die Spaltenvektoren sind ebenfalls orthonormal. (bei 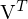 => Zeilenvektoren)
=> Zeilenvektoren)
- Beispiel SVD einer Scherung
-
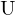 und
und 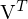 können als Rotationsmatrizen interpretiert werden
können als Rotationsmatrizen interpretiert werden -
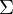 als Skalierungsmatrix um die Faktoren
als Skalierungsmatrix um die Faktoren 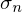
Was sind die Anwendungen der SVD? Welche kennen Sie?
- Man kann den Nullraum einer Matrix bestimmen (Bsp.: 8-Punkte-Algorithmus)
- Man kann die Pseudoinverse
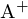 einer Matrix
einer Matrix 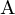 bestimmen (
bestimmen ( ,
,  enthält Kehrwerte der ursprünglichen Singulärwerte, wobei die Werte gleich 0 bestehen bleiben
enthält Kehrwerte der ursprünglichen Singulärwerte, wobei die Werte gleich 0 bestehen bleiben - Rang einer Matrix erzwingen (Singulärewerte ungleich 0 von unten nach oben durch 0 ersetzen, Bsp.: 8-Punkte-Algorithmus)
- Orthogonalisierung einer Matrix (
 durch Einheitsmatrix
durch Einheitsmatrix 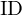 ersetzen)
ersetzen) - Lösen von Linearen Gleichungssystemen (LGS) durch Berechnen des Nullraumes (Bsp.: 8-Punkte-Algorithmus)
Ich gebe Ihnen zwei Fotos. Wie funktioniert damit der 8 Punkte Algorithmus? bzw. Wie kann man die F-Matrix schätzen?
1. mindestens 8 linear unabhängige (nicht auf einer Linie liegende) Punktkorrespondezen in beiden Bildern finden
2. F-Matrix mit Hilfe des 8-Punkte-Algorithmus schätzen
Jedes Punktepaar / jede Punktkorrespondenz liefert eine Gleichung der Form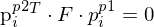 , mit
, mit 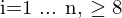
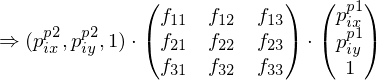
... Umformen bis alles in einer Zeile steht (siehe Skript Ameling) .
Dann f-Werte aus Gleichungen herausnehmen und in LGS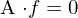 umformen.
umformen.
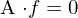
Somit ist f der Nullraum von A und kann mittels SVD bestimmt werden.
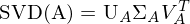
Durch Rauschen kann A auch einen Rang größer 8, also 9 haben. Der Nullraum ergibt sich aus der Spalte von V korrespondierend zum kleinsten Singulärewert von A. Dabei ist F nur bis auf einen Skalierungsfaktor eindeutig.
eindeutig.

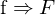
Es muss sichergestellt werden, dass F den Rang zwei hat (Eigenschaft der beinhalteten E-Matrix). Der Rang kann durch die SVD erzwungen werden.
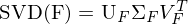
Nun wird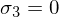 gesetzt und die F-Matrix neu berechnet:
gesetzt und die F-Matrix neu berechnet:
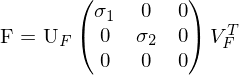
Der Algorithmus ist numerisch instabil. Zur Stabilisierung können die Koordinaten normalisiert werden, so dass die Einträge von A in einer vergleichbaren Größe stabil sind.
- kann manuell geschehen oder
- durch Merkmalsdetektion (Gradienten, Ecken, Features, ...)
2. F-Matrix mit Hilfe des 8-Punkte-Algorithmus schätzen
- F-Matrix kann bis auf einen Skalierungsfaktor
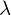 eindeutig bestimmt werden (dieser Skalierungsfaktor bestimmt das eigentliche Größenverhältnis (z.B. wieviel Millimeter entsprechen einem Pixel) ... wid in Kalibrierung/Kameramodell bestimmt
eindeutig bestimmt werden (dieser Skalierungsfaktor bestimmt das eigentliche Größenverhältnis (z.B. wieviel Millimeter entsprechen einem Pixel) ... wid in Kalibrierung/Kameramodell bestimmt - je mehr Punktkorrespondenzen
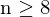 zur Verfügung stehen, desto stabiler wird das Ergebnis
zur Verfügung stehen, desto stabiler wird das Ergebnis
Jedes Punktepaar / jede Punktkorrespondenz liefert eine Gleichung der Form
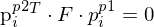 , mit
, mit 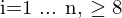
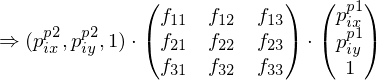
... Umformen bis alles in einer Zeile steht (siehe Skript Ameling) .
Dann f-Werte aus Gleichungen herausnehmen und in LGS
 umformen.
umformen. - für jede Punktkorrespondenz entsteht eine Zeile in A
- Anzahl der Spalten von A ist 9 (Werte der F-Matrix)
- die 9 Werte der F-Matrix stehen im Spaltenvektor f
Somit ist f der Nullraum von A und kann mittels SVD bestimmt werden.
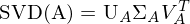
Durch Rauschen kann A auch einen Rang größer 8, also 9 haben. Der Nullraum ergibt sich aus der Spalte von V korrespondierend zum kleinsten Singulärewert von A. Dabei ist F nur bis auf einen Skalierungsfaktor
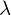 eindeutig.
eindeutig.
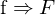
Es muss sichergestellt werden, dass F den Rang zwei hat (Eigenschaft der beinhalteten E-Matrix). Der Rang kann durch die SVD erzwungen werden.
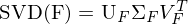
Nun wird
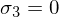 gesetzt und die F-Matrix neu berechnet:
gesetzt und die F-Matrix neu berechnet: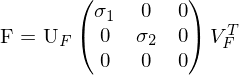
Der Algorithmus ist numerisch instabil. Zur Stabilisierung können die Koordinaten normalisiert werden, so dass die Einträge von A in einer vergleichbaren Größe stabil sind.
Wo stehen die Lösungswerte für F denn ganz genau?
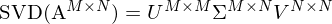
(Ausgabe in Octave)
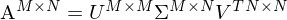
Die Werte stehen in der letzten Zeile von
 bzw. letzte Spalte von
bzw. letzte Spalte von 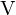 . Wollte mir Herr Müller nicht glauben, habs ihm damit erklärt dass die Matrixmultiplikation ja Zeile*Spalte läuft, der letzte Singulärwert steht ja am Ende der letzten Zeile von
. Wollte mir Herr Müller nicht glauben, habs ihm damit erklärt dass die Matrixmultiplikation ja Zeile*Spalte läuft, der letzte Singulärwert steht ja am Ende der letzten Zeile von  , also wird der immer mit dem letzten Element der entsprechenden Spalte von
, also wird der immer mit dem letzten Element der entsprechenden Spalte von 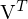 multipliziert, und das steht ja immer in der letzten Zeile von
multipliziert, und das steht ja immer in der letzten Zeile von 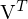 (rot) bzw. der letzten Spalte von
(rot) bzw. der letzten Spalte von 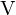 :
:
Braucht man immer 8 Punkte und wird es mit 12 Punkten besser?
Man braucht mindestens 8 Punkte (im Hartley steht, das man sogar nur 7 braucht ... dann aber uneindeutig Nullraum 2Dimensional), aber nicht genau 8. Mit 12 Punkten wird es besser, denn:
je mehr Punktkorrespondenzen vorhanden sind, desto genauer die Korrespondenzanalyse und Rekonstruktion.
Erklärung: Durch die Angabe der Korrepsondenzen in Pixeln wird die Welt diskretisiert ... was immer mit einem gewissen Fehler verbunden ist ... dieser Fehler geht in jede "Richtung" für jedes Pixel ... durch mehr Korrespondenzen werden einseitige Verzerrungen des Fehlers unwahrscheinlicher und das Ergbnis insgesamt stabiler ....
je mehr Punktkorrespondenzen vorhanden sind, desto genauer die Korrespondenzanalyse und Rekonstruktion.
Erklärung: Durch die Angabe der Korrepsondenzen in Pixeln wird die Welt diskretisiert ... was immer mit einem gewissen Fehler verbunden ist ... dieser Fehler geht in jede "Richtung" für jedes Pixel ... durch mehr Korrespondenzen werden einseitige Verzerrungen des Fehlers unwahrscheinlicher und das Ergbnis insgesamt stabiler ....
Wie funktioniert das RANSAC (Random Sampling Consensus) Verfahren und wofür braucht man es?

Ein Problem ist, dass Punktkorrespondenzen oft nicht exakt sind. Die Fehler bei Punktkorrespondenzen können in zwei Klassen unterteilt werden:
- Schlechte Lokalisierung der Punktkorrespondenzen
- Falsche Korrespondenzen
Während in klassischen Schätzverfahren die Gesamtheit aller Messungen entsprechend dem kleinsten quadratischen Fehler berücksichtig wird, und dies im Falle von Ausreißern sehr
instabil ist, geht der RANSAC Algorithmus den umgekehrten weg.
1. Wähle m zufällige Mengen aus den Punktkorrespondenzen aus, wobei jede Menge aus 7 Korrespondenzen besteht, da die F-Matrix 7 unabhängige Parameter besitzt.
2. Für jede dieser Mengen wird
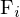 berechnet.
berechnet.3. Bestimme die Anzahl der Korrespondenzen, die mit
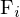 konsistent sind. Ergebnis: 2 Mengen (konsistente und nicht-konsistente Korrespondenzen). Konsistent bedeutet, dass der Fehler beim Anwenden von
konsistent sind. Ergebnis: 2 Mengen (konsistente und nicht-konsistente Korrespondenzen). Konsistent bedeutet, dass der Fehler beim Anwenden von 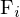 kleiner als ein bestimmter Schwellwert ist.
kleiner als ein bestimmter Schwellwert ist.Beispiel einer Iteration
1.
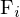 wurde aus einer der Mengen bestimmt
wurde aus einer der Mengen bestimmt2. wende nun
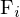 auf alle Punktkorrespondenzen an
auf alle Punktkorrespondenzen an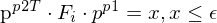
Durch die Epipolarbedingung wissen wir, dass bei einer korrekten F-Matrix mit korrekten Korrsepondenzen 0 herauskommen müsste ... in der Praxis nimmt man hier einen Schwellwert an.
Man behält letztendlich die Korrespondenzen, die mit einer
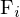 die meisten Werte unterhalb des Schwellwertes erfüllen => größte konsistente Menge an Korrespondenzen
die meisten Werte unterhalb des Schwellwertes erfüllen => größte konsistente Menge an Korrespondenzen4. Behalte die größte konsistente Menge von Korrespondenzen.
5. Ende:
F ein letztes mal mit dem 8-Punkte-Algorithmus berechnen. Alle konsistenten Punktkorrespondenzen benutzen
Was steht in der K-Matrix?
Die intrinsischen Parameter charackterisieren die Abbildung eines Bildpunktes von der Kamera zu Pixelkoordinaten.
Die K-Matrix modelliert die intrinsischen Kameraparamater (algebraisch).
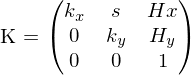
Skew,Versatz(Scheerung) des digitalen Chips, Die Achsen des CCD-Chips sind nicht orthogonal.
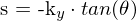
Skalierung, beihnaltet Projektion (Projektion wird nur zum Verständnis extra beschrieben, Bildebene existiert in Realität nicht)
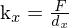 ,
, 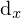 = Größe der Sensorelemente (x-Komponente)
= Größe der Sensorelemente (x-Komponente)
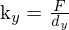 ,
, 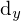 = Größe der Sensorelemente (y-Komponente)
= Größe der Sensorelemente (y-Komponente)
Hauptpunkt: Translation => von Ursprung (Bildkoordinaten) in Ursprung (Pixelkoordinaten) verschieben (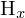 ,
,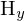 )
)
Die K-Matrix modelliert die intrinsischen Kameraparamater (algebraisch).
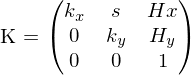
Skew,Versatz(Scheerung) des digitalen Chips, Die Achsen des CCD-Chips sind nicht orthogonal.
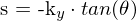
Skalierung, beihnaltet Projektion (Projektion wird nur zum Verständnis extra beschrieben, Bildebene existiert in Realität nicht)
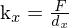 ,
, 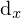 = Größe der Sensorelemente (x-Komponente)
= Größe der Sensorelemente (x-Komponente)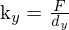 ,
, 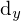 = Größe der Sensorelemente (y-Komponente)
= Größe der Sensorelemente (y-Komponente)Hauptpunkt: Translation => von Ursprung (Bildkoordinaten) in Ursprung (Pixelkoordinaten) verschieben (
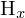 ,
,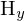 )
)- 5 Freiheitsgrade (Skalierung(2D)(2), Translation(2D)(2), Skew(1))
- Rang(K) = 3 (voller Rang)
Was sind die intrinsischen Kameraparametern? Was gehört dazu?
Beschreiben die optische, geometrischen und digitalen Eigenschaften einer Kamera. Dieses Parameter ändern sich nicht wenn die Kamera bewegt wird, sie sind aber von Kamera zu Kamera unterschiedlich.
H: Hauptpunkt: Ursprung des Bildkoordinatensystems. Stimmt normalerweise nicht mit dem Schnittpunkt der optischen Achse der Bildebene überein.
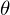 : Skew (Schräge) Winkel => die Achsen des CCD-Chips sind nicht orthogonal.
: Skew (Schräge) Winkel => die Achsen des CCD-Chips sind nicht orthogonal.
 : Größe der Sensorelemenete(Pixelgröße)
: Größe der Sensorelemenete(Pixelgröße)
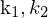 : Radiale Verzerrung
: Radiale Verzerrung
F : Brennweite
H: Hauptpunkt: Ursprung des Bildkoordinatensystems. Stimmt normalerweise nicht mit dem Schnittpunkt der optischen Achse der Bildebene überein.
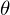 : Skew (Schräge) Winkel => die Achsen des CCD-Chips sind nicht orthogonal.
: Skew (Schräge) Winkel => die Achsen des CCD-Chips sind nicht orthogonal. : Größe der Sensorelemenete(Pixelgröße)
: Größe der Sensorelemenete(Pixelgröße)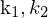 : Radiale Verzerrung
: Radiale VerzerrungF : Brennweite
Was sind die extrinsischen Kameraparameter?
Die extrinsischen (Kamera) - Parameter beschreiben die relative Position und Orientierung der Kameras in der Welt (Szene) und somit auch zueinander.
Es gitb eine regide Transformation bestehend aus Rotation und Translation, die jedes Kamerakoordinatensystem in das jeweilig andere überführen kann.
Es gitb eine regide Transformation bestehend aus Rotation und Translation, die jedes Kamerakoordinatensystem in das jeweilig andere überführen kann.
Erklären Sie umgangssprachlich, wie sich bei der Zerlegung der essentiellen Matrix E der Translationsvektor t berechnen lässt.
Für jeden Punkt in den Bildebenen lässt sich die zugehörige epipolare Linie bestimmen, die durch eben diesen Punkt und den jewiligen Epipol geht. Liegt der Punkt jedoch auf dem Vektor t, ist also der Epipol selbst, so ist keine Berechnung möglich (Kreuzprodukt von zwei Vektoren gleicher Richtung = 0, e = t => 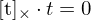 ).
).
Dieser Punkt liegt also um Nullraum von E. Bestimmt man den Nullraum von E (z.B. mittels SVD), so erhält man also gerade den Vektor t, allerdings skaliert um einen unbekannten Faktor.
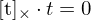 ).
).Dieser Punkt liegt also um Nullraum von E. Bestimmt man den Nullraum von E (z.B. mittels SVD), so erhält man also gerade den Vektor t, allerdings skaliert um einen unbekannten Faktor.
Kann man die Geometrie ohne Translation rekonstruieren?
Nein!
Die Rekonstruktion erfolgt durch die Stereo-Triangulierung bzw. Anwendung des Strahlensatzes auf idealisierte Stereobilder. Dabei ergeben sich folgende Verhältnisse (Bsp.: X-Koordinaten):
Z = Tiefenwert (gesucht), F = Brennweite, t = Translation zwischen Kameras,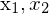 = Punktkorrespondenz, d = Disparität (Versatz)
= Punktkorrespondenz, d = Disparität (Versatz)
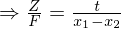
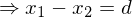
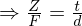
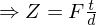
Wäre "t" = 0 wird der Bezug zu Dsiparität erbenfalls 0
=> der Z-Wert lässt sich nicht rekonstruieren.
Die Rekonstruktion erfolgt durch die Stereo-Triangulierung bzw. Anwendung des Strahlensatzes auf idealisierte Stereobilder. Dabei ergeben sich folgende Verhältnisse (Bsp.: X-Koordinaten):
Z = Tiefenwert (gesucht), F = Brennweite, t = Translation zwischen Kameras,
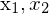 = Punktkorrespondenz, d = Disparität (Versatz)
= Punktkorrespondenz, d = Disparität (Versatz)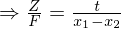
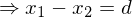
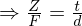
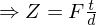
Wäre "t" = 0 wird der Bezug zu Dsiparität erbenfalls 0
=> der Z-Wert lässt sich nicht rekonstruieren.
Kann man Geometrie auch rekonstruieren, wenn man keine Rotation hat?
Ja!
Dies ist möglich bei einem Achsenparallelen Stereosystem ... dort gibt es keine relative Rotation zwischen beiden Kamerasystemen ... die Geometrie lässt sich direkt anhand der Disparität rekonstruieren.
(Es gibt vorgefertigte, "perfekt" zu einander ausgerichtete/kalibrierte Stereokamerasysteme (Bsp.: RoboCup)
Dies ist möglich bei einem Achsenparallelen Stereosystem ... dort gibt es keine relative Rotation zwischen beiden Kamerasystemen ... die Geometrie lässt sich direkt anhand der Disparität rekonstruieren.
(Es gibt vorgefertigte, "perfekt" zu einander ausgerichtete/kalibrierte Stereokamerasysteme (Bsp.: RoboCup)
Was ändert sich in der Epipolargeometrie im Achsenparallelen Fall?
Da die Bildebenen der Kameras parallel ausgerichtet sind verlaufen die Schnittgeraden der Epipolarebene mit der Bildebene, also die Epipolarlinien, alle parallel zueinander.
Die Basislinie schneidet die Bildebene im Unendlichen ... somit liegen auch die Epipole im Unendlichen.
Die Basislinie schneidet die Bildebene im Unendlichen ... somit liegen auch die Epipole im Unendlichen.
Was sind die Epipole? Welche Eigenschaften haben sie?
Annahme: Stereokamerasystem
- Der linke Epipol ist die Projektion des rechten optischen Zentrums (Projektionszentrums) und umgekehrt.
- Allgemein: Das Bild des Projekionszentrums einer Kamera in das Projektionszentrum der anderen wird Epipol genannt
- nur eine Epipolare Linie geht durch jeden Bildpunkt! => aber: jeder Epipolarlinie geht durch den Epipol der jeweiligen Kamera!
Wie berechnet man die Epipole aus der F-Matrix?
Da 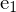 auf allen epipolaren Lienien im linken Kamerabild liegt folgt aus
auf allen epipolaren Lienien im linken Kamerabild liegt folgt aus
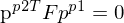
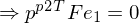
da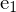 bei allen
bei allen 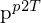 gleich ist und
gleich ist und 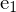 auf der Basislinie (t) liegt und sich damit auch im Nullraum von E und somit auch im Nullraum von F befindet
auf der Basislinie (t) liegt und sich damit auch im Nullraum von E und somit auch im Nullraum von F befindet
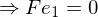
Der Epipol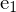 liegt also im Nullraum von
liegt also im Nullraum von 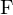 und folglich
und folglich 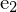 im Nullraum von
im Nullraum von 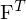 .
.
Durch folgenden Algorithmus lassen sich die Epipole geschickt aus F berechnen:
1. Berechne SVD(F) =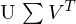
2.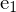 ist die Spalte von V korrespondierend zu
ist die Spalte von V korrespondierend zu 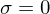
3.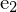 ist die Spalte von U korrespondierend zu
ist die Spalte von U korrespondierend zu 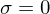
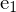 auf allen epipolaren Lienien im linken Kamerabild liegt folgt aus
auf allen epipolaren Lienien im linken Kamerabild liegt folgt aus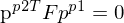
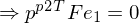
da
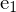 bei allen
bei allen 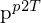 gleich ist und
gleich ist und 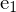 auf der Basislinie (t) liegt und sich damit auch im Nullraum von E und somit auch im Nullraum von F befindet
auf der Basislinie (t) liegt und sich damit auch im Nullraum von E und somit auch im Nullraum von F befindet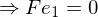
Der Epipol
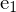 liegt also im Nullraum von
liegt also im Nullraum von 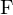 und folglich
und folglich 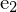 im Nullraum von
im Nullraum von 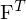 .
.Durch folgenden Algorithmus lassen sich die Epipole geschickt aus F berechnen:
1. Berechne SVD(F) =
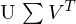
2.
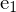 ist die Spalte von V korrespondierend zu
ist die Spalte von V korrespondierend zu 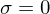
3.
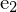 ist die Spalte von U korrespondierend zu
ist die Spalte von U korrespondierend zu 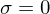
Wie kann man R und t berechnen, wenn F bekannt ist?
Ist die F-Matrix (z.B. aus 8-Punkte-Algorithmus) gegeben, kann man die Rotation und Translation der Kameras zueinander berechnen.
Voraussetzung: interne /intrinsische Kameraparameter sind bekannt!
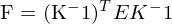
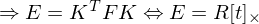
1. t lässt sich über Nullraum von E bestimmen (mittels SVD)
2. R minimieren der Norm
=> es entsteht ein nicht-lineares Optimierungsproblem!
=> unter Verwendung von Quaterionen kann es in ein lineares Problem konvertiert werden (siehe Skript Ameling für Beweis)
Voraussetzung: interne /intrinsische Kameraparameter sind bekannt!
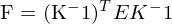
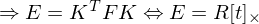
1. t lässt sich über Nullraum von E bestimmen (mittels SVD)
2. R minimieren der Norm

- Bedingung: det(R) = 1
- R ist eine orthogonale Matrix:

=> es entsteht ein nicht-lineares Optimierungsproblem!
=> unter Verwendung von Quaterionen kann es in ein lineares Problem konvertiert werden (siehe Skript Ameling für Beweis)
Warum lässt sich die Formel 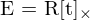 nicht nach R auflösen?
nicht nach R auflösen?
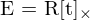 nicht nach R auflösen?
nicht nach R auflösen?Weil man dazu 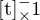 bilden müsste ( um
bilden müsste ( um 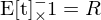 zu berechnen), da aber
zu berechnen), da aber 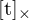 nicht invertierbar ist, da die Matrix nur Rang = 2 hat, anstatt wie erforderlich den vollen Rang 3 (bei 3x3 Matrix) hat. Im Kreuzprodukt geht also eine Dimension verloren, was ebenfalls bedeutet det(
nicht invertierbar ist, da die Matrix nur Rang = 2 hat, anstatt wie erforderlich den vollen Rang 3 (bei 3x3 Matrix) hat. Im Kreuzprodukt geht also eine Dimension verloren, was ebenfalls bedeutet det(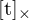 ) = 0.
) = 0.
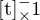 bilden müsste ( um
bilden müsste ( um 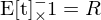 zu berechnen), da aber
zu berechnen), da aber 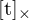 nicht invertierbar ist, da die Matrix nur Rang = 2 hat, anstatt wie erforderlich den vollen Rang 3 (bei 3x3 Matrix) hat. Im Kreuzprodukt geht also eine Dimension verloren, was ebenfalls bedeutet det(
nicht invertierbar ist, da die Matrix nur Rang = 2 hat, anstatt wie erforderlich den vollen Rang 3 (bei 3x3 Matrix) hat. Im Kreuzprodukt geht also eine Dimension verloren, was ebenfalls bedeutet det(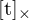 ) = 0.
) = 0.Steht die Normale, welche die epipolare Linie definiert, immer senkrecht in der Bildebene?
Nein, fast nie ... das wäre nur im Sonderfall gegeben, wenn Bildebene und die epipolare Ebene senkrecht aufeinander stehen.
Im perfekt achsenparallelen Fall (gleiche y- und x-Koordinaten) von zwei Kameras ist dies allerdings immer der Fall!
Im perfekt achsenparallelen Fall (gleiche y- und x-Koordinaten) von zwei Kameras ist dies allerdings immer der Fall!
Warum braucht/benutzt man überhaupt homogene Koordinaten?
"Für die Verknüfung durch Hintereinanderausführung ist es vorteilhaft, wenn alle Operationen jeweils als Matrixmultiplikation beschreibbar sind." (Burger 06, Digitale Bildverarbeitung)
In der Bildentstehungpipeline (Welt->Kamera->Bild->Pixel) verwenden wir Translationen (Vektoradditionen) und die Perspektivische Division.
Eine Vektoraddition kann erst durch die homogene Koordinate als Matrixoperation verwendet werden:
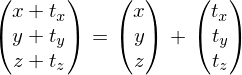
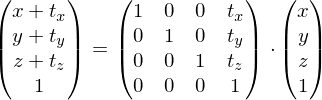
Die Perspektivische Division ist nicht linear und kann so auch nicht als Matrixoperation dargestellt werden. Erst durch die homogenen Koordinaten und die Homogenisierung kann sie aus den eigentlichen Matrixoperationen "ausgelagert" werden und in einem eigenen fest definierten Schritt (der Homogenisierung) nach Anwendung der Projektionsmatrix erfolgen:

Nach der Homogenisierung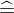 bleibt genau der Strahlensatz vom Lochkameramodell übrig.
bleibt genau der Strahlensatz vom Lochkameramodell übrig.
In der Bildentstehungpipeline (Welt->Kamera->Bild->Pixel) verwenden wir Translationen (Vektoradditionen) und die Perspektivische Division.
Eine Vektoraddition kann erst durch die homogene Koordinate als Matrixoperation verwendet werden:
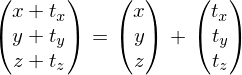
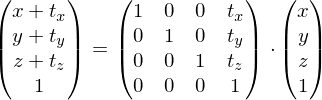
Die Perspektivische Division ist nicht linear und kann so auch nicht als Matrixoperation dargestellt werden. Erst durch die homogenen Koordinaten und die Homogenisierung kann sie aus den eigentlichen Matrixoperationen "ausgelagert" werden und in einem eigenen fest definierten Schritt (der Homogenisierung) nach Anwendung der Projektionsmatrix erfolgen:

Nach der Homogenisierung
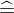 bleibt genau der Strahlensatz vom Lochkameramodell übrig.
bleibt genau der Strahlensatz vom Lochkameramodell übrig.Aus 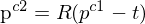 , daraus kann man ja
, daraus kann man ja 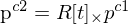 herleiten. Könnte man das auch als eine einzige 4x4 Matrix mit der 3x3 Rotation links oben und t in der letzten Spalte schreiben?
herleiten. Könnte man das auch als eine einzige 4x4 Matrix mit der 3x3 Rotation links oben und t in der letzten Spalte schreiben?
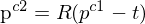 , daraus kann man ja
, daraus kann man ja 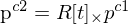 herleiten. Könnte man das auch als eine einzige 4x4 Matrix mit der 3x3 Rotation links oben und t in der letzten Spalte schreiben?
herleiten. Könnte man das auch als eine einzige 4x4 Matrix mit der 3x3 Rotation links oben und t in der letzten Spalte schreiben?Nein!
Wenn man die Matrizen R und [t]x miteinander multipliziert kommt eine Matrix von anderer Gestalt raus.
Außerdem wäre das Ergebnis der Multiplikation eines Punktes unterschiedlich (mit Octave geprüft).
Die Keuzproduktmatrix entspricht nicht einer Translation.
Außerdem ist es ein Unterschied, ob man erst transliert und dann rotiert und umgekehrt.

Wenn man die Matrizen R und [t]x miteinander multipliziert kommt eine Matrix von anderer Gestalt raus.
Außerdem wäre das Ergebnis der Multiplikation eines Punktes unterschiedlich (mit Octave geprüft).
Die Keuzproduktmatrix entspricht nicht einer Translation.
Außerdem ist es ein Unterschied, ob man erst transliert und dann rotiert und umgekehrt.

In welchem Koodinatensystem ist der Vektor t definiert?
Im Koordinatensystem der Kamera 1. Der Ursprung des Kamerakoordinatensystems liegt im optischen Zentrum der Kamera. Der Urspung des Weltkoordinatensystems wird meistens zur Vereinfachung in den Ursprung des Kamerakoordinatensystems der Kamera 1 gelegt.
Und warum ist das dann t und nicht -t, und in welchem Koordinatensystem wird dann rotiert?
Wir gehen stehts vom 1. Kamerasystem aus (in allen Abbildungen und Erklärungen) .. dem linken Kamerassystem. Der Ursprung dieses Kamerasystems liegt im Projektionszentrum 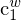 der ersten Kamera. Meisten legt man dort zur Vereinfachung auch den Urspung des Weltkoordinatensystems fest.
der ersten Kamera. Meisten legt man dort zur Vereinfachung auch den Urspung des Weltkoordinatensystems fest.
Ziel: Wir wollen den Sehstrahl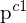 im 1. KKS auf
im 1. KKS auf 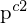 des 2.KKS im 1. KKS transformieren. Sämtliche Transformationen laufen praktisch also im 1.KKS ab und somit auch die Rotation.
des 2.KKS im 1. KKS transformieren. Sämtliche Transformationen laufen praktisch also im 1.KKS ab und somit auch die Rotation.
Wir wollen ja genau die unterschiedlichen Positionen im Bezug zu einem KKS.
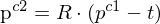
Wir translieren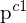 zunächst um
zunächst um 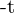 im 1.KKS. Dann wird er im 1.KKS mit
im 1.KKS. Dann wird er im 1.KKS mit 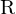 rotiert und befindet sich dann im 1.KKS an der Stelle von
rotiert und befindet sich dann im 1.KKS an der Stelle von 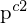 im 2.KKS.
im 2.KKS.
(Anmerkung: Denke an Erklärung von Fabi)
ToDo: gute Grafik erstellen
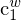 der ersten Kamera. Meisten legt man dort zur Vereinfachung auch den Urspung des Weltkoordinatensystems fest.
der ersten Kamera. Meisten legt man dort zur Vereinfachung auch den Urspung des Weltkoordinatensystems fest.Ziel: Wir wollen den Sehstrahl
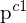 im 1. KKS auf
im 1. KKS auf 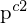 des 2.KKS im 1. KKS transformieren. Sämtliche Transformationen laufen praktisch also im 1.KKS ab und somit auch die Rotation.
des 2.KKS im 1. KKS transformieren. Sämtliche Transformationen laufen praktisch also im 1.KKS ab und somit auch die Rotation.Wir wollen ja genau die unterschiedlichen Positionen im Bezug zu einem KKS.
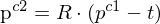
Wir translieren
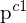 zunächst um
zunächst um 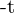 im 1.KKS. Dann wird er im 1.KKS mit
im 1.KKS. Dann wird er im 1.KKS mit 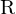 rotiert und befindet sich dann im 1.KKS an der Stelle von
rotiert und befindet sich dann im 1.KKS an der Stelle von 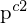 im 2.KKS.
im 2.KKS. (Anmerkung: Denke an Erklärung von Fabi)
ToDo: gute Grafik erstellen
Warum ist denn die Matrix mit zweimal der Brennweite und einer 1 auf der Diagonalen eine Projektionsmatrix?
Durch die Projektionsmatrix und schließlich die Homogenisierung verlieren wir die Tiefeninformation...wir "projezieren" den 3D-Punkt auf eine 2D-Ebene.
Die 1 stellt sicher, dass wir durch die Z-Koordinate (Tiefe) im Homogenisierungsschritt teilen und somit die korrekte Projektion erfüllt wird.
Als Erinnerung:

Als Erinnerung:
Wir teilen durch die Z-Koordinate, damit weiter entfernte Objekte kleiner abgebildet werden (größerer Wert Z unter Bruch => kleinerer Wert für x und y)
Die 1 stellt sicher, dass wir durch die Z-Koordinate (Tiefe) im Homogenisierungsschritt teilen und somit die korrekte Projektion erfüllt wird.
Als Erinnerung:

Als Erinnerung:
Wir teilen durch die Z-Koordinate, damit weiter entfernte Objekte kleiner abgebildet werden (größerer Wert Z unter Bruch => kleinerer Wert für x und y)
Wenn man die K-Matrix und die Projektionsmatrix aus der Epipolarbedingungsherleitung zusammen nimmt und mit der Pipeline in der Computergrafik vergleicht - können Sie mir sagen ob, und wenn ja, welcher Matrix der OpenGL-Pipeline das entspricht?
Da die Projektion durch F=1 "wegfällt" bzw. keinen Änderung verursacht (Identitästmatrix). Letztendlich bleibt die K-Matrix, die von Bildkoordinaten in Pixelkoordinaten abbildet, was in OpenGL der Viewport-Transormation entspricht. Die Viewport-Transofrmation ist aber eiegtnlich nicht Teil der OpenGL-Pipeline(also keine weitere Matrix), sondern geschieht expliziet durch:
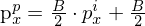
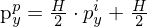
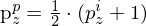
als Matrix wäre das:

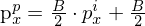
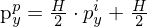
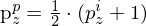
als Matrix wäre das:

Worum ging es bei der Veranstaltung CV-Integration? Was wurde behandelt?
Ziel: Gemeinsame Grundlagen von BV und CG sowie gemeinsame aktuelle Forschungsgebiete vorstellen.
Müller (CG):
Paulus(BV):
Müller (CG):
- Bildentstehung (wichtig bei markerlosem Tracking BV+CG)
- Photometrie (Messverfahren im sichtbaren Licht (math. Erklärungen), Wirkung auf Visuelles Empfängersystem)
- Materialbeschreibung (Licht-Materie-Wechselwirkung,BRDF)
- Licht und Farbe (Photometrische und colormetrische Konsistenz, Reflexion, Normierung)
- HDR und Tone-Mapping (RGB-Werte außerhalb der durch das Display darstellbaren Bereiches)
Paulus(BV):
- CCD-Eigenschaften,Kamera-Eigenschaften
- Methoden zur Erstellung und Vermessung von Licht (Abtastung)
- 3D-Rekonstruktion (für Modellbasierte Analyse)
- 3D-Modellierung (für Modellbasierte Analyse)
- Projektionsmodelle
Welche Inhalte wurde in Softwareergonomie II behandelt? Worum ging es in SEII?
- Ziele der Software-Ergonomie im Anwendungskontext
- Dynamische Elemente der Mensch-Maschine-Interaktion
- Subsiduäre Elemente der Mensch-Maschine-Interaktion
-Anwendungen (nach der Gestaltung)
- Integration von Ergonomie und Design
- Effektivität
- Effizienz
- Zufriedenheit
- Dynamische Elemente der Mensch-Maschine-Interaktion
- Dialogkriterien
- Subsiduäre Elemente der Mensch-Maschine-Interaktion
- Benutzerführung
- Hilfestellungen
-Anwendungen (nach der Gestaltung)
- Lernen mit neuen Medien (WebCT,...)
- Nomadische Informationssysteme (PDA,Handy (UMTS),...)
- Informationsvisualisierung (Newsmap(Nachrichtenbrowser(Zusammenhänge)))
- Integration von Ergonomie und Design
Flashcard set info:
Author: CoboCards-User
Main topic: Rechnsersehen
Topic: Epipolargeometrie
Published: 05.11.2010
Card tags:
All cards (53)
no tags





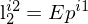
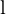 ist ein Komponentenvektor der Form
ist ein Komponentenvektor der Form  . Diese Notation passt zur homogenen 2D-Geradengleichung ax + by + c = 0, wodurch eine Linie eindeutig durch die Parameter a,b, c festgelegt werden kann.
. Diese Notation passt zur homogenen 2D-Geradengleichung ax + by + c = 0, wodurch eine Linie eindeutig durch die Parameter a,b, c festgelegt werden kann.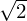 ist.
ist.
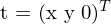 ist?
ist?